A. -12
B. 4
C. -4
D. 12
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
Ta có hàm số liên tục trên đoạn .
Vậy giá trị nhỏ nhất của hàm số trên đoạn là -12
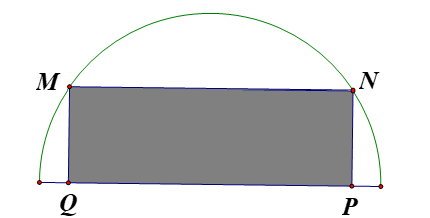
Từ một miếng tôn hình bán nguyệt có bán kínhR=4 , người ta muốn cắt một hình chữ nhật (xem hình vẽ) có diện tích lớn nhất. Diện tích lớn nhất có thể của miếng tôn hình chữ nhật bằng
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có 1 tiệm cận đứng.
Cho hàm số (m là tham số thực). Tất cả các giá trị thực của tham số m để hàm số nghịch biến trên từng khoảng xác định của nó là
Cho hình chóp đều SABC có tất cả các cạnh bằng a. Mặt phẳng (P) song song với mặt đáy (ABC) và cắt các cạnh bên SA, SB, SC lần lượt tại các điểm M,N,P. Biết mặt phẳng (P) chia khối chóp đã cho thành hai phần có thể tích bằng nhau. Chu vi tam giác MNP bằng
Cho hình hộp chữ nhật ABCDA'B'C'D' có AB= x, AD=3 góc giữa đường thẳng A'C và mặt phẳng ( ABB'A') bằng . Tìm giá trị lớn nhất của thể tích khối hộp chữ nhật.
Cho hình chóp SABC, đáy ABC đều canh 2a. cạnh bên SA vuông góc với mặt đáy. Góc giữa SB và ( ABC) là 60. Thể tích SABC là
Cho lăng trụ tam giác đều ABCA'B'C có cạnh đáy bằng 2a, góc giữa ( A'BC) và mặt phẳng đáy bằng 60. Thể tích khối lăng trụ bằng
Cho hàm số (m là tham số thực). Tất cả các giá trị thực của tham số m để hàm số đồng biến trên R là
Cho lăng trụ ABCA'B'C' có đáy là tam giác đều cạnh 2. Hình chiếu vuông góc của A' lên mặt phẳng ( ABC) trùng với trung điểm H của BC. Góc tạo bởi cạnh bên AA'với mặt đáy bằng 45. Thể tích của khối lăng trụ đã cho bằng