Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.
 Giải bởi Vietjack
Giải bởi Vietjack
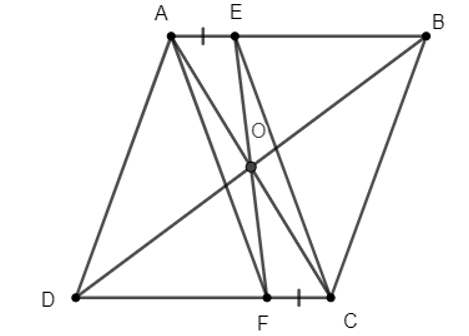
Vì ABCD là hình bình hành
AB//CD hay AE//CF.
Lại có: AE = CF (gt),
Suy ra AECF là hình bình hành.
AC, EF cắt nhau tại trung điểm mỗi đường.
Hay O ∈ AC; O ∈ CF (1).
Mà AC và BD cũng cắt nhau tại trung điểm mỗi đường ( do ABCD là hình bình hành).
O ∈ AC; O ∈ BD (2).
Từ (1) và (2) suy ra ba đường thẳng AC, BD, EF đồng quy (đpcm).
Một lớp có 45 học sinh. Mỗi em đều đăng ký chơi ít nhất một trong hai môn: bóng đá và bóng chuyền. Có 35 em đăng ký môn bóng đá, 15 em đăng ký môn bóng chuyền. Hỏi có bao nhiêu em đăng ký cả hai môn bóng đá và bóng chuyền?
Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9, có thể lập được bao nhiêu số tự nhiên có 4 chữ số nhỏ hơn 2811?
Trong không gian Oxyz, phương trình mặt phẳng (P) chứa trục Ox và vuông góc với mặt phẳng (Q): 3x + y – 2z – 5 = 0 là:
Cho bất phương trình bậc nhất hai ẩn x + 2y ≥ 0.
a) Hãy chỉ ra ít nhất hai nghiệm của bất phương trình trên.
b) Với y = 0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?
Cho tam giác ABC nhọn (AB < AC). Đường tròn tâm O, đường kính BC lần lượt cắt AB, AC tại M và N; BN và CM giao nhau tại H, AH cắt BC tại K.
a) Chứng minh: .
b) Chứng minh: AM.AB = AN.AC
c) Chứng minh: MH là phân giác góc NMK.
d) MN và BC cắt nhau tại S. Chứng minh: SB.SC = SK. SO
Phân tích đa thức thành nhân tử: A = (x + 2)(x + 3)(x + 4)(x + 5) − 24
Chứng minh P(n) = n4 – 14n3 + 71n2 – 154n + 120 chia hết cho 24 với mọi số tự nhiên n khác 0.