Cho đường tròn tâm O và BC là dây cung không đi qua tâm. Trên tia đối của tia BC lấy điểm M sao cho M không trùng với B. Đường thẳng đi qua M cắt đường tròn (O) đã cho tại N và P (N nằm giữa M và P) sao cho O nằm trong PMC. Gọi A là điểm chính giữa của cung nhỏ NP. Các dây AB và AC lần lượt cắt NP tại D và E.
a) Chứng minh tứ giác BDEC nội tiếp.
 Giải bởi Vietjack
Giải bởi Vietjack
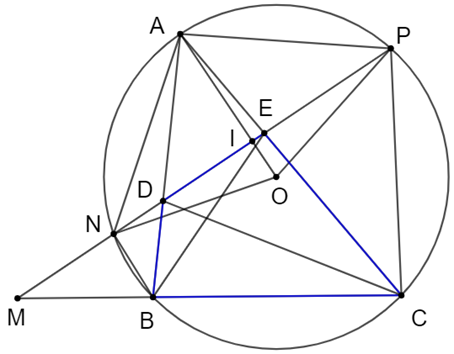
a) Gọi I là giao điểm của OA và NP
Ta có độ dài cung AN bằng độ dài cung AP nên suy ra AN = AP
Và ON = OP = R.
=> OA là đường trung trực của đoạn thẳng NP
=> OA NP tại I
=>
Hay
Lại có: OA = OB => ∆OAB cân tại O.
Suy ra
Mà (Hai góc đối đỉnh)
Đường tròn (O) có: là góc nội tiếp chắn cung AB và là góc ở tâm chắn cung AB nên suy ra:
Hay
Tứ giác BNDC có
Suy ra BNDC là tứ giác nội tiếp.
b) Nếu đường thẳng d nằm ngoài tam giác ABC và G' là hình chiếu của G trên d thì các độ dài AA', BB', CC', GG' có liên hệ gì?
Cho đường tròn (O), đường kính AB, vẽ các tiếp tuyến Ax, By. Từ M trên đường tròn (M khác A,B) vẽ tiếp tuyến thứ ba nó cắt Ax ở C cắt By ở D. Gọi N là giao điểm của BC và AD.
a) CMR:
Cho nửa đường tròn (O), đường kính AB; Ax là tiếp tuyến của nửa đường tròn. Trên nửa đường tròn lấy điểm D (D khác A, B). Tiếp tuyến tại D của (O) cắt Ax ở S.
a) Chứng minh SO // BD.
Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường tròn (O) lấy một điểm E bất kì (E khác A, B). Tiếp tuyến tại E của đường tròn (O) cắt Ax, By lần lượt tại C, D.
a) CM: CD = AC + BD.
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Đường thẳng d thay đổi đi qua M cắt đường tròn tại 2 điểm phân biệt C và D (C nằm giữa M và D)
a) Chứng minh tứ giác AMBO nội tiếp
Cho tam giác ABC có A(−5; 6), B(−4; −1), C(4; 3). Tìm tọa độ trung điểm I của AC. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
Tổng của hai số là 19,1. Nếu giảm số hạng thứ nhất đi 4 lần và giữ nguyên số hạng thứ hai thì được tổng mới là 7,4. Tìm hai số đó.
Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.
a) Chứng minh M đối xứng với N qua O.
Cho tam giác ABC, trọng tâm G. Vẽ đường thẳng d đi qua G cắt các đoạn thẳng AB, AC. Goi A', B', C' thứ tự là hình chiếu của A, B, C trên d. Tìm liên hệ giữa các độ dài AA', BB', CC'.
Một liên đội thiếu niên khi xếp hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người. Tính số đội viên của liên đội biết rằng số đội viên khoảng từ 100 đến 150?
Cho tứ giác ABCD có
a) CMR: 4 điểm A, B, C, D cùng thuộc một đường tròn, tìm tâm đường tròn đó.
c) Tìm m để đường thẳng (d) tạo với 2 trục tọa độ một tam giác có diện tích bằng 3
Một tổ công nhân có 8 người dự định làm xong 1 sân bóng chuyền trong 6 ngày nhưng sau đó người ta quyết định là xong sân bóng sớm hơn 2 ngày. Hỏi như vậy phải bổ sung thêm bao nhiêu công nhân?