- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 7)
-
12952 lượt thi
-
121 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số và . Gọi A là giao điểm của d1 và d2, B và C lần lượt là giao của d1 và d2, với Ox. Tìm m nhỏ nhất để tam giác ABC có diện tích nhỏ nhất.
 Xem đáp án
Xem đáp án
• Vì A là giao điểm của d1 và d2 nên hoành độ giao điểm của A là nghiệm của phương trình nên:
Khi đó tọa độ của điểm A là A(0; 3).
• Vì B là giao điểm của d1 và Ox nên hoành độ giao điểm của B là nghiệm của phương trình nên:
mx + 3 = 0
Khi đó, tọa độ của điểm B là
• Vì C là giao điểm của d2 và Ox nên hoành độ giao điểm của C là nghiệm của phương trình nên:
Khi đó, tọa độ của điểm C là C(3m; 0).
Hệ số góc của d1 là m và hệ số góc của d2 là có nên hai đường thẳng d1 và d2 vuông góc với nhau tại A.
Khi đó, tam giác ABC là tam giác vuông tại A và có diện tích là
Ta có:
Áp dụng BĐT Cô-si vào 2 số dương và ta có:
Dấu “=” xảy ra khi và chỉ khi
Vậy giá trị m nhỏ nhất là m = −1 thì diện tích tam giác ABC đạt giá trị nhỏ nhất là 9.
Câu 2:
Cho hai đường thẳng và
Gọi A và B theo thứ tự giao điểm của (D1) và (D2) với các trục hoành, C là giao điểm của hai đường thẳng đó (đơn vị trên các trục tọa độ là centimet).
Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án

• Vì A là giao điểm của (D1) với trục hoành nên hoành độ giao điểm của A là nghiệm của phương trình:
Khi đó, tọa độ của điểm A là A(– 4, 0).
=> OA = 8 (cm)
• Vì B là giao điểm của (D2) với trục hoành nên hoành độ giao điểm của A là nghiệm của phương trình:
– x + 2 = 0 Û x = 2
Khi đó, tọa độ của điểm B là B(2, 0).
=> OB = 2 (cm)
• Vì C là giao điểm của hai đường thẳng (D1) và (D2) nên hoành độ giao điểm của C là nghiệm của phương trình:
Khi đó, tọa độ của điểm C là C(0; 2).
=> OC = 2 (cm)
Xét khẳng định A.
Do đó
Vậy khẳng định A đúng.
Xét khẳng định B.
Ta có AB = 6 (cm).
Theo định lí Py-ta-go, ta có:
AC2 = OA2 + OC2 = 42 + 22 = 20
Theo định lí Py-ta-go, ta có:
BC2 = OB2 + OC2 = 22 + 22 = 8
Chu vi tam giác ABC là:
P∆ABC= AB + AC + BC = 6 + 4,47 + 2,83 = 13,3 (cm).
Vậy khẳng định B sai.
Xét khẳng định C.
Diện tích tam giác ABC là:
Vậy khẳng định C đúng.
Câu 4:
Tìm m để hàm số xác định trên khoảng (0; 1)?
 Xem đáp án
Xem đáp án
Điều kiện:
=> TXĐ:
Để hàm số xác định trên khoảng (0; 1) thì (0; 1) là con của
Vậy
Câu 5:
Tìm tất cả các giá trị thực của tham số m để hàm số xác định trên khoảng (−1; 3).
 Xem đáp án
Xem đáp án
Chọn A
Điều kiện:
=> TXĐ:
Để hàm số xác định trên khoảng (−1; 3) thì (−1; 3) là con của
Vậy không có giá trị của m nào thỏa mãn.
Câu 6:
 Xem đáp án
Xem đáp án
x3 − 3x + 2 = 0
<=> x3 − x − 2x + 2 = 0
<=> x(x2 − 1) − 2(x − 1) = 0
<=> x(x − 1)(x + 1) − 2(x − 1) = 0
<=> (x − 1)(x2 + x − 2) = 0
<=> (x − 1)[x2 − x + 2x − 2] = 0
<=> (x − 1)[x(x − 1) + 2(x − 1)] = 0
<=> (x − 1)2(x + 2) = 0
Vậy nghiệm của phương trình là x = 1 và x = −2.
Câu 7:
Cho hình bình hành ABCD, gọi O là giao điểm của AC và BD. Các khẳng định sau đúng hay sai?
a)
b)
c)
 Xem đáp án
Xem đáp án
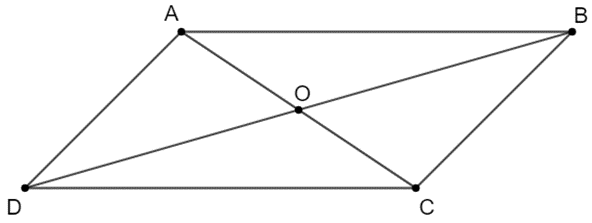
+ Do ABCD là hình bình hành nên
Do đó:
Vậy khẳng định a) đúng.
+ Ta có:
Mà (Do ABCD là hình bình hành)
Do đó:
Vậy khẳng định b) sai.
+ Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên O là trung điểm của AC và BD.
Khi đó ta có:
Do đó:
Suy ra:
Vậy khẳng định c) sai.
Câu 8:
Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Qua O vẽ đường thẳng a cắt AD, BC lần lượt tại E, F. Qua O vẽ đường thẳng b cắt AB và CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành.
 Xem đáp án
Xem đáp án
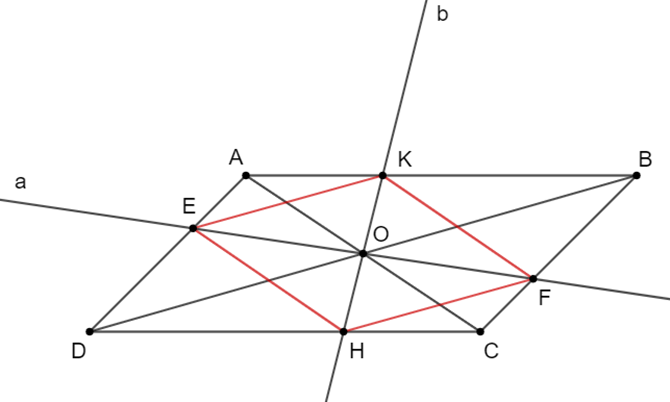
Do ABCD là hình bình hành nên ta có:
+) (Hai góc ở vị trí so le trong).
+) (Hai góc ở vị trí so le trong).
Xét ∆KOB và ∆HOD có:
(cmt)
OB = OD (gt)
(Hai góc đối đỉnh)
=> ∆KOB = ∆HOD (g.c.g)
=> OK = OH (Hai cạnh tương ứng bằng nhau) (1)
Xét ∆EOA và FOC có:
(cmt)
OA = OC (gt)
(Hai góc đối đỉnh)
=> ∆EOA = ∆FOC (g.c.g)
=> OE = OF (Hai cạnh tương ứng bằng nhau) (2)
Từ (1) và (2) ta có tứ giác EKFH có hai cặp cạnh đối thỏa mãn OK = OH và OE = OF.
Suy ra EKFH là hình bình hành.
Câu 9:
Cho hai tập hợp E = (2;5] và F = [2m - 3; 2m + 2]. Tìm tất cả các giá trị của tham số m để E hợp F là một đoạn có độ dài bằng 5.
 Xem đáp án
Xem đáp án
Do (2m + 2) − (2m − 3) = 5 nên độ dài của tập F bằng 5.
Để là một đoạn có độ dài bằng 5 khi và chỉ khi C = F.
Vậy các giá trị của tham số m thỏa mãn yêu cầu bài toán là
Câu 10:
Tìm m để đa thức: A(x) = x3 − 3x2 + 5x + m chia hết cho đa thức B(x) = x − 2
 Xem đáp án
Xem đáp án
Ta có A(x) = x3 − 3x2 + 5x + m
= (x3 − 2x2) − (x2 − 2x) + (3x − 6) + m + 6
= x2(x − 2) − x(x − 2) + 3(x − 2) + m + 6
= (x2 − x + 3)(x − 2)
Thực hiện phép chia A(x) = x3 − 3x2 + 5x + m cho đa thức B(x) = x − 2.
Ta được thương là x2 − x + 3 và số dư là m + 6.
Để A(x) chia hết cho B(x) thì số dư của phép chia phải bằng 0.
Khi đó m + 6 = 0
<=> m = − 6
Vậy m = − 6 là giá trị m cần tìm.
Câu 11:
Tính độ dài MN trên hình vẽ.
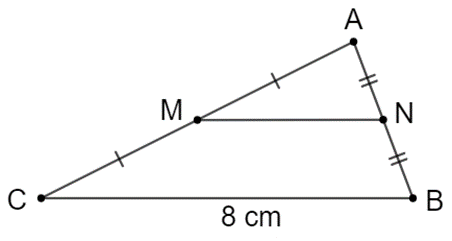
 Xem đáp án
Xem đáp án
Xét tam giác ABC có:
M là trung điểm của đoạn thẳng AB (AM = MC)
N là trung điểm của đoạn thẳng AB (AN = NB)
=> MN là đường trung bình của tam giác ABC.
Câu 12:
Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.
a) Chứng minh M đối xứng với N qua O.
 Xem đáp án
Xem đáp án
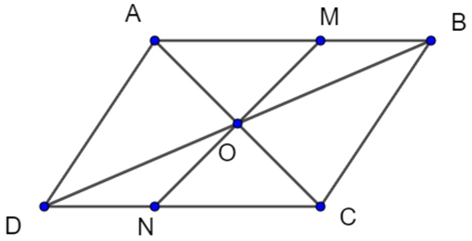
a) ABCD là hình bình hành
; O là trung điểm của AC
(so le trong)
Xét ΔMAO và ΔNCO có:
(cmt)
OA= OC (cmt)
(đối đỉnh)
=> ΔMAO = ΔNCO (g.c.g)
=> OM = ON
=> O là trung điểm của MN
=> M đối xứng với N qua O.
Câu 13:
b) Chứng tỏ rằng tứ giác AMCN là hình bình hành.
 Xem đáp án
Xem đáp án
b) ΔMAO = ΔNCO (cmt) => AM = CN
Xét tứ giác AMCN có:
AM // CN và AM = CN
Vậy AMCN là hình bình hành
Câu 14:
Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Qua O vẽ đường thẳng a cắt AD, BC lần lượt tại E, F. Qua O vẽ đường thẳng b cắt AB và CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành.
 Xem đáp án
Xem đáp án
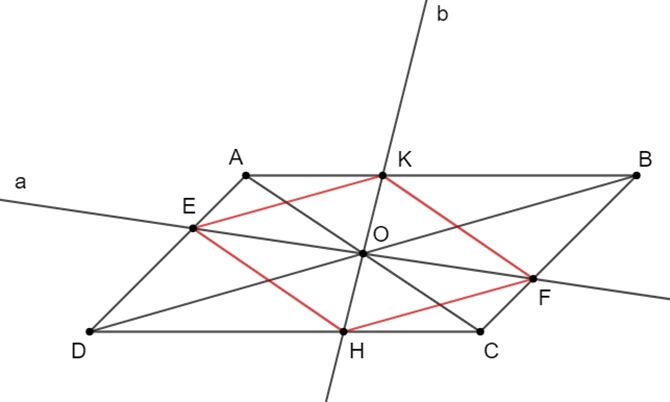
Do ABCD là hình bình hành nên ta có:
+) (Hai góc ở vị trí so le trong).
+) (Hai góc ở vị trí so le trong).
Xét ∆KOB và ∆HOD có:
(cmt)
OB = OD (gt)
(Hai góc đối đỉnh)
=> ∆KOB = ∆HOD (g.c.g)
=> OK = OH (Hai cạnh tương ứng bằng nhau) (1)
Xét ∆EOA và ∆FOC có:
(cmt)
OA = OC (gt)
(Hai góc đối đỉnh)
=> ∆EOA = ∆FOC (g.c.g)
=> OE = OF (Hai cạnh tương ứng bằng nhau) (2)
Từ (1) và (2) ta có tứ giác EKFH có hai cặp cạnh đối thỏa mãn OK = OH và OE = OF.
Suy ra EKFH là hình bình hành.
Câu 15:
Tìm tập hợp X sao cho
 Xem đáp án
Xem đáp án
Tập X có thể xảy ra những trường hợp sau:
X = {a; b};
Hoặc X = {a; b; c};
Hoặc X = {a; b; d};
Hoặc X = {a; b; c; d}.
Câu 16:
 Xem đáp án
Xem đáp án
a) Tập X có thể xảy ra những trường hợp sau:
X = {a; b};
Hoặc: X = {a; b; c}; X = {a; b; d}; X = {a; b; e};
Hoặc: X = {a; b; c; d}; X = {a; b; c; e}; X = {a; b; d; e};
Hoặc: X = {a; b; c; d; e}.
Câu 17:
b) Cho A = {1; 2}, B = {1; 2; 3; 4; 5}. Xác định các tập hợp X sao cho
 Xem đáp án
Xem đáp án
b) Để thì tập X có thể xảy ra những trường hợp sau:
X = {3; 4; 5};
Hoặc: X = {1; 3; 4; 5}; X = {2; 3; 4; 5};
Hoặc: X = {1; 2; 3; 4; 5}.
Câu 18:
 Xem đáp án
Xem đáp án
a) Để đường thẳng y = (m + 2)x + m song song với đường thẳng y = 3x − 2 thì:
Vậy m = 1 là giá trị của m thỏa mãn yêu cầu bài toán.
Câu 19:
 Xem đáp án
Xem đáp án
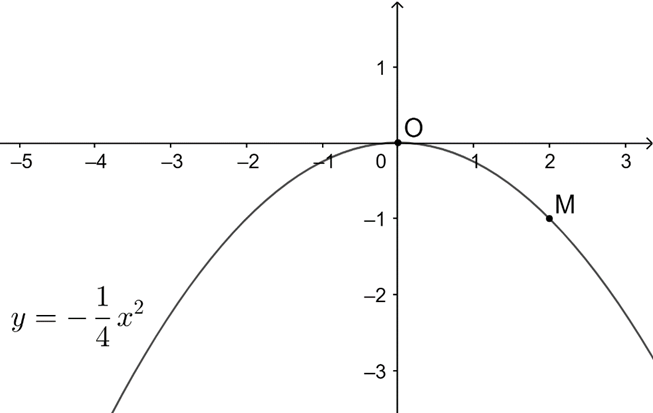
b) Đồ thị của hàm số
• Với x = 0 => y = 0 nên đồ thị hàm số đi qua O(0; 0).
• Với x = 2 nên đồ thị hàm số đi qua điểm M(2; −1).
Ta có đồ thị hàm số như sau:
Câu 20:
Tìm m, n để đường thẳng y = mx + n song song với đường thẳng y = 3x + 2 và cắt trục hoành tại điểm có hoành độ là 2.
 Xem đáp án
Xem đáp án
Để y = mx + n song song với y = 3x + 2 thì
Phương trình đường thẳng có dạng: y = 3x + n (n ≠ 2).
Do đường thẳng cắt trục hoành tại điểm có hoành độ bằng 2 nên 0 = 3.2 + n => n = −6
Vậy m = 3 và n = −6.
Câu 21:
 Xem đáp án
Xem đáp án
• Thay x = 2, y = −1 vào phương trình 2x + y = 3, ta được:
Do đó (2; −1) là nghiệm của phương trình 2x + y = 3.
• Thay x = 2, y = −1 vào phương trình x – 2y = 4, ta được:
Do đó (2; −1) là nghiệm của phương trình x – 2y = 4.
Vậy cặp số (x; y) = (2; −1) vừa là nghiệm của phương trình thứ nhất, vừa là nghiệm của phương trình thứ hai.
Câu 22:
Cho phương tình 3x − 2y = 6. (1)
a) Viết công thức nghiệm tổng quát của phương trình (1);
 Xem đáp án
Xem đáp án
a) Xét 3x − 2y = 6. (1)
Suy ra
Cho x một giá trị t tùy ý ta tính được giá trị tương ứng của y.
Ta được công thức nghiệm tổng quát của phương trình (1) là:
Câu 23:
b) Tìm nghiệm nguyên của phương trình (1).
 Xem đáp án
Xem đáp án
b) Ta có
Đặt suy ra x = 2t + 6.
Khi đó, nghiệm nguyên của phương trình (1) là:
Cho t một giá trị nguyên nào đó ta được một nghiệm nguyên của phương trình (1).
Chẳng hạn, với t = 1 thì
Với t = 2 thìCâu 24:
1 tấn bằng bao nhiêu tạ? tấn bằng bao nhiêu kg?
 Xem đáp án
Xem đáp án
1 tấn = 10 tạ = 1 000 kg.
Vậy (tấn) .
Câu 26:
Cho tam giác ABC, trọng tâm G. Vẽ đường thẳng d đi qua G cắt các đoạn thẳng AB, AC. Goi A', B', C' thứ tự là hình chiếu của A, B, C trên d. Tìm liên hệ giữa các độ dài AA', BB', CC'.
 Xem đáp án
Xem đáp án
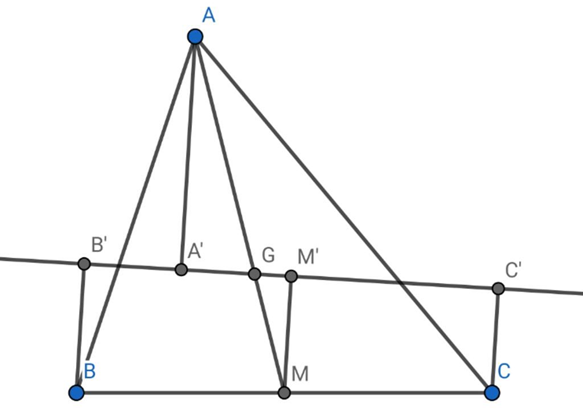
Gọi M là trung điểm của BC
M' là hình chiếu của M lên d
=> MM' // BB' // CC'
=> MM' là đường trung bình của hình thang vuông BB'C'C
Xét ∆AA'G và ∆MM'G có:
(so le trong)
Do đó ∆AA'G ᔕ ∆MM'G (g.g)
Áp dụng tính chất của trọng tâm, ta có:
Do đó:
Vậy AA' = BB' + CC'.
Câu 27:
Cho tam giác ABC, trọng tâm G.
a) Vẽ đường thẳng d qua G, cắt các đoạn thẳng AB, AC. Gọi A', B', C' là hình chiếu của A, B, C trên d. Tìm liên hệ giữa các độ dài AA', BB', CC'
 Xem đáp án
Xem đáp án
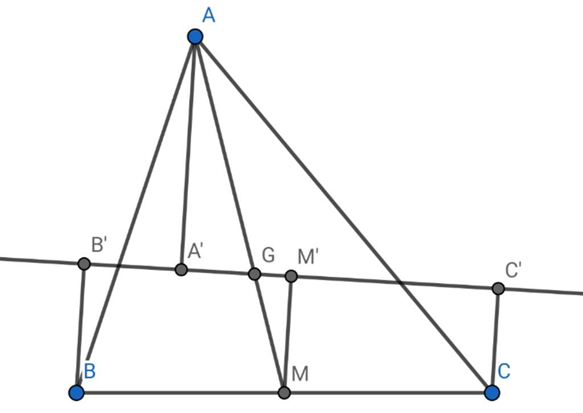
Gọi M là trung điểm của BC
M' là hình chiếu của M lên d
=> MM' // BB' // CC'
=> MM' là đường trung bình của hình thang vuông BB'C'C
Xét ∆AA'G và ∆MM'G có:
(so le trong)
Do đó ∆AA'G ᔕ ∆MM'G (g.g)
Áp dụng tính chất của trọng tâm, ta có:
Do đó:
Vậy AA' = BB' + CC'.
Câu 28:
b) Nếu đường thẳng d nằm ngoài tam giác ABC và G' là hình chiếu của G trên d thì các độ dài AA', BB', CC', GG' có liên hệ gì?
 Xem đáp án
Xem đáp án
b)
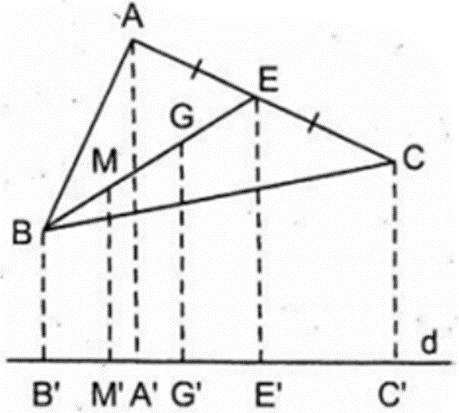
Gọi BE là đường trung tuyến của của AC, M là trung điểm của BG.
Vẽ AA', BB', CC', II', MM' vuông góc với d.
Ta có: G là trọng tâm của tam giác ABC nên suy ra
Suy ra G là trung điểm của ME
M', G', E' là hình chiếu của M, G, E lên d
=> MM' // GG' // EE'
=> GG' là đường trung bình của hình thang vuông MM'E'E
Chứng minh tương tự ta có MM' là đường trung bình của hình thang vuông BB'G'G.
Và EE' là đường trung bình của hình thang vuông AA'C'C.
Khi đó ta có:
MM' + EE' = 2GG'
=> 2MM' + 2EE' = 4GG'
=> BB' + GG' + AA' + CC' = 4GG'
=> AA' + BB' + CC' = 3GG'
Câu 29:
Một tổ công nhân có 8 người dự định làm xong 1 sân bóng chuyền trong 6 ngày nhưng sau đó người ta quyết định là xong sân bóng sớm hơn 2 ngày. Hỏi như vậy phải bổ sung thêm bao nhiêu công nhân?
 Xem đáp án
Xem đáp án
1 người làm xong sân trong số ngày là:
8 × 6 = 48 (ngày)
Sớm hơn 2 ngày thì làm xong sau:
6 − 2 = 4 (ngày)
Số công nhân để làm xong trong 4 ngày là:
48 : 4 = 12 (công nhân)
Vậy cần bổ sung số công nhân là:
12 − 8 = 4 (công nhân)
Đáp số: 4 công nhân.
Câu 30:
Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và SC. Tìm giao tuyến của (SMN) và (SBD).
 Xem đáp án
Xem đáp án
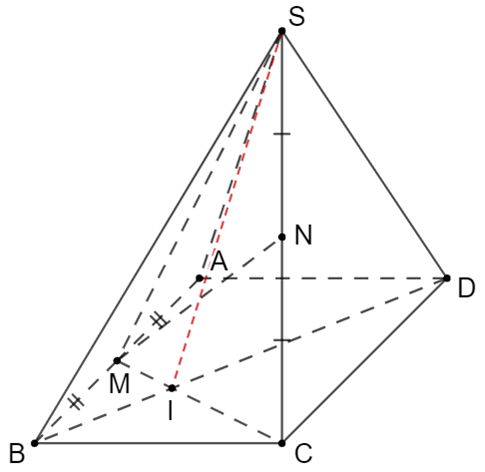
Ta có: và SM cắt SC tại S
Gọi I là giao điểm của BD và MC
Vì nên
Ta thấy: (SBD) và (SMC) có điểm chung là S
=> SI là giao tuyến của (SBD) và (SMC)
=> SI giao tuyến của (SBD) và (SMN).
Câu 31:
a) Tìm giao tuyến của hai mặt phẳng (ABN) và (SCD).
 Xem đáp án
Xem đáp án
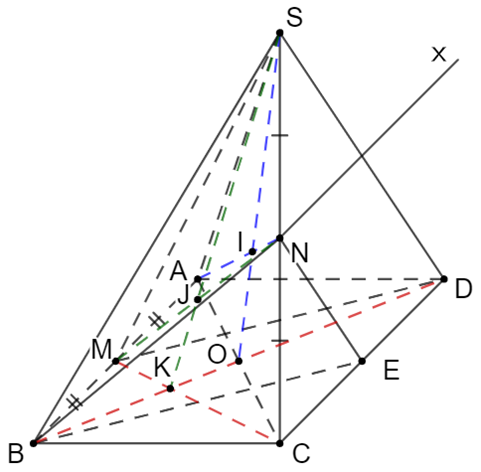
a) N là điểm chung của (ABN) và (SCD).
Mà AB // CD => (ABN) ∩ (SCD) = Nx // CD // AB.
Câu 32:
b) Chứng minh đường thẳng BN song song với mặt phẳng (SDM).
 Xem đáp án
Xem đáp án
b) Gọi E là trung điểm của CD
Xét tam giác CSD có
Áp dụng định lý Ta-lét đảo suy ra: EN // SD (1)
Ta thấy BM // DE và BM = DE suy ra DMBE là hình bình hành.
=> BE // DM (2)
Từ (1) và (2) => (BNE) // (SDM)
=> BN // (SDM)
Câu 33:
 Xem đáp án
Xem đáp án
c) Gọi O là tâm của hình bình hành ABCD.
Ta có O (SBD) => SO (SBD)
=> I = SO AN là điểm cần tìm.
Gọi K là giao điểm của MC và BD
=> K (SBD) => SK (SBD)
=> J = SK MN là điểm cần tìm.
Câu 34:
d) Tính tỉ số
 Xem đáp án
Xem đáp án
d) Xét tam giác SAC có I là giao điểm của hai đường trung tuyến là SO và AN nên I là trọng tâm của tam giác SAC
Do MB // CD nên theo định lí Ta-lét ta có:
Xét tam giác MSC có:
Xét tam giác BNA có:
Câu 35:
Cho tam giác ABC có A(−5; 6), B(−4; −1), C(4; 3). Tìm tọa độ trung điểm I của AC. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
 Xem đáp án
Xem đáp án
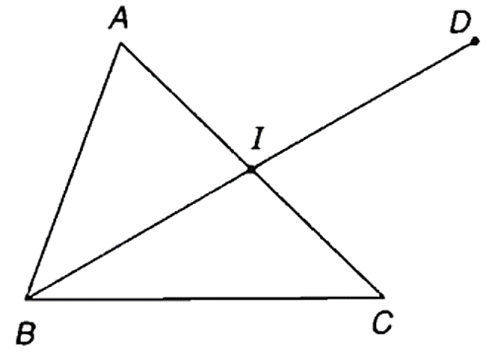
Gọi I là trung điểm của AC.
Để tứ giác ABCD là hình bình hành suy ra I là trung điểm của BD.
Do đó, ta có:
Vậy tọa độ đỉnh D là (3; 10).
Câu 36:
Cho tứ giác ABCD có
a) CMR: 4 điểm A, B, C, D cùng thuộc một đường tròn, tìm tâm đường tròn đó.
 Xem đáp án
Xem đáp án
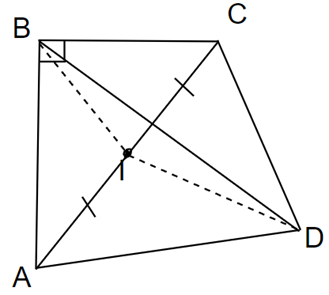
a) Gọi I là trung điểm của AC.
Xét tam giác vuông BAC có BI là đường trung tuyến
=> BI = IA = IC (1)
Xét tam giác vuông DAC có DI là đường trung tuyến
=> DI = IA = IC (2)
Từ (1) và (2) => IA = IB = IC = ID.
Vậy 4 điểm A, B, C, D cùng thuộc 1 đường tròn là đường tròn tâm I và bán kính là AI.
Câu 37:
b) So sánh độ dài AC và BD. Tứ giác ABCD cần thêm điều kiện gì thì AC = BD
 Xem đáp án
Xem đáp án
b) Xét tam giác BDI ta có: BI + ID > BD (theo bất đẳng thức tam giác).
Mà
Vậy AC > BD.
Để AC = BD thì BD cũng là đường kính của đường tròn ngoại tiếp tứ giác ABCD.
Khi đó ABCD là hình chữ nhật.
Câu 38:
Tìm hiệu của số lớn nhất có ba chữ số và số bé nhất có ba chữ số khác nhau
 Xem đáp án
Xem đáp án
Số lớn nhất có 3 chữ số là 999.
Số bé nhất có ba chữ số khác nhau là 102.
Suy ra hiệu của chúng là:
999 − 102 = 897.
Đáp số: 897.
Câu 39:
Tìm hiệu của số lớn nhất có ba chữ số khác nhau và số bé nhất có ba chữ số khác nhau
 Xem đáp án
Xem đáp án
Số lớn nhất có ba chữ số khác nhau: 987.
Số bé nhất có ba chữ số khác nhau: 102.
Hiệu của số lớn nhất có ba chữ số khác nhau và số bé nhất có ba chữ số khác nhau là: 987 − 102 = 885.
Đáp số: 885.
Câu 40:
Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên gồm 3 chữ số phân biệt.
 Xem đáp án
Xem đáp án
Chọn C
Gọi số tự nhiên thỏa mãn đề bài là
Có 5 cách chọn a.
Có 4 cách chọn b.
Có 3 cách chọn c.
Số số lập được là: 5.4.3 = 60.
Câu 41:
Từ các chữ số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên gồm 2 chữ số khác nhau?
 Xem đáp án
Xem đáp án
Chọn C
Mỗi số có 2 chữ số khác nhau được lập từ 5 chữ số là chỉnh hợp chập 2 của 5.
Câu 44:
c) Đặt P = A.B. Tìm giá trị nguyên của x để P < 1
 Xem đáp án
Xem đáp án
c) , với x ≥ 0; x ≠ 1.
Để
Do
=> 0 < x < 4.
Kết hợp ĐKXĐ Þ x Î (0; 4) \ {1}.
Câu 45:
Tính 155,7 : 45
 Xem đáp án
Xem đáp án
155,7 : 45 = 1 557 : 10 : 45 = 1 557 : 45 : 10
= 1 557 : 9 : 5 : 10 = 173 : 5 : 10
= 1730 : 10 : 5 : 10 = 1730 : 5 : 100
= 346 : 100 = 3,46.
Câu 46:
Đặt tính rồi tính 155,9 : 45
 Xem đáp án
Xem đáp án

Thử lại: 45 × 3,4 + 2,9 = 155,9
Vậy 155,9 : 45 = 3,4 (dư 2,9).
Câu 47:
Cho nửa đường tròn (O), đường kính AB; Ax là tiếp tuyến của nửa đường tròn. Trên nửa đường tròn lấy điểm D (D khác A, B). Tiếp tuyến tại D của (O) cắt Ax ở S.
a) Chứng minh SO // BD.
 Xem đáp án
Xem đáp án
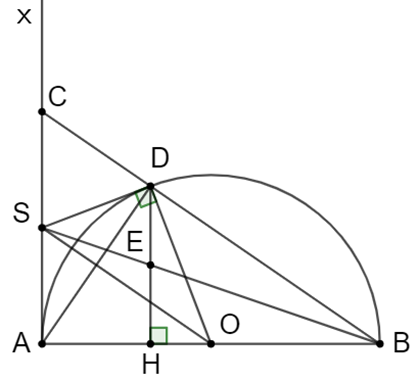
a) Ta có: SA và SD là hai tiếp tuyến của (O) và cắt nhau tại S => SA = SD.
Mà OA = OD (Bán kính của đường tròn (O)).
Khi đó SO là đường trung trực của đoạn thẳng AD => SO AD.
Tam giác ABD nội tiếp đường tròn (O) nên suy ra AD BD.
Vậy suy ra SO // BD (đpcm).
Câu 48:
b) BD cắt AS ở C. Chứng minh SA = SC.
 Xem đáp án
Xem đáp án
b) Xét ∆ABC có:
O là trung điểm của AB;
SO // BD (cmt).
Suy ra SO là đường trung bình của ∆ABC.
Do đó S là trung điểm của AC.
Vậy SA = SC (đpcm).
Câu 49:
c) Kẻ DH vuông góc với AB; DH cắt BS tại E. Chứng minh E là trung điểm của DH.
 Xem đáp án
Xem đáp án
c) Do AC AB và DH AB nên suy ra AC // DH
Xét ∆BSC có ED // SC. Theo định lý Ta-lét, ta có: (1)
Xét ∆BSA có EH // SA. Theo định lý Ta-lét, ta có: (2)
Từ (1) và (2)
Mà SC = SA => ED = EH.
Vậy E là trung điểm của DH.
Câu 50:
Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C khác A, B) vẽ tiếp tuyến CM cắt Ax tại M, hạ CH vuông góc với AB, MB cắt (O) tại Q và cắt CH tại N.
a) Chứng minh MA2 = MQ.MB Xem đáp án
Xem đáp án
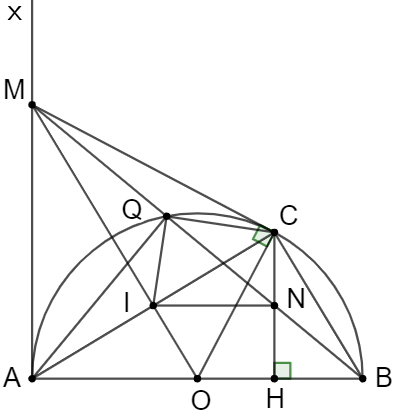
a) ∆AQB nội tiếp đường tròn (O)
(góc nội tiếp chắn nửa đường tròn).
=> AQ BM.
Tam giác ABM vuông tại A có AQ BM, ta áp dụng hệ thức lượng trong tam giác vuông suy ra: MA2 = MQ.MB (đpcm).
Câu 51:
 Xem đáp án
Xem đáp án
b) ∆ACB nội tiếp đường tròn (O)
(Góc nội tiếp chắn nửa đường tròn)
=> AC BC (1)
Ta có: OA = OC (Bán kính của đường tròn tâm O)
Và MA = MC (Hai tiếp tuyến MA, MC cắt nhau tại M)
=> MO là đường trung trực của đoạn thẳng AC
=> MO AC (2)
Từ (1) và (2) => BC // OM (Cùng vuông góc với AC)
(Hai góc ở vị trí so le trong)
Hay (3)
Mặt khác: (Hai góc nội tiếp đường tròn (O) cùng chắn cung QC) (4)
Từ (3) và (4)
Do M và A cùng nhìn QI cố định dưới hai góc bằng nhau nên tứ giác AIQM nội tiếp.
Câu 52:
c) Chứng minh: IN CH.
 Xem đáp án
Xem đáp án
c) Do tứ giác AIQM nội tiếp nên suy ra:
(Hai góc nội tiếp đường tròn cùng chắn cung AI) (5)
Ta có: (6)
Xét tam giác AIM vuông tại I có
Và
(Hai góc cùng phụ với ) (7)
Xét tam giác CAH vuông tại H có:
Hay (8)
Từ (5), (6), (7) và (8)
Do Q và C cùng nhìn IN cố định dưới hai góc bằng nhau nên tứ giác IQCN nội tiếp.
(Hai góc nội tiếp đường tròn cùng chắn cung CN) (*)
Mà (Hai góc nội tiếp đường tròn (O) cùng chắn cung CB) (**)
Từ (*) và (**) nên suy ra
=> IN // AH (Có hai góc ở vị trí đồng vị bằng nhau)
Mà AH CH nên suy ra IN CH.
Câu 53:
Cho tam giác ABC cân ở A. Gọi I là giao điểm các đường phân giác.
a) Xác định vị trí tương đối của đường thẳng AC với đường tròn (O) ngoại tiếp ∆BIC
 Xem đáp án
Xem đáp án
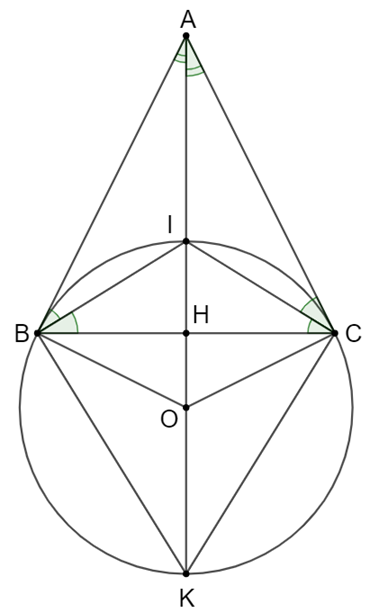
a) Vì tam giác ABC cân ở A => AI vừa là đường phân giác vừa là đường cao.
Do 3 điểm A, I, O thẳng hàng => AO BC
=> (1)
Vì OI = OC = R => ∆IOC cân tại O
=> (2)
Do CI là đường phân giác của nên suy ra (3)
Từ (1), (2) và (3) suy ra
Vậy AC là tiếp tuyến của đường tròn tâm O.
Câu 54:
b) Gọi H là trung điểm của BC. Kẻ đường kính IK của đường tròn (O).
Chứng minh: Xem đáp án
Xem đáp án
b) Do ∆CIK nội tiếp đường tròn (O)
(góc nội tiếp chắn nửa đường tròn)
=> CK CI
Mà CI là đường phân giác góc trong
=> CK là đường phân giác góc ngoài của
Nên theo tích chất đường phân giác ta có:
(đpcm).
Câu 55:
Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường tròn (O) lấy một điểm E bất kì (E khác A, B). Tiếp tuyến tại E của đường tròn (O) cắt Ax, By lần lượt tại C, D.
a) CM: CD = AC + BD.
 Xem đáp án
Xem đáp án
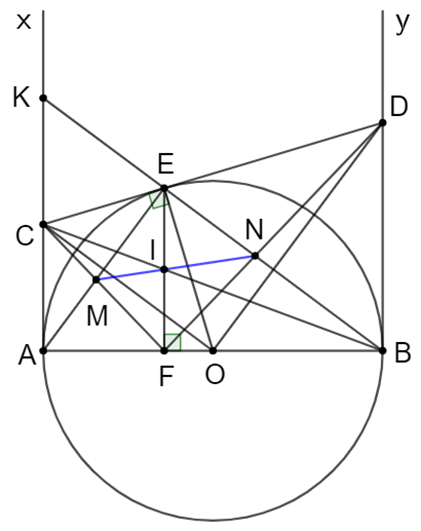
a) Theo tính chất 2 tiếp tuyến cắt nhau, ta có:
• Ax và CD là 2 tiếp tuyến cắt nhau tại C => CA = CE;
• By và CD là 2 tiếp tuyến cắt nhau tại D => DB = DE.
Suy ra: AC + BD = CE + DE = CD (đpcm)
Câu 56:
b) Vẽ EF vuông góc AB tại F, BE cắt AC tại K. CM: AF.BC = KE.EB.
 Xem đáp án
Xem đáp án
b) ΔAEB nội tiếp đường tròn đường kính AB
=> ΔAEB vuông tại E mà EF là đường cao
Áp dụng hệ thức lượng trong tam giác vuông, ta được: AF.AB = AE2 (1)
ΔBAK vuông tại A có AE là đường cao
Áp dụng hệ thức lượng trong tam giác vuông, ta được: KE.EB = AE2 (2)
Từ (1) và (2) suy ra: AF.AB = KE.EB (đpcm)
Câu 57:
c) EF cắt CB tại I. CM tam giác AFC đồng dạng với tam giác BFD, suy ra FE là tia phân giác của góc CFD.
 Xem đáp án
Xem đáp án
c) Ax // By (cùng AB), theo định lí Ta-lét ta có:
Mà CE = CA và ED = BD
=>
Lại có
Do đó ΔAFC ᔕ ΔBFD (c.g.c) (đpcm)
Câu 58:
d) EA cắt CF tại M. EB cắt DF tại N. CM: M, I, N thẳng hàng.
 Xem đáp án
Xem đáp án
d) Ta có: CA = CE; OA = OE => OC là đường trung trực của AE
Mà AE EB => OC // EB hay OC // BK
Lại có O là trung điểm của BC
=> C là trung điểm của AK => AC = CK
EF // AK =>
Mà AC = CK => IE = IF
Gọi P = IM Ax; Q = IN By
Ta có: CP // IF =>
PA // IE =>
Mà IE = IF => CP = MP => P là trung điểm của AC.
Chứng minh tương tự ta có Q là trung điểm của BD.
IE // BD =>
và
=> ΔPCI ᔕ ΔQBI (c.g.c)
=> P, I, Q thẳng hàng Þ M, I, N thẳng hàng (đpcm)
Câu 59:
Cho đường tròn (O), đường kính AB, vẽ các tiếp tuyến Ax, By. Từ M trên đường tròn (M khác A,B) vẽ tiếp tuyến thứ ba nó cắt Ax ở C cắt By ở D. Gọi N là giao điểm của BC và AD.
a) CMR:
 Xem đáp án
Xem đáp án
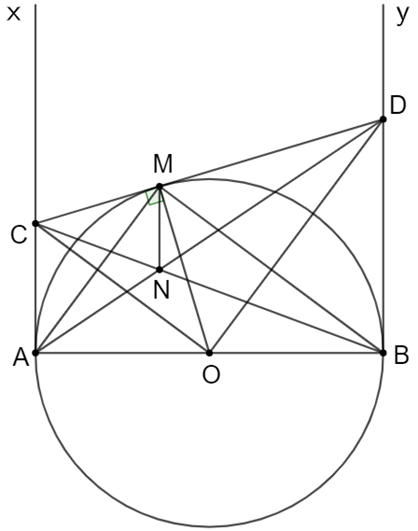
a) Ax là tiếp tuyến của đường tròn (O)
=> Ax AB => AC AB (1)
By là tiếp ruyến của đường tròn (O)
=> By AB => BD AB (2)
Từ (1) và (2) => AC // BD
Áp dụng định lý Ta-lét với AC // BD ta có:
(đpcm)
Câu 60:
 Xem đáp án
Xem đáp án
b) Theo tính chất 2 tiếp tuyến cắt nhau, ta có:
• Ax và CD là 2 tiếp tuyến cắt nhau tại C => CA = CM;
• By và CD là 2 tiếp tuyến cắt nhau tại D => DB = DM.
Ta có:
Vậy MN // BD (Theo định lí Ta-lét).
Mà BD AB => MN AB.
Câu 61:
c) Chứng minh rằng:
 Xem đáp án
Xem đáp án
c) Ta có: CA = CM (cmt) và OA = OM = R
=> OC là đường trung trực của đoạn thẳng MA
=> OC cũng là đường phân giác của ∆OMA
(3)
Lại có: DB = DM (cmt) và OB = OM = R
=> OD là đường trung trực của đoạn thẳng MB
=> OD cũng là đường phân giác của ∆OMB
(4)
Từ (3) và (4) ta suy ra
(đpcm).
Câu 62:
Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB tới đường tròn (O) với A, B là các tiếp điểm.
a) Chứng minh bốn điểm A, B, M, O cùng thuộc một đường tròn.
 Xem đáp án
Xem đáp án
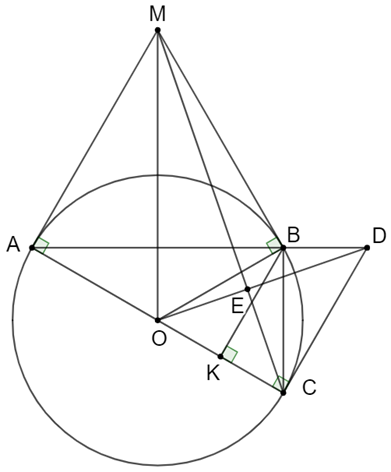
a) Xét tứ giác AOBM có:
=> AOBM là tứ giác nội tiếp đường tròn.
Vậy bốn điểm A, B, M, O cùng thuộc một đường tròn.
Câu 63:
b) Kẻ đường kính AC của đường tròn (O). Chứng minh OM // CB.
 Xem đáp án
Xem đáp án
b) Theo tính chất 2 tiếp tuyến cắt nhau, ta có:
MA và MB là 2 tiếp tuyến cắt nhau tại M => MA = MB.
Lại có OA = OB = R
=> OM là đường trung trực của đoạn thẳng AB
=> OM AB (1)
Mà (Do góc nội tiếp chắn nửa đường tròn)
=> AB BC (2)
Từ (1) và (2) => OM // BC
Câu 64:
c) Vẽ BK vuông góc với AC tại K. Chứng minh: CK.OM = OB.CB.
 Xem đáp án
Xem đáp án
c) Do OM // BC (Hai góc ở vị trí đồng vị)
=>
Lại có OM là đường trung trực trong tam giác cân OAB nên nó cũng là đường phân giác của tam giác OAB
Nên suy ra
Xét ∆BCK và ∆MOB có:
(cmt)
Þ ∆BCK ᔕ ∆MOB (g.g)
(đpcm)
Câu 65:
d) Tiếp tuyến tại C của đường tròn (O) cắt AB tại D. Chứng minh OD CM.
 Xem đáp án
Xem đáp án
d) Lấy E là giao điểm của CM và OD.
Ta có: (Hai góc cùng phụ với )
Mà (Hai góc nội tiếp cùng chắn cung BO)
Xét ∆BMO và ∆BCD có:
(cmt)
=> ∆BMO ᔕ ∆BCD (g.g)
Mà
=> ∆MBC ᔕ ∆OBD (c.g.c)
=> Tứ giác BMOE nội tiếp đường tròn
(Hai góc nôij tiếp cùng chắn cung MO)
=> OD CM (đpcm).
Câu 66:
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Đường thẳng d thay đổi đi qua M cắt đường tròn tại 2 điểm phân biệt C và D (C nằm giữa M và D)
a) Chứng minh tứ giác AMBO nội tiếp
 Xem đáp án
Xem đáp án
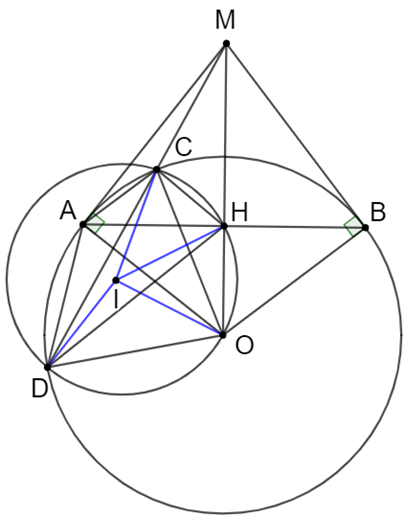
a) Xét tứ giác AOBM với và có:
Do đó AOBM là tứ giác nội tiếp đường tròn.
Câu 67:
b) Chứng minh MA2 = MC.MD
 Xem đáp án
Xem đáp án
b) Xét ∆MCA và ∆MAD có:
(góc tạo bởi tia tiếp tuyến và dây cung, góc nội tiếp đường tròn cùng chắn cung AC)
là góc chung
=> ∆MCA ᔕ ∆MAD (g.g)
Câu 68:
c) Chứng minh đường tròn ngoại tiếp tam giác OCD luôn đi qua điểm cố định khác O
 Xem đáp án
Xem đáp án
c) Lấy H là giao điểm của MO và AB.
Vì I là tâm đường tròn ngoại tiếp tam giác COD
Áp dụng hệ thức lượng trong tam giác vuông MAO vuông tại A có AH là đường cao nên suy ra MA2 = MH.MO.
Mà MA2 = MC.MD (cmt)
=> MH.MO = MC.MD
=>
Xét ∆MHD và ∆MCO có:
(cmt)
góc chung
=> ∆MHD ᔕ ∆MCO (g.g)
=> Tứ giác CHOD nội tiếp đường tròn (Hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại với hai góc bằng nhau).
=> H thuộc đường tròn (I).
Vậy (I) đi qua điểm cố định H là giao của MO và AB; với A, B là hai tiếp điểm từ điểm M cố định đến đường tròn (O).
Câu 69:
2(x − 1) = 7 + (−3)
 Xem đáp án
Xem đáp án
2(x − 1) = 7 + (−3)
<=> 2(x − 1) = 4
<=> x − 1 = 4 : 2
<=> x − 1 = 2
<=> x = 3.
Vậy nghiệm của phương trình là x = 3.
Câu 70:
Tìm x, biết:
a)
 Xem đáp án
Xem đáp án
a)
+ TH1: x − 1,7 = 2,3
<=> x = 2,3 + 1,7
<=> x = 4
+TH2: x − 1,7 = −2,3
<=> x = −2,3 + 1,7
<=> x = −0,6.
Vậy nghiệm của phương trình là x = 4 và x = −0,6.
Câu 72:
a) Chứng minh tứ giác ABEF nội tiếp.
 Xem đáp án
Xem đáp án
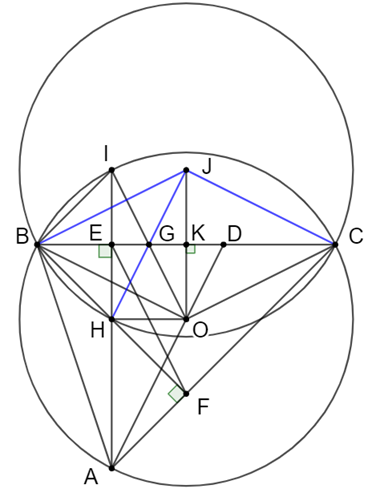
a) Tứ giác ABEF có 2 đỉnh kề nhau cùng nhìn cung BA với hai góc bằng nhau:
Do đó tứ giác ABEF nội tiếp đường tròn.
Câu 73:
 Xem đáp án
Xem đáp án
b) Tứ giác EBAF nội tiếp đường tròn.
(Hai góc nội tiếp cùng chắn cung BE).
Lại có:
Và
Xét ∆ABC và ∆EFC có:
(cmt)
: góc chung
=> ∆ABC ᔕ ∆EFC (g.g)
Câu 74:
 Xem đáp án
Xem đáp án
c) Ta có: (Hai góc nội tiếp cùng chắn cung IC)
Lại có: (Hai góc nội tiếp cùng chắn cung EF)
=>
=> BE là đường phân giác của góc
Mà BE cũng là đường cao của ∆IBH nên ∆IBH là tam giác cân tại B có BE là đường trung trực của cạnh HI.
Vậy H và I đối xứng với nhau qua BC.
Câu 75:
d) Gọi K là hình chiếu của O trên BC. Chứng minh tỉ số không đổi và H chạy trên một cung tròn cố định khi A chuyển động trên cung lớn BC.
 Xem đáp án
Xem đáp án
d) D, E lần lượt là giao của AO và AI với BC.
Do OK // EI nên theo định lí Ta-lét ta có:
Và (Hai góc ở vị trí so le trong) (1)
Do OK // EA nên theo định lí Ta-lét ta có:
Và (Hai góc ở vị trí đồng vị) (2)
Ta có:
(*)
Tam giác OIA cân tại O do có OI = OA (3)
Từ (1), (2), (3) suy ra
=> OK là đường phân giác của tam giác DOG mà OK cũng là đường cao nên OK là đường trung trực của tam giác DOG cân tại O
=> GK = DK
Khi đó (*) trở thành:
Vậy tỉ số không đổi.
Do BC cố định nên ta luôn xây dựng được một đường tròn (J) là đường tròn ngoại tiếp của tam giác HBC. Vậy nên H luôn chuyển động trên một cung cố định.
Câu 76:
Cho đường tròn tâm O và BC là dây cung không đi qua tâm. Trên tia đối của tia BC lấy điểm M sao cho M không trùng với B. Đường thẳng đi qua M cắt đường tròn (O) đã cho tại N và P (N nằm giữa M và P) sao cho O nằm trong PMC. Gọi A là điểm chính giữa của cung nhỏ NP. Các dây AB và AC lần lượt cắt NP tại D và E.
a) Chứng minh tứ giác BDEC nội tiếp.
 Xem đáp án
Xem đáp án
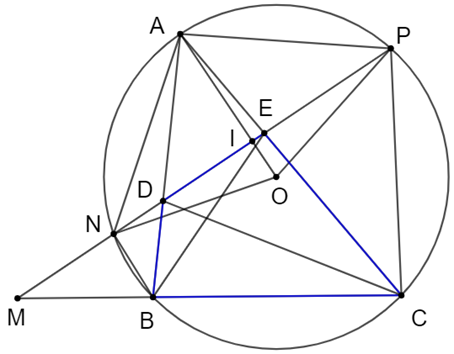
a) Gọi I là giao điểm của OA và NP
Ta có độ dài cung AN bằng độ dài cung AP nên suy ra AN = AP
Và ON = OP = R.
=> OA là đường trung trực của đoạn thẳng NP
=> OA NP tại I
=>
Hay
Lại có: OA = OB => ∆OAB cân tại O.
Suy ra
Mà (Hai góc đối đỉnh)
Đường tròn (O) có: là góc nội tiếp chắn cung AB và là góc ở tâm chắn cung AB nên suy ra:
Hay
Tứ giác BNDC có
Suy ra BNDC là tứ giác nội tiếp.
Câu 77:
 Xem đáp án
Xem đáp án
b) BNPC là tứ giác nội tiếp nên suy ra
Lại có
Xét ∆MBN và ∆MPC có:
(cmt)
: góc chung
=> ∆MBN ᔕ ∆MPC (g.g).
Câu 78:
 Xem đáp án
Xem đáp án
Ta có:
6x2 − 3xy + x = 1 − y
<=> 6x2 − 3xy + x + y − 1 = 0
<=> (6x2 − 2x) − (3xy − y) + (3x − 1) = 0
<=> (6x2 − 2x) − (3xy − y) + (3x − 1) = 0
<=> 2x(3x − 1) − y(3x − 1) + (3x − 1) = 0
<=> (2x − y + 1)(3x − 1) = 0
+ TH1: 2x − y + 1 = 0
<=> y = 2x + 1 (1)
Thay (1) vào phương trình x2 + y2 = 1 ta được
x2 + (2x + 1)2 = 1
<=> x2 + 4x2 + 4x + 1 = 1
<=> 5x2 + 4x = 0
<=> x(5x + 4) = 0
• Với x = 0, thay vào (1) ta được y = 1.
• Với , thay vào (1) ta được
+ TH2: 3x − 1 = 0
(2)
Thay (2) vào phương trình x2 + y2 = 1 ta được
Vậy nghiệm của hệ phương trình trên là
Câu 79:
Vẽ đồ thị hàm số
a) Tìm trên đồ thị điểm A có tung độ bằng −2;
 Xem đáp án
Xem đáp án
Đồ thị hàm số đi qua gốc tọa độ O(0;0) và điểm
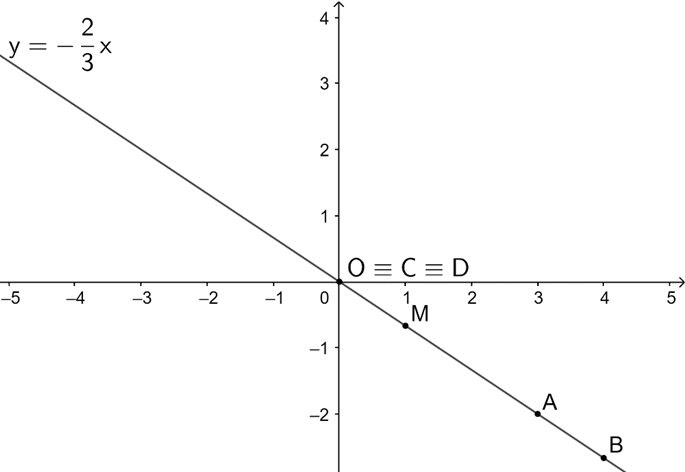
a) A là điểm trên đồ thị có tung độ bằng −2.
Khi đó
Vậy A(3; −2).
Câu 80:
 Xem đáp án
Xem đáp án
b) B là điểm trên đồ thị có hoành độ bằng 4.
Khi đó
VậyCâu 81:
 Xem đáp án
Xem đáp án
c) C là điểm trên đồ thị sao cho tung độ bằng 3 lần hoành độ hay
Khi đó
Vậy
Câu 82:
 Xem đáp án
Xem đáp án
d) D là điểm trên đồ thị có tung độ và hoành độ đối nhau hay
Khi đó
Vậy
Câu 83:
Cho đường thẳng (d): y = x − 2. Điểm A nằm trên (d) có hoành độ và tung độ đối nhau sẽ có tọa độ là (a; b).
Khi đó, a.b = … Xem đáp án
Xem đáp án
Vì A có hoành độ và tung độ đối nhau nên a = − b (1)
Vì A nằm trên d nên b = a − 2 (2)
Thay (2) vào (1) ta được: a = − (a − 2)
<=> a = − a + 2
<=> a = 1
Suy ra b = − a = −1.
Vậy khi đó a.b = −1.
Câu 86:
Tổng của hai số là 19,1. Nếu giảm số hạng thứ nhất đi 4 lần và giữ nguyên số hạng thứ hai thì được tổng mới là 7,4. Tìm hai số đó.
 Xem đáp án
Xem đáp án
Tổng mới giảm số đơn vị là:
19,1 − 7,4 = 11,7.
Do ở tổng mới số hạng thứ nhất bị giảm đi 4 lần nên số hạng thứ nhất còn lại 3 phần trên tổng 4 phần. Khi đó, số hạng thứ nhất là:
11,7 : 3 × 4 = 15,6.
Số hạng thứ hai là:
19,1 − 15,6 = 3,5.
Đáp số: Số hạng thứ nhất: 15,6; số hạng thứ hai là: 3,5.
Câu 87:
Có ba chiếc hộp A, B, C mỗi chiếc hộp chứa ba chiếc thẻ được đánh số 1, 2, 3. Từ mỗi hộp rút ngẫu nhiên một chiếc thẻ. Gọi P là xác suất để tổng số ghi trên ba tấm thẻ là 6. Khi đó P bằng:
 Xem đáp án
Xem đáp án
Chọn C
Ta có: n(Ω) = 3.3.3 = 27.
Gọi A là: “Tổng số ghi trên ba tấm thẻ là 6”.
Để tổng số ghi trên ba tấm thẻ là 6 thì có các tổng sau:
1 + 2 + 3 = 6. Khi đó hoán vị 3 phần tử 1, 2, 3 ta được 3! = 6 (cách).
2 + 2 + 2 =6. Khi đó ta có 1 cách.
Do đó n(A) = 6 + 1 = 7.
Vậy
Câu 88:
Chọn ngẫu nhiên ba số đôi một khác nhau từ tập hợp {1; 2; 3; ...; 100} gồm 100 số nguyên dương đầu tiên. Tính xác suất để 3 số được chọn là độ dài 3 cạnh của một tam giác.
 Xem đáp án
Xem đáp án
Số phần tử của không gian mẫu là
Ta tính số cách chọn ba phần tử khác nhau của tập hợp A sao cho ba phần tủ nhày là độ dài ba cạnh một tam giác.
Giả sử ba số cần chọn là x < y < z. Khi đó ta phải có x > z − y.
Đặt k = z − y; 1 k 49.
Với k = 1, ta có x {2; 3; …; 98}. Ta xét từng trường hợp như sau:
+ x = 2 các bộ số (y; z) lượt là (3; 4), (4; 5), …, (99; 100) có 97 bộ.
+ x = 3 các bộ số (y; z) lượt là (4; 5), (5; 6), …, (99; 100) có 96 bộ.
…
+ x = 8 chỉ có 1 bộ số (y; z) = (99; 100) thỏa mãn.
Do đó số bộ ba trong trường hợp này là
Với k = 2, ta có x {3; 4; …; 97}. Ta xét từng trường hợp như sau:
+ x = 3 các bộ số (y; z) lượt là (4; 6), (5; 7), …, (98; 100) có 95 bộ.
…
+ x = 97 chỉ có 1 bộ số (y; z) = (98; 100) thỏa mãn.
Như vậy trường hợp này số bộ ba là
Lập luận tương tự đến trường hợp k = 49 thì x = 50 và chỉ có một bộ số (y; z) thỏa mãn là (51; 100).
Vậy số cách chọn bộ ba số thỏa mãn yêu cầu là
Xác suất của biến cố cần tìm là
Câu 89:
 Xem đáp án
Xem đáp án
+ TH1: Nếu x chẵn, ta đặt: x = 2k, với k ℕ.
=> x2 + 1 = 4k2 + 1 không chia hết cho 4 .
+ TH2: Nếu x chẵn, ta đặt: x = 2k + 1, với k ℕ.
=> x2 + 1 = 4k2 + 4k + 2 = 4k(k + 1) + 2.
Vì 4k(k + 1) ⋮ 4 => 4k(k + 1) + 2 chia cho 4 dư 2
=> 4k(k + 1) + 2 không chia hết cho 4.
Vậy với x ℕ thì x2 + 1 không chia hết cho 4.
Câu 90:
 Xem đáp án
Xem đáp án
Chọn B
+ Xét đáp án A. Khi n = 3 thì giá trị của n2 + 11n + 2 bằng 44, chia hết cho 11
Nên đáp án A đúng.
+ Xét đáp án B. Khi n = 2k, k ℕ.
=> n2 + 1 = 4k2 + 1 không chia hết cho 4, k ℕ.
Khi n = 2k + 1, với k ℕ.
=> x2 + 1 = 4k2 + 4k + 2 = 4k(k + 1) + 2, k ℕ.
Nên đáp án B sai.
+ Xét đáp án C. Tồn tại số nguyên tố 5 chia hết cho 5 nên đáp án C đúng.
+ Xét đáp án D. Phương trình 2x2 − 8 = 0
<=> x2 = 4
<=> x = ± 2 ℤ.
Nên đáp án D đúng.
Câu 91:
Cho tam giác ABC vuông tại A có đường cao AH.
Chứng minh rằng:
 Xem đáp án
Xem đáp án
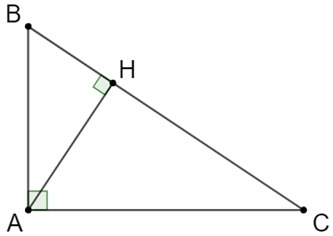
Do ∆ABC là tam giác vuông tại A nên:
Mặt khác theo định lý Pytago thì:
BC2 = AB2 + AC2
Do đó ta có đpcm.
Câu 92:
Cho 4 điểm O, A, B, C sao cho
Chứng minh: A, B, C thẳng hàng.
 Xem đáp án
Xem đáp án
Vậy 3 điểm A, B, C thẳng hàng.
Câu 93:
Một liên đội thiếu niên khi xếp hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người. Tính số đội viên của liên đội biết rằng số đội viên khoảng từ 100 đến 150?
 Xem đáp án
Xem đáp án
Gọi số đội viên là a.
Ta có: a chia 2, 3, 4, 5 đểu dư 1 => a − 1 chia hết cho 2, 3, 4, 5
=> a − 1 BC(2, 3, 4, 5).
Mà BCNN(2, 3, 4, 5) = 60
=> a − 1 B(60) = {0; 60; 120; 180; 240; …}
Vì a − 1 thuộc khoảng 100 đến 150
=> a − 1 = 120
=> a = 121
Vậy liên đội đó có 121 đội viên.
Câu 94:
Cho hàm số . Tìm m để (C) cắt d: y = x + m tại hai điểm phân biệt a, b sao cho tam giác OAB vuông tại A hoặc B.
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm:
Để hai đồ thị hàm số cắt nhau ở hai điểm thì phương trình (1) phải có hai nghiệm phân biệt
<=> ∆ = (m − 3)2 − 4(1 − m) > 0
<=> (m − 1)2 + 4 > 0 (luôn đúng với mọi m)
Khi đó x1, x2 là hai nghiệm của phương tình trên thì A(x1; x1 + m) và B(x2; x2 + m) là hai giao điểm của 2 đồ thị hàm số.
Không mất tính tổng quát, giả sử tam giác OAB vuông tại A.
=> x1(x2 − x1) + (x2 − x1)(x1 + m) = 0
Áp dụng định lí Vi-ét:
(thỏa mãn)
Vậy
Câu 95:
Cho hàm số có đồ thị (C) và đường thẳng d: y = x + m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C(−2; 5), giá trị của tham số m để tam giác ABC đều là bao nhiêu?
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của (C) và đường thẳng d:
(1)
Khi đó cắt (C) tại hai điểm phân biệt A và B khi và chi khi phương trình (1) có hai nghiệm phân biệt khác 1
(luôn đúng)
Gọi A(x1; x1 + m); B(x2; x2 + m) trong đó x1; x2 là nghiệm của (1), theo Viet ta có:
Gọi là trung điểm của AB, suy ra , nên
Mặt khác
Vậy tam giác ABC đều khi và chỉ khi
<=> 2m2 + 8m − 10 = 0
Câu 96:
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, AB = 2a, AC = a và SA vuông góc với mặt phẳng (ABC). Biết góc giữa hai mặt phẳng (SAB) và (SBC) bằng 60°. Tính thể tích của khối chóp S.ABC.
 Xem đáp án
Xem đáp án
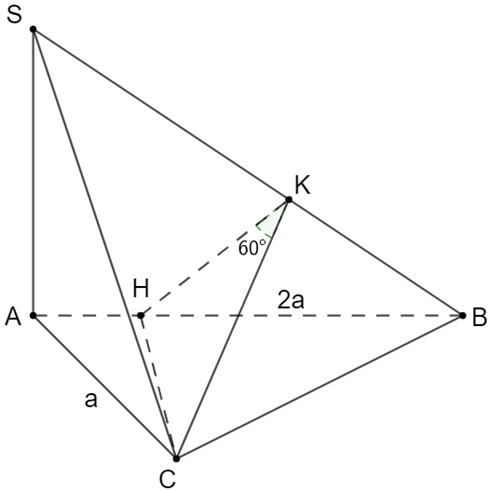
Trong ∆ABC kẻ CH AB
Mà SA CH (SA (SAB))
=> CH (SAB) => CH SB (1)
Trong ∆SAB kẻ HK SB (2)
Từ (1) và (2) => SB (HKC)
=> SB KC
Góc giữa hai mặt phẳng (SAB) và (SBC) là
Trong tam giác vuông CKH có:
Xét ∆SAB và ∆HKB có:
: góc chung
=> ∆SAB ᔕ ∆HKB (g.g)
Thể tích của khối chóp S.ABC là:
Tam giác HKA vuông tại H (vì AH (SBC), HK (SBC))
Câu 97:
Cho hình chóp S.ABC có đường cao SA = 2a, tam giác ABC vuông ở C có AB = 2a, . Gọi H là hình chiếu vuông của A trên SC. Tính theo a thể tích của khối chóp H.ABC. Tính cosin của góc giữa hai mặt phẳng (SAB), (SBC).
 Xem đáp án
Xem đáp án
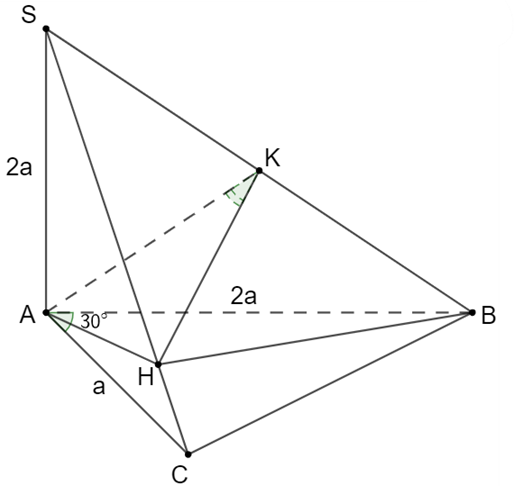
Trong mặt phẳng (SAC), kẻ HI // SA thì HI (ABC).
Ta có:
Do đó:
Ta có:
Vậy
Gọi K là hình chiếu vuông góc của A lên SB. Ta có:
AH SC, AH CB (Do CB (SAC)).
=> AH (SBC) => AH SB
Lại có: SB AK => SB (AHK).
Do đó, góc giữa hai mặt phẳng (SAB), (SBC) là
Câu 98:
Phân tích đa thức thành nhân tử:
a) 7x2y − 14xy2 + 21x
 Xem đáp án
Xem đáp án
a) 7x2y − 14xy2 + 21x2y2
= 7xy(x − 2y + 3xy).
Câu 99:
b) 2x(x − y) + 3y(y − x)
 Xem đáp án
Xem đáp án
b) 2x(x − y) + 3y(y − x)
= 2x(x − y) − 3y(x − y)
= (x − y)(2x − 3y).
Câu 100:
c) 6x(x − 3) + 2x − 6
 Xem đáp án
Xem đáp án
c) 6x(x − 3) + 2x − 6
= 6x(x − 3) + 2(x − 3)
= (x − 3)(6x + 2)
= 2(x − 3)(3x + 1).
Câu 101:
d) 4x(x − y)2 + 3x − 3y
 Xem đáp án
Xem đáp án
d) 4x(x − y)2 + 3x − 3y
= 4x(x − y)2 + 3(x − y)
= (x − y)[4(x − y) + 3]
= (x − y)(4x − 4y + 3).
Câu 102:
Tính: (14xy2 + 21x2y − 7x3) : 7x
 Xem đáp án
Xem đáp án
(14xy2 + 21x2y − 7x3) : 7x
= 7x.(2y2 + 21x2y − 7x2) : 7x
= 2y2 + 21x2y − 7x2.
Câu 103:
Đọc tên góc, đỉnh, và các cạnh của góc trong các hình vẽ sau:
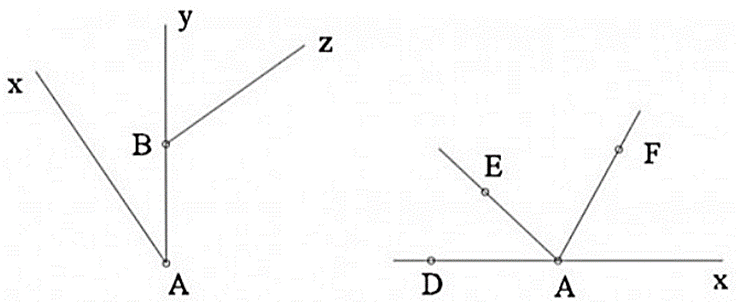
 Xem đáp án
Xem đáp án
Góc đỉnh A, cạnh Ax và Ay;
Góc đỉnh B, cạnh By và Bz;
Góc đỉnh B, cạnh Bz và BA;
Góc đỉnh A, cạnh AD và AE;
Góc đỉnh A, cạnh AE và AF;
Góc đỉnh A, cạnh AF và Ax;
Góc đỉnh A, cạnh AD và AF;
Góc đỉnh A, cạnh AE và Ax.
Câu 104:
Đọc tên góc, đỉnh và các cạnh của góc trong Hình 85 và Hình 86.
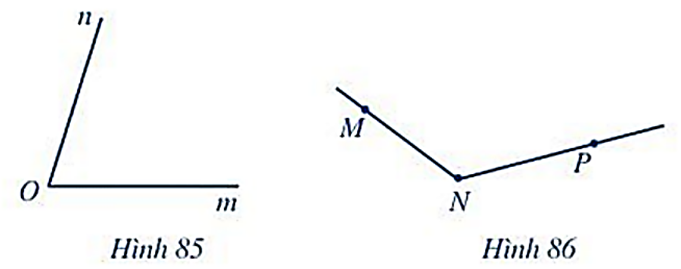
 Xem đáp án
Xem đáp án
Hình 85. Góc có đỉnh là O, cạnh của góc là Om và On.
Hình 86. Góc có đỉnh là N, cạnh của góc là NM và NP.
Câu 105:
 Xem đáp án
Xem đáp án
x3 + y3 + z3 − 3xyz = (x + y)3 − 3xy(x + y) + z3 − 3xyz
= [(x + y)3 + z3] − [3xy(x + y) + 3xyz]
= (x + y + z)[(x + y)2 − (x + y)z + z2] − 3xy(x + y + z)
= (x + y + z)(x2 + 2xy + y2 − xz − yz + z2 − 3xy)
= (x + y + z)(x2 + y2 + z2 − xy − xz − yz).
Câu 106:
 Xem đáp án
Xem đáp án
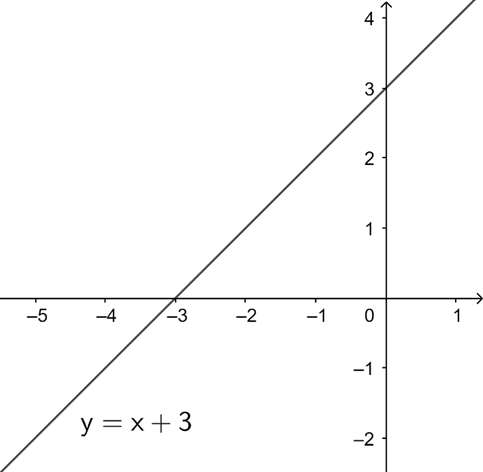
a) Với m = 2 => y = x + 3 (d)
• Nếu x = 0 thì y = 3;
• Nếu y = 0 thì x = −3.
Vậy (d) đi qua hai điểm (0; 3) và (−3; 0).
Câu 107:
 Xem đáp án
Xem đáp án
b) Để đường thẳng (d) song song với đường thẳng y = 2x + 1 thì m − 1 = 2 <=> m = 3.
Vậy m = 3 là giá trị của m thỏa mãn.
Câu 108:
c) Tính khoảng cách là gốc tọa độ đến đường thẳng được vẽ ở ý (a)
 Xem đáp án
Xem đáp án
c) Khoảng cách từ O đến đường thẳng (d’): x − y + 3 = 0 là
Câu 109:
a) Vẽ đồ thị hàm số khi m = −2.
 Xem đáp án
Xem đáp án
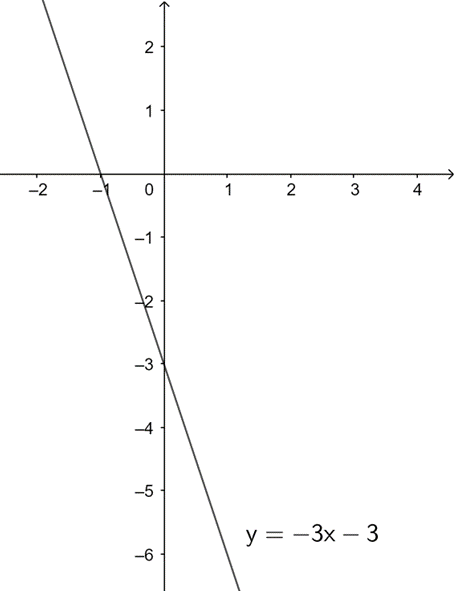
a) Với m = −2 Þ y = − 3x − 3 (d)
• Nếu x = 0 thì y = −3;
• Nếu y = 0 thì x = 1.
Vậy (d) đi qua hai điểm (0; 3) và (1; 0).
Câu 110:
 Xem đáp án
Xem đáp án
b) Để đồ thị hàm số cắt đường thẳng y = 2x + 5 tại điểm có hoành độ bằng 4 thì
(m − 1).4 − 3 = 2.4 + 5
<=> 4m − 4 − 3 = 13
<=> 4m = 20 Û m = 5
Vậy m = 5 là giá trị của m cần tìm.
Câu 111:
c) Tìm m để đường thẳng (d) tạo với 2 trục tọa độ một tam giác có diện tích bằng 3
 Xem đáp án
Xem đáp án
c) Đường thẳng (d): y = (m − 1)x − 3 giao với trục Ox tại điểm có tọa độ (m ≠ 1)
Đường thẳng (d): y = (m − 1)x − 3 giao với trục Oy tại điểm có tọa độ B(0; −3)
=> OB = 3
Suy ra tam giác đó có diện tích là
Vậy để diện tích của tam giác bằng 3 thì:
(TMĐK)
Vậy và là các giá trị của m thỏa mãn yêu cầu bài toán.
Câu 112:
Số hạng nào chứa x với số mũ tự nhiên trong khai triển sau:
a)
 Xem đáp án
Xem đáp án
a)
Để số hạng chứa x có số mũ tự nhiên thì
Và
Vậy số hạng chứa x với số mũ tự nhiên trong khai triển sau:
Câu 113:
 Xem đáp án
Xem đáp án
b)
Để số hạng chứa x có số mũ tự nhiên thì
Và
Vậy số hạng chứa x với số mũ tự nhiên trong khai triển sau:
Câu 114:
Giá trị nào của m để điểm I(−1; 6) là điểm cực đại của đồ thị hàm số y = x3 − 3mx2 − 9x + 1 (Cm).
 Xem đáp án
Xem đáp án
Ta có
Để I(−1; 6) là điểm cực đại của đồ thị hàm số y = x3 − 3mx2 − 9x + 1 (Cm) thì trước hết x = −1 là nghiệm của phương trình 3x2 − 6mx − 9 = 0.
<=> 3(−1)2 − 6m(−1) − 9 = 0
<=> 3 + 6m − 9 = 0
<=> m = 1.
Thử lại với m = 1 ta được:
(Cm)
Khi đó với x = −1 ta có y = 6. Vây I(−1; 6) là điểm thuộc đồ thị hàm số.
Lại có
Ta xét BBT:
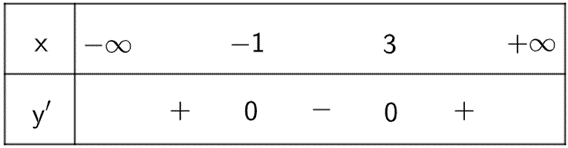
Dựa vào BBT ta thấy x = −1 là điểm cực địa của đồ thị hàm số
Vậy để điểm I(−1; 6) là điểm cực đại của đồ thị hàm số y = x3 − 3mx2 − 9x + 1 (Cm) thì m = 1.
Câu 115:
Biết M(1; −6) là điểm cực đại của đồ thị hàm số y = 2x3 + bx2 + cx + 1. Tìm tọa độ điểm cực tiểu của đồ thị hàm số đó.
 Xem đáp án
Xem đáp án
Vì M(1; −6) là điểm cực đại của đồ thị hàm số nên x = 1 là nghiệm của y' = 0, đồng thời M thuộc đồ thị
Thay vào y' ta có:
=> 6x2 + 6x − 12 = 0
<=> 6x2 − 6x + 12x − 12 = 0
<=> 6x(x − 1) + 12(x − 1) = 0
<=> 6(x − 1)(x + 2) = 0
Suy ra nghiệm còn lại là x = −2 là điểm CT của hàm số
=> y = 21
Suy ra tọa độ điểm CT của đồ thị hàm số là N(−2; 21).
Câu 116:
Giải hệ phương trình:
 Xem đáp án
Xem đáp án
(*)
Ta đặt: a = x + y và b = xy (Với a2 ≥ − 4b)
Hệ phương trình (*) trở thành
+ TH1:
+ TH2:
Vậy cặp nghiệm (x; y) của hệ phương trình là:
Câu 117:
Giải hệ phương trình:
 Xem đáp án
Xem đáp án
(*)
Ta đặt: a = x + y và b = xy (Với a2 ≥ − 4b)
Hệ phương trình (*) trở thành
+ TH1:
+ TH2:
Vậy cặp nghiệm (x; y) của hệ phương trình là:
Câu 118:
Tìm 3 số hạng liên tiếp của một cấp số cộng, biết tổng của chúng là 27 và tổng các bình phương của chúng là 293.
 Xem đáp án
Xem đáp án
Gọi 3 số hạng lần lượt là x, x + d, x + 2d (với d là công sai của cấp số cộng).
Do tổng của chúng là 27 nên ta có: x + x + d + x + 2d = 27
<=> 3x + 3d = 27
<=> x + d = 9
<=> d = 9 – x.
Tổng các bình phương của chúng là 293 nên suy ra:
x2 + (x + d)2 + (x + 2d)2 = 293
<=> x2 + (x + 9 − x)2 + (x + 18 − 2x)2 = 293
<=> x2 + 92 + (18 − x)2 = 293
<=> x2 + 81 + 324 − 36x + x2 = 293
<=> 2x2 − 36x + 112 = 0
<=> x2 − 18x + 56 = 0
<=> (x − 14)(x − 4) = 0
• TH1: Với x = 14, d = −5 thì 3 số hạng cần tìm là 14; 9; 4;
• TH2: Với x = 4, d = 5 thì 3 số hạng cần tìm là 4; 9; 14.
Vậy 3 số hạng liên tiếp cần tìm là 4; 9; 14 hoặc 14; 9; 4.
Câu 119:
Tìm cấp số cộng có 3 số hạng liên tiếp, biết tổng số của chúng là 15 và tổng bình phương các số hạng là 83.
 Xem đáp án
Xem đáp án
Gọi 3 số hạng2 lần lượt là x; x + d; x + 2d (với d là công sai của cấp số cộng).
Do tổng của chúng là 15 nên ta có:
x + x + d + x + 2d = 15
<=> 3x + 3d = 15
<=> x + d = 5
<=> d = 5 – x.
Tổng các bình phương của chúng là 83 nên suy ra
x2 + (x + d)2 + (x + 2d)2 = 83
<=> x2 + (x + 5 − x)2 + (x + 10 − 2x)2 = 83
<=> x2 + 52 + (10 − x)2 = 83
<=> x2 + 25 + 100 − 20x + x2 = 83
<=> 2x2 − 20x + 42 = 0
<=> x2 − 10x + 21 = 0
<=> (x − 3)(x − 7) = 0
• TH1: Với x = 3, d = 2 thì 3 số hạng cần tìm là 3; 5; 7;
• TH2: Với x = 7, d = −2 thì 3 số hạng cần tìm là 7; 5; 3.
Vậy 3 số hạng liên tiếp cần tìm là 3; 5; 7 hoặc 7; 5; 3.
Câu 120:
Nêu tính chất đối xứng của hình vuông, hình chữ nhật, hình thoi, hình bình hành.
 Xem đáp án
Xem đáp án
• Hình bình hành:
Hình bình hành có bốn cạnh; những cạnh đối nhau thì song song và bằng nhau.
• Hình thoi:
Hình thoi có bốn cạnh bằng nhau; những cạnh đối diện song song với nhau.
• Hình chữ nhật:
Hình chữ nhật có bốn cạnh và bốn góc vuông. Những cạnh đối nhau thì song song và bằng nhau.
• Hình vuông:
Hình vuông có bốn cạnh bằng nhau và bốn góc vuông.
Câu 121:
Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.
 Xem đáp án
Xem đáp án
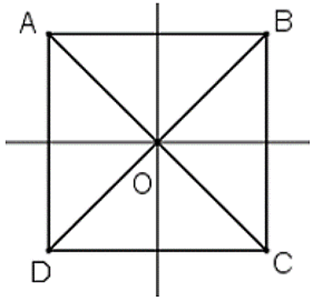
• Hình vuông cũng là hình bình hành nên nhận O là giao điểm của hai đường chéo là tâm đối xứng.
• Hình vuông cũng là hình thoi nên nhận hai đường chéo AC và BD là các trục đối xứng.
• Hình vuông cũng là hình thang cân nên nhận đường thẳng nối trung điểm các cặp cạnh đối diện là trục đối xứng.
Vậy hình vuông có 1 tâm đối xứng và 4 trục đối xứng như trên.
