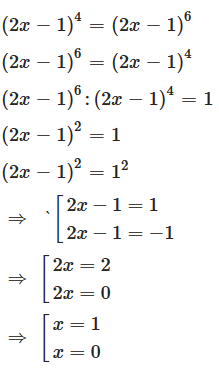- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 32)
-
11824 lượt thi
-
50 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Giải phương trình sinx + cosx = cos2x.
 Xem đáp án
Xem đáp án
Ta có
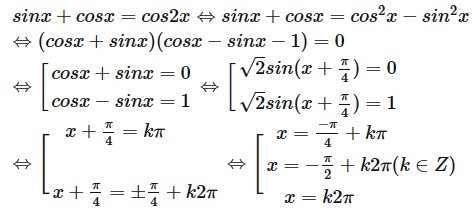
Vậy phương trình có nghiệm \(x = \frac{{ - \pi }}{4} + k\pi \), \(x = \frac{{ - \pi }}{2} + k2\pi \), x = k2π (k ∈ ℤ).
Câu 2:
Cách đây vài năm, ngày 20 tháng 3 là Chủ nhật. Hỏi ngày 20 tháng 11 năm đó là ngày thứ mấy?
 Xem đáp án
Xem đáp án
Từ 20/3 đến 20/11 trong 1 năm có số ngày là:
365 – 10 – 31 – 31 – 28 – 20 = 245 (ngày)
Ta có:
245 : 7 = 35
Vậy ngày 20/11 năm đó cũng là ngày Chủ nhật.
Câu 3:
Rút gọn
a) \(\sqrt {8 + 2\sqrt 7 } - \sqrt {8 - 2\sqrt 7 } \);
b) \(\sqrt {3 + 2\sqrt 2 } - \sqrt {6 - 4\sqrt 2 } \).
 Xem đáp án
Xem đáp án
a) Ta có
\[\sqrt {8 + 2\sqrt 7 } - \sqrt {8 - 2\sqrt 7 } = \sqrt {{{\left( {1 + \sqrt 7 } \right)}^2}} - \sqrt {{{\left( {1 - \sqrt 7 } \right)}^2}} \]
\[ = \left| {1 + \sqrt 7 } \right| - \left| {1 - \sqrt 7 } \right|\]\( = 1 + \sqrt 7 + 1 - \sqrt 7 = 2\)
b) Ta có
\(\sqrt {3 + 2\sqrt 2 } - \sqrt {6 - 4\sqrt 2 } = \sqrt {{{\left( {1 + \sqrt 2 } \right)}^2}} - \sqrt {{{\left( {2 - \sqrt 2 } \right)}^2}} \)
\( = \left| {1 + \sqrt 2 } \right| - \left| {2 - \sqrt 2 } \right| = 1 + \sqrt 2 - 2 + \sqrt 2 = 2\sqrt 2 - 1\)
Câu 4:
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
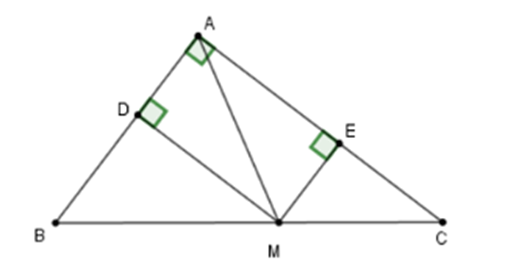
Xét tứ giác ADME có
\(\widehat {DA{\rm{E}}} = \widehat {A{\rm{E}}M} = \widehat {A{\rm{D}}M} = 90^\circ \)
Suy ra ADME là hình chữ nhật
Do đó AM = DE
Để DE nhỏ nhất thì AM nhỏ nhất
Khi đó M là hình chiếu của A trên BC
Vậy ta chọn đáp án A.
Câu 5:
Một ô tô đi từ Hà Nội lúc 8 giờ sáng, dự kiến đến Hải Phòng vào lúc 10 giờ 30 phút. Nhưng mỗi giờ ô tô đã đi chậm hơn so với dự kiến là 10km nên mãi đến 11 giờ 20 phút xe mới tới Hải Phòng. Tính quãng đường Hà Nội – Hải Phòng.
 Xem đáp án
Xem đáp án
Gọi x (km) là quãng đường Hà Nội – Hải Phòng. Điều kiện: x > 0
Thời gian dự định đi:
10 giờ 30 phút – 8 giờ = 2 giờ 30 phút = \(\frac{5}{2}\) giờ
Thời gian thực tế đi:
11 giờ 20 phút – 8 giờ = 3 giờ 20 phút = \(\frac{{10}}{3}\) giờ.
Vận tốc dự định đi là \(x:\frac{5}{2} = \frac{{2x}}{5}\) (km/h).
Vận tốc thực tế đi là \(x:\frac{{10}}{3} = \frac{{3x}}{{10}}\) (km/h).
Vận tốc thực tế đi chậm hơn vận tộc dự định đi 10 km/h nên ta có phương trình:
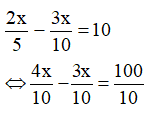
Suy ra x = 100 (thỏa mãn)
Vậy quãng đường Hà Nội – Hải Phòng dài 100 km.
Câu 6:
Phép quay tâm I(4; – 3) góc quay 180° biến đường thẳng d: x + y – 5 = 0 thành đường thẳng có phương trình:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Biểu thức tọa độ của phép quay tâm I(x0; y0), góc quay φ là
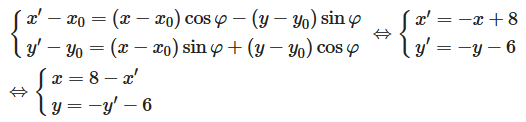
Thay vào phương trình đường thẳng d ta được:
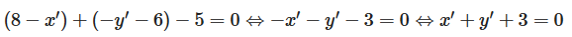
Vậy ta chọn đáp án C.
Câu 7:
Giải phương trình:
a) \[sinx + cosx = \sqrt 2 sin\left( {x + \frac{\pi }{4}} \right)\];
b) \[\sqrt 3 sinx + cosx = 2sin\left( {x + \frac{\pi }{6}} \right)\];
c) \[cosx - \sqrt 3 sinx = 2sin\left( {x + \frac{\pi }{4}} \right)\].
 Xem đáp án
Xem đáp án
a) Ta có
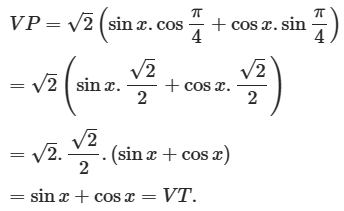
Vậy phương trình nghiệm đúng với mọi x.
b) Ta có
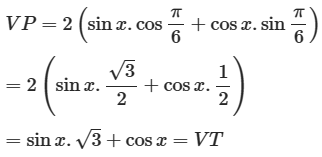
Vậy phương trình nghiệm đúng với mọi x.
c) Chia cả 2 vế cho 2 ta có
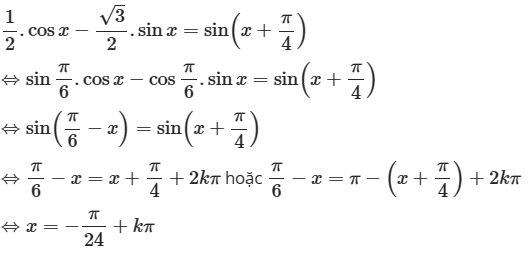
Vậy phương trình có nghiệm \(x = \frac{{ - \pi }}{{24}} + k\pi \left( {k \in \mathbb{Z}} \right)\).
Câu 8:
Cho tam giác ABC vuông tại A, đường cao AH. Biết diện tích tam giác ABH và ACH lần lượt là 54 cm2 và 96 cm2. Tính độ dài BC.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
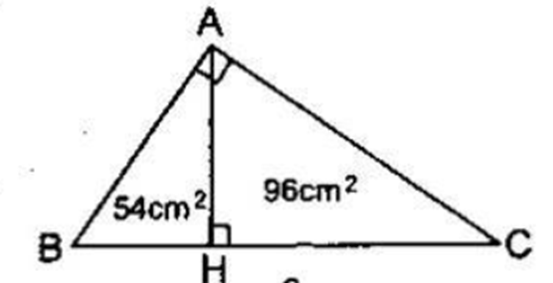
Xét tam giác ABC vuông tại A có AH ⊥ BC
Suy ra AH2 = BH . CH
Ta có \({S_{ABH}} = \frac{1}{2}AH.BH = 54\)
Suy ra AH . BH = 108
Ta có \({S_{ACH}} = \frac{1}{2}AH.CH = 96\)
Suy ra AH . CH = 192
Ta có AH . BH . AH . CH = 108 . 192
Hay AH4 = 20 736 = 124
Suy ra AH = 12 (cm)
Ta có \({S_{ABC}} = {S_{ABH}} + {S_{ACH}} = 54 + 96 = 150\)
Mà \({S_{ABC}} = \frac{1}{2}AH.BC\)
Suy ra \(\frac{1}{2}.12.BC = 150 \Rightarrow BC = 25\left( {cm} \right)\)
Vậy ta chọn đáp án B.
Câu 9:
Một tam giác có độ dài 3 cạnh là 13, 14, 15. Tính diện tích của tam giác đó.
 Xem đáp án
Xem đáp án
Nửa chu vi tam giác đó là
p = (13 + 14 + 15) : 2 = 21
Diện tích tam giác đó là
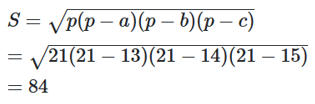
Vậy diện tích tam giác đó bằng 84.
Câu 10:
Tìm số lớn nhất có 3 chữ số biết, khi chia cho 75 thì thương và số dư bằng nhau.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là abc (a ≠ 0 ; a, b, c là các chữ số)
Gọi k là thương hay số dư với k ∈ ℕ*
Ta có abc : 75 = k dư k
Hay abc = 75k + k
Suy ra abc = 76k
Vì abc lớn nhất nên 76k lớn nhất có 3 chữ số, 1000 : 75 = 13,333
Suy ra k = 13
Khi đó abc = 76k = 988
Vậy số cần tìm là 988.
Câu 11:
Tìm số tự nhiên x biết: x chia hết cho 14 và 140 < x < 156.
 Xem đáp án
Xem đáp án
Vì x ⋮ 14 (x ∈ ℕ)
Nên x ∈ B(14)
Suy ra x ∈ {0; 14; 28; 42; 56; 70; 84; 98; 112; 126; 140; 154; 168; ...}
Mà 140 < x < 156
Suy ra x = 154
Vậy x = 154.
Câu 12:
Tam giác ABC vuông tại A, gọi I là giao điểm của các đường phân giác.
a) Biết AB = 5, IC = 6. Tính BC.
b) Biết \(IB = \sqrt 5 ,IC = \sqrt {10} \).Tính độ dài AB, AC.
 Xem đáp án
Xem đáp án
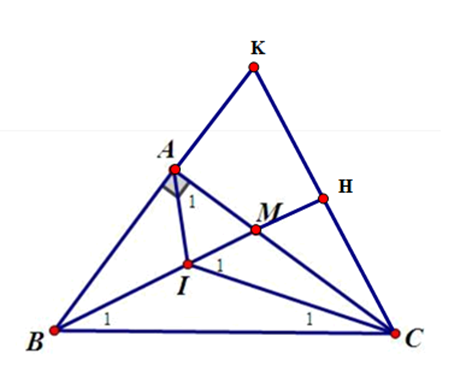
a) Vì tam giác ABC vuông tại A nên \(\widehat {ABC} + \widehat {ACB} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Vì AI là phân giác của góc BAC nên \(\widehat {{A_1}} = \frac{{\widehat {BAC}}}{2} = \frac{{90^\circ }}{2} = 45^\circ \)
Vì BI là phân giác của góc ABC nên \(\widehat {{B_1}} = \frac{{\widehat {ABC}}}{2}\)
Vì CI là phân giác của góc ACB nên \(\widehat {{C_1}} = \frac{{\widehat {ACB}}}{2}\)
Gọi giao điểm của BI và AC là M.
Vì \(\widehat {{I_1}}\) là góc ngoài của tam giác BIC
Nên \(\widehat {{I_1}} = \widehat {{B_1}} + \widehat {{C_1}} = \frac{{\widehat {ABC}}}{2} + \frac{{\widehat {ACB}}}{2} = \frac{{\widehat {ABC} + \widehat {ACB}}}{2} = \frac{{90^\circ }}{2} = 45^\circ \)
Xét DICM và DACI có
\(\widehat {{A_1}} = \widehat {{I_1}}\left( { = 45^\circ } \right)\);
\(\widehat {IC{\rm{A}}}\) là góc chung
Do đó (g.g)
Suy ra \(\frac{{IC}}{{AC}} = \frac{{CM}}{{CI}}\) (tỉ số đồng dạng)
Hay CI2 = CM . AC, mà IC = 6 nên CM . AC = 36
Suy ra \(CM = \frac{{36}}{{AC}}\).
Do BM là tia phân giác của \(\widehat {ABC}\) nên ta có
\(\frac{{CB}}{{AB}} = \frac{{CM}}{{MA}} \Leftrightarrow \frac{{BC}}{{BA + BC}} = \frac{{CM}}{{MA + CM}} \Leftrightarrow \frac{{BC}}{{5 + BC}} = \frac{{CM}}{{AC}}\)
Mà \(CM = \frac{{36}}{{AC}}\)
Suy ra \(\frac{{36}}{{A{C^2}}} = \frac{{BC}}{{BC + 5}} \Leftrightarrow \frac{{36}}{{B{C^2} - A{B^2}}} = \frac{{BC}}{{BC + 5}} \Leftrightarrow \frac{{36}}{{B{C^2} - 25}} = \frac{{BC}}{{BC + 5}}\)
\( \Leftrightarrow \frac{{36}}{{B{C^2} - 25}} = \frac{{BC\left( {BC - 5} \right)}}{{B{C^2} - 25}}\)
Suy ra BC(BC – 5) = 36
Hay BC2 – 5BC – 36 = 0
Suy ra BC = 9 (do BC > 0).
b) Kẻ CH ⊥ BI và CH cắt BA tại K.
Xét tam giác BCK có BH vừa là tia phân giác vừa là đường cao
Suy ra tam giác BCK cân tại B
Do đó BH là trung tuyến và BK = BC
Hay \[CH = HK = \frac{1}{2}CK\]
Đặt BC = x
Ta có AK = BK – AB = BC – AB = x – AB
Ta có: \(\widehat {ABM} = \widehat {HCM}\) (cùng phụ với \(\widehat {BKC}\))
Mà \(\widehat {ABM} = \frac{1}{2}\widehat {ABC}\) nên \(\widehat {HCM} = \frac{1}{2}\widehat {ABC}\)
Ta có \(\widehat {HCI} = \widehat {HCM} + \widehat {MCI} = \frac{1}{2}\widehat {ABC} + \frac{1}{2}\widehat {ACB} = \frac{1}{2}.90^\circ = 45^\circ \)
Xét tam giác ICH vuông ở H có
\(\widehat {HIC} + \widehat {HCI} = 90^\circ \) (trong một tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà \(\widehat {HCI} = 45^\circ \) nên \(\widehat {HIC} = 45^\circ \)
Suy ra \(\widehat {HCI} = \widehat {HIC}\)
Do đó tam giác HIC vuông ở H, nên HI = HC
Xét tam giác ICH vuông ở H có
IC2 = HI2 + HC2 (định lí Pytago)
Hay 10 = 2HI2 (do \(IC = \sqrt {10} \))
Suy ra \[HI = HC = \sqrt 5 \]
Ta có \[BH = BI + IH = \sqrt 5 + \sqrt 5 = 2\sqrt 5 \];
\[CK = 2CH = 2\sqrt 5 \]
Xét tam giác BCH vuông ở H có
BC2 = HB2 + HC2 (định lí Pytago)
Hay BC2 = 20 + 5
Suy ra BC = 5.
Xét tam giác BCA vuông ở A có
BC2 = AB2 + AC2 (định lí Pytago)
Hay 52 = AB2 + AC2 = 25
Xét tam giác AKC vuông ở A có
KC2 = AK2 + AC2 (định lí Pytago)
⇔ 20 = (BC – AB)2 + AC2
⇔ 20 = (5 – AB)2 + AC2
⇔ 20 = 25 – 10AB + AB2 + AC2
⇔ 20 = 25 – 10AB + 25
⇔ AB = 3
Khi đó \(AC = \sqrt {{5^2} - {3^2}} = 4\)
Vậy AB = 3, AC = 4.
Câu 13:
Trong kì thi đánh giá năng lực lần I năm học 2018 – 2019 của trường THPT Triệu Quang Phục, kết quả có 86 thí sinh đạt điểm giỏi môn Toán, 61 thí sinh đạt điểm giỏi môn Vật Lí và 76 thí sinh đạt điểm giỏi môn Hóa Học, 45 thí sinh đạt điểm giỏi cả hai môn Toán và Vật Lí, 21 thí sinh đạt điểm giỏi cả hai môn Vật Lí và Hóa Học, 32 thí sinh đạt điểm giỏi cả hai môn Toán và Hóa Học, 18 thí sinh đạt điểm giỏi cả ba môn Toán, Vật Lí và Hóa Học. Có 782 thí sinh mà cả ba môn đều không điểm giỏi. Hỏi trường THPT Triệu Quang Phục có bao nhiêu thí sinh tham dự kì thi đánh giá năng lực lần I năm học 2018 –2019?
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Ta biểu diễn các tập hợp như trong biểu đồ: Thí sinh đạt điểm giỏi môn Toán được biểu diễn màu trắng, Thí sinh đạt điểm giỏi môn Vật Lý được biểu diễn màu xanh. Thí sinh đạt điểm giỏi môn Hóa được biểu diễn màu hồng. Mỗi tập hợp nhỏ bên trong gọi tên như trong hình.
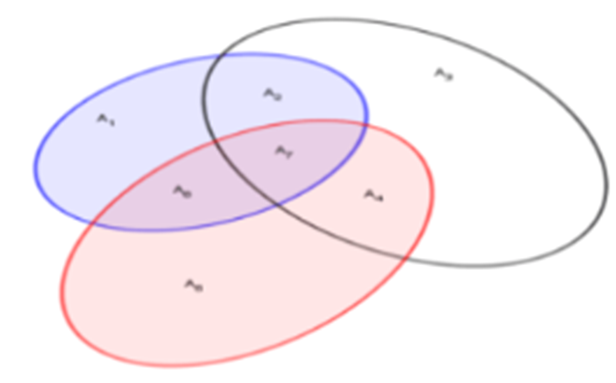
Ta có số thí sinh đạt điểm giỏi cả ba môn Toán, Vật Lí và Hóa Học là
n(A7) = 18
45 thí sinh đạt điểm giỏi cả hai môn Toán và Vật Lí ta được
n(A7) + n(A2) = 45
32 thí sinh đạt điểm giỏi cả hai môn Toán và Hóa Học ta được
n(A7) + n(A4) = 32
21 thí sinh đạt điểm giỏi cả hai môn Vật Lí và Hóa Học ta được
n(A7) + n(A6) = 21
Số thí sinh đạt điểm giỏi chỉ hai môn là
n(A6) + n(A4) + n(A2) = n(A7) + n(A2) + n(A7) + n(A4) + n(A7) + n(A6) – 3n(A7)
= 45 + 32 + 21 – 3 . 18 = 44
86 thí sinh đạt điểm giỏi môn Toán ta được
n(A3) + n(A4) + n(A2) + n(A7) = 86
61 thí sinh đạt điểm giỏi môn Vật Lí ta được
n(A1) + n(A6) + n(A2) + n(A7) = 61
76 thí sinh đạt điểm giỏi môn Hóa Học ta được
n(A4) + n(A6) + n(A5) + n(A7) = 76
Số thí sinh đạt điểm giỏi chỉ một môn là
n(A1) + n(A3) + n(A5)
= 86 + 61 + 76 – 3n(A7) – 2[n(A6) + n(A4) + n(A2)]
= 86 + 61 + 76 – 3 . 18 – 2 . 44 = 81
Số thí sinh đạt điểm giỏi gồm
n(A1) + n(A2) + n(A3) + n(A4) + n(A5) + n(A6) + n(A7)
= [n(A1) + n(A3) + n(A5)] + [n(A6) + n(A4) + n(A2)] + n(A7)
= 81 + 44 + 18 = 143
Trường THPT Triệu Quang Phục có số thí sinh tham dự kì thi đánh giá năng lực lần I
năm học 2018 – 2019 bao gồm số thí sinh đạt điểm giỏi và số thí sinh không đạt điểm giỏi nên bằng: 782 + 143 = 925 (thí sinh)
Vậy ta chọn đáp án C.
Câu 14:
Tìm các số tự nhiên x biết
a) x thuộc B(8) và x ≥ 30.
b) x chia hết cho 9 và x < 40.
c) x chia hết cho 6, x chia hết cho 21 và x < 200.
d) x chia hết cho 5, x chia hết 7, x chia hết cho 8 và ≥ 500.
e) 150 chia hết cho x , 120 chia hết cho x và x lớn nhất.
 Xem đáp án
Xem đáp án
a) x thuộc B(8) và x ≥ 30
Ta có: x ∈ B(8) = {0; 8; 16; 24; 32; 40; 48;...}
Mà x ≥ 30
Suy ra x = {32; 40; 48; ...}
b) x chia hết cho 9 và x < 40
Ta có x ⋮ 9
Nên x ∈ B(9) = {0; 9; 18; 27; 36; 45; 54;...}
Mà x < 40
Suy ra x = {0; 9; 18; 27; 36}
c) x chia hết cho 6 , x chia hết cho 21 và x < 200
Do x chia hết cho 6, 21 nên x ∈ BC(6; 21)
Ta có 6 = 2 x 3, 21 = 3 x 7
Suy ra BCNN(6; 21) = 2 x 3 x 7 = 42
Do đó BC(6; 21) = {0; 42; 84; 126; 168; 210; 252; ...}
Mà x < 200
Suy ra x = {0; 42; 84; 126; 168}
d) x chia hết cho 5, x chia hết 7, x chia hết cho 8 và ≥ 500
Do x chia hết cho 5, 7, 8 nên x ∈ BC(5; 7; 8)
Ta có: 5 = 5; 7 = 7; 8 = 23
Suy ra BCNN(5; 7; 8)= 23 x 5 x 7 = 280
Do đó BC(5; 7; 8) = {0; 280; 560; 840; 1120;...}
Mà x ≥ 500
Suy ra x={560; 840; 1120;...}
e) 150 chia hết cho x , 120 chia hết cho x và x lớn nhất
Ta có: 150 ⋮ x; 120 ⋮ x nên x ∈ ƯC(150; 120)
Phân tích: 150 = 2 x 3 x 52 ; 120 = 23 x 3 x 5
Suy ra ƯC(150; 120) = {2; 3; 5; 6; 10; 15; 30}
Mà x lớn nhất suy ra x = 30
Câu 15:
Tìm x, biết: x2 – 9 = 0.
 Xem đáp án
Xem đáp án
Ta có x2 – 9 = 0
⇔ (x – 3)(x + 3) = 0
⇔ \(\left[ \begin{array}{l}x - 3 = 0\\x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 3\end{array} \right.\)
Vậy x = 3 hoặc x = – 3.
Câu 16:
Giải phương trình: 2sin2 x – sinx – 1 = 0.
 Xem đáp án
Xem đáp án
Ta có 2sin2 x – sinx – 1 = 0
⇔ (2sinx + 1)(sinx – 1) = 0
\( \Leftrightarrow \left[ \begin{array}{l}{\mathop{\rm s}\nolimits} {\rm{inx}} = 1\\{\mathop{\rm s}\nolimits} {\rm{inx}} = \frac{{ - 1}}{2}\end{array} \right.\)
\[ \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = \frac{\pi }{2} + k2\pi \\{\rm{x}} = \frac{{ - \pi }}{6} + k2\pi \\x = \frac{{7\pi }}{6} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]
Vậy phương trình có nghiệm \(x = \frac{\pi }{2} + k2\pi \), \(x = \frac{{ - \pi }}{6} + k2\pi \), \(x = \frac{{7\pi }}{6} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
Câu 17:
Cho tứ giác ABCD.
Chứng minh rằng nếu \(\left| {\overrightarrow {A{\rm{D}}} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {DC} } \right|\) thì AC ⊥ BD.
 Xem đáp án
Xem đáp án
Ta có:
• \(\overrightarrow {A{\rm{D}}} + \overrightarrow {BC} = \left( {\overrightarrow {AC} + \overrightarrow {CD} } \right) + \left( {\overrightarrow {BD} + \overrightarrow {DC} } \right)\)
\( = \overrightarrow {AC} + \overrightarrow {BD} + \left( {\overrightarrow {CD} + \overrightarrow {DC} } \right) = \overrightarrow {AC} + \overrightarrow {BD} \)
• \(\overrightarrow {AB} + \overrightarrow {DC} = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {BC} } \right)\)
\( = \overrightarrow {AC} + \overrightarrow {DB} + \left( {\overrightarrow {CB} + \overrightarrow {BC} } \right) = \overrightarrow {AC} + \overrightarrow {DB} \)
Theo bài: \(\left| {\overrightarrow {A{\rm{D}}} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {DC} } \right|\)
\[ \Leftrightarrow \left| {\overrightarrow {AC} + \overrightarrow {BD} } \right| = \left| {\overrightarrow {AC} + \overrightarrow {DB} } \right|\]
\[ \Leftrightarrow {\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right|^2} = {\left| {\overrightarrow {AC} + \overrightarrow {DB} } \right|^2}\]
\[ \Leftrightarrow {\overrightarrow {AC} ^2} + 2\overrightarrow {AC} .\overrightarrow {BD} + {\overrightarrow {BD} ^2} = {\overrightarrow {AC} ^2} + 2\overrightarrow {AC} .\overrightarrow {DB} + {\overrightarrow {DB} ^2}\]
\[ \Leftrightarrow 2\overrightarrow {AC} .\overrightarrow {BD} + {\overrightarrow {BD} ^2} = - 2\overrightarrow {AC} .\overrightarrow {BD} + {\overrightarrow {BD} ^2}\]
\[ \Leftrightarrow 4\overrightarrow {AC} .\overrightarrow {BD} = 0\]
\[ \Leftrightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0\]
\[ \Leftrightarrow \overrightarrow {AC} \bot \overrightarrow {BD} \]
Suy ra AC ⊥ BD.
Câu 18:
Tam giác A(1; 3), B(5; – 1) có AB = 3, AC = 6, \(\widehat {BAC} = 60^\circ \). Tính độ dài đường cao ha của tam giác
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Áp dụng định lý hàm số cosin ta có
BC2 = AB2 + AC2 – 2AB . AC . cos A = 32 + 62 – 2 . 3 . 6 . cos60° = 27
Suy ra \(BC = 3\sqrt 3 \)
Ta có \({S_{ABC}} = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.3.6.\sin 60^\circ = \frac{{9\sqrt 3 }}{2}\)
Mà \({S_{ABC}} = \frac{1}{2}BC.{h_a}\)
Suy ra \({h_a} = \frac{{2{\rm{S}}}}{{BC}} = \frac{{9\sqrt 3 }}{{3\sqrt 3 }} = 3\)
Vậy ta chọn đáp án C.
Câu 19:
Phương trình sin2x = m có nghiệm nếu
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Vì – 1 ≤ sin2x ≤ 1 nên phương trình có nghiệm khi – 1 ≤ m ≤ 1
Vậy ta chọn đáp án A.
Câu 20:
Chứng minh rằng trong tam giác ABC ta có các hệ thức:
sin A = sinB.cosC + sinC.cosB.
 Xem đáp án
Xem đáp án
Theo định lý sin ta có
\(\frac{a}{{\sin {\rm{A}}}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2{\rm{R}}\)
Suy ra a = 2R . sinA, b = 2R . sinB, c = 2R . sinC
Ta có a2 = a2
\[ \Leftrightarrow {a^2} = \frac{{{a^2} + {b^2} - {c^2}}}{2} + \frac{{{a^2} + {c^2} - {b^2}}}{2}\]
⇔ a2 = ab . cosC + ac . cosB
⇔ a = bcosC + ccosB
⇔ 2R . sinA = 2R . sinBcosC + 2R . sinC cosB
⇔ sin A = sinB.cosC + sinC.cosB
Vậy sin A = sinB.cosC + sinC.cosB.
Câu 21:
Rút gọn biểu thức \[{\rm{A}} = \sqrt {x + \sqrt {2{\rm{x}} - 1} } - \sqrt {x - \sqrt {2{\rm{x}} - 1} } \].
 Xem đáp án
Xem đáp án
Ta có:
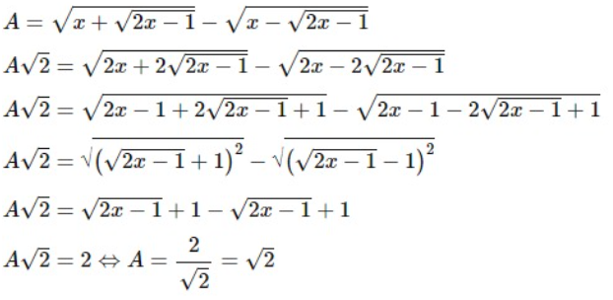
Vậy A = \(\sqrt 2 \).
Câu 22:
Cho tam giác ABC. Chứng minh rằng \(1 + \frac{r}{R} = \cos A + \cos B + \cos C\).
 Xem đáp án
Xem đáp án
Ta có
VP = cosA + cosB + cosC
=\(2\cos \frac{{A + B}}{2}.\cos \frac{{A - B}}{2} + \cos C\)
\( = 2\cos \frac{{180^\circ - C}}{2}.\cos \frac{{A - B}}{2} + \cos C\)
\[ = 2\cos \left( {90^\circ - \frac{C}{2}} \right).\cos \frac{{A - B}}{2} + \cos \left( {2.\frac{C}{2}} \right)\]
\[ = 2\sin \frac{C}{2}.\cos \frac{{A - B}}{2} + 1 - 2{\sin ^2}\frac{C}{2}\]
\[ = 2\sin \frac{C}{2}\left( {cos\frac{{A - B}}{2} - \sin \frac{C}{2}} \right) + 1\]
\[ = 2\sin \frac{C}{2}\left[ {cos\frac{{A - B}}{2} - \cos \left( {90^\circ - \frac{C}{2}} \right)} \right] + 1\]
\[ = 2\sin \frac{C}{2}\left[ {cos\frac{{A - B}}{2} - \cos \frac{{180^\circ - C}}{2}} \right] + 1\]
\[ = 2\sin \frac{C}{2}\left[ {cos\frac{{A - B}}{2} - \cos \frac{{A + B}}{2}} \right] + 1\]
\[ = 2\sin \frac{C}{2}\left( {2\sin \frac{A}{2}.\sin \frac{B}{2}} \right) + 1\]
\[ = 4\sin \frac{A}{2}.\sin \frac{B}{2}.\sin \frac{C}{2} + 1\] (1)
Ta có \(S = \frac{{abc}}{{4R}}\) và \(p = \frac{{a + b + c}}{2}\)
Suy ra \(r = \frac{S}{p} = \frac{{abc}}{{4{\rm{R}}{\rm{.}}\frac{{a + b + c}}{2}}}\)
\( = \frac{{\sin {\rm{A}}.2{\rm{R}}.\sin B.2{\rm{R}}.\sin C.2{\rm{R}}}}{{2{\rm{R}}\left( {\sin {\rm{A}}2{\rm{R}} + \sin B.2{\rm{R + }}\sin C.2{\rm{R}}} \right)}}\)
\( = \frac{{2{\rm{R}}\sin A.\sin B.\sin C}}{{\sin {\rm{A}} + \sin B + \sin C}}\)
Ta có: \(\sin A + \sin B + \sin C = 2\sin \frac{{A + B}}{2}.c{\rm{os}}\frac{{A - B}}{2} + \sin C\)
\( = 2\sin \frac{{180^\circ - C}}{2}.c{\rm{os}}\frac{{A - B}}{2} + 2\sin \frac{C}{2}.\cos \frac{C}{2}\)
\( = 2\sin \left( {90^\circ - \frac{C}{2}} \right).c{\rm{os}}\frac{{A - B}}{2} + 2\sin \frac{C}{2}.\cos \frac{C}{2}\)
\( = 2\cos \frac{C}{2}.c{\rm{os}}\frac{{A - B}}{2} + 2\sin \frac{C}{2}.\cos \frac{C}{2}\)
\( = 2\cos \frac{C}{2}.\left( {c{\rm{os}}\frac{{A - B}}{2} + \sin \frac{C}{2}} \right)\)
\( = 2\cos \frac{C}{2}.\left[ {c{\rm{os}}\frac{{A - B}}{2} + \cos \left( {90^\circ - \frac{C}{2}} \right)} \right]\)
\( = 2\cos \frac{C}{2}.\left[ {c{\rm{os}}\frac{{A - B}}{2} + \cos \frac{{180^\circ - C}}{2}} \right]\)
\( = 2\cos \frac{C}{2}.\left[ {c{\rm{os}}\frac{{A - B}}{2} + \cos \frac{{A + B}}{2}} \right]\)
\( = 2\cos \frac{C}{2}.\left( {2\cos \frac{A}{2}.\cos \frac{B}{2}} \right)\)
\( = 4\cos \frac{A}{2}.\cos \frac{B}{2}.\cos \frac{C}{2}\)
Suy ra
\(r = \frac{{2{\rm{R}}\sin A.\sin B.\sin C}}{{4\cos \frac{A}{2}.\cos \frac{B}{2}.\cos \frac{C}{2}}}\)
\(r = \frac{{2{\rm{R}}{\rm{.}}\left( {{\rm{2}}{\rm{.}}\sin \frac{A}{2}.\cos \frac{A}{2}} \right){\rm{.}}\left( {{\rm{2}}{\rm{.}}\sin \frac{B}{2}.\cos \frac{B}{2}} \right){\rm{.}}\left( {{\rm{2}}{\rm{.}}\sin \frac{C}{2}.\cos \frac{C}{2}} \right)}}{{4\cos \frac{A}{2}.\cos \frac{B}{2}.\cos \frac{C}{2}}}\)
\(r = 4R.\sin \frac{A}{2}.\sin \frac{B}{2}.\sin \frac{C}{2}\)
Suy ra \(1 + \frac{r}{R} = 1 + \frac{{4R.\sin \frac{A}{2}.\sin \frac{B}{2}.\sin \frac{C}{2}}}{R} = 1 + 4\sin \frac{A}{2}.\sin \frac{B}{2}.\sin \frac{C}{2}\) (2)
Từ (1) và (2) suy ra \(1 + \frac{r}{R} = \cos A + \cos B + \cos C\)
Vậy \(1 + \frac{r}{R} = \cos A + \cos B + \cos C\).
Câu 23:
Cho tam giác ABC vuông tại A, đường cao AH.
a) AB = 6 cm, BC = 10 cm. Tính AC, BH, HC, AH.
b) BH = 1 cm, AH = 2 cm. Tính HC, AC, BA, BC.
c) BH = 4 cm, HC = 9 cm. Tính BC, AB, AH, AC.
d) BH = 9 cm, AC = 20 cm. Tính HC, AH, AB, BC.
 Xem đáp án
Xem đáp án
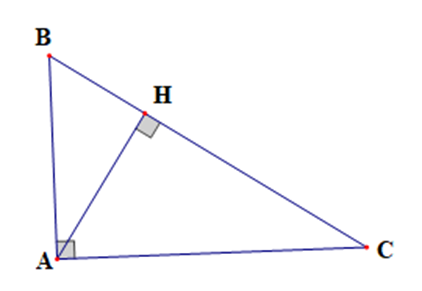
a) AB = 6 cm, BC = 10 cm. Tính AC, BH, HC, AH.
• Vì tam giác ABC vuông tại A nên BC2 = AB2 + AC2 (định lí Pytago)
Suy ra \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\) (cm)
• Xét DABC vuông tại A có AH là đường cao nên ta có:
AB2 = BH.BC, suy ra \(BH = \frac{{A{B^2}}}{{BC}} = \frac{{{6^2}}}{{10}} = 3,6\left( {cm} \right)\).
AC2 = CH.BC, suy ra \(CH = \frac{{A{C^2}}}{{BC}} = \frac{{{8^2}}}{{10}} = 6,4\left( {cm} \right)\).
AH . BC = AB . AC, suy ra \(AH = \frac{{AB.AC}}{{BC}} = \frac{{6.8}}{{10}} = 4,8\left( {cm} \right)\)
b) BH = 1 cm, AH = 2 cm. Tính HC, AC, BA, BC.
• Vì tam giác ABC vuông tại A có AH là đường cao nên:
AH2 = BH.CH, suy ra \[CH = \frac{{A{H^2}}}{{BH}} = \frac{{{2^2}}}{1} = 4\left( {cm} \right)\].
• Vì DACH vuông tại H nên AC2 = AH2 + CH2 (định lí Pytago)
Suy ra \(AC = \sqrt {{2^2} + {4^2}} = 2\sqrt 5 \left( {cm} \right)\).
• Vì DABH vuông tại H nên BA2 = HB2 + AH2 (định lí Pytago)
Suy ra \(AB = \sqrt {B{H^2} + A{H^2}} = \sqrt {{1^2} + {2^2}} = \sqrt 5 \) (cm)
• Xét DABC vuông tại A có AH là đường cao nên AB2 = BH . BC
Suy ra \(BC = \frac{{A{B^2}}}{{BH}} = \frac{{{{\left( {\sqrt 5 } \right)}^2}}}{1} = 5\left( {cm} \right)\).
c) BH = 4 cm, HC = 9 cm. Tính BC, AB, AH, AC.
• Ta có BC = BH + CH = 4 + 9 = 13 (cm).
• Xét DABC vuông tại A có AH là đường cao nên AB2 = BH . BC (hệ thức lượng trong tam giác vuông)
Suy ra \(AB = \sqrt {BH.BC} = \sqrt {4.13} = 2\sqrt {13} \left( {cm} \right)\)
• Xét DABC vuông tại A có AH là đường cao nên AH2 = BH.CH (hệ thức lượng trong tam giác vuông)
Suy ra \(AH = \sqrt {BH.CH} = \sqrt {4.9} = 6\left( {cm} \right)\).
• Vì DABC vuông tại A nên BC2 = AB2 + AC2 (định lí Pytago)
Suy ra \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{13}^2} - {{\left( {2\sqrt {13} } \right)}^2}} = 3\sqrt {13} \) (cm).
d) BH = 9 cm, AC = 20 cm. Tính HC, AH, AB, BC.
Xét DABC vuông tại A có AH là đường cao nên
• AC2 = CH . BC (hệ thức lượng trong tam giác vuông)
Û 202 = CH.(CH + BH)
Û 400 = CH.(CH + 9)
Û 400 = CH2 + 9CH
Û CH2 + 9CH – 400 = 0
Û CH = 16 cm (do CH > 0)
• AH2 = BH.CH = 9.16 = 144, suy ra AH = 12 (cm).
Xét DABH vuông tại H có AB2 = AH2 + BH2 (định lí Pytago)
Suy ra \(AB = \sqrt {A{H^2} + B{H^2}} = \sqrt {{{12}^2} + {9^2}} = \sqrt {225} = 15\left( {cm} \right)\)
Xét DABC vuông tại A nên BC2 = AB2 + AC2 (định lí Pytago)
Suy ra \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{15}^2} + {{20}^2}} = 25\) (cm)
Câu 24:
Cho \(B = \left( {1 - \frac{1}{2}} \right).\left( {1 - \frac{1}{3}} \right).\left( {1 - \frac{1}{4}} \right)....\left( {1 - \frac{1}{{20}}} \right)\).
So sánh B với \(\frac{1}{{21}}\).
 Xem đáp án
Xem đáp án
Ta có
\(B = \left( {1 - \frac{1}{2}} \right).\left( {1 - \frac{1}{3}} \right).\left( {1 - \frac{1}{4}} \right)....\left( {1 - \frac{1}{{20}}} \right)\)
\(B = \frac{1}{2}.\frac{2}{3}.\frac{3}{4}.....\frac{{19}}{{20}}\)
\(B = \frac{{1.2.3....19}}{{2.3.4....20}} = \frac{1}{{20}}\)
Vì 20 < 21 nên \(\frac{1}{{20}} > \frac{1}{{21}}\)
Vậy \(B > \frac{1}{{21}}\).
Câu 25:
Rút gọn biểu thức \[{\rm{A}} = \left( {3\sqrt 2 + \sqrt 6 } \right)\sqrt {6 - 3\sqrt 3 } \].
 Xem đáp án
Xem đáp án
Ta có \[{\rm{A}} = \left( {3\sqrt 2 + \sqrt 6 } \right)\sqrt {6 - 3\sqrt 3 } \]
\[{\rm{A}} = \sqrt 2 \left( {3 + \sqrt 3 } \right)\sqrt {6 - 3\sqrt 3 } \]
\[{\rm{A}} = \left( {3 + \sqrt 3 } \right)\sqrt {12 - 6\sqrt 3 } \]
\[{\rm{A}} = \left( {3 + \sqrt 3 } \right)\sqrt {9 - 6\sqrt 3 + 3} \]
\[{\rm{A = }}\left( {3 + \sqrt 3 } \right)\sqrt {{{\left( {3 - \sqrt 3 } \right)}^2}} \]
\[{\rm{A}} = \left( {3 + \sqrt 3 } \right)\left( {3 - \sqrt 3 } \right)\]
A = 9 – 3 = 6
Vậy A = 6.
Câu 26:
Cho tứ diện S.ABC. Gọi O là điểm thuộc miền trong của tam giác ABC. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh SA, SC sao cho MN không song song với AC. Tìm thiết diện do (MNO) cắt tứ diện S.ABC.
 Xem đáp án
Xem đáp án
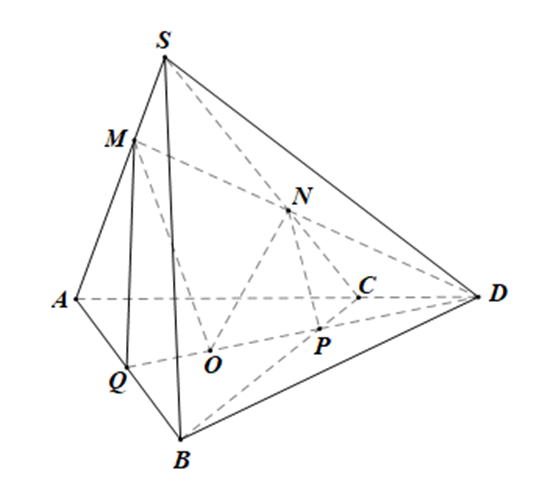
• (OMN) ∩ (SAC) = MN;
• Trong mp(SAC), gọi D = MN ∩ AC.
Trong mp(ABC), gọi P = BC ∩ OD.
Khi đó P ∈ OD ⊂ (OMN) và P ∈ (SBC), suy ra P = (OMN) ∩ (SBC)
Mà N = (OMN) ∩ (SBC), suy ra (OMN) ∩ (SBC) = NP.
• Do P ∈ BC, BC ⊂ (ABC) nên P ∈ (ABC)
Suy ra P = (OMN) ∩ (ABC)
Lại có O = (OMN) ∩ (ABC)
Suy ra (OMN) ∩ (ABC) = OP.
• Trong mp(ABC), gọi Q = OP ∩ AB.
Khi đó Q ∈ (OMN) và Q ∈ (ABC) nên Q = (OMN) ∩ (ABC)
Lại có M ∈ (OMN) và M ∈ (ABC) nên M = (OMN) ∩ (ABC)
Suy ra (OMN) ∩ (ABC) = QM.
Vậy thiết diện do (MNO) cắt tứ diện S.ABC là (MNPQ).
Câu 27:
Cho tam giác ABC có hb + hc = 2ha. Chứng minh rằng:
\(\frac{1}{{\sin B}} + \frac{1}{{\sin C}} = \frac{2}{{\sin {\rm{A}}}}\).
 Xem đáp án
Xem đáp án
Ta có \({S_{ABC}} = \frac{1}{2}{h_a}a = \frac{1}{2}{h_b}b = \frac{1}{2}{h_c}c\)
Suy ra \[{h_b} = \frac{{2{{\rm{S}}_{ABC}}}}{b},{h_c} = \frac{{2{{\rm{S}}_{ABC}}}}{c},{h_a} = \frac{{2{{\rm{S}}_{ABC}}}}{a}\]
Ta có hb + hc = 2ha
\( \Leftrightarrow \frac{{2{{\rm{S}}_{ABC}}}}{b} + \frac{{2{{\rm{S}}_{ABC}}}}{c} = \frac{{{\rm{4}}{{\rm{S}}_{ABC}}}}{a}\)
\( \Leftrightarrow \frac{1}{b} + \frac{1}{c} = \frac{2}{a}\)
Áp dụng định lí sin ta có
\(\frac{1}{{\sin {\rm{A}}}} + \frac{1}{{\sin B}} = \frac{{2R}}{b} + \frac{{2{\rm{R}}}}{c} = 2{\rm{R}}\left( {\frac{1}{b} + \frac{1}{c}} \right) = 2{\rm{R}}.\frac{2}{a} = \frac{2}{{\sin {\rm{A}}}}\)
Vậy \(\frac{1}{{\sin B}} + \frac{1}{{\sin C}} = \frac{2}{{\sin {\rm{A}}}}\).
Câu 28:
Hãy phân tích các đa thức sau thành nhân tử
a) 6x2 – 3xy;
b) x2 – y2 – 6x + 9.
 Xem đáp án
Xem đáp án
a) 6x2 – 3xy = 3x(2x – y)
b) x2 – y2 – 6x + 9 = (x2 – 6x + 9) – y2
= (x – 3)2 – y2
= (x – 3 – y)(x – 3 + y)
Câu 29:
giải phương trình:
a) 2sin2x + sinx = 0;
b) sinx + cos3x = 0;
c) sinx + 2cosx = 0;
d) 2sin2 3x = 1;
e) cos2x = 2cosx – 1.
 Xem đáp án
Xem đáp án
a) 2sin2x + sinx = 0
⇔ 4sinx.cosx + sinx = 0
⇔ sinx(4cosx + 1) = 0
\( \Leftrightarrow \left[ \begin{array}{l}{\mathop{\rm s}\nolimits} {\rm{inx}} = 0\\{\rm{cosx = }}\frac{{ - 1}}{4}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = k\pi \\{\rm{x = ar}}cc{\rm{os }}\frac{{ - 1}}{4} + k2\pi \\x = - {\rm{ar}}cc{\rm{os }}\frac{{ - 1}}{4} + k2\pi \end{array} \right.\) (k ∈ ℤ)
b) sinx + cos3x = 0
\[ \Leftrightarrow sinx + sin\left( {\frac{\pi }{2} - 3x} \right) = 0\]
\[ \Leftrightarrow sinx = sin\left( {3x--\frac{\pi }{2}} \right)\]
\( \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = 3{\rm{x}} - \frac{\pi }{2} + k2\pi \\{\rm{x = }}\pi - 3{\rm{x}} - \frac{\pi }{2} + k2\pi {\rm{ }}\end{array} \right.\)(k ∈ ℤ)
\( \Leftrightarrow \left[ \begin{array}{l} - 2{\rm{x}} = - \frac{\pi }{2} + k2\pi \\{\rm{4x = }}\frac{{3\pi }}{2} + k2\pi {\rm{ }}\end{array} \right.\)(k ∈ ℤ)
\( \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = \frac{\pi }{4} + k\pi \\{\rm{x = }}\frac{{3\pi }}{8} + \frac{{k\pi }}{2}{\rm{ }}\end{array} \right.\)(k ∈ ℤ)
c) sinx + 2cosx = 0
⇔ sinx = – 2cosx
\( \Leftrightarrow \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}{{{\rm{cosx}}}} = \frac{{ - 2co{\rm{sx}}}}{{\cos x}}\)
⇔ tanx = – 2
⇔ x = arctan(– 2) + kπ (k ∈ ℤ)
d) 2sin2 3x = 1
\[ \Leftrightarrow si{n^2}3x = \frac{1}{2}\]
\( \Leftrightarrow \left[ \begin{array}{l}\sin 3{\rm{x}} = \frac{1}{{\sqrt 2 }}\\\sin 3{\rm{x}} = - \frac{1}{{\sqrt 2 }}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}\sin 3{\rm{x}} = \sin \frac{\pi }{4}\\\sin 3{\rm{x}} = \sin \frac{{ - \pi }}{4}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}3{\rm{x}} = \frac{\pi }{4} + k2\pi \\3{\rm{x}} = \pi - \frac{\pi }{4} + k2\pi \\3{\rm{x}} = \frac{{ - \pi }}{4} + k2\pi \\3{\rm{x}} = \pi + \frac{\pi }{4} + k2\pi \end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = \frac{\pi }{{12}} + \frac{{k2\pi }}{3}\\{\rm{x}} = \frac{\pi }{4} + \frac{{k2\pi }}{3}\\{\rm{x}} = \frac{{ - \pi }}{{12}} + \frac{{k2\pi }}{3}\\{\rm{x}} = \frac{{5\pi }}{{12}} + \frac{{k2\pi }}{3}\end{array} \right.\) (k ∈ ℤ)
e) cos2x = 2cosx – 1
⇔ 2cos2x – 1 = 2cosx – 1
⇔ 2cos2x – 2cosx = 0
⇔ 2cosx(cosx – 1) = 0
\( \Leftrightarrow \left[ \begin{array}{l}{\rm{cosx = 0}}\\{\rm{cosx = 1}}\end{array} \right.\)
\[ \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = \frac{\pi }{2} + k\pi \\{\rm{x = }}k2\pi {\rm{ }}\end{array} \right.\] (k ∈ ℤ)
Câu 30:
Rút gọn
A = \(\sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} + \sqrt {{{\left( {\sqrt 5 - 3} \right)}^2}} \);
B = \(\sqrt {7 - 2\sqrt {10} } - \sqrt {6 - 2\sqrt 5 } \);
C = \(\left( {4 + \sqrt {15} } \right)\left( {\sqrt {10} - \sqrt 6 } \right)\sqrt {4 - \sqrt {15} } \).
 Xem đáp án
Xem đáp án
Ta có
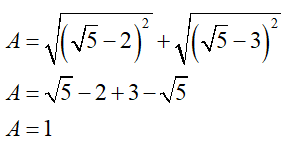
Ta có
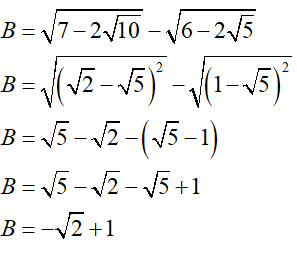
Ta có
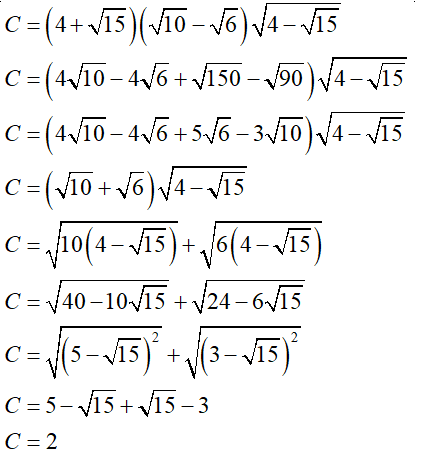
Câu 31:
Tìm số nghiệm thuộc đoạn [0; π] của phương trình sin2 x – cos2 3x = 0.
 Xem đáp án
Xem đáp án
Ta có sin2 x – cos2 3x = 0
\( \Leftrightarrow \frac{{1 - co{s^2}x}}{2} - \frac{{1 + cos6{\rm{x}}}}{2} = 0\)
⇔ cos2x + cos6x = 0
⇔ 2cos2x . cos4x = 0
\[ \Leftrightarrow \left[ \begin{array}{l}cos4{\rm{x}} = 0\\cos2{\rm{x}} = 0\end{array} \right.\]
\( \Leftrightarrow \left[ \begin{array}{l}4{\rm{x}} = \frac{\pi }{2} + k\pi \\2{\rm{x}} = \frac{\pi }{2} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = \frac{\pi }{8} + \frac{{k\pi }}{4}\\{\rm{x}} = \frac{\pi }{4} + \frac{{k\pi }}{2}\end{array} \right.\) (k ∈ ℤ)
+) Với \(x = \frac{\pi }{8} + \frac{{k\pi }}{4}\)
Vì 0 ≤ x ≤ π
Nên \(0 \le \frac{\pi }{8} + \frac{{k\pi }}{4} \le \pi \)
\[ \Leftrightarrow - \frac{\pi }{8} \le \frac{{k\pi }}{4} \le \pi - \frac{\pi }{8}\]
⇔ – 0,5 ≤ k ≤ 3,5
Mà k ∈ ℤ nên k ∈ {0; 1; 2; 3}
Khi đó \(x \in \left\{ {\frac{\pi }{8};\frac{{3\pi }}{8};\frac{{5\pi }}{8};\frac{{7\pi }}{8}} \right\}\)
+) Với \(x = \frac{\pi }{4} + \frac{{k\pi }}{2}\)
Vì 0 ≤ x ≤ π
Nên \(0 \le \frac{\pi }{4} + \frac{{k\pi }}{2} \le \pi \)
\( \Leftrightarrow - \frac{\pi }{4} \le \frac{{k\pi }}{2} \le \pi - \frac{\pi }{4}\)
⇔ – 0,5 ≤ k ≤ 1,5
Mà k ∈ ℤ nên k ∈ {0; 1}
Khi đó \(x \in \left\{ {\frac{\pi }{4};\frac{{3\pi }}{4}} \right\}\)
Vậy \(x \in \left\{ {\frac{\pi }{8};\frac{{3\pi }}{8};\frac{{5\pi }}{8};\frac{{7\pi }}{8};\frac{\pi }{4};\frac{{3\pi }}{4}} \right\}\).
Câu 32:
Điền >, <, = vào chỗ trống:
\(\frac{1}{4}\) giờ ... 40 phút;
\(\frac{1}{6}\)giờ ... \(\frac{1}{5}\)giờ;
\(\frac{1}{2}\)giờ ...\(\frac{1}{3}\)giờ.
 Xem đáp án
Xem đáp án
• Ta có \(\frac{1}{4}\) giờ = 15 phút nên \(\frac{1}{4}\) giờ < 40 phút;
• Ta có \(\frac{1}{5}\) giờ = 12 phút, \(\frac{1}{6}\) giờ = 10 phút nên \(\frac{1}{6}\)giờ < \(\frac{1}{5}\)giờ;
• Ta có \(\frac{1}{2}\) giờ = 30 phút, \(\frac{1}{3}\) giờ = 20 phút nên \(\frac{1}{2}\)giờ > \(\frac{1}{3}\)giờ.
Câu 33:
Tính nhanh 732 – 272.
 Xem đáp án
Xem đáp án
732 – 272
= (73 + 27)(73 – 27)
= 100 . 46
= 4 600
Vậy 732 – 272 = 4 600.
Câu 34:
Giải phương trình (2x + 1)4 = (2x + 1)6
 Xem đáp án
Xem đáp án
Ta có:
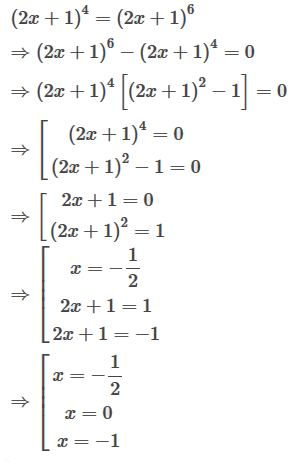
Vậy \[{\rm{x}} \in \left\{ { - 1;\frac{{ - 1}}{2};0} \right\}\].
Câu 36:
Trong mặt phẳng tọa độ Oxy, cho hình bình hành OABC với điểm A(– 2; 1), điểm B thuộc đường thẳng D: 2x – y – 5 = 0. Tìm quỹ tích đỉnh C.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì điểm B thuộc đường thẳng D: 2x – y – 5 = 0 nên B(xB; 2xB – 5)
Ta có \(\overrightarrow {OA} = \left( { - 2;1} \right)\)
Gọi C(xC; yC)
Suy ra \(\overrightarrow {CB} = \left( {{x_B}--{x_C};2{x_B} - 5 - {y_C}} \right)\)
Vì OABC là hình bình hành nên \(\overrightarrow {OA} = \overrightarrow {CB} \)
Suy ra \(\left\{ \begin{array}{l}{x_B} - {x_C} = - 2\\2{x_B} - 5 - {y_C} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = {x_C} - 2\\2{x_B} = 6 + {y_C}\end{array} \right.\)
Suy ra yC + 6 = 2(xC – 2)
Hay yc = 2xC – 10
Suy ra quỹ tích điểm C là đường thẳng y = 2x – 10
Hay 2x – y – 10 = 0
Vậy ta chọn đáp án A.
Câu 37:
Phương trình sin6 x + cos6 x + 3sinxcosx – m + 2 = 0 có nghiệm khi m thuộc [a; b] thì tích a . b bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Ta có
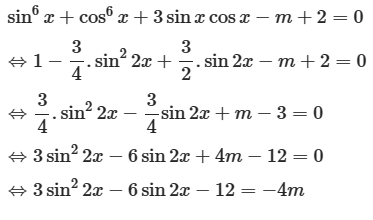
Đặt sin2 2x = t ( t ∈ [– 1; 1])
Suy ta 3t2 – 6t – 12 = – 4m (*)
Lập bảng biến thiên hàm số f(t) = 3t2 – 6t – 12 ta có
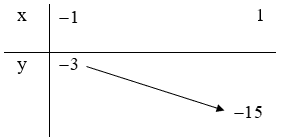
Suy ra phương trình (*) có nghiệm khi
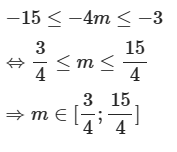
Khi đó \(a = \frac{3}{4},b = \frac{{15}}{4}\)
Ta có: \(ab = \frac{3}{4}.\frac{{15}}{4} = \frac{{45}}{{16}}\)
Vậy \(ab = \frac{{45}}{{16}}\).
Câu 38:
Có bao nhiêu giá trị nguyên của tham số m để phương trình
\[si{n^6}x + co{s^6}x + 3sinxcosx--\frac{m}{4} + 2 = 0\] có nghiệm thực?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có
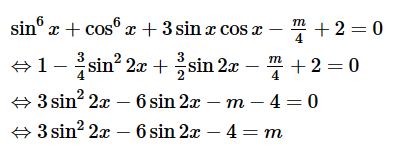
Đặt sin 2x = t (với t ∈ [– 1; 1])
Suy ta 3t2 – 6t – 4 = m
Xét sự biến thiên hàm số y = f(t) = 3t2 – 6t – 4 trong [– 1; 1] có
y’ = 6t – 6
y’ = 0 ⟺ 6t – 6 = 0 ⟺ t = 1
Ta có f(1) = – 7 và f(– 1) = 5
Suy ra phương trình có nghiệm khi – 7 ≤ m ≤ 5
Do đó các giá trị nguyên của m là {– 7; – 6; – 5; – 4; – 3; – 2; – 1; 0; 1; 2; 3; 4; 5}
Vậy ta chọn đáp án A.
Câu 39:
Phân tích đa thức thành nhân tử
a) (1 + x2)2 – 4x(1 – x2);
b) (x2 – 8)2 + 36.
 Xem đáp án
Xem đáp án
a) (1 + x2)2 – 4x(1 – x2)
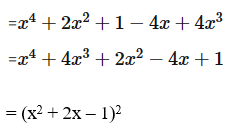
b) (x2 – 8)2 + 36 = x4 – 16x2 + 64 + 36 = x4 – 16x2 + 100
= x4 + 20x2 + 100 – 36x2
= (x2 + 10)2 – 36x2
= (x2 + 10 – 6x)(x2 + 10 + 6x).
Câu 41:
Số giá trị của a để hệ phương trình: xy + x + y = a + 1 và x2y + xy2 = a có nghiệm duy nhất.
 Xem đáp án
Xem đáp án
Đặt x + y = u, xy = v
Ta có hệ phương trình \(\left\{ \begin{array}{l}u + v = a + 1\\uv = a\end{array} \right.\)
Khi đó u, v là hai nghiệm của phương trình
X2 – (a + 1)X + a = 0
\( \Leftrightarrow \left[ \begin{array}{l}X = 1\\X = a\end{array} \right.\)
Suy ra \(\left[ \begin{array}{l}\left\{ \begin{array}{l}u = 1\\v = a\end{array} \right.\\\left\{ \begin{array}{l}u = a\\v = 1\end{array} \right.\end{array} \right.\)
+) Nếu \(\left\{ \begin{array}{l}u = 1\\v = a\end{array} \right.\)
Suy ra \(\left\{ \begin{array}{l}x + y = 1\\xy = a\end{array} \right.\)
Khi đó x, y là hai nghiệm của phương trình
M2 – M + a = 0 (1)
Để hệ phương trình có nghiệm duy nhất thì phương trình (1) có nghiệm kép
⇔ D = 0
⇔ 1 – 4a = 0
\( \Leftrightarrow a = \frac{1}{4}\)
+) Nếu \(\left\{ \begin{array}{l}u = a\\v = 1\end{array} \right.\)
Suy ra \(\left\{ \begin{array}{l}x + y = a\\xy = 1\end{array} \right.\)
Khi đó x, y là hai nghiệm của phương trình
N2 – aN + 1 = 0 (2)
Để hệ phương trình có nghiệm duy nhất thì phương trình (2) có nghiệm kép
⇔ D = 0
⇔ a2 – 4 = 0
\( \Leftrightarrow \left[ \begin{array}{l}a = 2\\a = - 2\end{array} \right.\)
Vậy \(a \in \left\{ {\frac{1}{4};2; - 2} \right\}\) .
Câu 42:
Cho tam giác ABC có \(\widehat A = 90^\circ \). Từ trung điểm E của cạnh AC kẻ EF vuông góc với BC. Nối AF với BE.
a) Chứng minh AF = BE . cosC.
b) Biết BC =10 cm, sinC = 0,6. Tính diện tích tứ giác ABFE.
c) AF và BE cắt nhau tại O. Tính sin góc AOB.
 Xem đáp án
Xem đáp án
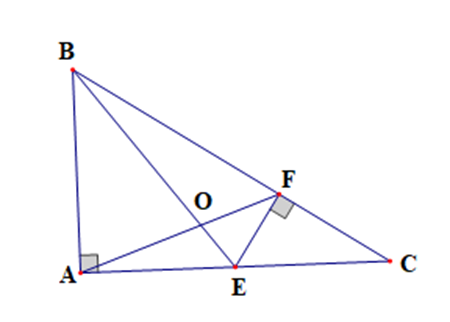
a) Xét tam giác CEF vuông ở F có \(\cos C = \frac{{CF}}{{CE}}\)
Xét tam giác CEF và tam giác CBA có
\(\widehat C\) là góc chung;
\(\widehat {BAC} = \widehat {{\rm{EF}}C} = 90^\circ \)
Suy ra (g.g)
Do đó \(\frac{{CF}}{{CE}} = \frac{{CA}}{{CB}}\)
Xét tam giác AFC và tam giác BEC có
\(\widehat C\) là góc chung;
\(\frac{{CF}}{{CE}} = \frac{{CA}}{{CB}}\) (chứng minh trên)
Suy ra (g.g)
Do đó \(\frac{{CF}}{{CE}} = \frac{{FA}}{{BE}}\)
Mà cosC = \(\frac{{CF}}{{CE}}\)
Suy ra AF = BE . cosC.
b) Vì tam giác ABC vuông tại A
Suy ra AB = BC . sinC = 10 . 0,6 = 6.
Xét tam giác ABC vuông tại A, theo định lí Pytago có
BC2 = AB2 + AC2
Suy ra \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)
Mà E là trung điểm AC nên AE = EC = 4
Vì tam giác FEC vuông tại F
Suy ra FE = EC . sinC = 4 . 0,6 = 2,4
Xét tam giác FEC vuông tại F, theo định lí Pytago có
EC2 = FE2 + FC2
Suy ra \(FC = \sqrt {E{C^2} - F{{\rm{E}}^2}} = \sqrt {{4^2} - 2,{4^2}} = 3,2\)
Khi đó BF = BC – FC = 10 – 3,2 = 6,8
Ta có SABFE = SABE + SBFE
\( = \frac{1}{2}AB.AE + \frac{1}{2}BF.FE\)
\( = \frac{1}{2}.6.4 + \frac{1}{2}.6,8.2,4 = 20,16\left( {c{m^2}} \right)\)
c) Ta có \(\frac{{CF}}{{CE}} = \frac{{FA}}{{BE}} = \frac{{3,2}}{4}\)
Suy ra AF = 0,8BE
Vì tam giác ABE vuông tại A nên
BE2 = AB2 + AE2
Hay BE2 = 62 + 42
suy ra \(BE = \sqrt {52} \)
Ta có \[{S_{ABFE}} = \frac{1}{2}AF.BE.\sin \widehat {AOB}\]
\( \Leftrightarrow 20,16 = \frac{1}{2}.0,8.\sqrt {52} .\sqrt {52} .\sin \widehat {AOB}\)
\( \Leftrightarrow \sin \widehat {AOB} = \frac{{20,16}}{{20,8}} = \frac{{63}}{{65}}\) .
Câu 43:
Cho tam giác ABC có AC = 7, AB = 5 và \(\cos A = \frac{3}{5}\). Tính BC, S, ha, R.
 Xem đáp án
Xem đáp án
Áp dụng định lí cosin ta có
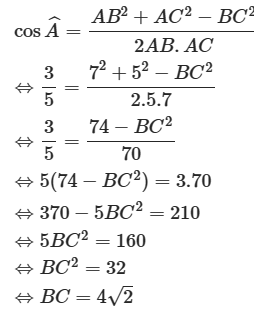
Vì 0° < \(\widehat A\) < 180° nên sinA > 0
Ta có sin2A + cos2A = 1
Suy ra
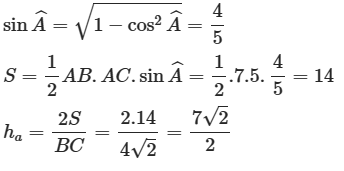
Áp dụng định lí sin ta có
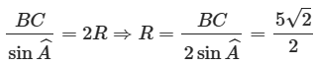
Câu 44:
Cho tam giác ABC, có AB = AC. AM là tia phân giác của góc A
a) Chứng minh DAMB = DAMC.
b) Chứng minh M là trung điểm của BC.
c) Cho biết Ax là tia phân giác góc ngoài của đỉnh A. Chứng minh Ax // BC.
 Xem đáp án
Xem đáp án
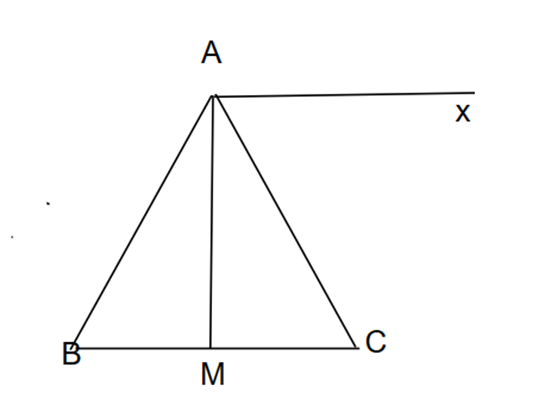
a) Vì AM là tia phân giác của góc BAC
Nên \(\widehat {BAM} = \widehat {CAM}\)
Xét DAMB và DAMC có
AB = AC (giả thiết)
\(\widehat {BAM} = \widehat {CAM}\) (chứng minh trên)
AM là cạnh chung
Suy ra DAMB = DAMC (c.g.c)
b) Vì DAMB = DAMC (chứng minh câu a)
Nên MB = MC (hai cạnh tương ứng)
Suy ra M là trung điểm của BC
c) Vì DAMB = DAMC (chứng minh câu a)
Nên \(\widehat {BMA} = \widehat {CMA}\) (hai góc tương ứng)
Mà \(\widehat {BMA} + \widehat {CMA} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {BMA} = \widehat {CMA} = 90^\circ \)
Hay AM ⊥ BC
Xét tam giác ABC có Ax là tia phân giác góc ngoài của đỉnh A
AM là phân giác góc trong tại đỉnh A
Suy ra AM ⊥ Ax
Mà AM ⊥ BC
Do đó Ax // BC (quan hệ từ vuông góc đến song song)
Vậy Ax // BC.
Câu 45:
Cho tam giác ABC vuông tại A, biết AC = 10 cm, \(\widehat C = 30^\circ \). Tính độ dài AB, CB.
 Xem đáp án
Xem đáp án
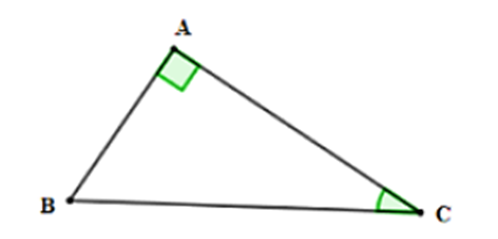
Xét tam giác ABC vuông tại A có
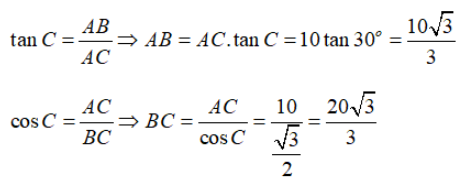
Vậy \(AB = \frac{{10\sqrt 3 }}{3}\left( {cm} \right),BC = \frac{{20\sqrt 3 }}{3}\left( {cm} \right)\).
Câu 46:
Có hàm số nào vừa chẵn, vừa lẻ không? Cho ví dụ.
 Xem đáp án
Xem đáp án
Có hàm số vừa chẵn vừa lẻ
Vì dụ hàm số y = f(x) = 0
Giải thích:
f(x) là hàm số chẵn khi f(– x) = f(x)
f(x) là hàm số lẻ khi f(– x) = – f(x)
Mà f(x) là hàm số vừa chẵn vừa lẻ
Suy ra f(x) = – f(x)
Hay f(x) = 0.
Câu 47:
Tìm m để phương trình sau có nghiệm:
m.sinx – 2m + 1 = 0 (*)
 Xem đáp án
Xem đáp án
+) Xét m = 0
Phương trình (*) ⇔ 1 = 0 (vô lý)
+) Xét m ≠ 0
Phương trình (*) \[ \Leftrightarrow \sin x = \frac{{2m - 1}}{m}\]
Vì – 1 ≤ sin x ≤ 1
Nên phương trình có nghiệm khi \( - 1 \le \frac{{2m - 1}}{m} \le 1\)
\( \Leftrightarrow \left\{ \begin{array}{l}\frac{{2m - 1}}{2} \ge - 1\\\frac{{2m - 1}}{2} \le 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{3m - 1}}{m} \ge 0\\\frac{{m - 1}}{m} \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m \ge \frac{1}{3}\\m \le 0\end{array} \right.\\0 \le m \le 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\\frac{1}{3} \le m \le 1\end{array} \right.\)
Mà m ≠ 0
Suy ra \(\frac{1}{3} \le m \le 1\)
Vậy \(\frac{1}{3} \le m \le 1\).
Câu 48:
Một người mua 5 m vải hết 100 000 đồng. Hỏi người đó mua 7,5 m vải cùng loại thì phải trả bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Mua 1 mét vải phải trả số tiền là:
100 000 : 5 = 20 000 ( đồng )
Mua 7,5 mét vải phải trả số tiền là:
20 000 × 7,5 = 150 000 ( đồng )
Vậy người đó mua 7,5 m vải cùng loại thì phải trả 150 000 đồng.
Câu 49:
Một hình chữ nhật có chiều dài gấp đôi chiều rộng. Tính chu vi hình chữ nhật đó, biết diện tích của nó là 32 cm2.
 Xem đáp án
Xem đáp án
Chia đôi nình chữ nhật theo chiều dài, ta được hai hình vuông có diện tích bằng nhau, cạnh hình vuông đúng bằng chiều rộng hình chữ nhật
Diện tích mỗi hình vuông mới là: 32 : 2 = 16 m2
Cạnh hình vuông hay chiều rộng hình chữ nhật là: 4 m.
Chiều dài hình chữ nhật là: 4 × 2 = 8 m.
Chu vi hình chữ nhật là: 24 m.
Vậy chu vi hình chữ nhật đó là 24 m.
Câu 50:
 Xem đáp án
Xem đáp án
Điều kiện xác định: x ≠ kπ, k ∈ ℤ
Ta có cotx = 0
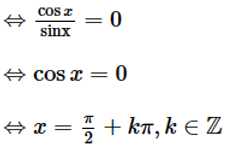
Vậy nghiệm của phương trình là \(x = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\).