- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 54)
-
11839 lượt thi
-
50 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Quả bưởi nặng 2 kg, quả dưa hấu nặng hơn quả bưởi \[\frac{2}{5}\] kg. Hỏi quả dưa hấu nặng bao bao nhiêu ki-lô-gam?
 Xem đáp án
Xem đáp án
Quả dưa hấu nặng số kg là:
\[2 + \frac{2}{5} = \frac{{10}}{5} + \frac{2}{5} = \frac{{12}}{5}\] (kg)
Đáp số: \[\frac{{12}}{5}\] kg.
Câu 2:
Viết số thập phân lớn nhất có năm chữ số khác nhau được viết bởi các chữ số 0; 1; 3; 5; 7 biết số thập phân đó có hai chữ số ở phần nguyên.
 Xem đáp án
Xem đáp án
Số lớn nhất có 5 chữ số được viết bởi các số đã cho là: 75 310.
Do có 2 chữ số ở phần nguyên nên số có dạng: 75,31.
Nhưng nếu số tận cùng trong phần thập phân là 00 thì dù viết vào hay không cũng không thay đổi giá trị nên số đó là: 75,301.
Vậy số cần tìm là 75,301.
Câu 3:
Tìm a, b, c thuộc ℕ sao cho 99a + 27b + 63c = 1 236 000.
 Xem đáp án
Xem đáp án
Ta có: 99; 27; 63 đều chia hết cho 9 nên 99a + 27b + 63c chia hết cho 9.
Mà 1 236 000 không chia hết cho 9 (do tổng các chữ số bằng 12 không chia hết cho 9).
Vậy không tồn tại a; b; c thuộc ℕ để 99a + 27b + 63c = 1 236 000.
Câu 4:
Tìm x, biết: x . 3 . 5 = 2,7
 Xem đáp án
Xem đáp án
x . 3 . 5 = 2,7
x . 15 = 2,7
x = 2,7 : 15
x = 0,18
Vậy x = 0,18
Câu 5:
 Xem đáp án
Xem đáp án
Vì |x – 3| ≥ 0; |y – 5| ≥ 0
Nên để |x – 3| + |y – 5| = 0 thì x – 3 = 0 và y – 5 = 0
• Với x – 3 = 0 thì x = 3.
• Với y – 5 = 0 thì y = 5.
Vậy x = 3, y = 5.
Câu 6:
Chứng minh 2 góc nhọn có cạnh tương ứng vuông góc thì bằng nhau.
 Xem đáp án
Xem đáp án
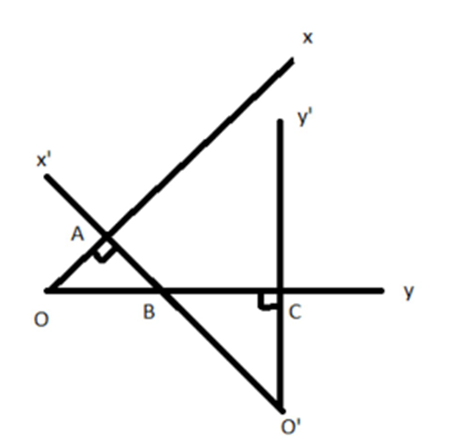
Ta có giả thiết 2 góc nhọn \[\widehat {xOy}\] và \[\widehat {x'O'y'}\] có các cặp cạnh tương ứng vuông góc: Ox ⊥ O’x’ và Oy ⊥ O’y’, cần chứng minh \[\widehat {xOy} = \widehat {x'O'y'}\].
Xét ΔOBA và ΔO’BC có
\[\widehat {OBA} = \widehat {O'BC}\] (đối đỉnh)
\[\widehat {OAB} = \widehat {O'CB} = 90^\circ \]
Do đó ΔOBA ᔕ ΔO’BC (g. g)
Suy ra \[\widehat {AOB} = \widehat {BO'C}\] hay \[\widehat {xOy} = \widehat {x'O'y'}\] (đpcm)
Câu 7:
Gà và vịt cân nặng 5,3 kg. Vịt và ngỗng cân nặng 6,9 kg. Ngỗng và gà cân nặng 5,8 kg. Hỏi mỗi con cân nặng bao nhiêu kg?
 Xem đáp án
Xem đáp án
Tổng số cân nặng của cả 3 con là:
(5,3 + 6,9 + 5,8) : 2 = 9 (kg)
Con gà cân nặng số kg là: 9 – 6,9 = 2,1 (kg)
Con vịt cân nặng số kg là: 5,3 – 2,1 = 3,2 (kg)
Con ngỗng cân nặng số kg là: 6,9 – 3,2 = 3,7 (kg)
Đáp số: Con gà: 2,1 kg;
Con vịt: 3,2 kg;
Con ngỗng: 3,7 kg.
Câu 8:
Khi nhân một số với 46, một học sinh đã sơ ý viết các tích riêng thẳng cột như trong phép cộng nên được kết quả là 1960. Tích đúng của phép nhân đó bằng?
 Xem đáp án
Xem đáp án
Gọi số cần tìm là a
Vì bạn đó đặt tích riêng thẳng cột nên ta có: 6 . a + 4 . a = 1960
(6 + 4) . a = 1960
10 . a = 1960
a = 196
Vậy tích đúng là: 196 . 46 = 9 016.
Câu 9:
Một vận động viên bắn súng, bắn ba viên đạn. Xác suất để trúng cả ba viên vòng 10 là 0,0008; xác suất đề một viên trúng vòng 8 là 0,15; xác suất để một viên trúng vòng dưới 8 là 0,4. Biết rằng các lần bắn là độc lập với nhau. Xác suất để vận động viên đó đạt ít nhất 28 điểm có giá trị gần bằng nhất với số nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xác suất để một viên trúng vòng 10 là: \[\sqrt[3]{{0,008}} \approx 0,0928\].
Xác suất để một viên trúng vòng 9 là:
1 − 0,4 − 0,0928 − 0,15 = 0,3572.
Các trường hợp xảy ra để thỏa mãn yêu cầu bài toán:
* Điểm ba lần bắn là 28 điểm, có 2 trường hợp: hai viên vòng 9 và một viên vòng 10 hoặc hai viên vòng 10 và một viên vòng 8.
Xác suất trong trường hợp này bằng:
\[\mathop P\nolimits_1 = C_3^2\,\,.\,\,{(0,3572)^2}\,.\,\,0,0928 + C_3^2\,\,.\,\,{(0,0928)^2}\,.\,\,0,15 \approx 0,0394\].
* Điểm ba lần bắn là 29 điểm, có 1 trường hợp: hai viên vòng 10 và một viên vòng 9. Xác suất trường hợp này bằng:
\[{P_2} = C_3^2\,\,.\,{(0,0928)^2}\,.\,\,0,3572 \approx 0,0092\].
* Điểm ba lần bắn là 30 điểm, có 1 trường hợp là cả ba viên vòng 10: Xác suất bằng 0,0008.
Vậy xác suất cần tìm bằng: P1 + P2 + 0,0008 = 0,00494.
Câu 10:
Chứng minh rằng nếu a chia hết cho m, b chia hết cho m thì a – b chia hết cho m.
 Xem đáp án
Xem đáp án
• Vì a ⁝ m nên ta có: a = m. q
• Vì b ⁝ m nên ta có: b = m. p
Do đó a - b = mq – mp = m(q – p) ⁝ m
Hay (a – b) ⁝ m
Câu 11:
Tìm tập hợp sau: B(4).
 Xem đáp án
Xem đáp án
Lấy 4 lần lượt nhân với các số 0; 1; 2; 3; 4; 5; … ta được: 0; 4; 8; 12; 16; 20; …
Khi đó B(4) = {0; 4; 8; 12; 16; 20; …}.
Câu 12:
Giải phương trình: x5 + x4 – x3 + x2 – x + 2 = 0.
 Xem đáp án
Xem đáp án
x5 + x4 - x3 + x2 – x + 2 = 0
⇔ x5 + 2x4 – x4 – 2x3 + x3 + 2x2 – x2 – 2x + x + 2 = 0
⇔ x4(x + 2) – x3(x + 2) + x2(x + 2) – x(x + 2) + (x + 2) = 0
⇔ (x + 2)(x4 – x3 + x2 – x + 1) = 0 (1)
Ta xét phương trình: x4 – x3 + x2 – x + 1 = 0 (2)
\[ \Leftrightarrow {\left( {{x^2} - \frac{1}{2}x} \right)^2} + {\left( {\frac{{\sqrt 3 }}{2}x - \frac{2}{{\sqrt 3 }}} \right)^2} + \frac{1}{3} = 0\]
Do \[{\left( {{x^2} - \frac{1}{2}x} \right)^2} + {\left( {\frac{{\sqrt 3 }}{2}x - \frac{2}{{\sqrt 3 }}} \right)^2} + \frac{1}{3} > 0\,\,\,\forall x\]
Nên phương trình (2) vô nghiệm
Suy ra phương trình (1) tương đương với:
x + 2 = 0 ⇔ x = –2
Vậy tập nghiệm của phương trình là S = {2}.
Câu 13:
Tổng của hai số bằng 10,45. Tìm hai số đó, biết rằng nếu số hạng thứ nhất cộng với 4 lần số hạng thứ hai thì được 22,45.
 Xem đáp án
Xem đáp án
Gọi số thứ nhất là a, số thứ hai là b
Ta có a + b = 10,45
a + 4b = 22,45
3b = 22,45 – 10,45
3b = 12,45
b = 4,15
Do đó a = 10,45 – 4,15 hay a = 6 ,3
Vậy số thứ nhất là 6,3; số thứ hai là 4,15.
Câu 14:
Giải phương trình: x . 3,9 + x . 0,1 = 2,7
 Xem đáp án
Xem đáp án
x . 3,9 + x . 0,1 = 2,7
⇔ x . (3,9 + 0,1) = 2,7
⇔ x = 2,7 : 4
⇔ x = 0,625
Vậy nghiệm của phương trình là x = 0,625.
Câu 15:
Tìm x, biết: \[\frac{{12,5}}{x} - \frac{{3,5}}{x} = 10\].
 Xem đáp án
Xem đáp án
Điều kiện: x ≠ 0
\[\frac{{12,5}}{x} - \frac{{3,5}}{x} = 10\]
\[\frac{{12,5 - 3,5}}{x} = 10\]
\[\frac{9}{x} = 10\]
x = 0,9
Vậy x = 0,9.
Câu 16:
Trên quãng đường AC có điểm B. Lúc 7 giờ, người thứ nhất đi từ A, người thứ hai đi từ B, cả 2 người cùng đến C lúc 10 giờ. Trên đường đi, người thứ hai gặp một chiếc xe lửa đi từ C đến A vào lúc 8 giờ 30 phút, người thứ nhất gặp chiếc xe lửa đó vào lúc 8 giờ 40 phút. Biết rằng AB dài 30 km và vận tốc xe lửa gấp đôi người thứ nhất. Hỏi xe lửa đi từ C lúc mấy giờ, và quãng đường AC dài bao nhiêu?
 Xem đáp án
Xem đáp án
Xe lửa gặp người thứ hai lúc 8 giờ 30 phút ở D, gặp người thứ nhất lúc 8 giờ 40 phút ở E.
Thời gian người thứ nhất đi EC là:
10 giờ – 8 giờ 40 phút = 80 phút
Thời gian xe lửa đi CE là:
80 : 2 = 40 (phút)
Xe lửa khởi hành từ C lúc là:
8 giờ 40 phút – 40 phút = 8 giờ
Thời gian xe lửa đi CD là:
8 giờ 30 phút – 8 giờ = 30 phút
Thời gian người thứ hai đi CD là:
10 giờ – 8 giờ 30 phút = 90 phút
Tỉ số vận tốc xe lửa và vận tốc người thứ hai là:
90 : 30 = 3 (lần)
Tỉ số vận tốc người thứ nhất và vận tốc người thứ hai là:
3 : 2= 1,5 (lần)
Quãng đường AC gấp rưỡi quãng đường BC nên quãng đường AC gấp ba AB, tức là:
30 . 3 = 90 (km)
Câu 17:
Tìm các số tự nhiên x sao cho: x ⋮ 15 và 0 < x < 40.
 Xem đáp án
Xem đáp án
Vì x ⋮ 15 nên x ∈ B(15) = {0; 15; 30; 45; 60; 75;…}.
Mà 0 < x < 40 nên x ∈ {15; 30}.
Câu 18:
Hai ông bà Brain cùng đến một buổi gặp mặt với 4 cặp vợ chồng khác nhân dịp năm mới. Nhóm người này tiến hành bắt tay nhau (không nhất thiết phải bắt tay với tất cả), nhưng không ai bắt tay với vợ/chồng của mình. Sau khi bắt tay, ông Brain đến hỏi từng người xem họ bắt tay với bao nhiêu người. Tất cả đều trả lời trung thực và thật ngạc nhiên là mỗi người lại đưa ra một con số khác nhau. Hỏi vợ chồng ông bà Brain bắt tay với bao nhiêu người?
 Xem đáp án
Xem đáp án
Chúng ta có 10 người trong nhóm và mỗi người có thể bắt tay với 0; 1; 2; 3; 4; 5; 6; 7 hoặc 8 người.
• Người bắt tay với 8 người sẽ bắt tay với tất cả mọi người ngoại trừ vợ/chồng của chính mình.
Vì mọi người khác bắt tay với ít nhất 1 người, điều đó có nghĩa là vợ/chồng của người này phải là người bắt tay với người trả lời là 0.
Câu trả lời của 8 và 0 được ghép nối, và đây là một cặp vợ chồng.
• Người bắt tay với 7 người, có nghĩa là bắt tay với tất cả mọi người ngoại trừ người vợ/chồng của chính họ và người trả lời 0.
Bây giờ mọi người khác, ngoại trừ bạn đời và người trả lời 0, phải bắt tay với ít nhất 2 người, nghĩa là vợ/chồng của người đó phải là người bắt tay với 1 người.
Câu trả lời của 7 và 1 được ghép nối, và đây là một cặp vợ chồng.
• Tương tự có thể được tiếp tục cho thấy rằng câu trả lời của 6 và 2 là một cặp vợ chồng, cũng như câu trả lời của 5 và 3.
Theo phương pháp loại trừ, câu trả lời còn lại phải là câu trả lời của bà Brain, người đã bắt tay với 4 người.
Ông Brain sẽ bắt tay với những người đưa ra câu trả lời 8, 7, 6 và 5 nên ông ấy không thể bắt tay với người trả lời 4 (vợ anh ta).
Câu trả lời 3 bắt tay với câu trả lời 8, 7 và 6; câu trả lời 2 bắt tay với câu trả lời 8 và 7; và câu trả lời của 1 bắt tay với câu trả lời là 8.
Câu trả lời 0 không bắt tay ai.
Do đó, ông Brain bắt tay với đúng 4 người, giống như vợ mình.
Vậy vợ chồng ông Brain mỗi người bắt tay với 4 người.
Câu 19:
Cho đường tròn tâm O đường kính 10 cm. Gọi H là trung điểm của dây AB. Tính độ dài đoạn OH, biết AB = 6 cm.
 Xem đáp án
Xem đáp án
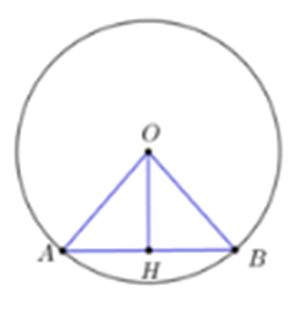
Xét đường tròn (O) ta có H là trung điểm của dây cung AB
Ta có OH ⊥ AB tại H (mối liên hệ giữa đường kính và dây cung).
Áp dụng định lý Py-ta-go cho tam giác OAH vuông tại H có:
OH2 = OA2 − AH2 = \[{R^2} - {\left( {\frac{{AB}}{2}} \right)^2}\]= 52 – 32 = 42
Do đó OH = 4 cm.
Câu 20:
Cho đường tròn (O; R), đường kính AB, dây cung DE. Tia DE cắt AB ở C. Biết góc \[\widehat {DOE} = 90^\circ \] và OC = 3R.
a) Tính độ dài CD và CE theo R.
b) Chứng minh: CD . CE = CA . CB.
 Xem đáp án
Xem đáp án
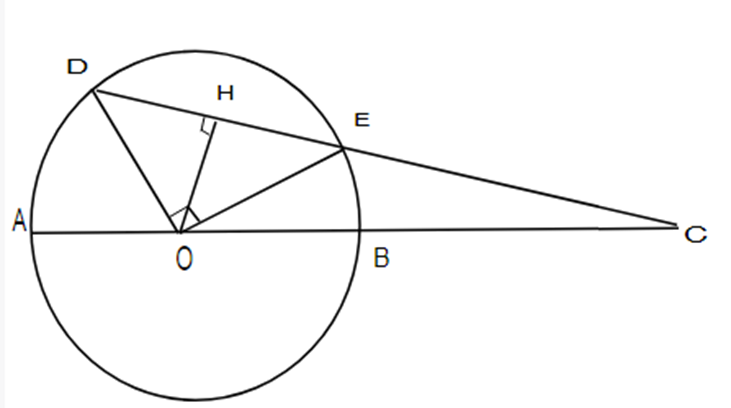
a) Xét ∆ODE có: \[\widehat {DOE} = 90^\circ \] và OD = OE = R
Do đó ∆ODE vuông cân tại O
• DE2 = OD2 + OE2 (Định lý Py-ta-go trong tam giác ODE vuông)
⇔ DE2 = 2R2
⇔ \[DE = \sqrt 2 R\]
• DE . OH = OD . OE (Hệ thức lượng trong ODE vuông)
⇔ \[\sqrt 2 R.OH = {R^2}\]
⇔ \[OH = \frac{{{R^2}}}{{\sqrt 2 R}} = \frac{R}{{\sqrt 2 }}\]
Xét ∆OHC có: \[\widehat {DHC} = 90^\circ \]
HC2 = DC2 – OH2
\[ \Leftrightarrow H{C^2} = 9{{\rm{R}}^2} - \frac{{{R^2}}}{2}\]
\[ \Leftrightarrow H{C^2} = \frac{{17{R^2}}}{2}\]
\[ \Rightarrow HC = \frac{{R\sqrt {34} }}{2}\] (cm) (1)
Mà \[DH = HE = \frac{{DE}}{2} = \frac{{\sqrt 2 R}}{2}\] (2)
Từ (1) và (2) suy ra DC = HC + DH
= \[\frac{{\sqrt {34} R}}{2} + \frac{{\sqrt 2 R}}{2} = \frac{{R\left( {\sqrt {34} + \sqrt 2 } \right)}}{2}\] (cm)
Ta có: CE = HC – HE
= \[\frac{{\sqrt {34} R}}{2} - \frac{{\sqrt 2 R}}{2} = \frac{{R\left( {\sqrt {34} - \sqrt 2 } \right)}}{2}\] (cm)
Vậy CD = \[\frac{{R\left( {\sqrt {34} + \sqrt 2 } \right)}}{2}\]
CE = \[\frac{{R\left( {\sqrt {34} - \sqrt 2 } \right)}}{2}\]
b) Ta có: DC . CE = AC . BC
⇔ \[\frac{{R\left( {\sqrt {34} + \sqrt 2 } \right)}}{2} \cdot \frac{{R\left( {\sqrt {34} - \sqrt 2 } \right)}}{2} = 4{\rm{R}} \cdot 2{\rm{R}}\]
⇔ 8R2 = 8R2
Vậy CD . CE = AC . BC
Câu 21:
Khi nhân một số có 5 chữ số với 1000, Hồng cho kết quả là số có 9 chữ số còn Hà cho kết quả là số có chữ số hàng trăm là 6. Hỏi kết quả của ai đúng?
 Xem đáp án
Xem đáp án
Gọi số có 5 chữ số đó là \[\overline {abc{\rm{d}}e} \].
Ta có: \[\overline {abc{\rm{d}}e} \cdot 1000 = \overline {abc{\rm{d}}e000} \].
Xét chữ số hàng trăm của \[\overline {abc{\rm{d}}e000} \] bằng 0.
Xét số \[\overline {abc{\rm{d}}e000} \] có 8 chữ số
Vậy kết quả của cả 2 bạn đều sai.
Câu 22:
Tìm số tự nhiên gồm ba chữ số. Biết rằng số đó chia hết cho 45 và khi viết nó theo thứ tự ngược lại, được 1 số mới gồm ba chữ số và chia hết cho 45.
 Xem đáp án
Xem đáp án
Gọi số có ba chữ số cần tìm là: \[\overline {abc} \] (a khác 0)
Theo đề ta có, số đó chia hết cho 45: \[\overline {abc} \] ⋮45 hay \[\overline {abc} \] ⋮ 5 và \[\overline {abc} \] ⋮ 9
Để \[\overline {abc} \] ⋮ 5 thì c là 0 hoặc 5 (1)
Để \[\overline {abc} \] ⋮ 9 thì a + b + c chia hết cho 9 (2)
Lại có: Khi viết thứ tự ngược lại ta được số có ba chữ số vẫn chia hết cho 45 nên ta có: \[\overline {cba} \] ⋮ 45 hay \[\overline {cba} \] ⋮ 5 và \[\overline {cba} \] ⋮ 9 (c khác 0)
Để \[\overline {cba} \] ⋮ 5 thì a là 0 hoặc 5 (3)
Để \[\overline {cba} \] ⋮ 9 thì c + b + a chia hết cho 9 (4)
Từ (1), (2), (3) và (4) ta có: \[\overline {5b5} \]
Mà 5 + b + 5 chia hết cho 9 nên b là 8.
Vậy số cần tìm là 585
Câu 23:
Thu gọn: S = 1 + x + x2 + x3 + …. + xn
 Xem đáp án
Xem đáp án
S = 1 + x + x2 + x3 + …. + xn
⇔ S = x0 + x1 + x2 + x3 + ...... + xn
⇒ xS = x1 + x2 + x3 + ...... + xn+1
⇒ xS – S = x1 + x2 + x3 + ...... + xn+1 - (x0 + x1 + x2 + x3 + ...... + xn)
⇔ S(x - 1) = x1 + x2 + x3 + ...... + xn+1 - x0 - x1 - x2 - x3 - …... - xn
⇔ S(x - 1) = xn+1 - x0
⇔ S(x-1) = xn+1 - 1
⇒ \[S = \frac{{{x^{n + 1}} - 1}}{{x - 1}}\]
Câu 24:
Một đơn vị bộ đội chuẩn bị một số gạo đủ cho 50 người ăn trong 10 ngày, 3 ngày sau được tăng thêm 20 người. Hỏi đơn vị cần chuẩn bị bao nhiêu suất gạo nữa để cả đơn vị đủ ăn trong những ngày sau đó? (Số gạo mỗi người ăn trong một ngày là một suất gạo)
 Xem đáp án
Xem đáp án
Số gạo đó đủ cho số người ăn trong 1 ngày là:
50 . 10 = 500 (người)
Số gạo đã ăn đủ cho số người ăn trong 1 ngày là:
50 . 3 = 150 (người)
Số gạo còn lại đủ cho số người ăn trong 1 ngày là:
500 – 150 = 350 (người)
Sau ngày thứ 3 thì có số người ăn là:
50 + 20 = 70 (người)
Số ngày còn lại là:
10 – 3 = 7 (ngày)
Số suất ăn cần là:
70 . 7 = 490 (suất)
Cần thêm số suất ăn là:
490 – 350 = 140 (suất)
Đáp số: 140 suất.
Câu 25:
Cho biết 3 người làm cỏ một cánh đồng hết 6 giờ. Hỏi 12 người (có cùng năng suất) làm cỏ cánh đồng đó hết bao nhiêu thời gian?
 Xem đáp án
Xem đáp án
Với cùng một cánh đồng nên số người làm cỏ hết cánh đồng đó và số giờ là hai đại lượng tỉ lệ nghịch.
Hệ số tỉ lệ bằng: 3 . 6 = 18
Gọi số giờ để 12 người làm cỏ hết cánh đồng là x (giờ)
Theo tính chất của đại lượng tỉ lệ nghịch ta có x . 12 = 18 suy ra x = 1,5
Vậy 12 người làm cỏ cánh đồng hết 1,5 giờ (1 giờ 30 phút)
Câu 26:
7a + 4b = 26. Tìm a và b.
 Xem đáp án
Xem đáp án
7a + 4b = 26
⇒ 7a = 26 - 4b ⇒ 7a = 2(13 - 2b)
⇒ 7a ⁝ 2 mà (2,7) = 1
⇒ a ⁝ 2
Vì 7a = 26 - 4b ⇒ 7a ≤ 26 ⇒ a < 4 ⇒ a = 0; 2
Xét a = 0 ⇒ 4b = 26 – 0 = 26 ⇒ b = \[\frac{{13}}{4}\] (vô lí)
Xét a = 2 ⇒ 4b = 26 – 2 . 7 = 26 – 14 = 12 ⇒ a = 3
Vậy a = 2, b = 3
Câu 27:
Cho đường tròn (O; R) và dây AB = 1,2R. Vẽ một tiếp tuyến song song với AB, cắt các tia OA, OB lần lượt tại E và F. Tính diện tích tam giác OEF theo R. (VJ)
 Xem đáp án
Xem đáp án

Kẻ \[OH \bot {\rm{EF}}\]tại H và cắt AB tại I
Suy ra \[OI \bot AB\] ( vì AB // EF)
Xét (O) có \[OI \bot AB\] tại I nên I là trung điểm AB (liên hệ giữa đường kính và dây cung)
Nên \[IA = IB = \frac{{AB}}{2} = 0,6{\rm{R}}\]
Lại có OA = R. Áp dụng định lý Pytago cho tam giác vuông OIA, ta có:
\[OI = \sqrt {O{A^2} - I{A^2}} = 0,8{\rm{R}}\]
Mà AI // EH nên \[\frac{{AI}}{{EH}} = \frac{{OI}}{{OH}} = \frac{{0,8{\rm{R}}}}{R}\]⇒ \[EH = \frac{{0,6{\rm{R}}}}{{0,8}} = 0,75{\rm{R}}\]
∆OEF cân tại O (vì \[\widehat E = \widehat F = \widehat {BAO} = \widehat {ABO}\])
Có \[OH \bot {\rm{EF}}\]nên H là trung điểm của EF
⇒ EF = 2EH = 1,5R
\[ \Rightarrow {S_{{\rm{EOF}}}} = \frac{{OH \cdot {\rm{EF}}}}{2} = 0,75{{\rm{R}}^2}\]
Vậy diện tích tam giác EOF là 0,75R2.
Câu 28:
 Xem đáp án
Xem đáp án
Áp dụng BĐT AM-GM ta có:
\[B = 2{\rm{a}} + 3b + \frac{6}{a} + \frac{{10}}{b} = a + b + a + 2b + \frac{6}{a} + \frac{{10}}{b}\]
\[ = 4 + a + \frac{4}{a} + 2b + \frac{8}{b} + \frac{2}{a} + \frac{2}{b}\]
\[ \ge 4 + 2\sqrt {a \cdot \frac{4}{a}} + 2 \cdot 2\sqrt {b \cdot \frac{4}{b}} + 2 \cdot \frac{4}{{a + b}}\]
= 4 + 2 . 2 + 2 . 2 . 2 + 2 . 1 = 4 + 2 . 2 + 2 . 2 . 2 + 2 . 1
= 4 + 4 + 8 + 2 = 18.
Nên GTNN của B là 18 đạt được khi a = b = 2.
Câu 29:
Cho các chữ số 3; 4; 5. Hãy viết các số thập phân gồm ba chữ số khác nhau trong đó, phần thập phân của các số đều có hai chữ số.
 Xem đáp án
Xem đáp án
Các số cần tìm là: 3,45; 3,54; 4,35; 4,53; 5,34; 5,43.
Câu 30:
Cho nửa đường tròn (O) đường kính AD. Trên nửa đường tròn lấy hai điểm B và C. Biết AB = BC = \[2\sqrt 5 \]cm, CD = 6cm. Tính bán kính đường tròn. (VJ)
 Xem đáp án
Xem đáp án
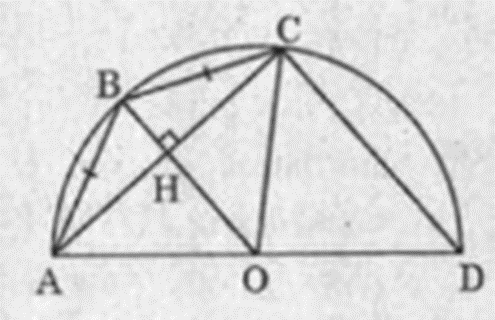
Dễ thấy OB là đường trung trực của AC nên \[OB \bot AC\] tại H và HA = HC
OH là đường trung bình của ∆ABC, ta có \[OH = \frac{1}{2}C{\rm{D}} = 3\]
• Xét ∆OHC vuông tại H, ta có:
HC2 = OC2 – OH2 = R2 – 9 (1)
• Xét ∆BHA vuông ở H, ta có:
HC2 = BC2 – BH2 = 20 – (R – 3)2 (2)
Từ (1) và (2) suy ra: R2 – 9 = 20 – (R – 3)2
⇔ R2 – 9 = 20 - R2 + 6R – 9
⇔ 2R2 – 6R – 20 = 0
⇔ (R – 5)(R + 2) = 0
⇔ R = 5 hoặc R = −2 (loại)
Vậy bán kính của đường tròn là 5 cm.
Câu 31:
Cho đường tròn (O) và dây cung AB của (O) không là đường kính. Gọi I là trung điểm của AB. Một đường thẳng thay đổi đi qua A cắt đường tròn tâm O bán kính OI tại P và Q.
a) Chứng minh rằng AP . AQ = AI2.
b) Giả sử đường tròn ngoại tiếp tam giác BPQ cắt AB tại K khác B. Chứng minh
rằng AK . AB = AP . AQ.
 Xem đáp án
Xem đáp án
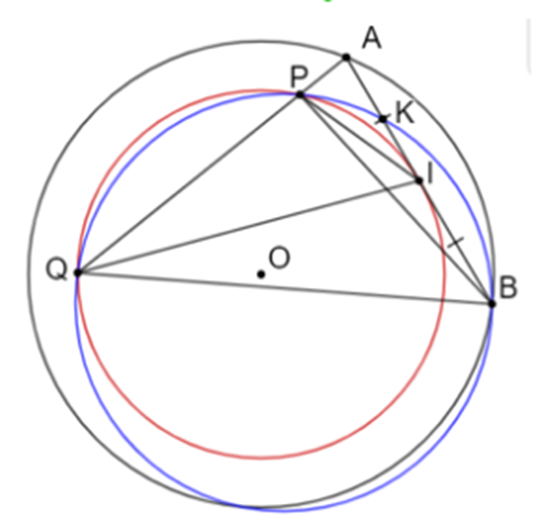
a) Xét (O; OA) có: \[IA = IB = \frac{1}{2}AB\]
⇒ OI ⊥ AB (mối quan hệ đường kính – dây cung)
⇒ OI ⊥ AI
Xét (O; OI) có: OI ⊥ AI
⇒ AI là tiếp tuyến của (O; OI) tại I
\[ \Rightarrow \widehat {PIA} = \widehat {PQI}\] (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn )
Hay \[\widehat {PIA} = \widehat {IQA}\]
Xét ∆AIP và ∆AQI có:
\[\widehat {PIA} = \widehat {IQA}\] (cmt)
\[\widehat A\] chung
Do đó ∆AIP ᔕ ∆AQI (g.g)
Suy ra \[\frac{{AI}}{{AQ}} = \frac{{AP}}{{AI}}\] (hai cạnh tương ứng tỉ lệ)
Do đó AP. AQ = AI2.
b) Vì tứ giác BKPQ nội tiếp nên \[\widehat {APK} = \widehat {KBQ}\]
Hay \[\widehat {APK} = \widehat {ABQ}\]
Xét ∆APK và ∆ABQ có:
\[\widehat {APK} = \widehat {ABQ}\] (cmt)
\[\widehat A\]: góc chung
Do đó ∆APK ᔕ ∆ABQ (g. g)
Suy ra \[\frac{{AP}}{{AB}} = \frac{{AK}}{{AQ}}\] (hai cạnh tương ứng tỉ lệ)
Do đó AK . AB = AP . AQ.
Câu 32:
Một người mua cam với giá 15 000 đồng/1 kg. Người đó bán \[\frac{5}{7}\]số cam với giá 20 000 đồng /1 kg. Còn lại bán với giá 18 000/1 kg. Người đó lãi 620 000 đồng. Hỏi người đó buôn bao nhiêu kg cam?
 Xem đáp án
Xem đáp án
Gọi x (kg) là số cam người đó buôn (x > 0)
Số tiền người đó dùng để mua cam: 15 000x (đồng)
Số tiền thu được khi bán \[\frac{5}{7}\] số cam là: \[20{\rm{ }}000 \cdot \frac{5}{7}x\](đồng)
Số tiền thu được khi bán số cam còn lại là: \[18{\rm{ }}000 \cdot \frac{2}{7}x\] (đồng)
Do người đó lãi 620 000 đồng nên ta có phương trình:
\[20{\rm{ }}000\,\,.\,\,\frac{5}{7}x + 18{\rm{ }}000\,\,.\,\,\frac{2}{7}x - 15{\rm{ }}000\,\,.\,\,x = 620{\rm{ }}000\]
\[ \Leftrightarrow 20\,\,.\,\,\frac{5}{7}x + 18\,\,.\,\,\frac{2}{7}x - 15x = 620\]
\[ \Leftrightarrow \frac{{100}}{7}x + \frac{{{\rm{36}}}}{7}x - 15x = 620\]
\[ \Leftrightarrow \frac{{31}}{7}x = 620\]
⇔ x = 140 (TMĐK)
Vậy người đó buôn 140 kg cam.
Câu 33:
Một người đi từ A đến B gồm các đoạn AC, CD, DB vơi vận tốc theo thứ tự bằng 10 km/giờ, 12 km/giờ, 15 km/giờ. Lúc về, người đó đi BD, DC, CA với vận tốc theo thứ tự bằng 10 km/giờ, 12 km/giờ, 15 km/giờ. Tính quãng đường AB biết thời gian cả đi lẫn về là 3 giờ.
 Xem đáp án
Xem đáp án
Vận tốc trung bình đi và về trên đoạn AC là 12 km/giờ.
Do đó vận tốc trung bình đi và về trên DB cũng bằng 12 km/giờ và vận tốc trung bình cả đi lẫn về trên AB cũng bằng 12 km/giờ.
Quãng đường cả đi lẫn về trên AB là: 12 . 3 = 36 (km)
Quãng đường AB dài là: 36 : 2 = 18 (km)
Vậy quãng đường AB là 18 km.
Câu 34:
Một ô tô đi \[\frac{2}{3}\] quãng đường AB với vận tốc 40 km/giờ, đi tiếp phần còn lại với vận tốc 60 km/giờ. Lúc về ôtô đi với vận tốc không đổi và thời gian về bằng thời gian đi. Tính vận tốc ôtô lúc về?
 Xem đáp án
Xem đáp án
Vì thời gian về bằng thời gian đi nên vận tốc lúc về bằng vận tốc trung bình trên cả quãng đường đi.
Đi 2 km trên đoạn đường đầu hết: \[2 \cdot \frac{1}{{40}} = \frac{1}{{20}}\] (giờ).
Đi 1km trên đoạn đường tiếp theo hết: \[1:60 = \frac{1}{{60}}\] (giờ).
Vậy vận tốc trung bình trên cả quãng đường là:
\[3:\left( {\frac{1}{{20}} + \frac{1}{{60}}} \right) = 45\] (km/giờ).
Vậy vận tốc lúc về là 45 km/giờ.
Câu 35:
Tính \[\frac{5}{{100}}\,\,c{m^2} + \frac{1}{{100}}\,\,d{m^2} = .....\,\,m{m^2}\].
 Xem đáp án
Xem đáp án
Ta có \[\frac{5}{{100}}\,\,c{m^2} = 5\,\,m{m^2}\]
\[\frac{1}{{100}}\,\,d{m^2} = 100\,\,m{m^2}\]
Do đó \[\frac{5}{{100}}\,\,c{m^2} + \frac{1}{{100}}\,\,d{m^2} = 105\,\,m{m^2}\].Câu 36:
Thu gọn: S = 1 + x + x2 + x3 + …. + xn.
 Xem đáp án
Xem đáp án
S = 1 + x + x2 + x3 + …. + xn
⇔ S = x0 + x1 + x2 + x3 + ...... + xn
⇒ xS = x1 + x2 + x3 + ...... + xn+1
⇒ xS – S = x1 + x2 + x3 + ...... + xn+1 – (x0 + x1 + x2 + x3 + ...... + xn)
⇔ S(x – 1) = x1 + x2 + x3 + ...... + xn+1 – x0 – x1 – x2 – x3 – …... – xn
⇔ S(x – 1) = xn+1 – x0
⇔ S(x – 1) = xn+1 – 1
Vậy \[S = \frac{{{x^{n + 1}} - 1}}{{x - 1}}\].
Câu 37:
Giải phương trình: y : 15 – 34,87 = 52,21 + 6
 Xem đáp án
Xem đáp án
y : 15 – 34,87 = 52,21 + 6
⇔ y : 15 – 34,87 = 58,21
⇔ y : 15 = 58,21 + 34,87
⇔ y : 15 = 83,08
⇔ y = 83,08 . 15
⇔ y = 1246,2.
Vậy phương trình đã cho có nghiệm y = 1246,2.
Câu 38:
Tìm hai số, biết hiệu của chúng là 1554 còn tổng của chúng có dạng \[\overline {2x3y} \] chia hết cho 2, cho 5 và cho 9.
 Xem đáp án
Xem đáp án
• \[\overline {2x3y} \] ⁝ 2 và 5 nên y = 0
• \[\overline {2x3y} \] ⁝ 9 ⇒ 2 + x + 3 + y = 5 + x ⁝ 9
Vì x là chữ số nên x = 4 . ta có tổng 2 số là 2430
Số lớn là: (2430 + 1554) : 2 = 1992
Số bé là: 2430 - 1992 = 438
Vậy 2 số cần tìm là 1992 và 438.
Câu 39:
Thu gọn: S = 1 + x + x2 + x3 + …. + xn.
 Xem đáp án
Xem đáp án
S = 1 + x + x2 + x3 + …. + xn
⇔ S = x0 + x1 + x2 + x3 + ...... + xn
⇒ xS = x1 + x2 + x3 + ...... + xn+1
⇒ xS – S = x1 + x2 + x3 + ...... + xn+1 – (x0 + x1 + x2 + x3 + ...... + xn)
⇔ S(x – 1) = x1 + x2 + x3 + ...... + xn+1 – x0 – x1 – x2 – x3 – …... – xn
⇔ S(x – 1) = xn+1 – x0
⇔ S(x – 1) = xn+1 – 1
Câu 40:
Hình chữ nhật ABCD được chia thành 5 hình chữ nhật bằng nhau như hình vẽ tính chu vi hình chữ nhật ABCD biết diện tích hình chữ nhật bằng 432 cm2.
 Xem đáp án
Xem đáp án

Ta chia hình chữ nhật nhỏ thành sáu hình vuông bằng nhau
Diện tích hình vuông là: 4320 : 5 : 6 = 144 (cm2)
Vì 144 = 12 . 12 nên cạnh hình vuông là 12 cm
Chiều dài hình chữ nhật nhỏ: 12 . 3 = 36 (cm)
Chiều rộng hình chữ nhật nhỏ: 12 . 2 = 24 (cm)
Chu vi hình chữ nhật ABCD:
(36 + 36) + (24 + 36) . 2 = 264 (cm).
Vậy chu vi hình chữ nhật ABCD là 264 cm.
Câu 41:
Dưới đây là bảng giá đi xe Taxi của một hãng: 6500 đồng đi \[\frac{1}{2}\] km đầu tiên 5500 đồng thêm mỗi \[\frac{1}{2}\] km (đến km thứ 5), 4 500 đồng thêm mỗi \[\frac{1}{2}\] km nữa. Khoảng cách giữa khách sạn bạn ở đến nơi diễn ra Olympic toán tuổi thơ là 6,5 km. Vậy nếu bạn đi bằng taxi thì phải trả bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Ta có 6,5 = 0,5 + 4,5 + 1,5
Trong 0,5 km đầu hết 6500 đồng
Trong 4,5 (hay \[\frac{9}{2}\]) km tiếp theo hết:
9 . 5500 = 49 500 (đồng)
Trong 1,5 (hay \[\frac{3}{2}\]) km còn lại hết:
3 . 4500 = 13 500 (đồng)
Vậy nếu người đó đi Taxi thì sẽ hết:
6500 + 49 500 + 13 500 = 69 500 (đồng)
Câu 42:
An mua sách hết \[\frac{2}{3}\] số tiền An có, mua vở hết \[\frac{3}{4}\] số tiền còn lại. Sau khi mua sách và vở An còn lại 3 000 đồng. Hỏi lúc đầu An có bao nhiêu tiền?
 Xem đáp án
Xem đáp án
An mua vở hết số phần tiền lúc đầu là:
\[\left( {1 - \frac{2}{3}} \right) \cdot \frac{3}{4} = \frac{1}{4}\] (số tiền lúc đầu)
Số phần tiền An đã dùng là:
\[\frac{2}{3} + \frac{1}{4} = \frac{{11}}{{12}}\] (phần)
Số tiền An có lúc đầu là:
\[3000:\left( {1 - \frac{{11}}{{12}}} \right) = 36{\rm{ }}000\] (đồng)
Đáp số: 36 000 đồng.
Câu 43:
Bạn Mai dùng 25 000 đồng mua bút. Có hai loại bút: Loại I giá 2000 đồng một chiếc, loại II giá 1500 đồng một chiếc. Bạn Mai mua được nhiều nhất bao nhiêu chiếc bút nếu:
a) Mai chỉ mua bút loại I;
b) Mai chi mua bút loại II;
c) Mai mua cả hai loại bút với số lượng như nhau.
 Xem đáp án
Xem đáp án
a) Ta có 25 000 : 2000 = 12 (dư 1000)
Vậy Mai mua được nhiều nhất 12 cây bút loại I.
b) Ta có 25 000 : 1500 = 16 (dư 1000)
Vậy Mai mua được nhiều nhất 16 cây bút loại II.
c) Ta có 25 000 : (2000 + 1500) = 7 (dư 500)
Vậy Mai mua được nhiều nhất 7 cây bút loại I và 7 cây bút loại II.
Câu 44:
 Xem đáp án
Xem đáp án
Gọi số cần tìm là \[\overline {abc} \] (0 < a, c ≤ 9 ; 0 ≤ b ≤ 9)
Có: \[\overline {cab} - \overline {abc} = 765\]
100c + 10a + b – (100a + 10b + c) = 765
99c – 90a – 9b = 765
11c – 10a – b = 85 ⇒ 10c + c – 10a – b = 85
10(c – a) + c – b = 85 (*)
Từ (*) thấy 10(c – a) có chữ số tận cùng là 0
Nên c – b phải có chữ số tận cùng là 5
Vì điều kiện của c và b có: c – b ≤ 9
Do đó c – b = 5
Vì c – b = 5 nên phải có 10(c – a) = 80.
Do đó a = 1, c = 9 là thỏa mãn.
Khi đó a = 1, c = 9, b = 4.
Vậy số cần tìm là 149.
Câu 45:
Cho hình bình hành ABCD, có \[\widehat A = 60^\circ \]. Lấy các điểm E, F theo thứ tự thuộc cạnh AD, CD sao cho DE = CF. Gọi K là điểm đối xứng với F qua BC. Chứng minh EK // AB.
 Xem đáp án
Xem đáp án
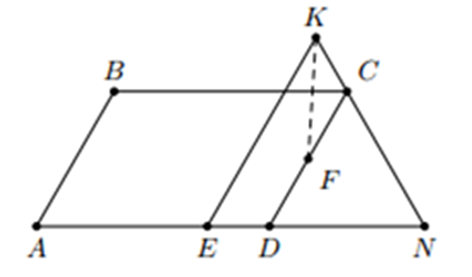
Kéo dài KC cắt AD tại N
Ta có AB // CD nên \[\widehat {BA{\rm{D}}} = \widehat {C{\rm{D}}N} = 60^\circ \]
K đối xứng với F qua BC nên \[\widehat {BC{\rm{D}}} = \widehat {KCB} = 60^\circ \]
\[\widehat {CN{\rm{D}}} = \widehat {KCB} = 60^\circ \]
⇒ Tam giác CND đều ⇒ CN = DN
Lại có CK = DE (cùng = CF)
KN = EN ⇒ tam giác KNE đều
⇒ \[\widehat {KEN} = \widehat {C{\rm{D}}N} = 60^\circ \]
⇒ KE // CD // AB
Câu 46:
Có bao nhiêu số chia hết cho 3 và có 2 chữ số
 Xem đáp án
Xem đáp án
Số nhỏ nhất có hai chữ số chia hết cho 33 là: 12;
Số lớn nhất có hai chữ số chia hết cho 33 là: 99.
Do đó ta có dãy: 12; 15; 18; …...; 96; 99.
Dãy trên có số số hạng là:
(99 − 12) : 3 + 1 = 30(99 − 12) : 3 + 1 = 30 (số hạng)
Vậy có 30 số hạng chia hết cho 3 và có 2 chữ số.
Câu 47:
Hai người đi từ A đến B. Người thứ nhất đi từ A đến B rồi quay lại ngay. Người thứ hai đi từ B đến A rồi quay lại ngay. Hai người này gặp nhau tại C cách A là 6 km. Tính AB biết vận tốc người thứ hai bằng \[\frac{2}{3}\] người thứ nhất.
 Xem đáp án
Xem đáp án
Từ lúc khởi hành đến lúc gặp nhau lần thứ hai ở C, người thứ hai đi được quãng đường là BA + 6 km (1), cả hai người đi được 3AB
Vận tốc của người thứ hai bằng \[\frac{2}{3}\] vận tốc người thứ nhất
Nên quãng đường của người thứ hai đi được bằng \[\frac{2}{5}\] tổng quãng đường hai người đi được tức là bằng: \[3{\rm{A}}B \cdot \frac{2}{5} = \frac{6}{5}AB\] (2)
Từ (1) và (2) suy ra \[\frac{1}{5}AB\] dài 16 km.
Quãng đường AB dài là
\[6:\frac{1}{5} = 30\] (km)
Vậy quãng đường AB là 30 km.
Câu 48:
Khi nhân một số tự nhiên với 235 do sơ ý bạn Cúc đã đặt các tích riêng thứ 2 với thứ 3 thẳng cột nên cúc được kết quả là 10 285. Tìm tích đúng.
 Xem đáp án
Xem đáp án
Khi nhân số A với 235 do sơ ý bạn Cúc đã đặt các tích riêng thẳng cột nên được kết quả là 10 285.
Tức là bạn Cúc đã nhân lần lượt với 5; 20; 30 rồi cộng các kết quả lại .
A . 5 + A . 20 + A . 30 = 10 285
A . 55 = 10 285
A = 10 285 : 55
A = 187
Vậy tích đúng là:
235 . 187 = 43 945
Câu 49:
Một đội công nhân làm 3 ngày, trung bình mỗi ngày sửa đc 1,5 km đường. Ngày thứ nhất và ngày thứ hai sửa đc 3,3 km. Ngày thứ hai và ngày thứ ba sửa đc 2,9 km. Tính mỗi km đường mà mỗi ngày đội đó sửa được.
 Xem đáp án
Xem đáp án
Cả 3 ngày làm được:
1,5 . 3 = 4,5 (km)
Ngày thứ 3 sửa được:
4,5 - 3,3 = 1,2 (km)
Ngày thứ nhất sửa được:
4,5 – 2,9 = 1,6 (km)
Ngày thứ 2 sửa được:
4,5 – 1,2 – 1,6 = 1,7 (km)
Đáp số: Ngày thứ nhất: 1,2 km;
Ngày thứ hai: 1,7 km;
Người thứ ba: 1,6 km.
Câu 50:
Thắng viết lên bảng các số từ 10 đến 70. Mỗi lần, Linh xóa đi 5 số bất kì và viết lại lên bảng trung bình cộng của 5 số đã xóa. Hỏi sau bao nhiêu lần như thế thì Linh chỉ còn lại 1 số trên bảng?
 Xem đáp án
Xem đáp án
Từ 10 đến 70 có số các số là:
(70 − 10) : 1 + 1 = 61(70 − 10) : 1 + 1 = 61 (số)
Khi xóa đi 5 số, viết lại 1 số là số trung bình cộng của số đã xóa thì lúc đó trên bảng sẽ mất đi 4 số so với ban đầu
Sau n lần xóa thì trên bảng đã mất đi số các số là: 4.n (số)
Khi chỉ còn 1 số trên bảng thì trên bảng đã mất đi
61 – 1 = 60 (số)
Khi đó ta có số lần xóa là: 60 = 4 . n hay n = 15
Vậy sau 15 lần xóa.
