- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 81)
-
12938 lượt thi
-
49 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC cân tại A, M thuộc AB, kẻ MN song song BC (N thuộc AC). Chứng minh rằng:
a) Tam giác AMN cân.
b) Kẻ ME song song AC. Chứng minh tam giác MBE cân.
 Xem đáp án
Xem đáp án
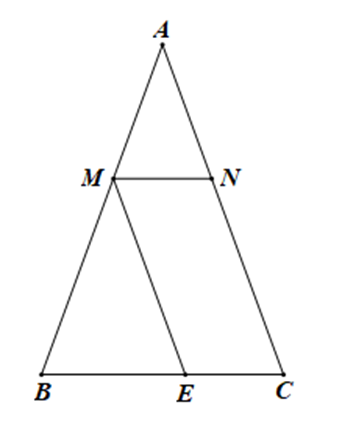
a) Do MN // BC ⇒ \[\widehat {ABC} = \widehat {AMN}\] và \[\widehat {ACB} = \widehat {ANM}\] (2 góc so le trong).
Mà ∆ABC cân tại A \[ \Rightarrow \widehat {ABC} = \widehat {ACB}\]
\[ \Rightarrow \widehat {AMN} = \widehat {ANM}\]
⇒ ∆AMN cân tại A.
b) Do ME // AC ⇒ ME // NC
MN // BC ⇒ MN // EC
⇒ Tứ giác MNCE là hình bình hành.
⇒ \[\widehat {EMN} = \widehat {NCE}\]
Mà \[\widehat {EMN} = \widehat {MEB}\] (2 góc so le trong do MN // BC)
\[\widehat {MBC} = \widehat {NCE}\](do ∆ABC cân tại A)
⇒ \[\widehat {MBE} = \widehat {MEB}\]
⇒ ∆MBE cân tại M.
Câu 2:
Cho đa thức P(x) = x2 + bx + c, trong đó b và c là các số nguyên. Biết đa thức x4 + 6x2 + 25 và đa thức 3x4 + 4x2 + 28x + 5 đều chia hết cho P(x). Tính P(1).
 Xem đáp án
Xem đáp án
Theo bài ra, ta có: (x4 + 6x2 + 25) ⋮ P(x) ⇔ 3(x4 + 6x2 + 25) ⋮ P(x)
Lại có: (3x4 + 4x2 + 28x + 5) ⋮ P(x)
Suy ra: [3(x4 + 6x2 + 25) − (3x4 + 4x2 + 28x + 5)] ⋮ P(x)
⇔ (3x4 + 18x2 + 75 − 3x4 − 4x2 − 28x – 5) ⋮ P(x)
⇔ (14x2 − 28x + 70) ⋮ P(x)
⇔ 14(x2 − 2x + 5) ⋮ P(x)
⇔ (x2 − 2x + 5) ⋮ P(x)
Hay (x4 − 2x + 5) ⋮ (x2 + bx + c)
Mà b, c là các số nguyên nên để (x4 − 2x + 5) ⋮ (x2 + bx + c) thì: b = ‒2, c = 5.
Khi đó, P(1) = 12 − 2.1 + 5 = 1 − 2 + 5 = 4.
Vậy P(1) = 4.
Câu 3:
So sánh 430 và 3.2410.
 Xem đáp án
Xem đáp án
Ta có:
430 = 230.230 = 230.(22)15 = 230.415 = 230.411.44
3.2410 = 3.(3.23)10 = 3.310.230 = 311.230
Mà 411.44 > 311 ⇒ 430 > 3.2410
Câu 4:
Tìm giá trị nhỏ nhất, lớn nhất y = sinx ‒ cosx.
 Xem đáp án
Xem đáp án
Ta có:
y = sinx ‒ cosx
\[ = \sqrt 2 \left( {\frac{1}{{\sqrt 2 }}{\mathop{\rm s}\nolimits} {\rm{inx}} + \frac{1}{{\sqrt 2 }}\cos x} \right)\]
\[ = \sqrt 2 \left( {\cos \frac{\pi }{4}.{\mathop{\rm s}\nolimits} {\rm{inx}} + \sin \frac{\pi }{4}.\cos x} \right)\]
\[ = \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right)\]
\[\sin \left( {x + \frac{\pi }{4}} \right) \in \left[ { - 1;1} \right]\] \[ \Rightarrow \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) \in \left[ { - \sqrt 2 ;\sqrt 2 } \right]\]
Vậy giá trị nhỏ nhất của y là \[ - \sqrt 2 \]; giá trị lớn nhất là \[\sqrt 2 \].
Câu 5:
Tìm tổng tất cả các nghiệm của phương trình sinx = ‒1 trên đoạn bằng [0; 4π].
 Xem đáp án
Xem đáp án
sinx = −1 \[ \Rightarrow x = - \frac{\pi }{2} + k2\pi \]
\[ \Rightarrow 0 \le - \frac{\pi }{2} + k2\pi \le 4\pi \]
\[ \Rightarrow \frac{1}{4} \le k \le \frac{9}{4}\]
⇒ k ∈ {1; 2}.
\[ \Rightarrow x = \left\{ {\frac{{3\pi }}{2};\frac{{7\pi }}{2}} \right\}\].
Tổng tất cả các nghiệm của phương trình đã cho là \[\frac{{3\pi }}{2} + \frac{{7\pi }}{2} = 5\pi \].
Câu 6:
Từ điểm M nằm ngoài đường tròn (O) kẻ các tiếp tuyến MP và MQ với đường tròn biết tam giác MPQ đều cạnh bằng \[15\sqrt 3 \]cm. Tính đường kính của đường tròn.
 Xem đáp án
Xem đáp án
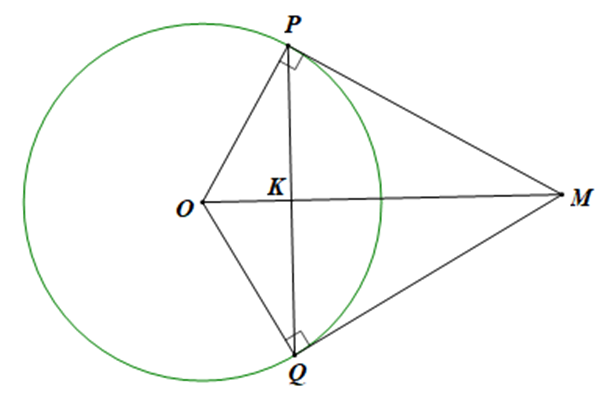
Gọi K là trung điểm của PQ \[ \Rightarrow PK = \frac{1}{2}PQ = \frac{{15\sqrt 3 }}{2}\]
Vì MP là tiếp tuyến của đườn tròn (O) ⇒ OP ⊥ PM \[ \Rightarrow \widehat {OPM} = {90^{\rm{o}}}\]
∆MPQ đều \[ \Rightarrow \widehat {MPQ} = {60^{\rm{o}}}\]\[ \Rightarrow \widehat {OPQ} = \widehat {OPM} - \widehat {MPQ} = {90^{\rm{o}}} - {60^{\rm{o}}} = {30^{\rm{o}}}\]
Xét tam giác OPK có: \[\cos \widehat {OPQ} = \frac{{PK}}{{OP}}\]
\[ \Rightarrow \cos {30^{\rm{o}}} = \frac{{\frac{{15\sqrt 3 }}{2}}}{{OP}}\] \[ \Rightarrow OP = \frac{{15\sqrt 3 }}{2}:\frac{{\sqrt 3 }}{2} = 15\]
Vậy đường kính của đường tròn là: 15.2 = 30 (cm).
Câu 7:
Tìm số tự nhiên n để: n2021 + n2020 + 1 là số nguyên tố.
 Xem đáp án
Xem đáp án
Ta có:
n2021 + n2020 + 1
= n2021 ‒ n2 + n2020 ‒ n + n2 + n +1
= n2(n2019 ‒ 1) + n(n2019 ‒ 1) + (n2 + n +1)
= (n2 + n)(n2019 ‒ 1) + (n2 + n +1)
= n(n + 1)(n2019 ‒ 1) + (n2 + n +1) (1)
Để ý rằng, 2019 chia hết cho 3 và 2019 = 3.673
Nên nếu đặt A = n3 thì n2019 = A673
Mặt khác áp dụng hằng đẳng thức sau:
ak ‒ bk = (a ‒ b)(ak‒1 + ak‒2b1 + ak‒3b2 +...+ a1bk‒2 + bk‒1)
Ta có: n2019 ‒ 1 = A673 ‒ 1 = A673 ‒ 1673 = (A ‒ 1)(A672 + A671 + ... + A1 + 1)
⇒ n2019 ‒ 1 ⋮ (A ‒ 1) hay n2019 ‒ 1 ⋮ (n3 ‒ 1)
Mà n3 ‒ 1 = (n ‒ 1)(n2 + n +1) ⇒ n2019 ‒ 1 ⋮ (n2 + n +1) (2)
Từ (1) và (2) ⇒ n2021 + n2020 + 1 ⋮ (n2 + n +1)
Như vậy để n2021 + n2020 + 1 là một số nguyên tố thì có hai trường hợp:
1. n2 + n +1 = 1, trường hợp này không xảy ra do n > 0 (giả thiết)
2. n2021 + n2020 + 1 = n2 + n +1 hay n2020(n + 1) = n(n + 1) ⇒ n(n + 1)(n2019 ‒ 1) = 0
Do n > 0 nên n2019 ‒ 1 = 0 ⇒ n = 1
Thử lại ta có: n2021 + n2020 + 1 = 12021 + 12020 + 1 = 3 là số nguyên tố.
Vậy n = 1 là đáp án cần tìm.Câu 8:
Tìm số nguyên tố p sao cho p + 8 và p + 16 đều là các số nguyên tố.
 Xem đáp án
Xem đáp án
Xét p = 2 ⇒ p + 8 = 2 + 8 = 10 (loại)
Xét p = 3 ⇒ p + 8 = 3 + 8 = 11 (tm)
p + 16 = 3 + 16 = 19 (tm)
Xét p là số nguyên tố và p > 3 ⇒ p = 3k + 1 hoặc p = 3k + 2
Với p = 3k + 1 ⇒ p + 8 = 3k + 1 + 8 = 3k + 9 = 3(k + 3) (loại)
Với p = 3k + 2 ⇒ p + 16 = 3k + 2 + 16 = 3k + 18 = 3(k + 6) (loại)
Vậy p = 3.
Câu 9:
Tìm tất cả các giá trị thực của tham số m để trên (−1; 1), hàm số \[y = \frac{{mx + 6}}{{2x + m + 1}}\] nghịch biến.
 Xem đáp án
Xem đáp án
ĐKXĐ: \(x \ne \frac{{ - m - 1}}{2}\).
Ta có: \[y = \frac{{mx + 6}}{{2x + m + 1}}\]\( \Rightarrow y' = \frac{{{m^2} + m - 12}}{{{{\left( {2x + m + 1} \right)}^2}}}\).

Câu 10:
Tìm tất các giá trị thực của tham số m để phương trình (m – 2)x + m² – 3m +2 = 0 có tập nghiệm là ℝ.
 Xem đáp án
Xem đáp án
(m – 2)x + m² – 3m +2 = 0
⇔ (m – 2)x = −m2 + 3m ‒ 2
Đề để phương trình (m – 2)x + m² – 3m + 2 = 0 có tập nghiệm là ℝ.
\[ \Leftrightarrow \left\{ \begin{array}{l}m - 2 = 0\\{m^2} - 3m + 2 = 0\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}m = 2\\\left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.\end{array} \right.\]\[ \Leftrightarrow m = 2\]
Vậy m = 2 phương trình (m – 2)x + m² – 3m +2 = 0 có tập nghiệm là ℝ.
Câu 11:
Tìm x để P2 > P biết \[P = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\].
 Xem đáp án
Xem đáp án
Điều kiện xác định: x ≥ 0, x ≠ 1.
Vì P2 > P
⇔ P2 ‒ P > 0
⇔ P(P – 1) > 0
\[ \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}P > 0\\p > 1\end{array} \right.\\\left\{ \begin{array}{l}P < 0\\P < 1\end{array} \right.\end{array} \right.\]
\[ \Rightarrow \left[ \begin{array}{l}P > 1\\P < 0\end{array} \right.\]
+) Với P > 1
\[ \Rightarrow \frac{{\sqrt x + 1}}{{\sqrt x - 1}} > 1\]
\[ \Leftrightarrow \frac{{\sqrt x + 1}}{{\sqrt x - 1}} - 1 > 0\]
\[ \Leftrightarrow \frac{{\sqrt x + 1 - \sqrt x + 1}}{{\sqrt x - 1}} > 0\]
\[ \Leftrightarrow \frac{2}{{\sqrt x - 1}} > 0\], mà 2 > 0
\[ \Rightarrow \sqrt x - 1 > 0\]
\[ \Rightarrow x > 1\]
+) Với P < 0
\[ \Rightarrow \frac{{\sqrt x + 1}}{{\sqrt x - 1}} < 0\]
Mà \[\sqrt x + 1 > 0\]
\[ \Rightarrow \sqrt x - 1 < 0\]
\[ \Leftrightarrow x < 1\]
Mà x ≥ 0, x ≠ 1 ⇒ 0 ≤ x ≤ 1
Vậy để P2 > P khi \[\left[ \begin{array}{l}x > 1\\0 \le x \le 1\end{array} \right.\]
Câu 12:
Từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9, hỏi lập được bao nhiêu số tự nhiên mỗi số có 4 chữ số khác nhau, và trong đó có bao nhiêu số mà chữ số đứng sau lớn hơn chữ số đứng trước.
 Xem đáp án
Xem đáp án
Vì chữ số cần lập có chữ số đứng sau lớn hơn chữ số đằng trước nên không có chữ số 0.
Chọn 4 chữ số khác nhau từ các chữ số 1; 2; 3; 4; 5; 6; 7; 8; 9 có \(C_9^4 = 126\) cách chọn.
Ứng với mỗi cách chọn đó chỉ có duy nhất 1 cách xếp mà chữ số đứng sau lớn hơn chữ số đằng trước.
Vậy có \(C_9^4 = 126\) số tự nhiên thỏa mãn yêu cầu.
Câu 13:
Từ các chữ số của tập hợp {0; 1; 2; 3; 4; 5}, có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau mà trong đó nhất thiết phải có mặt chữ số 0?
 Xem đáp án
Xem đáp án
Số cách đặt chữ số 0 là 4.
Số cách chọn số vào 4 vị trí còn lại là: \[A_5^4 = 120\].
⇒ Số số lập thành là: 4.120 = 480 (số).
Câu 14:
Từ các chữ số 1, 2, 3, 4, 5, 6. Có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau và nhất thiết phải có chữ số 1 và 5
 Xem đáp án
Xem đáp án
Số lập được nhất thiết phải có số 1 và số 5.
⇒ Để chọn 3 số còn lại có: \[C_3^4\] cách chọn
Mỗi số lập được là 1 hoán vị của 5 số.
⇒ Số các số lập được là: \[C_3^4.5 = 480\]số
Câu 15:
 Xem đáp án
Xem đáp án
Ta có:
x5 ‒ x + 2
= x(x4 ‒ 1) +2
= x(x4 ‒ x2 + x2 ‒ 1) + 2
= x(x2 ‒ 1)(x2 + 1) + 2
= x(x2 ‒ x + x ‒ 1)(x2 + 1) + 2
= x(x ‒ 1)(x + 1)(x2 + 1) + 2
Nhận thấy x(x ‒ 1)(x + 1) là tích 3 số nguyên liên tiếp nên chia hết cho 3
⇒ x(x ‒ 1)(x + 1)(x2 + 1) + 2 chia 3 dư 2, không là số chính phương
Vậy x5 ‒ x + 2 không là số chính phương với mọi x thuộc ℤ
Câu 16:
Giải phương trình:
\[\frac{{{x^2}}}{{{x^2} + 2x + 2}} + \frac{{{x^2}}}{{{x^2} - 2x + 2}} = \frac{{5\left( {{x^2} - 5} \right)}}{{{x^4} + 4}} + \frac{{25}}{4}\].
 Xem đáp án
Xem đáp án
\[\frac{{{x^2}}}{{{x^2} + 2x + 2}} + \frac{{{x^2}}}{{{x^2} - 2x + 2}} = \frac{{5\left( {{x^2} - 5} \right)}}{{{x^4} + 4}} + \frac{{25}}{4}\]
\[ \Leftrightarrow \frac{{{x^2}\left( {{x^2} - 2x + 2} \right) + {x^2}\left( {{x^2} + 2x + 2} \right)}}{{{x^4} + 4}} = \frac{{20\left( {{x^2} - 5} \right) + 25\left( {{x^4} + 4} \right)}}{{4\left( {{x^4} + 4} \right)}}\]
⇔ 4(x4 ‒ 2x3 + 2x2 + x4 + 2x3 + 2x2) = 20x2 ‒ 100 + 25x4 + 100
⇔ 4x4 ‒ 8x3 + 8x2 + 4x4 + 8x3 + 8x2 = 25x4 + 20x2
⇔ 8x4 + 16x2 = 25x4 + 20x2
⇔ 17x4 + 4x2 = 0
⇔ x2(17x2 + 4) = 0
Vì 17x2 ≥ 0 với mọi x nên 17x2 + 4 ≥ 4 với mọi x
Vậy x = 0
Câu 17:
Xác định tham số m để hàm số y = f(x) = 3msin4x + cos2x là hàm số chẵn.
 Xem đáp án
Xem đáp án
TXĐ: D = ℝ
⇒ ∀ x ∈ D ⇒ ‒x ∈ D
Ta có:
\[f\left( { - x} \right) = 3m\sin \left( { - 4x} \right) + \cos \left( { - 2x} \right) = - 3m\sin \left( {4x} \right) + \cos \left( {2x} \right)\]
Để hàm số đã cho là hàm số chẵn thì:
f(‒x), = f(x), ∀ x ∈ D
⇔ 3msin4x + cos2x = ‒3m sin4x + cos2x, ∀ x ∈ D
⇔ 6msin4x = 0, ∀ x ∈ D
⇔ m = 0.
Câu 18:
Tìm GTLN, GTNN của: \[y = \sin 2x + \sqrt 3 {\cos ^2}x + 1\] \[\]
 Xem đáp án
Xem đáp án
\[y = \sin 2x + \sqrt 3 {\cos ^2}x + 1\]
\[ = \sin 2x + \sqrt 3 \left( {\frac{{1 + \cos 2x}}{2}} \right) + 1\]
\[ = sin2x + \frac{{\sqrt 3 }}{2}\cos 2x + 1 + \frac{{\sqrt 3 }}{2}\]
\[ = \frac{{\sqrt 7 }}{2}\left( {\sin 2x.\frac{{2\sqrt 7 }}{7} + \frac{{\sqrt {21} }}{7}\cos 2x} \right) + 1 + \frac{{\sqrt 3 }}{2}\]
\[ = \frac{{\sqrt 7 }}{2}.\sin \left( {2x + a} \right) + 1 + \frac{{\sqrt 3 }}{2}\]
Với \[\cos a = \frac{{2\sqrt 7 }}{7}\]; \[\sin a = \frac{{\sqrt {21} }}{7}\]
\[ \Rightarrow - \frac{{\sqrt 7 }}{2} + 1 + \frac{{\sqrt 3 }}{2} \le y \le \frac{{\sqrt 7 }}{2} + 1 + \frac{{\sqrt 3 }}{2}\]
Vậy GTNN của y là \[ - \frac{{\sqrt 7 }}{2} + 1 + \frac{{\sqrt 3 }}{2}\], khi sin(2x + a) = –1
\( \Leftrightarrow 2x + a = - \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)\( \Leftrightarrow x = - \frac{a}{2} - \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\), với \[\cos a = \frac{{2\sqrt 7 }}{7}\]; \[\sin a = \frac{{\sqrt {21} }}{7}\]
Vậy GTLN của y là \[\frac{{\sqrt 7 }}{2} + 1 + \frac{{\sqrt 3 }}{2}\], khi sin(2x + a) = 1
\( \Leftrightarrow 2x + a = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)\( \Leftrightarrow x = - \frac{a}{2} + \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\), với \[\cos a = \frac{{2\sqrt 7 }}{7}\]; \[\sin a = \frac{{\sqrt {21} }}{7}\]
Câu 19:
5 phút bằng một phần mấy của giờ?
 Xem đáp án
Xem đáp án
1 giờ = 60 phút
⇒ 5 phút = \[\frac{5}{{60}}\] giờ \[ = \frac{1}{{12}}\]giờ
Câu 20:
Tìm A hợp B hợp C, biết: \[A = \left[ {1;4} \right]\]; \[B = \left( {2;6} \right)\]; \[C = \left( {1;2} \right)\]
 Xem đáp án
Xem đáp án
\[A \cup B \cup C = \left[ {1;6} \right)\].
Câu 21:
Cho các tập A = {0, 1, 2, 3} , B = {0, 2, 4, 6} , C = {0, 3, 4, 5}.
Tìm (A ∪ B) ∖ (B ∪ C).
 Xem đáp án
Xem đáp án
Ta có: \[A \cup B = \left\{ {0;1;2;3;4;6} \right\}\] và \[B \cup C = \left\{ {0;3;4;5;6} \right\}\].
Do đó (A ∪ B) ∖ (B ∪ C) = {1}.
Câu 22:
Chứng minh biểu thức sau luôn lớn hơn 0 với mọi x:
A = x2 + 5x + 9.
 Xem đáp án
Xem đáp án
Ta có: A = x2 + 5x + 9
\[ = {x^2} + 2.\frac{5}{2}x + \frac{{25}}{4} - \frac{{25}}{4} + 9\]
\[ = {\left( {x + \frac{5}{2}} \right)^2} + \frac{{11}}{4}\]
Vì \[{\left( {x + \frac{5}{2}} \right)^2} \ge 0\] với mọi x
\[ \Rightarrow {\left( {x + \frac{5}{2}} \right)^2} + \frac{{11}}{4} \ge \frac{{11}}{4}\] với mọi x
Vậy A luôn lớn hơn 0 với mọi x.
Câu 23:
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N lần lượt là trung điểm của OB, OD.
a) Chứng minh ANCM là hình bình hành.
b) Qua N kẻ NK song song với OC (K thuộc CD) biết AC = 10cm. Tính NK.
 Xem đáp án
Xem đáp án
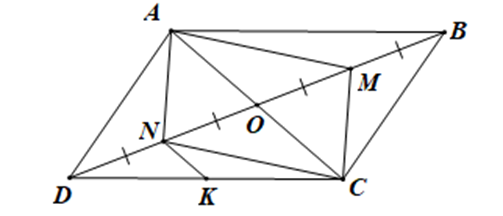
a) Ta có ABCD là hình bình hành
⇒ AC ∩ BD tại trung điểm mỗi đường.
Mà AC ∩ BD ⇒ O là trung điểm của AC, BD.
Lại có M, N lần lượt là trung điểm của OB, OD
\[ \Rightarrow OM = \frac{1}{2}OD = \frac{1}{2}OB = ON\]
⇒ O là trung điểm của MN.
Mà O là trung điểm của AC
⇒ Tứ giác ANCM là hình bình hành.
b) Vì NK // AC, N là trung điểm của DO
\[ \Rightarrow \frac{{NK}}{{OC}} = \frac{{DN}}{{DO}} = \frac{1}{2}\]\[ \Rightarrow NK = \frac{{OC}}{2}\]
Ta có: \[OC = \frac{1}{2}AC = \frac{1}{2}.10 = 5\]
\[ \Rightarrow NK = \frac{5}{2} = 2,5\left( {cm} \right)\].Câu 24:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, cạnh SA vuông góc với (ABCD) và SA = a. Tính khoảng cách SC và BD.
 Xem đáp án
Xem đáp án
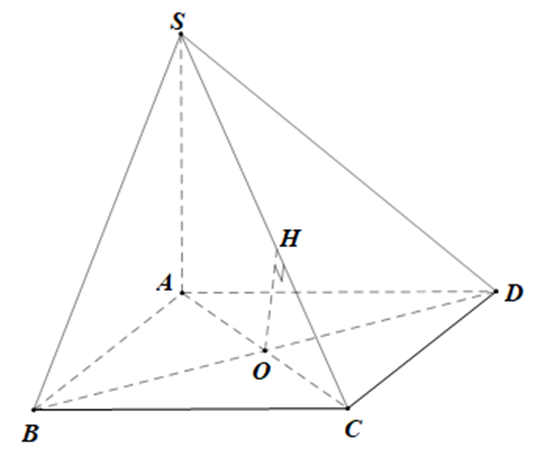
Gọi O là tâm của hình vuông ABCD
Trong mặt phẳng SAC vẽ OH vuông góc với SC (H ∈ SC)
Ta có: BD ⊥ AC, BD ⊥ SA ⇒ BD ⊥ (SAC) ⇒ BD ⊥ OH
Mặt khác OH ⊥ HC.
Vậy OH là đoạn vuông góc chung của SC và BD hay OH là khoảng cách giữa hai đường thẳng chéo nhau SC và BD
\[ \Rightarrow \frac{{SA}}{{SC}} = \frac{{OH}}{{OC}}\]\[ \Rightarrow OH = \frac{{SA.OC}}{{SC}}\]
Ta có:
SA = A, \[OC = \frac{{a\sqrt 2 }}{2}\], \[SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 \]
Vậy \[OH = \frac{{a.\frac{{a\sqrt 2 }}{2}}}{{a\sqrt 3 }} = \frac{{a\sqrt 6 }}{6}\] hay khoảng cách giữa hải đường thẳng SC và BD là \[\frac{{a\sqrt 6 }}{6}\].
Câu 25:
Cho tam giác ABC có E là trung điểm của AC. Qua E kẻ ED // AB (D thuộc BC), EF // BC (F thuộc AB) cho tam giác ABC có E là trung điểm của AC. Chứng minh rằng tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.
 Xem đáp án
Xem đáp án
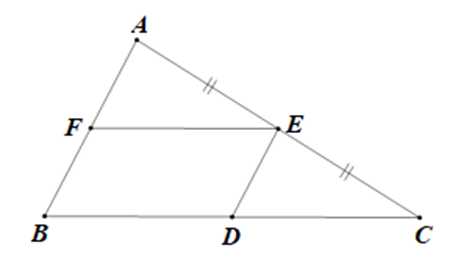
Xét ΔABC có: E là trung điểm của AC và ED // AB
Do đó: D là trung điểm của BC.
Xét ΔABC có: E là trung điểm của AC và EF // BC
Do đó: F là trung điểm của AB.
Xét ΔABC có: F, E lần lượt là trung điểm của AB, AC
Do đó: FE là đường trung bình của ΔBAC.
⇒ FE // BD và FE = BD
Suy ra FEDB là hình bình hành.
Câu 26:
Cho tam giác ABC vuông tại A (AB > AC) có I là trung điểm BC và AH là đường cao. Chứng minh \[BC.IH = \frac{1}{2}\left( {A{B^2} - A{C^2}} \right)\].
 Xem đáp án
Xem đáp án
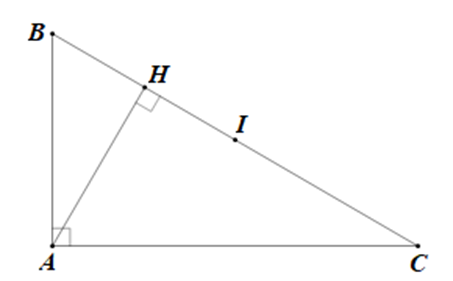
Áp dụng định lí Pythagore ta có: AB2 = AH2 + BH2; AC2 = AH2 + CH2.
Ta có: AB2 ‒ AC2 = AH2 + BH2 ‒ AH2 ‒ CH2
= BH2 ‒ CH2
= (BH ‒ CH)(BH + CH)
= (BI + IH ‒ CH).BC
= (CI ‒ CH + IH).BC (do DABC vuông tại A có I là trung điểm BC nên IA = IB = IC).
= 2IH.BC
\[ \Rightarrow BC.IH = \frac{1}{2}\left( {A{B^2} - A{C^2}} \right)\].
Câu 27:
Cho tam giác nhọn ABC, trực tâm H, M là trung điểm của BC. Qua H kẻ đường thẳng vuông góc với HM, cắt AB và AC theo thứ tự ở E và F.
a) Trên tia đối của tia HC, lấy điểm D sao cho HD = HC. Chứng minh rằng E là trực tâm của tam giác DBH.
b) Chứng minh rằng HE = HF.
 Xem đáp án
Xem đáp án
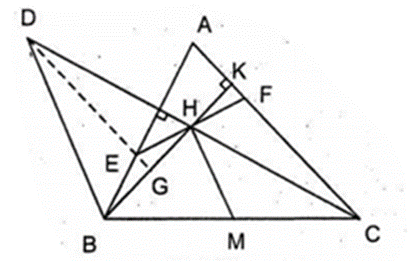
a) Do DH = HC và BM = MC nên HM là đường trung bình tam giác BDC
⇒ HM // BD ⇒ BD ⊥ HE (HM ⊥ HE) ⇒ HE là đường cao ΔBDH (1)
Ta có H là trực tâm nên CH hay CD là đường cao tam giác ABC
⇒ CD ⊥ BA ⇒ DH ⊥ BE ⇒ BE là đường cao ΔBDH (2)
Ta có BE ∩ HE = {E} (3)
Từ (1), (2), (3) ⇒ E là trực tâm ΔBDH.

Câu 28:
Cho tam giác ABC vuông ở A và hình vuông BCDE. Chứng minh rằng:
AB + AC ≤ CE.
 Xem đáp án
Xem đáp án
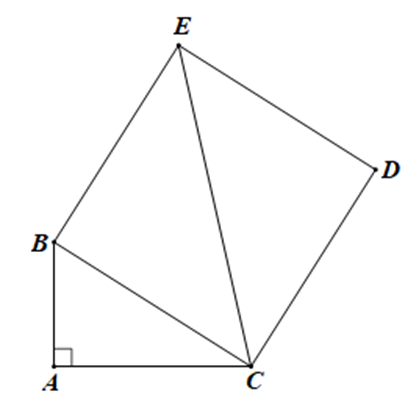
Áp dụng định lí Pythagore cho tam giác vuông ABC ta có: AB2 + AC2 = BC2.
Khi đó (AB + AC)2 = AB2 + AC2 + 2.AB.AC = BC2 + 2.AB.AC
Áp dụng bất đẳng thức Cosi ta có:
2.AB.AC ≤ AB2 + AC2 = BC2
⇒ (AB + AC)2 ≤ BC2 + BC2
Mà BC = BE (do BCDE là hình vuông) và BC2 + BE2 = CE2 (định lí Pythagore cho tam giác vuông BCE)
⇒ (AB + AC)2 ≤ BC2 + BE2 = CE2
⇒ AB + AC ≤ CE
Dấu “=” xảy ra khi AB = AC ⇔ ∆ABC vuông cân ở A.
Câu 29:
Cho tam giác ABC vuông tại A. Vẽ ra ngoài tam giác một hình vuông BCDE. Gọi O là giao điểm hai đường chéo của hình vuông. Chứng minh AO là tia phân giác của \[\widehat {BAC}\].
 Xem đáp án
Xem đáp án
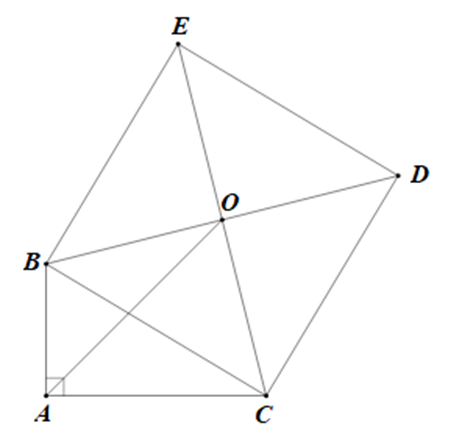
Do BCDE là hình vuông ⇒ BD ⊥ CE
\[\widehat {BAC} = \widehat {BOC} = {90^{\rm{o}}}\]
⇒ 4 điểm B, A, C, O thuộc cùng 1 đường tròn đường kính BC.
\[ \Rightarrow \widehat {BAO} = \widehat {BCO} = {90^{\rm{o}}}\](cùng chắn cung BO)
Mà \[\widehat {BCO} = {45^{\rm{o}}}\] (BCDE là hình vuông)
\[ \Rightarrow \widehat {BAO} = \widehat {BCO} = {45^{\rm{o}}}\], mà \[\widehat {BAC} = {90^ \circ }\], \[\widehat {BAC} = \widehat {BAO} + \widehat {BOC}\]
⇒ \[\widehat {BAO} = \widehat {BOC} = {45^{\rm{o}}}\].
⇒ AO là tia phân giác của \[\widehat {BAC}\].
Câu 30:
Cho tập hợp A = (‒1; 5]; B = (2; 7]. Tìm A \ B.
 Xem đáp án
Xem đáp án
A\B = (‒1; 5] \ (2; 7] = (‒1; 2].
Câu 31:
Chứng minh 52n−1.2n+1 + 3n+1.22n−1 chia hết cho 38.
 Xem đáp án
Xem đáp án
Đặt A = 52n−1.2n+1 + 3n+1.22n−1
Với n = 1, ta có B = 5.4 + 9.2 = 38 chia hết cho 38 hay B ⁝ 38.
Giả sử B ⁝ 38 khi n = k, ta cần chứng minh B ⁝ 38 khi n = k + 1.
Đặt a = 52n−1.2n+1; b = 3n+1.22n−1
Ta có: a + b = 38c, c nguyên
Với n = k + 1 thì B = 50a + 12b = 38a + 12(a + b)
Mà 38a ⁝ 38 và a + b ⁝ 38
Suy ra 12(a + b) ⁝ 38
⇒ B ⁝ 38 (đpcm).
Câu 32:
Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y = \sqrt {5 - m\sin x - (m + 1)\cos x} \] xác định trên ℝ?
 Xem đáp án
Xem đáp án
Hàm số xác định trên ℝ.
\[ \Leftrightarrow 5 - m\sin x - \left( {m + 1} \right)\cos x \ge 0\forall x \in \mathbb{R}\]
⇔ m.sinx ‒ (m+1)cosx ≤ 5 ∀ ∈ ℝ
⇔ m2 + (m+1)2 ≤ 25
⇔ m2 + m ‒ 12 ≤ 0
\[ \Leftrightarrow m \in \left[ { - 4;3} \right]\]
Vậy có 8 giá trị nguyên của m thỏa mãn.
Câu 33:
Cho \[M = \frac{2}{{\sqrt x - 1}} + \frac{2}{{\sqrt x + 1}} - \frac{{5 - \sqrt x }}{{x - 1}}\] với x ≥ 0, x ≠ 1.
a) Rút gọn M.
b) Tính giá trị của M khi x = 4.
c) Tìm x ∈ ℝ để M có giá trị nguyên.
 Xem đáp án
Xem đáp án
a) \[M = \frac{2}{{\sqrt x - 1}} + \frac{2}{{\sqrt x + 1}} - \frac{{5 - \sqrt x }}{{x - 1}}\]
\[ = \frac{{2\left( {\sqrt x + 1} \right) + 2\left( {\sqrt x - 1} \right) - 5 + \sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\]
\[ = \frac{{2\sqrt x + 2 + 2\sqrt x - 2 - 5 + \sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\]
\[ = \frac{{5\sqrt x - 5}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\]
\[ = \frac{{5\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\]
\[ = \frac{5}{{\sqrt x + 1}}\]
b) Với x = 4 thì \[M = \frac{5}{{\sqrt x + 1}} = \frac{5}{{\sqrt 4 + 1}} = \frac{5}{3}\]
c) M có giá trị nguyên \[ \Leftrightarrow \frac{5}{{\sqrt x + 1}}\] có giá trị nguyên.
\[ \Leftrightarrow 5 \vdots \sqrt x + 1\] \[ \Rightarrow \sqrt x + 1 \in \left\{ {1;5} \right\}\]
\[\sqrt x + 1 = 1 \Rightarrow x = 0\]
\[\sqrt x + 1 = 5 \Rightarrow x = 16\]
Câu 34:
Giải phương trình: x3 ‒ 3x ‒ 4 = 0.
 Xem đáp án
Xem đáp án
Đặt \[x = a + \frac{1}{a}\] (a ≠ 0)
Khi đó:
x3 ‒ 3x ‒ 4 = 0
\[ \Leftrightarrow {\left( {a + \frac{1}{a}} \right)^3} - 3\left( {a + \frac{1}{a}} \right) - 4 = 0\]
\[ \Leftrightarrow {a^3} + \frac{1}{{{a^3}}} - 4 = 0\]
⇔ a6 ‒ 4a3 + 1 = 0
⇔ (a3 ‒ 2)2 = 3
\[ \Rightarrow \left[ \begin{array}{l}{a^3} = 2 + \sqrt 3 \\{a^3} = 2 - \sqrt 3 \end{array} \right.\]\[ \Rightarrow \left[ \begin{array}{l}a = \sqrt[3]{{2 + \sqrt 3 }}\\a = \sqrt[3]{{2 - \sqrt 3 }}\end{array} \right.\]
\[ \Rightarrow \left[ \begin{array}{l}x = \sqrt[3]{{2 + \sqrt 3 }} + \frac{1}{{\sqrt[3]{{2 + \sqrt 3 }}}}\\x = \sqrt[3]{{2 - \sqrt 3 }} + \frac{1}{{\sqrt[3]{{2 + \sqrt 3 }}}}\end{array} \right.\]
Câu 35:
Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD ở H và ở K. Chứng minh tứ giác AHCK là hình bình hành.
 Xem đáp án
Xem đáp án
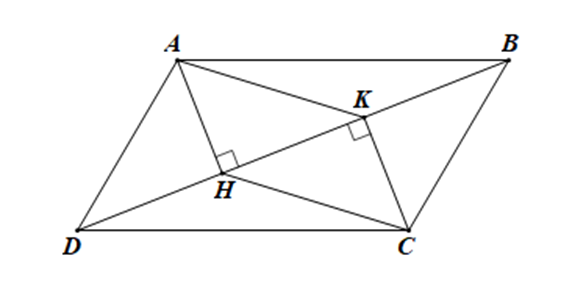
Ta có:
AH ⊥ BD, CK ⊥ BD ⇒ AH // CK (1)
∆ABH và ∆CDK có:
\(\widehat {AHB} = \widehat {CKD}\) (= 90°)
\(\widehat {ABH} = \widehat {CDK}\) (2 góc so le trong)
AB = CD (tính chất hình bình hành)
⇒ ∆ABH = ∆CDK (cạnh huyền – góc nhọn)
⇒ AH = CK (2)
Từ (1), (2) ⇒ tứ giác AHCK là hình bình hành. \[\]
Câu 36:
Cho a + b + c = 0; a2 + b2 + c2 = 2.
Tính giá trị của biểu thức: A = a4 + b4 + c4.
 Xem đáp án
Xem đáp án
Ta có:
a + b + c = 0
⇒ (a + b + c)2 = 0
⇒ a2 + b2 + c2 + 2ab + 2ac + 2bc = 0
⇒ 1 + 2(ab + ac + bc) = 0
\[ \Rightarrow ab + ac + bc = - \frac{1}{2}\]
\[ \Rightarrow {\left( {ab + ac + bc} \right)^2} = \frac{1}{4}\]
\[ \Rightarrow {a^2}{b^2} + {\rm{ }}{a^2}{c^2} + {\rm{ }}{b^2}{c^2} + {\rm{ }}2{a^2}bc{\rm{ }} + {\rm{ }}2a{b^2}c{\rm{ }} + {\rm{ }}2ab{c^2} = \frac{1}{4}\] \[ \Rightarrow {a^2}{b^2} + {\rm{ }}{a^2}{c^2} + {\rm{ }}{b^2}{c^2} + {\rm{ }}2abc\left( {a{\rm{ }} + {\rm{ }}b{\rm{ }} + {\rm{ }}c} \right) = \frac{1}{4}\]
\[ \Rightarrow {a^2}{b^2} + {\rm{ }}{a^2}{c^2} + {\rm{ }}{b^2}{c^2} = \frac{1}{4}\]
Mà a2 + b2 + c2 = 2
⇒ (a2 + b2 + c2)2 = 4
⇒ a4 + b4 + c4 + 2a2b2 + 2a2c2 + 2b2c2 = 4
⇒ a4 + b4 + c4 + 2 (a2b2 + a2c2 + b2c2) = 4
\[ \Rightarrow {a^4} + {\rm{ }}{b^4} + {\rm{ }}{c^4} + {\rm{ }}2.\frac{1}{4} = 4\;\]
\[ \Rightarrow A{\rm{ }} = {\rm{ }}{a^4} + {\rm{ }}{b^4} + {\rm{ }}{c^4} = \frac{7}{2}\]
Câu 37:
Chứng minh nếu n2 chia hết cho 9 thì n chia hết cho 3 (với n là số tự nhiên).
 Xem đáp án
Xem đáp án
Vì n2 chia hết cho 9, ta giả sử n2 = 9k (k ∈ ℕ)
Khi đó 9k là số chính phương.
Mà 9 = 32 nên k là số chính phương, do đó tồn tại số m sao cho k = m2 (m ∈ ℕ)
Từ n2 = 9k ta có \[n = 3\sqrt k = 3m\] nên n chia hết cho 3.
Câu 38:
Cho hai tập hợp X = {n ∈ ℕ⃒n là bội của 4 và 6} và Y = {n ∈ ℕ⃒n là bội của 12}. Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Giải thích:
X = {0; 12; 24; 36; ...}; Y={0; 12; 24; 36;...}
⇒ X = Y
Mệnh đề C là sai. Do đó chọn C.
Câu 39:
Tìm số thích hợp để điền vào dãy số sau: 3; 17; 59; 185; 563; …
 Xem đáp án
Xem đáp án
Đáp án: 1697
Giải thích:
Xét: Hiệu giữa 3 và 17 là 14
Hiệu giữa 17 và 59 là 42 = 14.3
Hiệu giữa 59 và 185 là 126 = 42.3
Hiệu giữa 185và 563 là 378 = 126.3
⇒ Ta có quy luật hiệu của hai số sau sẽ gấp 33 lần hiệu của hai số trước (có lặp lại số ở giữa 22 số kia)
⇒ Số cần điền là: 378.3 + 563 = 1697.
Câu 40:
Một khu đô thị hình chữ nhật được vẽ trên bản đồ 1: 30000. Trên bản đồ chiều dai của khu đô thị là 3cm, chiều rộng là 2cm. Tính diện tích thực tế của khu đô thị.
 Xem đáp án
Xem đáp án
Diện mảnh đất là:
3 × 2 = 6 (cm2)
Diện tích thật của mảnh đất là:
6 × 30000 = 180 000 (cm2).
Đáp số: 180 000 (cm2).
Câu 41:
Thống kê điểm kiểm tra môn Toán của một lớp 10 có 22 học sinh nữ và 20 học sinh nam được cho ở bảng sau:
|
Điểm thi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Tần số |
3 |
2 |
1 |
1 |
3 |
7 |
4 |
8 |
9 |
3 |
1 |
Cho biết đơn vị điều tra và kích thước của mẫu số liệu trên?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đơn vị điều tra: một hsinh lớp 10.
Do lớp học có 22 nữ và 20 nam nên lớp có tất cả 42 học sinh . Do đó; kích thước của mẫu số liệu: 42.
Vậy ta chọn phương án D.
Câu 42:
Cho hình thang ABCD vuông tại A và B, AB = AD = a, BC = 2a. Gọi I là trung điểm của BC. Tính độ dài các vectơ:
a) \[\overrightarrow a = \overrightarrow {BA} - \overrightarrow {BD} - \overrightarrow {DC} \];
b) \[\overrightarrow b = \overrightarrow {DB} - \overrightarrow {DA} + \overrightarrow {IC} \].
 Xem đáp án
Xem đáp án
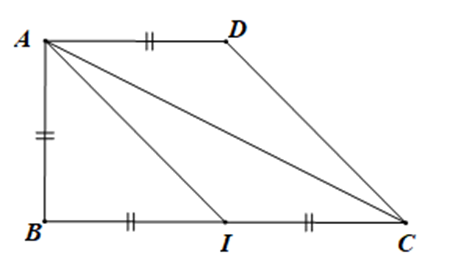
Ta có:
a) \[\left| {\overrightarrow a } \right| = \left| {\overrightarrow {BA} - \overrightarrow {BD} - \overrightarrow {DC} } \right|\]
\[ = \left| {\overrightarrow {DA} - \overrightarrow {DC} } \right|\]\[ = \left| {\overrightarrow {CA} } \right|\]
= CA
\[ = \sqrt {A{B^2} + B{C^2}} \]
\[ = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \]
b) \[\left| {\overrightarrow b } \right| = \left| {\overrightarrow {DB} - \overrightarrow {DA} + \overrightarrow {IC} } \right|\]
\[ = \left| {\overrightarrow {AB} + \overrightarrow {IC} } \right|\]
\[ = \left| {\overrightarrow {AB} + \overrightarrow {BI} } \right|\]\[ = \left| {\overrightarrow {AI} } \right|\]
= AI
\[ = \sqrt {A{B^2} + B{I^2}} \]
\[ = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \].
Câu 43:
Tìm các số nguyên dương x, y, z thỏa mãn:
2xy ‒ 1 = z(x ‒ 1)(y ‒ 1).
 Xem đáp án
Xem đáp án
2xy ‒1 = z(x ‒ 1)(y ‒ 1) = z(xy ‒ x ‒ y + 1)
⇒ 2xy ‒1 = zxy ‒ zx ‒ zy + z
⇒ 2xy = zxy ‒ zx ‒ zy + (z + 1)
⇒ z(x + y) = (z ‒ 2)xy + (z + 1) (*)
Trường hợp 1. z ≤ 2. Mà z ∈ ℕ* nên z = 1 hoặc z = 2
– Nếu z = 1, thay vào (*) ta được:
x + y = ‒xy + 2 ⇒ x + y + xy + 1 = 3 ⇒ (x + 1)(y + 1) = 3
Do x, y ∈ ℕ* nên ta có bảng sau:
|
x + 1 |
1 |
3 |
|
y + 1 |
3 |
1 |
|
x |
0 |
2 |
|
y |
2 |
0 |
⇒ (x; y) ∈ {(0; 2); (2; 0)}.
Þ (x; y; z) ∈ {(0; 2; 1); (2; 0; 1)}.
– Nếu z = 2 ⇒ 2(x + y) = 3 \( \Rightarrow x + y = \frac{3}{2}\) (loại vì x, y ∈ ℕ*).
Trường hợp 2. z > 2 ⇒ (z ‒ 2)xy > 0
Từ z(x + y) = (z ‒ 2)xy + (z + 1) ⇒ z(x + y) > (z ‒ 2)xy
Giả sử x ≥ y ⇒ 2x ≥ x + y ⇒ 2xz ≥ z(x + y) > (z ‒ 2)xy
⇒ 2z > (z − 2)y ⇒ 2z + 2y > zy
– Nếu z ≥ y ⇒ 4z ≥ 2z + 2y > zy ⇒ 4 > y
Mà y ∈ ℕ* nên y ∈ {1, 2, 3}.
• Với y = 1, thay vào (*) ta được z(x + 1) = (z ‒ 2)x + (z + 1)
⇒ zx + z = zx ‒ 2x + z + 1 ⇒ ‒2x + 1 = 0 (vô lý)
• Với y = 2, thay vào (*) ta được z(x + 2) = 2(z ‒ 2)x + (z + 1)
⇒ zx + 2z = 2zx – 4x + z + 1 ⇒ xz – z – 4x + 1 = 0
⇒ z(x ‒ 1) ‒ 4x + 4 = 3 ⇒ z(x ‒ 1) ‒ 4(x – 1) = 3
⇒ (z ‒ 4)(x ‒ 1) = 3
Do x, z ∈ ℕ* nên ta có bảng sau:
|
z – 4 |
1 |
3 |
|
x – 1 |
3 |
1 |
|
z |
5 |
7 |
|
x |
4 |
2 |
⇒ (x; z) ∈ {(4; 5); (2; 7)} thỏa mãn điều kiện.
Þ (x; y; z) ∈ {(4; 2; 5); (2; 2; 7)}.
• Với y = 3, thay vào (*) ta được z(x + 3) = 3(z ‒ 2)x + (z + 1)
Þ zx + 3z = 3zx – 6x + z + 1 Þ 2zx – 2z – 6x + 1 = 0
Þ 2z(x – 1) – 6(x – 1) = 5 Þ (x – 1)(2z – 6) = 5.
Mà 2z – 6 là số chẵn nên ta loại trường hợp này.
– Nếu z ≤ y Þ 4y ≥ 2z + 2y > zy Þ 4 > z.
Kết hợp với z > 2 ta được 2 < z < 4
Mà z ∈ ℕ* nên z = 3
Thay z = 3, thay vào (*) ta được 3(x + y) = (3 ‒ 2)xy + (3 + 1)
Þ 3(x + y) = xy + 4 Þ 3x + 3y – xy = 4
Þ x(3 – y) – 3(3 – y) = –5 Þ (3 – y)(x – 3) = –5
Þ (x – 3)(y – 3) = 5
Do x, y ∈ ℕ* nên ta có bảng sau:
|
x – 3 |
1 |
5 |
|
y – 3 |
5 |
1 |
|
x |
4 |
8 |
|
y |
8 |
4 |
⇒ (x; y) ∈ {(4; 8
Câu 44: Một đội sản xuất chuẩn bị gạo đủ cho 120 công nhân ăn trong 30 ngày. Nhưng phải nhận thêm công nhân nên số gạo dự trữ chỉ đủ ăn trong 15 ngày. Hỏi sau khi nhận thêm công nhân, đội sản xuất có tất cả bao nhiêu người? 1 người ăn hết số gạo đó trong số ngày là: 120 × 30 = 3600 (ngày) Sau khi nhận thêm công nhân, đội sản xuất có tất cả số người là: 3600 : 15 = 240 (người) Đáp số: 240 người.
Câu 45:
Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để bất phương trình x6 + 3x4 − m3x3 + 4x2 − mx + 2 ≥ 0 đúng với mọi x ∈ [1; 3]. Tính tổng của tất cả các phần tử thuộc S.
 Xem đáp án
Xem đáp án
Ta có:
x6 + 3x4 − m3x3 + 4x2 − mx + 2 ≥ 0
⇔ x6 + 3x4 + 4x2 + 2 ≥ (mx)3 + mx
⇔ (x6 + 3x4 + 3x2 + 1) + x2 + 1 ≥ (mx)3 + mx
⇔ (x2 + 1).3 + (x2 + 1) ≥ (mx).3 + mx (∗)
Xét hàm số f(t) = t3 + t ta có: f′(t) = 3t2 + 1 > 0 ∀ t ∈ R ⇒ Hàm số f(t) đồng biến trên ℝ.
Khi đó: (∗) ⇔ x2 + 1 ≥ mx \[ \Leftrightarrow m \le x + \frac{1}{x}\forall x \in \left[ {1;3} \right]\].
Xét hàm số \[g\left( x \right) = x + \frac{1}{x}\], \[x \in \left[ {1;3} \right]\] có: \[{g^'}\left( x \right) = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}} \ge 0\], \[\forall x \in \left[ {1;3} \right]\]
\[ \Rightarrow \mathop {\min g\left( x \right)}\limits_{\left[ {1;3} \right]} = g\left( 1 \right) = 2\]
Để \[ \Leftrightarrow m \le x + \frac{1}{x}\mathop {\forall x \in \left[ {1;3} \right]}\limits_{} \] thì \[\mathop {m \le \min g\left( x \right)}\limits_{\left[ {1;3} \right]} \] ⇔ m ≤ 2
Mà m là số nguyên dương ⇒ m = 1, m = 2 ⇒ S = {1; 2}
Vậy tổng các phần tử của S là 1 + 2 = 3.
Câu 46:
Giải phương trình sau:
(2x + 3) (x + 2)2 (2x + 5) = 315
 Xem đáp án
Xem đáp án
(2x + 3) (x + 2)2 (2x + 5) = 315
⇔ (4x2 +16x + 15)(x2 + 4x + 4)= 315
⇔ (4x2 + 16x + 15)(4x2 + 16x + 16) = 1260
Đặt t = 4x2 + 16x + 15 (t ≥ 0). Phương trình đã cho trở thành:
(t − 1)t = 1260
⇔ (t − 36)(t + 35) = 0
⇔ t = 36
⇔ 4x2 + 16x + 16 = 36
⇔ (x + 2)2 = 3
\[ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 3\\x + 2 = - 3\end{array} \right.\]\[ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 5\end{array} \right.\]
Câu 47:
Cho a + b + c + d = 0. Chứng minh rằng:
a3 + b3 + c3 + d3 = 3.(ab ‒ cd).(c + d).
 Xem đáp án
Xem đáp án
Ta có:
a + b + c + d = 0
⇒ a + b = ‒(c + d)
⇒ (a + b)3 = ‒(c + d) 3
⇒ a3 + b3 + 3ab(a + b) = ‒c3 ‒ d3 ‒ 3cd(c + d)
⇒ a3 + b3 + c3 + d3 = ‒3ab(a + b) ‒ 3cd(c + d)
⇒ a3 + b3 + c3 + d3 = 3ab(c + d) ‒ 3cd(c + d) (vì a + b = ‒ (c + d))
⇒ a3 + b3 + c3 + d3 = 3(c + d)(ab ‒ cd) (đpcm).
Câu 48:
Cho a, b, c, d > 0 và ab + bc + cd + da = 1. Chứng minh rằng:
\[\frac{{{a^3}}}{{b + c + d}} + \frac{{{b^3}}}{{c + d + a}} + \frac{{{c^3}}}{{a + b + c}} \ge \frac{1}{3}\]
 Xem đáp án
Xem đáp án
Theo AM-GM ta có: \(\left\{ {\begin{array}{*{20}{c}}{\frac{{{a^3}}}{{b + c + d}} + \frac{{a\left( {b + c + d} \right)}}{9} \ge \frac{2}{3}{a^2}}\\{\frac{{{b^3}}}{{c + d + a}} + \frac{{b\left( {c + d + a} \right)}}{9} \ge \frac{2}{3}{b^2}}\\{\frac{{{c^3}}}{{d + a + b}} + \frac{{c\left( {d + a + b} \right)}}{9} \ge \frac{2}{3}{c^2}}\end{array}} \right.\)
\( \Rightarrow \frac{{{a^3}}}{{b + c + d}} + \frac{{{b^3}}}{{c + d + a}} + \frac{{{c^3}}}{{d + a + b}} + \frac{{{d^3}}}{{a + b + c}} + \frac{{2\left( {ab + ac + ad + bc + bd + cd} \right)}}{9}\)
\( \ge \frac{2}{3}\left( {{a^2} + {b^2} + {c^2} + {d^2}} \right)\,\,\,\left( 1 \right)\)
Theo AM-GM ta có:
\(3\left( {{a^2} + {b^2} + {c^2} + {d^2}} \right) = \left( {{a^2} + {b^2}} \right) + \left( {{a^2} + {c^2}} \right) + \left( {{a^2} + {d^2}} \right) + \left( {{b^2} + {c^2}} \right) + \left( {{b^2} + {d^2}} \right) + \left( {{c^2} + {d^2}} \right)\)
\( \ge 2\left( {ab + ac + ad + bc + bd + cd} \right)\)
\( \Rightarrow \frac{1}{3}\left( {{a^2} + {b^2} + {c^2} + {d^2}} \right) \ge \frac{2}{9}\left( {ab + ac + ad + bc + bd + cd} \right)\,\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra:
\(\frac{{{a^3}}}{{b + c + d}} + \frac{{{b^3}}}{{c + d + a}} + \frac{{{c^3}}}{{d + a + b}} + \frac{{{d^3}}}{{a + b + c}} \ge \frac{1}{3}\left( {{a^2} + {b^2} + {c^2} + {d^2}} \right)\,\,\,\left( 3 \right)\)
Mặt khác ta có:
\({a^2} + {b^2} + {c^2} + {d^2} = \frac{{{a^2} + {b^2}}}{2} + \frac{{{b^2} + {c^2}}}{2} + \frac{{{c^2} + {d^2}}}{2} + \frac{{{d^2} + {a^2}}}{2} \ge ab + bc + cd + da = 1\,\,\,\left( 4 \right)\)
Từ (3) và (4) suy ra:
\(\frac{{{a^3}}}{{b + c + d}} + \frac{{{b^3}}}{{c + d + a}} + \frac{{{c^3}}}{{d + a + b}} + \frac{{{d^3}}}{{a + b + c}} \ge \frac{1}{3}\).
Dấu "=" xảy ra khi: \(a = b = c = d = \frac{1}{2}\).
Câu 49:
Cho hình chóp S.ABCD có SA vuông góc với đáy, ABCD là hình thoi, góc ABC bằng 60, góc giữa mặt phẳng SBD và ABCD bằng 60°.Khoảng cách từ A đến (SBD) là \[\frac{{a\sqrt 6 }}{4}\]. Tính thể tích khối chóp S.ABCD.
 Xem đáp án
Xem đáp án
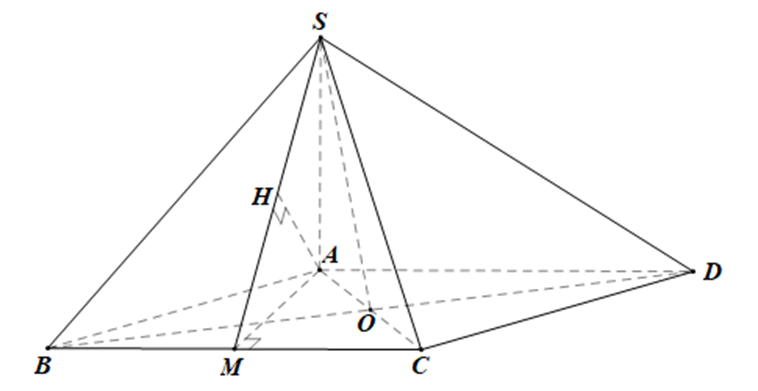
Gọi O là tâm hình thoi ABCD.
⇒ AC ⊥ BD tại O.
ABCD là hình thoi ⇒ AB = AD = BC
Ta có: SA ⊥ (ABCD) ⇒ \[\widehat {SAB} = \widehat {SAD}\], AB = AD, cạnh SA chung
∆SAB = ∆SAD ⇒ SB = SD ⇒ ∆ SBD cân tại S.
⇒ Trung tuyến SO là đường cao
⇒ SO ⊥ BD
Ta có: (SBD) ∩ (ABCD) = BD; SO ⊥ BD; AO ⊥ BD
⇒ Góc giữa (SBD) và (ABCD) là góc giữa SO và AO, là \[\widehat {SOA}\]
\[ \Rightarrow \widehat {SOA} = {60^{\rm{o}}}\].
Giả sử cạnh hình thoi có độ dài là x.
∆ABC có AB = BC và \[\widehat {ABC} = {60^{\rm{o}}}\]⇒ ∆ABC đều ⇒ AC = x \[ \Rightarrow AO = \frac{x}{2}\]
Xét ∆SAO vuông tại A: \[\tan \widehat {SAO} = \frac{{SA}}{{AO}}\] \[ \Rightarrow SA = AO.\tan \widehat {SAO}\]
\[ \Rightarrow SA = \frac{x}{2}.\tan {60^{\rm{o}}} = \frac{{x\sqrt 3 }}{2}\]
∆SAB = ΔSAC ⇒ SB = SC ⇒ ΔSBC cân tại S
Gọi M là trung điểm của BC ⇒ SM ⊥ BC
∆ABC đều ⇒ AM ⊥ BC và \(AM = \frac{{x\sqrt 3 }}{2}\) ⇒ BC ⊥ (SAM)
Kẻ AH ⊥ SM.
⇒ BC ⊥ AH ⇒ AH ⊥ (SBC)
⇒ Khoảng cách từ A đến (SBC) là AH \[ \Rightarrow AH = \frac{{a\sqrt 6 }}{4}\]
Xét ∆AHM vuông tại H có:\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{M^2}}}\] (hệ thức lượng trong tam giác vuông)
\[ \Rightarrow \frac{1}{{{{\left( {\frac{{a\sqrt 6 }}{2}} \right)}^2}}} = \frac{1}{{{{\left( {\frac{{x\sqrt 3 }}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{x\sqrt 3 }}{2}} \right)}^2}}}\]
\[ \Rightarrow \frac{{16}}{{{a^2}.6}} = 2.\frac{4}{{{x^2}.3}}\] \[ \Rightarrow x = a\]
Khi đó \[SA = \frac{{a\sqrt 3 }}{2}\]; \(AM = \frac{{a\sqrt 3 }}{2}\); \(BC = x = a\).
\[ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}.SA.{S_{ABCD}} = \frac{1}{3}.SA.AM.BC = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 3 }}{2}.a = \frac{{{a^3}}}{4}\] (đơn vị thể tích).
