- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 82)
-
12934 lượt thi
-
44 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
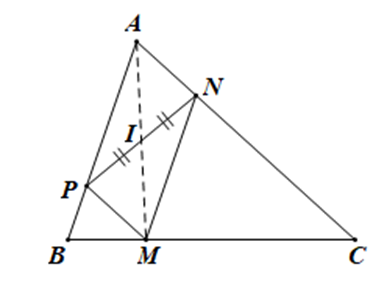
Ta có:
NM // AB ⇒ MN // AP
MP // AC ⇒ MP // AN
⇒ Tứ giác APMN là hình bình hành có 2 đường chéo AM và PN.
Mà I là trung điểm của NP
⇒ I cũng là trung điểm của AM hay A, I, M thẳng hàng.
Câu 2:
Thu gọn biểu thức: \(\frac{{x{}^6 - {y^6}}}{{{x^4} - {y^4} - {x^3}y + x{y^3}}}\).
 Xem đáp án
Xem đáp án
Ta có: \(\frac{{{x^6} - {y^6}}}{{{x^4} - {y^4} - {x^3}y + x{y^3}}}\)
\( = \frac{{{{\left( {{x^2}} \right)}^3} - {{\left( {{y^2}} \right)}^3}}}{{\left( {{x^4} - {y^4}} \right) - \left( {{x^3}y - x{y^3}} \right)}}\)\( = \frac{{\left( {{x^3} - {y^3}} \right)\left( {{x^3} + {y^3}} \right)}}{{{x^3}\left( {x - y} \right) + {y^3}\left( {x - y} \right)}}\)
\( = \frac{{\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)\left( {{x^3} + {y^3}} \right)}}{{\left( {x - y} \right)\left( {{x^3} + {y^3}} \right)}}\)\( = {x^2} + xy + {y^2}\).
Câu 3:
Tìm một số có hai chữ số, biết rằng nếu viết chữ số 0 xen giữa hai chữ số của số đó thì được một số có ba chữ số, gấp 9 lần số ban đầu. Tìm số đã cho.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là \[\overline {ab} \] (a,b là chữ số; a khác 0)
Theo đề bài \[\overline {ab} .9{\rm{ }} = \;\overline {a0b} \]
⇒ 90a + 9b = 100a + b
⇒ 100a ‒ 90a = 9b ‒ b
⇒ 10a = 8b
Vì a ≠ 0 và a,b là chữ số nên a = 4 ⇒ b = 5.
Số cần tìm là 45.
Câu 4:
Tìm m để đa thức x3 + y3 + z3 + mxyz chia hết cho đa thức x+ y + z.
 Xem đáp án
Xem đáp án
Ta có:
x3 + y3 + z3 + mxyz
= (x + y + z)3 − 3(x + y)(y + z)(x + z) + mxyz
= (x + y + z)3 − 3[xy(x + y) + yz( y+ z) + xz(x + z) + 2xyz] + mxyz
= (x + y + z)3 − 3[xy(x + y + z) + yz(x + y + z) + xz(x + y + z) − xyz] + mxyz
= (x + y + z)3 − 3(x + y + z)(xy + yz + xz) + 3xyz + mxyz
= (x + y + z)(x2 + y2 + z2 − xy − yz − xz) + (m + 3).xyz
Như vậy, để x3 + y3 + z3 + mxyz chia hết cho đa thức x+ y + z ∀x, y, z thì (m + 3)xyz ⋮ (x + y + z), ∀x, y, z
⇒ m + 3 = 0 ⇒ m = −3.
Câu 5:
Cho (O; R) và (O'; R') tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O') sao cho AM vuông góc với AN.
a) Chứng minh: OM // ON.
b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO’ lớn nhất.
 Xem đáp án
Xem đáp án
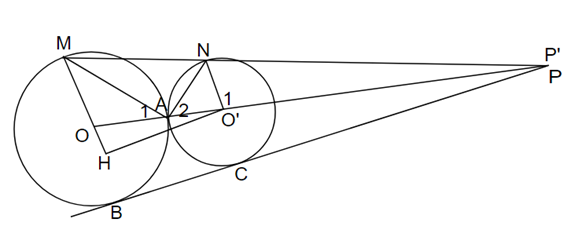
a) Ta có: \({\widehat O_1} = {180^{\rm{o}}} - 2{\widehat A_1}\)
\(\widehat {{{O'}_1}} = 2{\widehat A_2} = 2\left( {{{90}^{\rm{o}}} - {{\widehat A}_1}} \right) = {180^{\rm{o}}} - 2{\widehat A_1}\)
Do đó: \({\widehat O_1} = \widehat {{{O'}_1}} \Rightarrow OM\,{\rm{//}}\,O'N\)
b) Gọi \(P\) là giao điểm của \(MN\) và \(OO'\)
Ta có: \(\frac{{PO'}}{{PO}} = \frac{{O'N}}{{OM}} = \frac{{R'}}{R}\)
Gọi \(P'\) là giao điểm của \(BC\) và \(OO'\)
Vì \(OB\,{\rm{//}}\,O'C\) nên \(\frac{{P'O'}}{{P'O}} = \frac{{O'C}}{{OB}} = \frac{{R'}}{R}\).
Suy ra \(P'\) trùng với \(P\) (vì cùng ở ngoài đoạn thẳng \(OO'\) theo tỉ số \(\frac{{R'}}{R}\)).
Câu 6:
Lớp 10A có 45 học sinh, trong đó 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào trong 3 môn trên và 5 em thích cả 3 môn. Hỏi có bao nhiêu em thích 1 môn trong 3 môn trên?
 Xem đáp án
Xem đáp án
Gọi a, b, c theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;
x là số học sịnh chỉ thích hai môn là Văn và Toán;
y là số học sịnh chỉ thích hai môn là Sử và Toán;
z là số học sịnh chỉ thích hai môn là Văn và Sử.
Ta có số em thích ít nhất một môn là 45 − 6 = 39
Ta có hệ phương trình:
\[\left\{ \begin{array}{l}a + x + z + 5 = 25\,\,\,\,\,\,\left( 1 \right)\\b + y + z + 5 = 18\,\,\,\,\,\,\,\left( 2 \right)\\c + x + y + 5 = 20\,\,\,\,\,\,\,\left( 3 \right)\\x + y + z + a + b + c + 5 = 39\,\,\,\,\left( 4 \right)\end{array} \right.\]
Cộng vế với vế (1), (2), (3) ta có:
a + b + c + 2(x + y + z) + 15 = 63 (5)
Từ (4) và (5) ta có:
a + b + c + 2(39 − 5 − a − b − c) + 15 = 63
⇔ a + b + c = 20.
Vậy chỉ có 2020 em thích chỉ một môn trong ba môn trên.
Câu 7:
Tìm x, biết: 3x(x ‒ 1) + x ‒ 1 = 0.
 Xem đáp án
Xem đáp án
3x(x ‒ 1) + x ‒ 1 = 0
⇒ 3x(x ‒ 1) + (x ‒ 1) = 0
⇒ (3x + 1)(x ‒ 1) = 0
\[ \Rightarrow \left[ \begin{array}{l}3x + 1 = 0\\x - 1 = 0\end{array} \right.\]\[ \Rightarrow \left[ \begin{array}{l}x = \frac{{ - 1}}{3}\\x = 1\end{array} \right.\]
Câu 8:
Nêu mệnh đề phủ định và xét tính đúng sai của mệnh đề sau:
A: “Với mọi n ∈ ℕ*, (1 + 2 + .... + n) không chia hết cho 11”.
 Xem đáp án
Xem đáp án
Mệnh đề sai.
Mệnh đề phủ định là: Với mọi n ∈ ℕ*, (1 + 2 + .... + n) chia hết cho 11.
\[P = 1 + 2 + ... + n = \frac{{n\left( {n + 1} \right)}}{2}\], n = 11
⇒ P chia hết cho 11.
Vậy tồn tại số tự nhiên n để P chia hết cho 11.
Câu 10:
Nếu 2x + 2y = 2x + y. Tính \[\frac{{dy}}{{dx}}\].
 Xem đáp án
Xem đáp án
\(\ln {2.2^x} + \ln {2.2^y}\frac{{dy}}{{dx}} = \ln {2.2^{x + y}}\left( {1 + \frac{{dy}}{{dx}}} \right)\)
\( \Rightarrow {2^x} + {2^y}\frac{{dy}}{{dx}} = {2^{x + y}}\left( {1 + \frac{{dy}}{{dx}}} \right)\)
\( \Rightarrow {2^x} + {2^y}\frac{{dy}}{{dx}} = {2^{x + y}} + {2^{x + y}}\frac{{dy}}{{dx}}\)
\( \Rightarrow \left( {{2^y} - {2^{x + y}}} \right)\frac{{dy}}{{dx}} = \left( {{2^{x + y}} - {2^x}} \right)\)
\( \Rightarrow \frac{{dy}}{{dx}} = \frac{{{2^{x + y}} - {2^x}}}{{{2^y} - {2^{x + y}}}}\)
\( \Rightarrow \frac{{dy}}{{dx}} = \frac{{{2^x}\left( {{2^y} - 1} \right)}}{{{2^y}\left( {1 - {2^x}} \right)}}\)
\( \Rightarrow \frac{{dy}}{{dx}} = {2^{x - y}}\left( {\frac{{{2^y} - 1}}{{1 - {2^x}}}} \right)\).
Câu 11:
Giải phương trình: \[3\sin \left( {4x + \frac{\pi }{3}} \right) - 4 = 0\].
 Xem đáp án
Xem đáp án
\[3\sin \left( {4x + \frac{\pi }{3}} \right) - 4 = 0\]
\[ \Leftrightarrow \sin \left( {4x + \frac{\pi }{3}} \right) = \frac{4}{3}\]
Do \[\sin \left( {4x + \frac{\pi }{3}} \right) \le 1\] mà \[\frac{4}{3} > 1\] nên phương trình vô nghiệm.
Câu 13:
Tìm tất cả giá trị nguyên của m để phương trình:
\[8{\sin ^2}x + \left( {m - 1} \right)\sin 2x + 2m - 6 = 0\] có nghiệm.
 Xem đáp án
Xem đáp án
\[8{\sin ^2}x + \left( {m - 1} \right)\sin 2x + 2m - 6 = 0\]
\[ \Leftrightarrow 8.\frac{{1 - \cos 2x}}{2} + \left( {m - 1} \right)\sin 2x + 2m - 6 = 0\]
\[ \Leftrightarrow 4 - 4\cos 2x + \left( {m - 1} \right)\sin 2x + 2m - 6 = 0\]
\[ \Leftrightarrow 4\cos 2x - \left( {m - 1} \right)\sin 2x = 2m - 2\]
Phương trình có nghiệm:
\[ \Leftrightarrow {4^2} + {\left( {m - 1} \right)^2} \ge {\left( {2m - 2} \right)^2}\]
\[ \Leftrightarrow 16 + {m^2} - 2m + 1 \ge 4 - 8m + 4{m^2}\]
\[ \Leftrightarrow 3{m^2} - 6m - 13 \le 0\]
\[ \Leftrightarrow \frac{{3 - 4\sqrt 3 }}{3} \le m \le \frac{{3 + 4\sqrt 3 }}{3}\]
Vì m ∈ ℤ ⇒ m ∈ {‒1; 0; 1; 2; 3}.
Câu 14:
Rút gọn phân thức: \[\frac{{{a^2} + {b^2} - {c^2} + 2ab}}{{{a^2} - {b^2} + {c^2} + 2ac}}\].
 Xem đáp án
Xem đáp án
\[\frac{{{a^2} + {b^2} - {c^2} + 2ab}}{{{a^2} - {b^2} + {c^2} + 2ac}}\]
\[ = \frac{{{{\left( {a + b} \right)}^2} - {c^2}}}{{{{\left( {a + c} \right)}^2} - {b^2}}}\]
\[ = \frac{{\left( {a + b - c} \right)\left( {a + b + c} \right)}}{{\left( {a + c - b} \right)\left( {a + c + b} \right)}}\]
\[ = \frac{{a + b - c}}{{a + c - b}}\].
Câu 15:
Cho (O; R) và (O; R’) tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O’) sao cho AM vuông góc với AN chứng minh:
a) OM // O’N.
b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO’ lớn nhất.
 Xem đáp án
Xem đáp án
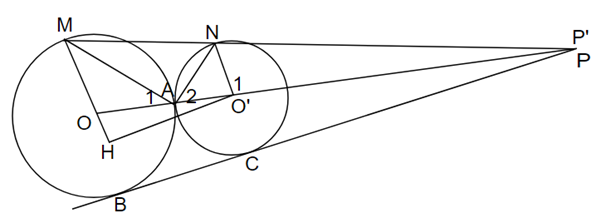
a) Ta có : \(\widehat {MOA} = {\widehat O_1}\left( { = {{180}^{\rm{o}}} - 2{{\widehat A}_1}} \right)\)
Þ O’N // OM.
Gọi P là giao điểm của MN và OO’.
Ta có : \(\frac{{O'P}}{{OP}} = \frac{{O'N}}{{OM}} = \frac{{R'}}{R}\)
Gọi P’ là giao điểm của BC và OO’, ta có:
\(\frac{{O'P'}}{{OP'}} = \frac{{O'C}}{{OB}} = \frac{{R'}}{R}\)
Suy ra P’ ≡ P.
b) Gọi H là hình chiếu của O' trên OM
Tứ giác MNO'O là hình thang nên \(S = \frac{{\left( {OM + O'N} \right)O'H}}{2}\)
\(S = \frac{{R + R'}}{2} \cdot O'H \le \frac{{R + R'}}{2}.OO' = \frac{{{{\left( {R + R'} \right)}^2}}}{2}\)
Dấu "=" xảy ra khi \(H \equiv O \Leftrightarrow OM \bot OO'\)
Vậy để diện tích tứ giác OMNO’ lớn nhất thì OM ⊥ OO’.
Câu 16:
Cho nửa đường tròn (O; R) đường kính BC và một điểm A trên nửa đường tròn (A khác B, C). Hạ AH vuông góc BC tại H. Trên nửa mp bờ BC chứa A dựng 2 nửa đường tròn đường kính HB, HC chúng lần lượt cắt AB, AC tại E và F. Chứng minh AE.AB = AF.AC.\[\]
 Xem đáp án
Xem đáp án
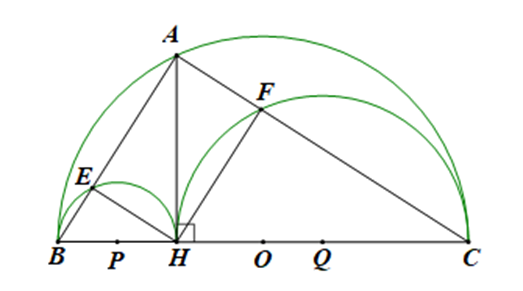
Gọi P, Q lần lượt là tâm của hai nửa đường tròn đường kính HB và HC.
Ta có:
\[\widehat {BEH} = {90^{\rm{o}}}\](góc nội tiếp chắn nửa đường tròn đường kính HB).
\[\widehat {HFC} = {90^{\rm{o}}}\] (góc nội tiếp chắn nửa đường tròn đường kính HC).
Tam giác ABH vuông tại H có HE là đường cao:
AH2 = AE.AB (hệ thức lượng trong tam giác vuông) (1)
Tam giác ACH vuông tại H có HF là đường cao:
AH2 = AF.AC (hệ thức lượng trong tam giác vuông) (2)
Từ (1), (2) ⇒ AE.AB = AF.AC
Câu 17:
Cho hai tập hợp A = {x ∈ ℝ | 1≤ |x| ≤ 2}; B = (–∞; m – 2] ∪ [m; +∞).
Tìm tất cả các giá trị của m để A ⊂ B.
 Xem đáp án
Xem đáp án
Ta có: \[A = \left[ { - 2; - 1} \right] \cup \left[ {1;2} \right]\]; \[B = \left( { - \infty ;m - 2} \right] \cup \left[ {m; + \infty } \right)\]
Để A ⊂ B, ta có:
TH1: \[\left\{ \begin{array}{l}m - 2 \ge - 1\\m \le 1\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}m \ge 1\\m \le 1\end{array} \right.\]\[ \Leftrightarrow m = 1\].
TH2. m ≤ 2.
TH3. m ‒ 2 ≥ 2 ⇔ m ≥ 4.
Vậy \[\left[ \begin{array}{l}m \ge 4\\m \le - 2\\m = 1\end{array} \right.\] thì A ⊂ B.
Câu 18:
Cho hàm số (c) có y = f(x) = x2 ‒ 2x + 3. Viết phương trình tiếp tuyến với (c) tại điểm thuộc (c) có hoành độ x0 = 1.
 Xem đáp án
Xem đáp án
f′(x) = 2x − 2
Do phương trình tiếp tuyến với (c) tại điểm thuộc (c) có hoành độ x0 = 1 nên thay x = 1 vào f’(c) ta có: f(1) = 2
Phương trình tiếp tuyến: y = 2.
Câu 19:
Cho hàm số \[y = f\left( x \right) = \frac{{3x + 1}}{{1 - x}}\] (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành.
 Xem đáp án
Xem đáp án
Gọi M là giao điểm của (C) với trục hoành \[ \Rightarrow M\left( { - \frac{1}{3};0} \right)\].
\[y' = \frac{{3\left( {1 - x} \right) + 3x + 1}}{{{{\left( {1 - x} \right)}^2}}} = \frac{4}{{{{\left( {1 - x} \right)}^2}}}\]
\[y'\left( { - \frac{1}{3}} \right) = \frac{9}{4}\].
Phương trình tiếp tuyến: \[y = \frac{9}{4}\left( {x + \frac{1}{3}} \right) + 0 = \frac{9}{4}x + \frac{3}{4}\].
Câu 20:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a, CD = a . Góc giữa 2 mặt phẳng (SBC) và (ABCD) bằng 60° .Gọi I là trung điểm của cạnh AD. Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt đáy. Tính thể tích khối chóp SABCD theo a.
 Xem đáp án
Xem đáp án
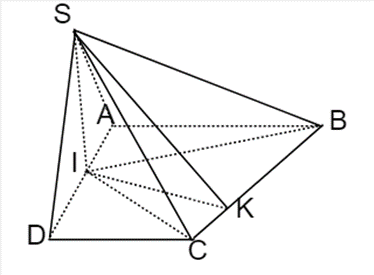
Do (SBI) ⊥ (ABCD), (SCI) ⊥ (ABCD) ⇒ SI ⊥ (ABCD)
Kẻ IK ⊥ BC (K thuộc BC) ⇒ BC ⊥ (SIK) ⇒ \[\widehat {SKI} = {60^{\rm{o}}}\]
Diện tích hình thang ABCD bằng: 3a2
Tổng diện tích ∆ABI và ∆CDI bằng \[\frac{{3{a^2}}}{2}\]⇒ S∆IBC = \[\frac{{3{a^2}}}{2}\]
\[BC = \sqrt {{{\left( {AB - CD} \right)}^2} + A{D^2}} = a\sqrt 5 \]
\[ \Rightarrow IK = \frac{{2{S_{\Delta IBC}}}}{{BC}} = \frac{{3\sqrt 5 a}}{5}\]
\[ \Rightarrow SI = IK.\tan \widehat {SKI} = \frac{{3\sqrt {15} a}}{5}\]
Thể tích khối chóp S.ABCD là: \[V = \frac{1}{3}{S_{ABCD}}.SI = \frac{{3\sqrt {15} {a^2}}}{5}\].
Câu 21:
Cho A = (2 – m; 4) và B = [m; +∞). Tìm m để A ∩ B = ∅.
 Xem đáp án
Xem đáp án
Với A = (2 – m; 4) và B = [m; +∞), để A ∩ B= ∅ thì 2 ‒ m < 4 ≤ m
\( \Leftrightarrow \left\{ \begin{array}{l}m > - 2\\m \ge 4\end{array} \right. \Leftrightarrow m \ge 4\).
Câu 22:
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB, AC theo thứ tự D, E. Chứng minh rằng DE = BD + CE.
 Xem đáp án
Xem đáp án
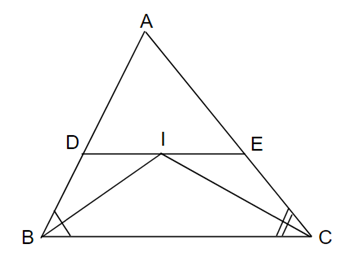
Ta có: BI là tia phân giác \[\widehat B\]\[ \Rightarrow \widehat {DBI} = \widehat {IBC}\]
Mà \[\widehat {DIB} = \widehat {IBC}\] (2 góc so le trong do DE // BC)
\[ \Rightarrow \widehat {DIB} = \widehat {DBI}\]⇒ ∆ DBI cân tại D.
⇒ BD = DI.
Ta có: CI là phân giác \[\widehat C\] \[ \Rightarrow \widehat {ECI} = \widehat {ICB}\]
Mà \[\widehat {EIC} = \widehat {ICB}\] (2 góc so le trong do DE // BC)
\[ \Rightarrow \widehat {ECI} = \widehat {EIC}\] ⇒ ∆CEI cân tại E.
⇒ CE = IE.
Ta có: BD = DI; CE = IE
⇒ BD + CE = DI + IE
Hay BD + CE = DE.
Câu 23:
Cho tam giác ABC vuông cân tại A, \[AB = \sqrt 2 \]. Về phía ngoài tam giác vẽ tam giác ACD vuông cân tại D .
a) Tứ giác ABCD là hình gì? Vì sao?
b) Tính diện tích ABCD.
 Xem đáp án
Xem đáp án
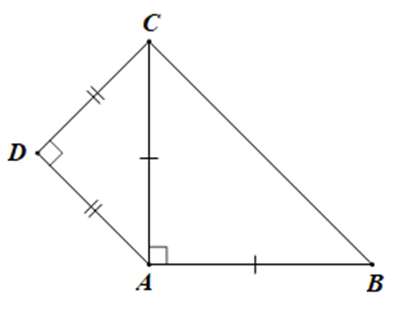
∆ABC vuông cân \[ \Rightarrow \widehat {ABC} = \widehat {ACB}\].
∆ADC vuông cân tại D \[ \Rightarrow \widehat {ACD} = \widehat {DAC}\].
Ta có: \[\widehat {BCD} = \widehat {ACB} + \widehat {ACD} = {45^{\rm{o}}} + {45^{\rm{o}}} = {90^{\rm{o}}}\]
⇒ BC ⊥ CD
Ta lại có AD ⊥ CD ⇒ AD // BC
Xét tứ giác ADCB có:
AD // BC, \[\widehat {ADC} = \widehat {DCB} = {90^{\rm{o}}}\].
⇒ ADCB là hình thang vuông
Khi đó \[BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {2 + 2} = 2\]
Xét ∆ADC vuông cân tại D có: \[\sin \widehat {DCA} = \frac{{AD}}{{AC}}\]
\[ \Rightarrow AD = \sin \widehat {DCA}.AC = \sin {45^{\rm{o}}}.\sqrt 2 = \frac{{\sqrt 2 }}{2}.\sqrt 2 = 1\].
⇒ AD = DC = 1.
Vậy diện tích hình thang vuông ADCB là:
\[S = \frac{{AD + BC}}{2}.CD = \frac{{1 + 2}}{2}.1 = \frac{3}{2}\].
Câu 24:
Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ (M ∈ OP), IN // OP (N ∈ OQ). Chứng minh rằng:
a) Tam giác IMN cân tại I.
b) OI là đường trung trực của MN.
 Xem đáp án
Xem đáp án
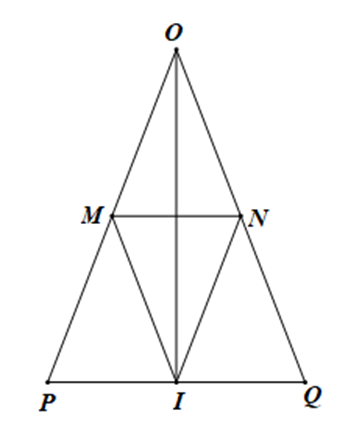
a) Xét ΔOPQ có: I là trung điểm của PQ, IN // OP
⇒ N là trung điểm của OQ.
Xét ΔOPQ có: I là trung điểm của PQ, IM // OQ
⇒ M là trung điểm của OP.
Xét ΔMPI và ΔNQI có:
MP = NQ; \[\widehat {MPI} = \widehat {NQI}\]; PI = QI
Do đó: ΔMPI = ΔNQI (c.g.c)
⇒ IM = IN (hai cạnh tương ứng)
⇒ ΔIMN cân tại I.
b) Ta có: OM = ON
Nên O nằm trên đường trung trực của MN (1)
Ta có: IM = IN
Nên I nằm trên đường trung trực của MN (2)
Từ (1) và (2) suy ra OI là đường trung trực của MN.
Câu 25:
Cho tập hợp A = (0; +∞) và B = {x ∈ ℝ | mx2 ‒ 4x + m ‒ 3 = 0}. Tìm m để B có đúng hai tập con và B ⊂ A.
 Xem đáp án
Xem đáp án
Để B có đúng 2 tập con thì B có duy nhất một phần tử, và B ⊂ A nên B có một phần tử thuộc A.
Nên mx2 ‒ 4x + m ‒ 3 = 0 (1) có nghiệm duy nhất > 0.
m = 0 ta có phương trình: ‒4x ‒ 3 = 0 \[ \Leftrightarrow x = \frac{{ - 3}}{4}\] (loại).
m ≠ 0, Phương trình (1) có nghiệm duy nhất lớn hơn 0 khi:
∆’ = 4 ‒ m(m ‒ 3) = 0
⇔ m2 + 3m + 4 = 0 \[ \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = 4\end{array} \right.\]
Với m = 1 ta có: ‒x2 ‒ 4x ‒ 4 = 0 ⇔ x = ‒2 (loại).
Với m = 4 ta có: 4x2 ‒ 4x + 1 = 0
Phương trình có nghiệm \[x = \frac{1}{2} > 0\].
Vậy m = 4.
Câu 26:
Cho tứ giác ABCD (AB không song song với CD). Gọi M, N lần lượt là trung điểm của AB và CD biết \[MN = \frac{{BC + AD}}{2}\]. Chứng minh rằng: ABCD là hình thang.
 Xem đáp án
Xem đáp án
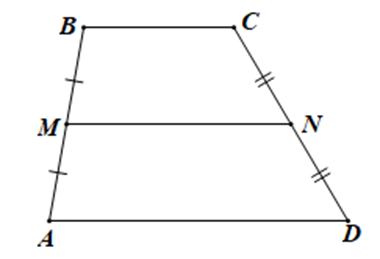
Gọi I là trung điểm của BD.
Vì I, N lần lượt là trung điểm của BD, CD
⇒ IN là đường trung bình của ∆DBC.
\[ \Rightarrow IN = \frac{{BC}}{2}\] và IN // BC.
Vì I, M lần lượt là trung điểm của BD, AB
⇒ IM là đường trung bình của ∆ABD.
\[ \Rightarrow IM = \frac{{AD}}{2}\]và IM // AD.
Vì \[MN = \frac{{BC + AD}}{2}\] nên MN = MI + IN
⇒ M, I, N thẳng hàng.
Mà IN // BC, IM // AD
Do đó, BC // AD ⇒ ABCD là hình thang.
Câu 27:
Chứng minh với mọi n ∈ ℤ ta có: \[\frac{1}{{2\sqrt 1 }} + \frac{1}{{3\sqrt 2 }} + \frac{1}{{4\sqrt 3 }} + ... + \frac{1}{{\left( {n + 1} \right)\sqrt n }} < 2\].
 Xem đáp án
Xem đáp án
Ta có: \(\frac{1}{{\left( {k + 1} \right)\sqrt k }} = \frac{{\sqrt k }}{{k\left( {k + 1} \right)}} = \sqrt k \left( {\frac{1}{k} - \frac{1}{{k + 1}}} \right)\)
\( = \sqrt k \left( {\frac{1}{{\sqrt k }} + \frac{1}{{\sqrt {k + 1} }}} \right)\left( {\frac{1}{{\sqrt k }} - \frac{1}{{\sqrt {k + 1} }}} \right)\)
\( = \left( {1 + \frac{{\sqrt k }}{{\sqrt {k + 1} }}} \right)\left( {\frac{1}{{\sqrt k }} - \frac{1}{{\sqrt {k + 1} }}} \right)\)
Do \(\frac{{\sqrt k }}{{\sqrt {k + 1} }} < 1 \Rightarrow 1 + \frac{{\sqrt k }}{{\sqrt {k + 1} }} < 2 \Rightarrow \frac{1}{{\left( {k + 1} \right)\sqrt k }} < 2\left( {\frac{1}{{\sqrt k }} - \frac{1}{{\sqrt {k + 1} }}} \right)\)
Áp dụng BĐT này, ta có: \(\frac{1}{2} < 2\left( {\frac{1}{1} - \frac{1}{{\sqrt 2 }}} \right)\)
\(\frac{1}{{3\sqrt 2 }} < 2\left( {\frac{1}{{\sqrt 2 }} - \frac{1}{{\sqrt 3 }}} \right)\)
\(\frac{1}{{\left( {n + 1} \right)\sqrt n }} < 2\left( {\frac{1}{{\sqrt n }} - \frac{1}{{\sqrt {n + 1} }}} \right)\)
Cộng tất cả các BĐT trên ta được:
\(\frac{1}{2} + \frac{1}{{3\sqrt 2 }} + \frac{1}{{4\sqrt 3 }} + \ldots + \frac{1}{{\left( {n + 1} \right)\sqrt n }} < 2\left( {\frac{1}{1} - \frac{1}{{\sqrt 2 }} + \frac{1}{{\sqrt 2 }} - \frac{1}{{\sqrt 3 }} + \ldots + \frac{1}{{\sqrt n }} - \frac{1}{{\sqrt {n + 1} }}} \right)\).
\(\; \Leftrightarrow \frac{1}{2} + \frac{1}{{3\sqrt 2 }} + \frac{1}{{4\sqrt 3 }} + \ldots + \frac{1}{{\left( {n + 1} \right)\sqrt n }} < 2\left( {1 - \frac{1}{{\sqrt {n + 1} }}} \right) < 2\) (đpcm).
Câu 28:
Chứng minh rằng mọi hàm số f(x) có tập xác định đối xứng, đều có thể viết dưới dạng tổng của một hàm số chẵn và một hàm số lẻ.
 Xem đáp án
Xem đáp án
Ta có:
\[f\left( x \right) = \frac{1}{2}\left[ {f\left( x \right) + f\left( { - x} \right)} \right] + \frac{1}{2}\left[ {f\left( x \right) - f\left( { - x} \right)} \right]\] với mọi x ∈ D.
Đặt \[{f_1}\left( x \right) = \frac{1}{2}\left[ {f\left( x \right) + f\left( { - x} \right)} \right]\], \[{f_2}\left( x \right) = \frac{1}{2}\left[ {f\left( x \right) - f\left( { - x} \right)} \right]\] với mọi x ∈ D.
Khi đó \[{f_1}\left( { - x} \right) = \frac{1}{2}\left[ {f\left( { - x} \right) + f\left( { - \left( { - x} \right)} \right)} \right] = \frac{1}{2}\left[ {f\left( { - x} \right) + f\left( x \right)} \right] = {f_1}\left( x \right)\] với mọi x ∈ D.
\[{f_2}\left( { - x} \right) = \frac{1}{2}\left[ {f\left( { - x} \right) - f\left( { - \left( { - x} \right)} \right)} \right] = \frac{1}{2}\left[ {f\left( { - x} \right) - f\left( x \right)} \right] = \frac{{ - 1}}{2}\left[ {f\left( x \right) - f\left( { - x} \right)} \right] = - {f_2}\left( x \right)\] với mọi x ∈ D.
Vậy f1(x) là hàm số chẵn, f2(x) là hàm số lẻ.
Câu 29:
Có bao nhiêu số tự nhiên có 10 chữ số đôi một khác nhau, trong đó các chữ số 1, 2, 3, 4, 5 được xếp theo thứ tự tăng dần từ trái qua phải và chữ số 6 luôn đứng trước chữ số 5.
 Xem đáp án
Xem đáp án
Gỉa sử số cần tìm có 10 chữ số khác nhau tương ứng với 10 vị trí.
Vì chữ ố 0 không đứng vị trí đầu tiên nên có 9 cách xếp vị trí cho chữ số 0 .
Có \[A_9^3\] cách xếp các chữ số 7; 8 ;9 vào 9 vị trí còn lại .
Vì chữ số 6 đứng trước chữ số 5 nên có 5 cách xếp vị trí cho chữ số 6 và 1 cách xếp cho các chữ số 1; 2; 3; 4; 5 theo thứ tự tăng dần. Theo quy tắc nhân \[9.5.A_9^3 = 22680\] số thoả mãn.
Câu 30:
Lúc đầu, số sách ngăn một bằng \(\frac{2}{3}\) số sách ngăn hai. Sau khi lấy ra ở mỗi ngăn 10 quyển sách thì số sách ngăn một bằng \(\frac{3}{5}\) số sách ngăn hai. Hỏi lúc đầu, cả hai ngăn có bao nhiêu quyển?
 Xem đáp án
Xem đáp án
Sau khi lấy ra ở mỗi ngăn 10 quyển thì hiệu số sách 2 ngăn không đổi.
Lúc đầu, số sách ngăn 1 chiếm:
\[\frac{2}{{3 - 2}} = 2\] (hiệu số sách)
Lúc sau, số sách ngăn 2 chiếm:
\[\frac{3}{{5 - 3}} = \frac{3}{2}\] (hiệu số sách)
10 quyển sách chiếm:
\[\frac{2}{1} - \frac{3}{2} = \frac{1}{2}\] (hiệu số sách)
Hiệu số sách 2 ngăn là:
10 : 1 × 2 = 20 (quyển)
Số sách ngăn 1 lúc đầu là:
20 × 2 = 40 (quyển)
Số sách ngăn 2 lúc đầu là:
40 + 20 = 60 (quyển)
Đáp số: Ngăn 1: 40 quyển sách;
Ngăn 2: 60 quyển sách.
Câu 31:
Một đội công nhân 9 người trong một ngày đắp được 60 mét đường. Người ta bổ sung thêm 18 người nữa cùng đắp thì trong một ngày đắp được bao nhiêu mét đường đó (mức đắp mỗi người như nhau)?
 Xem đáp án
Xem đáp án
Số người công nhân hiện có là:
9 + 18 = 27 (người)
27 người đắp được số đoạn đường là:
\[\frac{{27}}{9} \times 60 = 180\]
Đáp số: 180m.
Câu 32:
Một cửa hàng có 480 thùng hàng, mỗi thùng nặng 65kg. Cửa hàng đã bán được 300 thùng hàng. Số thùng hàng còn lại nặng bao nhiêu ki - lô -gam ?
 Xem đáp án
Xem đáp án
Số thùng hàng còn lại là:
480 ‒ 300 = 180 (thùng)
Số ki - lô - gam 180 thùng nặng là:
180 × 65 = 11700 (kg)
Đáp số: 11700 kg.
Câu 33:
Một hộ nông dân trồng đậu và cà trên diện tích 8a. Nếu trồng đậu thì cần 20 công và thu 3 000 000 đồng trên một a, nếu trồng cà thì cần 30 công và thu 40 000 000 đồng trên một a. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180?
 Xem đáp án
Xem đáp án
Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m2), điều kiện \(x \ge 0,y \ge 0\), ta có \(x + y \le 8\).
Số công cần dùng là \(20x + 30y \le 180\) hay \(2x + 3y \le 18\).
Số tiền thu được là
\(F = 3000000x + 4000000y{\rm{\;}}\)(đồng)
Hay \(F = 3x + 4y\) (triệu đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y \le 8}\\{2x + 3y \le 18}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\)
Sao cho \(F = 3x + 4y\) đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của \(\left( {\rm{H}} \right)\) ta được miền tứ giác \({\rm{OABC}}\) với \({\rm{A}}\left( {0;6} \right),{\rm{B}}\left( {6;2} \right)\), \(C\left( {8;0} \right)\) và \(O\left( {0;0} \right)\).
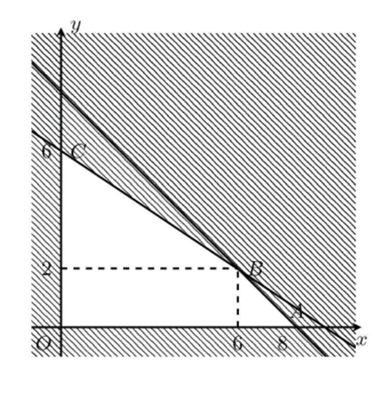
Xét giá trị của \({\rm{F}}\) tại các đỉnh \({\rm{O}},{\rm{A}},{\rm{B}},{\rm{C}}\) và so sánh ta suy ra \(x = 6,y = 2\) (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là \({\rm{F}} = 26\) (triệu đồng).
Đáp số: Trồng 6 (a) đậu, 2 (a) cà, thu hoạch 26 000 000 đồng.
Câu 34:
Nhân dịp lễ 20/10, shop thời trang Gumac giảm giá 40% cho các mặt hàng. Lan mua cái đầm hết 297 000 đồng. Tính giá tiền cái đầm trước khi giảm.
 Xem đáp án
Xem đáp án
297 000 đồng ứng với số phần trăm giá ban đầu của bộ quần áo là: 100% ‒ 40% = 60%
Giá ban đầu của bộ quần áo là: 297 000 : 60% = 495 000 (đồng)
Đáp số: 495 000 đồng.
Câu 35:
Giải phương trình \(\sqrt {{x^2} - 4x + 4} + 1 = 3x\).
 Xem đáp án
Xem đáp án
Ta có: \(\sqrt {{x^2} - 4x + 4} + 1 = 3x\)
\( \Leftrightarrow \sqrt {{{\left( {x - 2} \right)}^2}} = 3x - 1\)
\[ \Leftrightarrow \left| {x--2} \right| = 3x - 1\]
\( \Leftrightarrow \left\{ \begin{array}{l}3x - 1 \ge 0\\\left[ \begin{array}{l}x - 2 = 3x - 1\\x - 2 = - 3x + 1\end{array} \right.\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{3}\\\left[ \begin{array}{l}x = \frac{{ - 1}}{2}\\x = \frac{3}{4}\end{array} \right.\end{array} \right.\)
\( \Rightarrow x = \frac{3}{4}\).
Vậy phương trình có tập nghiệm là \(S = \left\{ {\frac{3}{4}} \right\}\).
Câu 36:
Tìm diện tích nhỏ nhất của các tam giác cân ngoại tiếp đường tròn bán kính r cho trước (tức đường tròn bán kính r nội tiếp tam giác cân).
 Xem đáp án
Xem đáp án
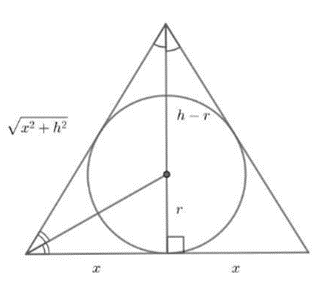
Ta có: \(\frac{{\sqrt {{x^2} + {h^2}} }}{x} = \frac{{h - r}}{r}{\rm{\;}} \Rightarrow 1 + \frac{{{h^2}}}{{{x^2}}} = {\left( {\frac{h}{r} - 1} \right)^2}\)
\( \Rightarrow \frac{h}{{{x^2}}} = \frac{h}{{{r^2}}} - \frac{2}{r}\)
\( \Rightarrow {x^2} = \frac{{h{r^2}}}{{h - 2r}}\)
\(S = hx \Rightarrow {S^2} = {(hx)^2} = \frac{{{h^3}{r^2}}}{{h - 2r}}\)
\( \Rightarrow \frac{1}{{{S^2}}} = \frac{{h - 2r}}{{{h^3}{r^2}}} = \frac{1}{{27{r^4}}} \cdot 27 \cdot \frac{r}{h} \cdot \frac{r}{h} \cdot \left( {1 - \frac{{2r}}{h}} \right)\)
\( \Rightarrow \frac{1}{{{S^2}}} \le \frac{1}{{27{r^4}}}{\left( {\frac{r}{h} + \frac{r}{h} + 1 - \frac{{2r}}{h}} \right)^3} = \frac{1}{{27{r^4}}}\)
\( \Rightarrow S'' \ge 3\frac{1}{3}{r^2}\).
Câu 37:
Trong mặt phẳng Oxy, cho đường thẳng d có phương trình (d): 3x + y – 2 = 0. Viết phương trình đường thẳng (d') là ảnh của d qua phép vị tự tâm O tỉ số \(\;k = \frac{{ - 1}}{2}\).
 Xem đáp án
Xem đáp án
Gọi \(M\left( {{x_0};{y_0}} \right)\) là 1 điểm thuộc \({\rm{d}} \Rightarrow 3{x_0} + {y_0} - 2 = 0\) (1)
Gọi M' là ảnh của \({\rm{M}}\) qua phép vị tự tâm O tỉ số k Þ M’ ∈ d’.
\(\left\{ {\begin{array}{*{20}{c}}{{x_{M'}} = k{x_M}}\\{{y_{M'}} = k{y_M}}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{M'}} = - \frac{1}{2}{x_0}}\\{{y_{M'}} = - \frac{1}{2}{y_0}}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_0} = - 2{x_{M'}}}\\{{y_0} = - 2{y_{M'}}}\end{array}} \right.\)
Thế vào (1): \(3.\left( { - 2{x_{M'}}} \right) - 2{y_{M'}} - 2 = 0\)
\( \Leftrightarrow 3{x_{M'}} + {y_{M'}} + 1 = 0\)
Vậy phương trình d' có dạng: \(3x + y + 1 = 0\).
Câu 38:
Tính giá trị lớn nhất của diện tích một tam giác biết 3 trong 2 cạnh của nó là 5 và 8.
 Xem đáp án
Xem đáp án
Giả sử AB = 5, AC=8.
Xét trường hợp \(\widehat {BAC}\) là góc nhọn:
Áp dụng công thức sau đây: \({S_{ABC}} = \frac{1}{2}.AB.AC.\sin \widehat {BAC}\)
Do \(\sin \widehat {BAC} < 1\) nên \({S_{ABC}} < \frac{{AB.AC}}{2}\).
Xét trường hợp \(\widehat {BAC}\) là góc tù.
Có công thức sau đây: \({S_{ABC}} = \frac{1}{2}.AB.AC.\sin \left( {{{180}^{\rm{o}}} - \widehat {BAC}} \right)\)
Lập luận tương tự vẫn có \({S_{ABC}} < \frac{{AB.AC}}{2}\).
Trường hợp \(\widehat {BAC}\) là góc vuông ta có: \({S_{ABC}} = \frac{1}{2}.AB.AC\)
Vậy giá trị lớn nhất của ∆ABC là: \({S_{ABC}} = \frac{1}{2}.AB.AC = \frac{{5.8}}{2} = 20\).
Câu 39:
Cho các tập hợp \(A = \left[ {1 - m;\frac{{m + 3}}{2}} \right]\) và B = (‒∞; ‒3) ∪ [3; +∞). Tìm tất cả các số thực m để A ∪ B = ℝ.
 Xem đáp án
Xem đáp án
Ta có: R ∖ B = (‒∞;+∞) ∖ {(‒∞; ‒3) ∪ [3; +∞)} = [‒3; 3)
Mà A ∪ B = ℝ ⇒ [‒3; 3) ⊂ \(A = \left[ {1 - m;\frac{{m + 3}}{2}} \right]\)
\( \Rightarrow \left\{ \begin{array}{l}1 - m \le 3\\3 \le \frac{{m + 3}}{2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}4 \le m\\6 \le m + 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}4 \le m\\3 \le m\end{array} \right.\)\( \Leftrightarrow m \ge 4\).
Câu 40:
Với giá trị nào của x thì đa thức dư trong mỗi phép chia sau có giá trị bằng: (x5 + 2x4 + 3x4 + x ‒ 3) : (x2 + 1)
 Xem đáp án
Xem đáp án
(x5 + 2x4 + 3x4 + x ‒ 3) : (x2 + 1)
\( = \frac{{{x^5} + {x^3} + 2{x^4} + 2{x^2} + 2{x^3} + 2x - 2x{}^2 - 2 - x - 1}}{{{x^2} + 1}}\)
\( = {x^3} + 2{x^2} + 2x - 2 + \frac{{ - x - 1}}{{{x^2} + 1}}\)
Để số dư là 0 thì ‒x ‒ 1 = 0 ⇔ x = ‒1.
Câu 41:
Cho tứ giác ABCD có hai góc đối ở đỉnh B và D cùng bằng 90°. Gọi O là trung điểm của AC. Chứng minh bốn điểm A, B, C, D cùng thuộc đường tròn đường kính AC.
 Xem đáp án
Xem đáp án
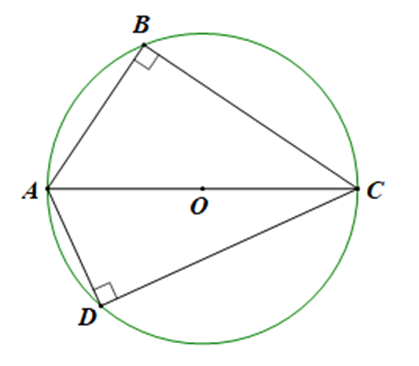
Xét ∆ABC có: \(\widehat {ABC} = {90^{\rm{o}}}\) (gt)
Suy ra AC là cạnh huyền.
Lại có: AO = OC (gt)
⇒ BO là đường trung tuyến ∆ABC
⇒ BO = AO = OC (đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền) (1)
Tương tự ta chứng minh được: DO = AO = OC (2)
Từ (1) và (2) ta có: BO = AO = OC = DO
Suy ra 4 điểm A, B, C, D cùng thuộc đường trong đường kính AC.
Câu 42:
Tứ giác có hai góc đối bằng 90° có phải là hình chữ nhật không?
 Xem đáp án
Xem đáp án
Tứ giác có 2 góc đối bằng 90° không có nghĩa tứ giác đấy là hình chữ nhật, vì tứ giác có 3 góc bằng 90° mới là hình chữ nhật.
Câu 43:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số có 5 chữ số khác nhau mà số đó nhất thiết có mặt các chữ số 1, 2, 5?
 Xem đáp án
Xem đáp án
Số có 5 chữ số khác nhau mà có 1, 2, 5 thì 2 chữ số còn lại lấy từ 4 chữ số 0, 3, 4, 6.
Lấy 2 số trong 4 số có \(C_2^4\) cách, trong đó có 3 trường hợp gồm 0; 3, 0; 4, 0; 6 .
Ba trường hợp trên giống nhau và có 3.4.4.3.2.1 = 288 số.
Ba trường hợp còn lại giống nhau và có 3.5! = 360 số.
Vậy có tất cả 288 + 360 = 648 số cần tìm.
Câu 44:
Từ các số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số có 3 chữ số khác nhau chia hết cho 3.
 Xem đáp án
Xem đáp án
Số chia hết cho 3 thì tổng các chữ số của số đó phải chia hết cho 3.
Ta có các bộ ba có tổng chia hết cho 3 là: (1; 2; 3), (1; 2; 6), (1; 3; 5), (1; 5; 6), (2; 3; 4), (2; 4; 6), (3; 4; 5), (4; 5; 6).
Mỗi bộ ba có 3! cách sắp xếp để được một số chia hết cho 3.
Vậy số các số có 3 chữ số khác nhau được lập từ các chữ số: 1; 2; 3; 4; 5; 6 chia hết cho 3 là: 8.3! = 48 (số).
