- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 5)
-
12891 lượt thi
-
63 câu hỏi
-
120 phút
Danh sách câu hỏi
Câu 1:
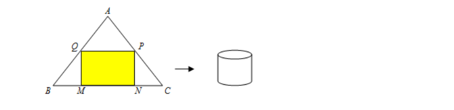
Bạn A muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác đều ABC có cạnh bằng 90(cm). Bạn muốn cắt mảnh tôn hình chữ nhật MNPQ từ mảnh tôn nguyên liệu để tạo thành hình trụ có chiều cao bằng MQ. Thể tích lớn nhất của chiếc thùng mà bạn A có thể làm được là.
 Xem đáp án
Xem đáp án
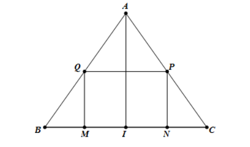
Gọi I là trung điểm của BC. Suy ra I là trung điểm của MN. Đặt
Khi đó ta có: Gọi R là bán kính của hình trụ
Thể tích của khối trụ là:
Xét với Suy ra
Do đó
Câu 2:
 Xem đáp án
Xem đáp án
Sử dụng tổng cấp số nhân, ta có công thức sau:
Trong đó với N là số tiền vay, là lãi suất hàng tháng), a là số tiền trả hàng tháng và n là số tháng.
Khi đó:
Vậy anh A mất 18 tháng thì sẽ trả hết nợ cho ngân hàng.
Câu 3:
Cho hình lập phương có độ dài bằng 1. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, và DD' Tính thể tích khối tứ diện MNPQ.
 Xem đáp án
Xem đáp án
Ta có hình vẽ sau:
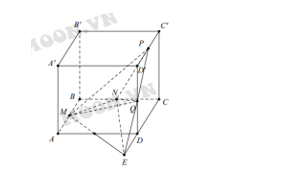
Khi đó ta có:
Do nên ta có:
Vì vậy
Câu 4:
Cho các hình sau thì có bao nhiêu hình là đa diện lồi?
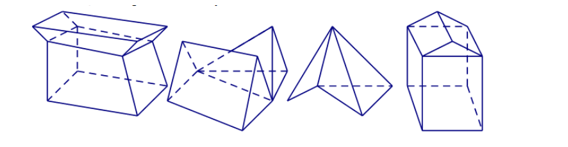
 Xem đáp án
Xem đáp án
Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kỳ của (H) luôn thuộc (H). Khi đó đa diện giới hạn (H) được gọi là đa diện lồi.
Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó.
Vậy theo định nghĩa trên thì chỉ có 1 hình là đa diện lồi.
Câu 5:
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, SA vuông góc với đáy, SA= a, I thuộc cạnh SB sao cho thuộc cạnh BC sao cho Tính thể tích khối tứ diện ACIJ ?
 Xem đáp án
Xem đáp án
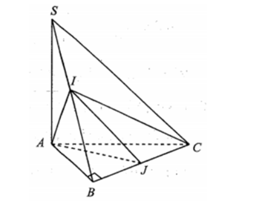
Do tam giác ABC vuông cân tại B nên ta có
Đồng thời do
Suy ra Mặt khác: (do J là trung điểm của BC).
Ta có:
Câu 6:
Cho hình lăng trụ đều ABC.A'B'C' Biết rằng góc giữa (A'BC) và (ABC) là Tam giác A'BC có diện tích bằng 8. Tính thể tích của khối lăng trụ ABC.A'B'C'.
 Xem đáp án
Xem đáp án
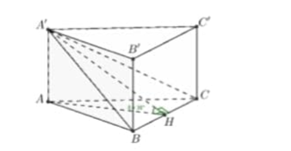
Gọi H là trung điểm của BC. Đặt AB= a ,ta có:
Xét tam giác A'AH ta tìm được:
Suy ra
Thể tích của khối lăng trụ ABC.
Câu 8:
Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y = |x3 – 3x2 – 9x + m| trên đoạn [– 2; 4] bằng 16. Số phần tử của S là:
 Xem đáp án
Xem đáp án
Xét hàm số f(x) = x3 – 3x2 – 9x + m trên đoạn [– 2; 4].
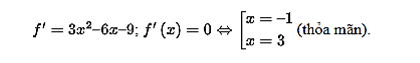
Ta có: f(– 2) = m – 2, f(– 1) = m + 5, f(3) = m – 27, f(4) = m – 20.
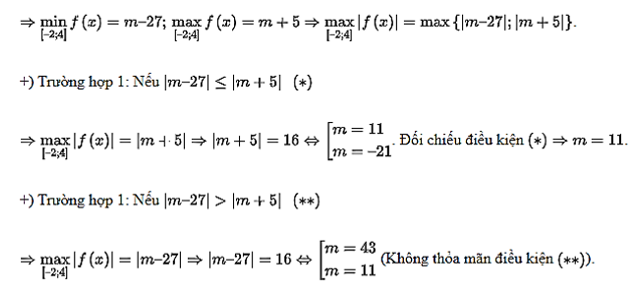
Vậy S = {11}. Do đó S có 1 phần tử.
Chọn đán án D
Câu 9:
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đồ thị hàm số có 5 điểm cực trị. Tổng tất cả các phần tử của tập S là.
 Xem đáp án
Xem đáp án
Ta có:
Để đồ thị hàm số đã cho có 5 điểm cực trị khi và chỉ khi phương trình: y'=0 có 5 nghiệm phân biệt. Điều này tương đương với Đặt phải có 3 nghiệm phân biệt khác 0 và 2.
Ta có: tức là ta cần đi tìm giá trị của m để đường thẳng y=m cắt đồ thị hàm số tại 3 điểm phân biêt
Do đó ta khảo sát hàm số thì ta có được:
Vậy Stổng tất cả các giá trị của S là 6.
Câu 10:
Đồ thị hàm số có bao nhiêu điểm cực tri?
 Xem đáp án
Xem đáp án
Xét hàm số Tập xác định D=R
Ta xét đạo hàm bậc nhất: Khi đó ta có BBT sau:
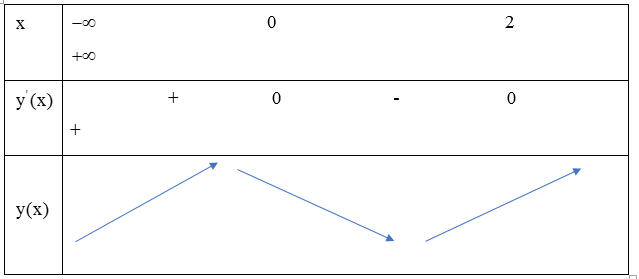
Hàm số là hàm số chẵn và đồ thị của nó được suy ra từ đồ thị hàm số bằng cách bỏ đi phần bên trái trục tung. Giữ nguyên phần bên phải trục tung và lấy đối xứng với phần bên phải Oy qua Oy. Như vậy ta sẽ thu được đồ thị hàm số có dạng sau:
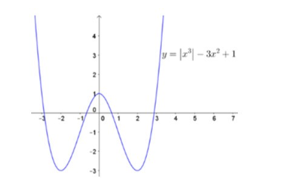
Vậy đồ thị hàm số có 3 điểm cực trị.
Câu 11:
Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng 2a, góc giữa hai đường thẳng AB' và BC' bằng Tính thể tích của khối lăng trụ đó.
 Xem đáp án
Xem đáp án
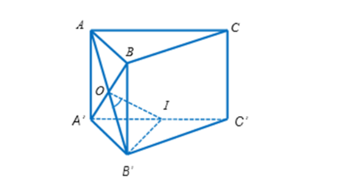
Gọi O là tâm của hình bình hành ABB'A' và I là trung điểm của A'C' Ta có:
Mặt khác nên là tam giác đều.
Suy ra
Vì ABC.A'B'C' là hình lăng trụ tam giác đều nên tam giác AA'B' vuông tại A' và có
Thể tích của khối lăng trụ đã cho là:
Câu 12:
Cho hình chóp đều S. ABCD có cạnh đáy bằng a, cạnh bên bằng 2a và O là tâm của đáy. Gọi M, N, P và Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB, SBC, SCD, SDA và ![]() là điểm đối xứng của S qua O. Tính thể tích của khối chóp S.MNPQ
là điểm đối xứng của S qua O. Tính thể tích của khối chóp S.MNPQ
 Xem đáp án
Xem đáp án
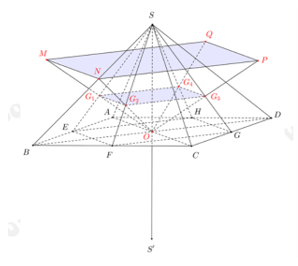
Gọi lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SDA.
Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Ta có:
Mặt khác:
Vậy thể tích của khối chóp S.MNPQ là:
Câu 13:
 Xem đáp án
Xem đáp án
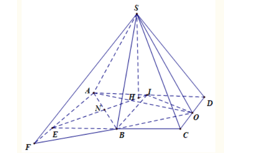
Gọi I, N là trung điểm của AD, AB. Gọi H là tâm đường tròn ngoại tiếp tam giác ABO, vì tam giác ABI đều nên H thuộc NI.
Kẻ HK vuông góc CD, dựng hình bình hành AECD. Gọi F là giao điểm của BO và AE.
Ta có: nên
Vì ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD, nên tam giác BIC và CID là các tam giác đều, do đó ta có:
Suy ra
Diện tích
Thể tích của khối chóp S. AFO là:
Diện tích tam giác SAF:
Vậy
Câu 14:
 Xem đáp án
Xem đáp án
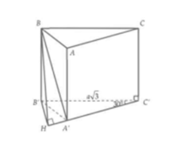
Ta có:
Mà
Vậy suy ra thể tích của khối lăng trụ đứng A'B'C' là:
Câu 15:
Cho G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án C.
Dựa vào đáp án ta có nhận xét: Xác định góc nên
Tương tự ta cũng xác định là góc ngoài của góc C nên
Xác định góc của do đó
Tương tự cho ý đáp án D, ta ra kết quả là
Câu 16:
Cho hình nón có thiết diện qua trục là tam giác đều. Gọi lần lượt là thể tích của khối cầu nội tiếp và nội tiếp hình nón đã cho. Tính tỉ số
 Xem đáp án
Xem đáp án
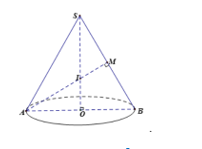
Giả sử cạnh của tam giác đều SAB bằng 1. Gọi thiết diện qua trục hình nón là tam giác đều SAB.
Gọi I là trọng tâm của tam giác đều SAB, khi đó I là tâm mặt cầu nội tiếp hình nón cũng là tâm mặt cầu ngoại tiếp hình nón.
Bán kính mặt cầu ngoại tiếp hình nón là:
Bán kính mặt cầu nội tiếp hình nón là:
Thể tích mặt cầu ngoại tiếp hình nón là:
Thể tích mặt cầu nội tiếp hình nón là:
Vậy
Câu 17:
Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?
 Xem đáp án
Xem đáp án
Gọi số tự nhiên có 6 chữ số đôi một khác nhau có dạng:
Sắp xếp cụm số 3, 4, 5 mà số 4 luôn đứng cạnh 3 và 5 thì ta có 2 cách sắp xếp: 345 và 543.
TH1: Nếu các cụm số 3, 4, 5 đứng đầu có các số tạo thành là: (số)
TH2: Nếu các cụm số 3,4,5 không đứng đầu có 3 cách sắp xếp là: x345xx; xx345x; xxx345.
Khi đó 3 chữ số còn lại có: cách chọn và sắp xếp.
Do đó ta có được các số tạo thành là: (số)
Áp dụng quy tắc cộng có: số thỏa mãn yêu cầu bài toán.
Câu 18:
Gọi A là tập các số tự nhiên có 6 chữ số đôi một khác nhau được tạo ra từ các chữ số 0, 1, 2, 3, 4, 5. Từ A chọn ngẫu nhiên một số. Tính xác suất để số được chọn có chữ số 3 và chữ số 4 đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Số cách lập số tự nhiên có 6 chữ số đôi một khác nhau từ tập A (không tính chữ số 0 đứng đầu) là: (số).
Số cách lập số tự nhiên có 6 chữ số đôi một khác nhau mà số 3 và số 4 đứng cạnh nhau là: (số).
Xác suất cần tìm thỏa mãn bài toán là:
Câu 19:
Từ các chữ số trong tập hợp X = {0; 1; 2; 3; 4; 5; 6} có thể lập được bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau có dạng abcdef sao cho: a+b = c+d = e+f?
 Xem đáp án
Xem đáp án
Ta có: 0 + 6 = 2 + 4 = 1 + 5
Suy ra a, b, c, d, e, f ∈ {0; 1; 2; 4; 5; 6}
+) a khác 0 nên a có 5 cách, b có 1 cách.
+) c khác a và b nên c có 4 cách, d có 1 cách.
+) e khác a, b, c, d nên e có 2 cách, d có 1 cách.
Do đó có 5.4.2 = 40 cách.
Ta lại có: 0 + 5 = 2 + 3 = 1 + 4
Do đó có 40 cách.
Vậy tổng cộng có 40 + 40 = 80 số.
Chọn D
Câu 20:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có Tính diện tích mặt cầu ngoại tiếp hình hộp đã cho.
 Xem đáp án
Xem đáp án
Gọi O là mặt cầu ngoại tiếp của hình hộp chữ nhật ABCD.A'B'C'D'.
Khi đó bán kính của hình hộp sẽ là:
Vậy diện tích của mặt cầu ngoại tiếp hình hộp là:
Câu 21:
Cho khối lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình bình hành có góc BAC bằng góc ACB bằng tam giác BCC' đều cạnh a, mặt phẳng vuông góc với đáy. Tính thể tích của khối lăng trụ đã cho.
 Xem đáp án
Xem đáp án
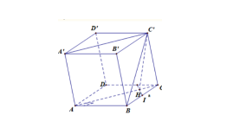
Do nên kẻ Do nên HB= HC
(với I là trung điểm của BC).
Ta có:
Tam giác C'HI vuông tại H nên ta có:
Tam giác vuông ABC có
Vậy thể tích của lăng trụ đã cho là:Câu 22:
Số cách chia 12 phần quà giống nhau cho 3 bạn sao cho ai cũng có ít nhất 2 phần quà.
 Xem đáp án
Xem đáp án
+ Chia trước cho mỗi học sinh một phần quà thì số phần quà còn lại là 9 phần quà.
+ Chia 9 phần quà cho 3 học sinh sao cho học sinh nào cũng có ít nhất một phần quà: Đặt 9 phần quà theo một hàng ngang, giữa các phần quà sẽ có 8 khoảng trống, chọn 2 khoảng trống trong 8 khoảng trống đó để chia 9 phần quà còn lại thành 3 phần quà mà mỗi phần có ít nhất một phần quà, có
+ Vậy tất cả có số cách chia là: (cách chia).
Câu 23:
Có bao nhiêu cách xếp 3 học sinh nam và 2 học sinh nữ thành một hàng sao cho 3 học sinh nam đứng cạnh nhau?
 Xem đáp án
Xem đáp án
Cho 3 học sinh nam cầm tay nhau coi như là một người, cùng với 2 học sinh nữ xếp thành một hàng ngang, có 3! cách.
Ba học sinh nam có thể đổi chỗ cho nhau, có 3! cách.
Vậy theo quy tắc nhân sẽ có: cách xếp.
Câu 24:
Từ một nhóm có 10 học sinh nam và 8 học sinh nữ. Có bao nhiêu cách chọn ra 5 học sinh trong đó có 3 bạn nam và 2 bạn nữ?
 Xem đáp án
Xem đáp án
B1: Số cách chọn ra 3 bạn nam trong 10 bạn nam là:
B2: Số cách chọn ra 2 bạn nữ trong 8 bạn nữ là:
B3: Áp dụng theo quy tắc nhân ta có số cách chọn ra 5 bạn thỏa mãn đề bài là:
Câu 25:
Từ các chữ số 0, 1, 2, 3, 4, 5, có thể lập bao nhiêu số gồm 3 chữ số khác nhau và chia hết cho 9.
 Xem đáp án
Xem đáp án
Gọi số cần lập có 3 chữ số đôi một khác nhau có dạng:
Theo giả thiết là các số này sẽ chia hết cho 9, do đó ta có:
Khi đó các số a, b, c thuộc các tập số và
+ TH1: Nếu các số a, b, c thuộc tập A.
Khi đó chữ số a có: 2 cách chọn; chữ số b có 2 cách và c có 1 cách chọn. Vậy ta có: (số).
+ TH2: Nếu các số a, b, c thuộc tập B.
Khi đó a có 3 cách chọn, b có 2 cách và c có 1 cách chọn. Vậy ta có: (số).
Áp dụng quy tắc cộng ta có các số tạo thành thỏa mãn bài toán là: (số).
Câu 26:
Từ các số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên mà mỗi số có 6 chữ số khác nhau và chữ số 2 đứng cạnh chữ số 3?
 Xem đáp án
Xem đáp án
Đặt xét số trong đó a; b; c; d; e đôi một khác nhau và thuộc tập {0; 1; y; 4; 5}.
Khi đó có 4 cách chọn a; 4 cách chọn b; 3 cách chọn c; 2 cách chọn d và 1 cách chọn e.
Theo quy tắc nhân có số.
Khi ta hoán vị trong y ta được hai số khác nhau.
Vậy có tất cả: số thỏa yêu cầu bài toán.
Câu 27:
Tính cosin góc tạo bởi cạnh bên và mặt đáy của hình chóp tứ giác đều có tất cả các cạnh bằng nhau.
 Xem đáp án
Xem đáp án
Gọi các cạnh của đáy ABCD đều có độ dài là a.
Vì chóp S. ABCD là chóp tứ giác đều, nên do đó ta có: SA=AB= a
Gọi O là tâm của hình vuông ABCD thì ta có:
Suy ra ta có:
Xét tam giác SAO vuông tại O ta có:
Câu 28:
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số có hai điểm cực trị nằm về hia phía của trục Ox.
 Xem đáp án
Xem đáp án
Đồ thị hàm số có 2 điểm cực trị nằm về hai phía của Ox
cắt trục Ox tại 3 điểm phân biệt.
có 3 nghiệm phân biệt.
Ta có:
Để (C) cắt trục Ox tại 3 điểm phân biệt khi và chỉ khi (1) có hai nghiệm phân biệt khác 2.
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện trên.
Câu 29:
Cho tam giác ABC, biết AB=8, AC=9, BC=11. Gọi M là trung điểm của BC, N là điểm trên đoạn AC sao cho Hãy khai triển theo
 Xem đáp án
Xem đáp án
Ta có:
Vậy
Câu 30:
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với đáy (ABCD). Gọi φ là góc giữa SD và mặt phẳng (ABCD). Tính cot φ?
 Xem đáp án
Xem đáp án
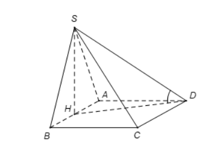
Gọi H là trung điểm của AB. Khi đó ta có nên hình chiếu của SD trên (ABCD) là HD.
Do đó
Mặt khác tam giác SAB đều cạnh a nên
Suy ra
Khi đó xét tam giác vuông SHD, ta có:
Câu 31:
Khối chóp S. ABCD có đáy là hình thoi cạnh a, cạnh SD thay đổi. Thể tích lớn nhất của khối chóp S. ABCD là bao nhiêu?
 Xem đáp án
Xem đáp án
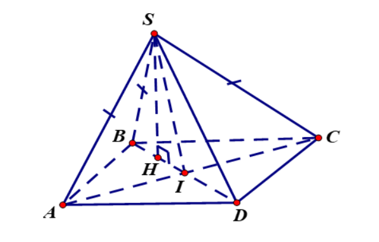
Gọi I là tâm của hình thoi ABCD, H là hình chiếu của S lên mặt (ABCD).
Ta có nên hình chiếu vuông góc của S xuống mặt phẳng (ABCD) trùng với tâm đường tròn ngoại tiếp tam giác ABC hay
Ta có:
Khi đó tam giác SBD vuông tại S. Giả sử SD=x. Ta có
Ta có:
Ta có:
Suy ra
Vậy
Câu 32:
Có bao nhiêu số nguyên dương không lớn hơn 2020 mà chia hết cho 2 hoặc cho 3?
 Xem đáp án
Xem đáp án
Số các số chia hết cho 2 là:
Số các số chia hết cho 3 là:
Số các số chia hết cho cả 2 và 3 (đồng nghĩa là chia hết cho 6) là:
Vậy các số thỏa mãn đề bài ra là:
Câu 33:
Phương trình có bao nhiêu nghiệm trên đoạn
 Xem đáp án
Xem đáp án
Vì nên ta có:
Mặt khác k là số nguyên nên k sẽ nhận các giá trị:
Vậy phương trình đã cho có 8 nghiệm trên đoạn
Câu 34:
Khối chóp tứ giác S. ABCD có đáy là hình bình hành. Có bao nhiêu mặt phẳng cách đều cả 5 điểm S, A, B, C, D?
 Xem đáp án
Xem đáp án
Có 5 mặt phẳng cách đều 5 điểm S, A, B, C, D. Cụ thể như sau:
+ Mặt phẳng đi qua 4 trung điểm của 4 cạnh bên: có 1 mặt.
+ Mặt phẳng đi qua tâm O và song song với từng mặt bên: có 4 mặt như vậy.
Câu 35:
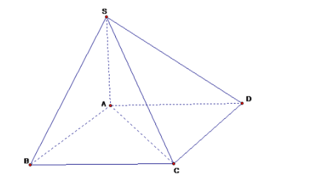
Khối chóp tứ giác S. ABCD có đáy là hình bình hành. Mặt phẳng (SAC) chia khối chóp S. ABCD thành mấy khối tứ diện.
 Xem đáp án
Xem đáp án
Mặt phẳng (SAC) chia khối chóp S. ABCD thành 2 khối tứ diện là S. ABC và S. ACD.
Câu 36:
Tứ diện đều có bao nhiêu trục đối xứng?
 Xem đáp án
Xem đáp án
Tứ diện đều có ba trục đối xứng đó là ba đường thẳng đi qua trung điểm của các cặp cạnh đối của nó.
Câu 37:
Gọi lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối lập phương. Tính các giá trị của
 Xem đáp án
Xem đáp án
Khối tứ diện đều có 3 trục đối xứng (đi qua trung điểm của các cặp cạnh đối diện) nên
Khối chóp tứ giác đều có 1 trục đối xứng (đi qua đỉnh và tâm của mặt tứ giác) nên
Khối lập phương có 9 trục đối xứng (Loại 1: đi qua tâm của các mặt đối diện; Loại 2: đi qua trung điểm các cặp cạnh đối diện) nên
Câu 40:
Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 sao cho số đó chia hết cho 15?
 Xem đáp án
Xem đáp án
Gọi số cần tìm có dạng Do N chia hết cho 15 nên N phải chia hết cho 3 và 5.
Vì vậy d có 1 cách chọn là bằng 5, và chia hết cho 3.
Do vai trò của các chữ số a, b, c là như nhau, mỗi số a, b và c có 9 cách chọn nên ta xét các trường hợp sau
TH1: Nếu chia hết cho 3, khi đó c chia hết cho 3 c có 3 cách chọn.
TH2: Nếu chia cho 3 dư 1, khi đó c chia 3 dư 2 c có 3 cách chọn.
TH3: Nếu chia cho 3 dư 2, khi đó c chia 3 dư 1 c có 3 cách chọn.
Vậy trong mọi trường hợp thì c đều có 3 cách chọn nên ta có tất cả số thỏa mãn.
Câu 42:
Lớp 11A1 có 41 học sinh trong đó có 21 bạn nam và 20 bạn nữ. Thứ hai đầu tuần lớp phải xếp hàng chào cờ thành một hàng dọc. Hỏi có bao nhiêu cách sắp xếp để 21 bạn nam xen kẽ với 20 bạn nữ?
 Xem đáp án
Xem đáp án
Vì số học sinh nam là lẻ nên bạn nam phải đứng đầu hàng.
Khi đó xếp 21 bạn nam vào 21 vị trí cố định có: (cách).
Sau đó ta xếp 20 bạn nữ vào 20 vị trí trống xen kẽ với các bạn nam thì sẽ có: (cách).
Vậy có tất cả số cách là: .
Câu 44:
Một hình trục có chiều cao bằng 6cm nội tiếp trong hình cầu có bán kính bằng 5cm. Thể tích khối trụ này bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Ta có hình vẽ sau:
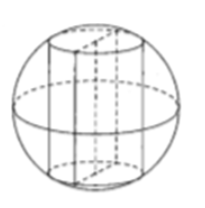
Bán kính đường tròn đáy của hình trụ là
Vậy thể tích của khối trụ cần tính là:
Câu 45:
 Xem đáp án
Xem đáp án
Ta sẽ phân tích vecto DM theo hai vecto DC và BC.
Vì ABCD là hình bình hành nên ta có:
Mặt khác M là trung điểm của AB nên
Suy ra
Câu 46:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số chẵn, mỗi số gồm 5 chữ số khác nhau trong đó có đúng 2 chữ số lẻ và 2 chữ số lẻ đó đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Gọi số cần tìm có dạng
+ TH1: 2 số lẻ liên tiếp ở vị trí ab. Khi đó: a có 3 cách chọn; b có 2 cách chọn; c có 4 cách chọn; d có 3 cách chọn và e có 2 cách chọn. Theo quy tắc nhân ta có: (số).
+ TH2: 2 số lẻ liên tiếp ở vị trí bc. Khi đó: a có 3 cách chọn; b có 3 cách chọn; c có 2 cách chọn; d có 3 cách chọn và e có 2 cách chọn. Theo quy tắc nhân ta có: (số).
+ TH3: 2 số lẻ liên tiếp ở vị trí cd (tượng tự TH2).
Vậy số cách chọn thỏa mãn yêu cầu đề bài là: (số).
Câu 47:
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).
b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.
c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α).
 Xem đáp án
Xem đáp án
a) Ta có:
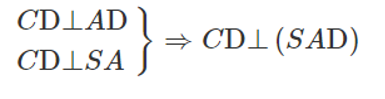
⇒ (SCD) ⊥ (SAD)
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
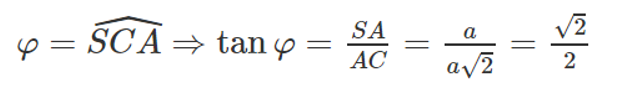
c)
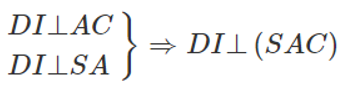
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và
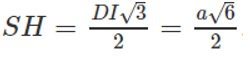 .
.Tam giác SDI có diện tích:
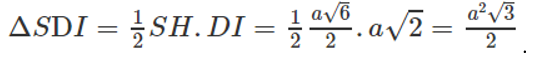
Câu 48:
Cho hình chóp S.ABC có SA=SB=SC=3, AC=2; ABC là tam giác vuông cân tại B. Tính thể tích V của khối chóp S.ABC.
 Xem đáp án
Xem đáp án
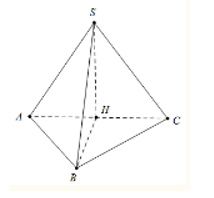
Ta có SA = SB = SC nên hình chiếu của đinh S xuống mặt phẳng (ABC) là tâm đường tròn ngoại tiếp tam giác ABC
Mà ABC là tam giác vuông cân tại B nên tâm đường tròn ngoại tiếp là trung điểm H của AC.
Ta có: Diện tích tam giác ABC là: .
Xét tam giác SAC, có: SH = .
Vậy thể tích hình chóp là: .
Câu 49:
Xét phép thử gieo một con xúc xắc cân đối, đồng chất hai lần. Số phần tử của không gian mẫu là?
 Xem đáp án
Xem đáp án
Số phần tử của không gian mẫu là:
Câu 50:
Xét phép thử T: “Gieo một con súc sắc cân đối và đồng chất” và biến cố A liên quan đến phép thử: “Mặt lẻ chấm xuất hiện”. Tính xác suất của biến cố A.
 Xem đáp án
Xem đáp án
Khi đó ta có:
Câu 51:
Tìm m để là phương trình bậc hai nhận là nghiệm.
 Xem đáp án
Xem đáp án
Ta có phương trình là phương trình bậc hai khi
Thay x= -2 ta được:
(thỏa mãn)
Vậy
Câu 52:
Tìm m để hàm số đồng biến trên R.
 Xem đáp án
Xem đáp án
Ta có
Hàm số đồng biến trên R khi và chỉ khi
Vậy m=1 là giá trị cần tìm thỏa mãn bài toán.
Câu 53:
Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có Tính diện tích tam giác ABC
 Xem đáp án
Xem đáp án
Xét bài toán: Tam giác ABC, điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là:
Ta có: Gọi G là giao điểm của hai trung tuyến BM, CN. Áp dụng công thức trung tuyến ta có:
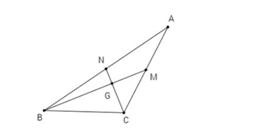
Áp dụng định lý Pythago cho tam giác vuông BGC, ta có:
Khi đó ta có:
Quay trở lại bài toán trên, xét tam giác ABC ta có:
Khi đó:
Câu 54:
Cho hàm số (với m là tham số thực). Với giá trị nào của m thì hàm số đã cho đồng biến trên R.
 Xem đáp án
Xem đáp án
Ta có:
Khi đó xét:
Để hàm số trên đồng biến trên R khi và chỉ khi với mọi giá trị của m là tham số thực.
Tức là:
Vậy
Câu 55:
Gọi m là giá trị nhỏ nhất của hàm số trên khoảng Tìm m.
 Xem đáp án
Xem đáp án
Hàm số liên tục trên
Ta có:
Bảng biến thiên của hàm số trên như sau:
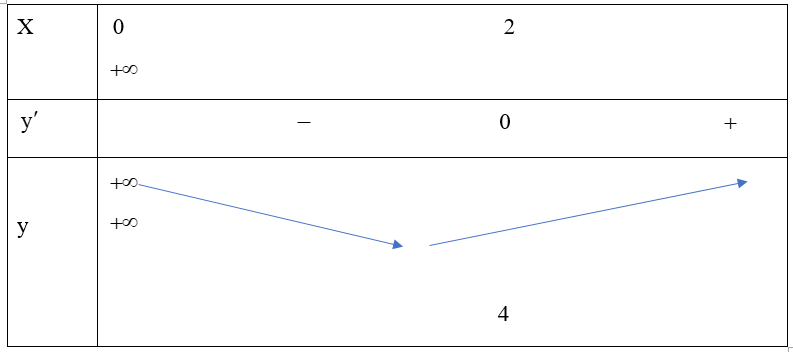
Dựa vào bảng biến thiên, suy ra ta có:
Nhắc lại:
Câu 56:
Với giá trị nào của m để phương trình có hai nghiệm thỏa mãn
 Xem đáp án
Xem đáp án
Xét phương trình đã cho tương đương với phương trình sau:
Đặt khi đó phương trình (1) trở thành:
Phương trình (1) có hai nghiệm là khi và chỉ khi phương trình (2) có hai nghiệm dương;
Theo định lý Viet ta có: Với khi đó ta có:
Câu 57:
Có hai giỏ đựng trứng là giỏ A và giỏ B, các quả trứng trong mỗi giỏ đều có hai loại là trứng lành và trứng hỏng. Tổng số trứng trong hai giỏ là 20 quả và số trứng giỏ A nhiều hơn số trứng giỏ B. Lấy ngẫu nhiên một quả trứng, biết xác suất để lấy được hai quả trứng lành là Tính số trứng lành trong giỏ A.
 Xem đáp án
Xem đáp án
Gọi a là số trứng lành, b là số trứng hỏng trong giỏ A.
Gọi x là số trứng lành, y là số trứng hỏng trong giỏ B.
Lấy ngẫu nhiên mỗi giỏ 1 quả trứng thì khi đó xác suất để lấy được 2 quả trứng lành là:
Do đó theo giả thiết bài toán ta có:
Vậy giỏ A có 11 quả trứng lành.
Câu 58:
Cho tam giác ABC, gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Số vectơ bằng vectơ MN có điểm đầu và điểm cuối trùng với một trong các điểm A, B, C, M, N, P là bao nhiêu vectơ?
 Xem đáp án
Xem đáp án
Do M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác ABC.
Suy ra
Lại có P là trung điểm của AB nên:
Từ (1) và (2) suy ra:
Vậy khi đó số vecto bằng mà có điểm đầu và cuối trùng với các điểm trên là:
Câu 59:
Cho khối lăng trụ tam giác đều ABC.A'B'C' Các mặt phẳng và (A'B'C') chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Tính giá trị của
 Xem đáp án
Xem đáp án
Gọi và Khi đó (ABC') và (A'B'C') chia khối lăng trụ đều ABC.A'B'C' thành 4 khối đa diện: và
Gọi V là thể tích của khối lăng trụ đều ABC.A'B'C' Ta có:
Mặt khác:
Suy ra
Do đó là thể tích lớn nhất của khối đa diện là thể tích nhỏ nhất của khối đa diện
Khi đó:
Câu 60:
Một hình chóp 16 cạnh thì có bao nhiêu mặt?
 Xem đáp án
Xem đáp án
Hình chóp có n cạnh bên và n cạnh đáy nên sẽ có 2n cạnh.
Khi đó ta có:
Vậy hình chóp 16 cạnh sẽ có 8 mặt bên và 1 mặt đáy nên tổng số là 9 mặt.
Câu 62:
Với các số a,b > 0 thỏa mãn Hãy chọn đẳng thức đúng sau:
 Xem đáp án
Xem đáp án
Ta có:
Lấy log của cả hai vế của đẳng thức trên thì ta có được:
Chọn đáp án B.
Câu 63:
Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương?
 Xem đáp án
Xem đáp án
Ta chia hình lập phương thành 6 khối tứ diện bằng nhau như sau:
+ Chia khối lập phương ABCD.A'B'C'D' thành hai khối lăng trụ tam giác bằng nhau: ABC.A'B'C' và BCD.B'C'D'
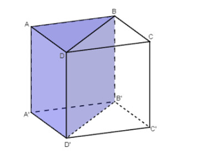
+ Tiếp theo, lần lượt chia khối lăng trụ ABD.A'B'D' và BCD.B'C'D' thành ba tứ diện: và
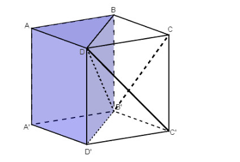
+ Ta chứng minh được các khối tứ diện này bằng nhau như sau:
- Hai khối tứ diện DABB' và DAA'B' bằng nhau vì chúng đối xứng nhau qua mặt phẳng (DAB')
- Hai khối tứ diện DAA'B' và DD'A'B' bằng nhau vì chúng đối xứng nhau qua mặt phẳng (B'A'D)
Từ (1) và (2) suy ra ba khối tứ diện và DD'A'B' bằng nhau.
- Tương tự, ba khối tứ diện cũng bằng nhau.
Vậy khối lập phương ABCD.A'B'C'D' được chia thành sáu khối tứ diện bằng nhau.