- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 42)
-
12943 lượt thi
-
47 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Lời giải
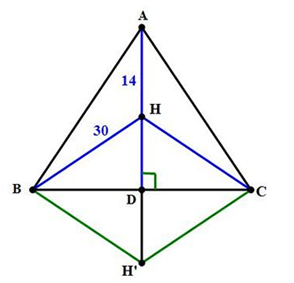
Gọi H’ là điểm đối xứng H qua BC.
Suy ra D là trung điểm của HH’
Vì tam giác ABC cân tại A, AD là đường cao nên AD là trung tuyến
Suy ra D là trung điểm của BC
Xét tứ giác BHCH’ có
D là trung điểm của HH’ và BC;
BC và HH’ là hai đường chéo
Suy ra BHCH’ là hình bình hành.
Mà BH = CH nên hình bình hành BHCH’ là hình thoi
Do đó BH’ // CH, BH = BH’.
Lại có CH ⊥ AB (vì H là trực tâm của tam giác ABC) nên BH’⊥ AB
Hay tam giác ABH’ vuông tại B
Mà BD ⊥ AH’
Suy ra H’B2 = H’D . H’A
⇔ HB2 = HD . (2HD + HA)
⇔ 302 = HD . (2HD + 14)
⇔ 2HD2 + 14HD – 900 = 0
⇔ (HD + 25)(HD – 18) = 0
⇔ HD – 18 = 0 (vì HD > 0)
⇔ HD = 18
Ta có AD = AH + HD = 14 + 18 = 32 cm
Vậy AD = 32 cm.
Câu 2:
Cho tứ giác MNPQ gọi R, S, T, V theo tứ tự là trung điểm của MN, NP, PQ, QM.
a) Chứng minh rằng RSTV là hình bình hành.
b) Nếu MP vuông góc với NQ thì RQTV là hình gì?
 Xem đáp án
Xem đáp án
Lời giải
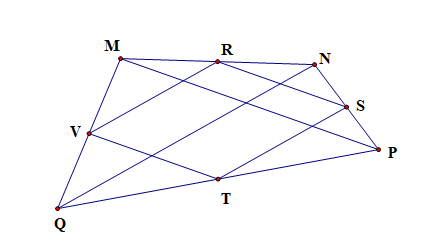
• Xét ΔMNQ có: R, V lần lượt là trung điểm của MN, MQ
Do đó RV là đường trung bình của ΔMNQ
Suy ra RV // NQ và \(RV = \frac{1}{2}NQ\) (1)
• Xét ΔNPQ có: T, S lần lượt là trung điểm của QP, NP
Do đó TS là đường trung bình của ΔNPQ
Suy ra TS // NQ và \(T{\rm{S}} = \frac{1}{2}NQ\) (2)
Từ (1) và (2) suy ra RV // TS và RV = TS
Do đó RSTV là hình bình hành.
b) Xét ΔMNP có: R, S lần lượt là trung điểm MN, NP
Suy ra RS là đường trung bình của ΔMNP
Do đó RS // MP
Mà MP ⊥ NQ, nên RS ⊥ NQ (quan hệ từ vuông góc đến song song)
Lại có ST // NQ
Suy ra RS ⊥ ST hay \(\widehat {RST} = 90^\circ \).
Xét hình bình hành RSTV có \(\widehat {RST} = 90^\circ \)
Suy ra RSTV là hình chữ nhật
Vậy nếu MP vuông góc với NQ thì RQTV là hình chữ nhật.
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \(4 - 2\sqrt 3 = 3 - 2\sqrt 3 + 1 = {\left( {\sqrt 3 } \right)^2} - 2\sqrt 3 .1 + {1^2} = {\left( {\sqrt 3 - 1} \right)^2}\)
Vậy \({\left( {\sqrt 3 - 1} \right)^2} = 4 - 2\sqrt 3 \).
Câu 4:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: B
Ta có

Vậy ta chọn đáp án B.
Câu 5:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \[{\rm{co}}{{\rm{s}}^2}x + {\rm{co}}{{\rm{s}}^2}2x + {\rm{co}}{{\rm{s}}^2}3x + {\rm{co}}{{\rm{s}}^2}4x = \frac{3}{2}\]
\[ \Leftrightarrow {\rm{2co}}{{\rm{s}}^2}x + 2{\rm{co}}{{\rm{s}}^2}2x + 2{\rm{co}}{{\rm{s}}^2}3x + 2{\rm{co}}{{\rm{s}}^2}4x - 3 = 0\]
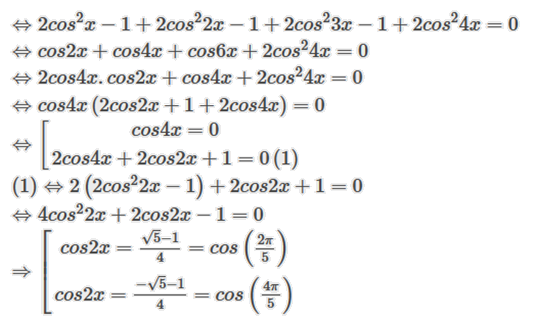
\( \Leftrightarrow \left[ \begin{array}{l}2{\rm{x}} = \frac{{2\pi }}{5} + k2\pi \\2{\rm{x}} = \frac{{4\pi }}{5} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = \frac{\pi }{5} + k\pi \\{\rm{x}} = \frac{{2\pi }}{5} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Ta có cos4x = 0 \( \Leftrightarrow 4{\rm{x}} = \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow {\rm{x}} = \frac{\pi }{8} + \frac{{k\pi }}{4}\,\,\,\left( {k \in \mathbb{Z}} \right)\)
Vậy \[{\rm{x}} \in \left\{ {\frac{\pi }{8} + \frac{{k\pi }}{4};\frac{\pi }{5} + k\pi ;\frac{{2\pi }}{5} + k\pi } \right\},k \in \mathbb{Z}\].
Câu 6:
 Xem đáp án
Xem đáp án
Lời giải
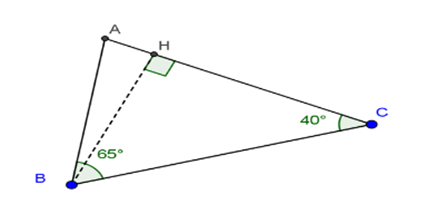
Xét tam giác ABC có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat A = 180^\circ - \widehat B - \widehat C = 180^\circ - 65^\circ - 40^\circ = 75^\circ \)
Áp dụng định lý sin cho tam giác ABC ta có
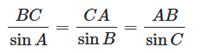
Hay \(\frac{{4,2}}{{\sin 75^\circ }} = \frac{{CA}}{{\sin 65^\circ }} = \frac{{AB}}{{\sin 40^\circ }}\)
Suy ra \(AC = \frac{{4,2.\sin 60^\circ }}{{\sin 75^\circ }} \approx 3,76\) (cm)
\(AB = \frac{{4,2.\sin 40^\circ }}{{\sin 75^\circ }} \approx 2,79\) (cm)
Vậy AB ≈ 2,79 cm, AC ≈ 3,76 cm và \(\widehat A = 75^\circ .\)
Câu 7:
 Xem đáp án
Xem đáp án
Lời giải
• Phương trình hoành độ giao điểm của (d1) và (d2) là
– x + 1 = x + 1
⇔ x + x = 1 – 1
⇔ 2x = 0
⇔ x = 0
Suy ra y = – 0 + 1 = 1.
Vậy A(0; 1) là tọa độ giao điểm của (d1) và (d2).
• Phương trình hoành độ giao điểm của (d2) và (d3) là
x + 1 = – 1
⇔ x = – 1 – 1
⇔ x = – 2
Suy ra y = – 1
Vậy B(–2; –1) là tọa độ giao điểm của (d2) và (d3).
• Phương trình hoành độ giao điểm của (d1) và (d3) là
– x + 1 = – 1
⇔ x = 1 + 1
⇔ x = 2
Suy ra y = – 1
Vậy C(2; –1) là tọa độ giao điểm của (d1) và (d3).
Câu 8:
 Xem đáp án
Xem đáp án
Lời giải
Ta có sin2x – cosx + 1 = 0
⇔ 1 – cos2x – cosx + 1 = 0
⇔ cos2x + cosx – 2 = 0
⇔ (cosx + 2)(cosx – 1) = 0
⇔ cosx – 1 = 0 (vì cosx + 2 > 0 với mọi x)
⇔ cosx = 1
⇔ x = k2π (k ∈ ℤ).
Vậy x = k2π (k ∈ ℤ).
Câu 9:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Ta có nhận xét sau:
10° + 80° = 20° + 70° = 30° + 60° = 40° + 50° = 90°
Nên các cung lượng giác tương ứng đôi một phụ nhau
Do các góc phụ nhau thì sin góc này bằng cosin góc kia nên ta có:
P = (sin2 10° + sin2 80°) + (sin2 20° + sin2 70°) + ...+ (sin2 40° + sin2 50°)
= (sin2 10° + cos2 10°) + (sin2 20° + cos2 20°) + ...+ (sin2 40° + cos2 40°)
= 1 + 1 + 1 + 1 = 4.
Vậy ta chọn đáp án C.
Câu 10:
 Xem đáp án
Xem đáp án
Lời giải
Ta có sin2x = 1
\[ \Leftrightarrow \left[ \begin{array}{l}{\mathop{\rm s}\nolimits} {\rm{inx}} = 1\\{\mathop{\rm s}\nolimits} {\rm{inx}} = - 1\end{array} \right.\]
\[ \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = \frac{\pi }{2} + k2\pi \\{\rm{x}} = - \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]
Vậy \[{\rm{x}} = \frac{\pi }{2} + k2\pi \] hoặc \[{\rm{x}} = - \frac{\pi }{2} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\].
Câu 11:
Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm.
a) Tính số đo góc B, góc C (làm tròn đến độ) và đường cao AH.
b) Chứng minh rằng AB. cos B + AC . cosC = BC.
c) Trên cạnh AC lấy điểm D sao cho DC = 2DA. Vẽ DE vuông góc với BC tại E. Chứng minh rằng \(\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{4}{{9D{E^2}}}\).
 Xem đáp án
Xem đáp án
Lời giải
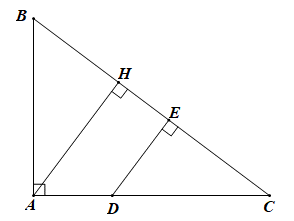
a) Vì tam giác ABC vuông tại A nên AB2 + AC2 = BC2 (định lí Pytago)
Hay 62 + 82 = BC2, suy ra BC = 10 (cm).
Xét tam giác ABC có \[\sin B = \frac{{AC}}{{BC}} = \frac{8}{{10}} = \frac{4}{5}\], suy ra \(\widehat B \approx 53^\circ \)
Vì tam giác ABC vuông tại A nên \(\widehat B + \widehat C = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat C = 90^\circ - \widehat B \approx 90^\circ - 53^\circ = 37^\circ \)
Xét tam giác ABC vuông tại A có đường cao AH
Suy ra AH . BC = AB . AC (hệ thức lượng trong tam giác vuông)
Hay AH . 10 = 6 . 8
Suy ra AH = 4,8 cm.
b) Vì tam giác ABH vuông tại H nên BH = AB . cosB
Vì tam giác ACH vuông tại H nên CH = AC . cosC
Ta có BC = CH + BH = AC . cosC + AB . cosB.
c) Xét tam giác ABC vuông tại A có AH ⊥ BC
Suy ra \(\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{A{H^2}}}\) (hệ thức lượng trong tam giác vuông) (1)
Ta có AH ⊥ BC, DE ⊥ BC nên AH // DE (quan hệ từ vuông góc đến song song)
Suy ra \(\frac{{DE}}{{AH}} = \frac{{C{\rm{D}}}}{{AC}} = \frac{2}{3}\) (vì CD = 2AD)
Suy ra \(\frac{{D{E^2}}}{{A{H^2}}} = \frac{4}{9}\)
Do đó \(\frac{1}{{A{H^2}}} = \frac{4}{{9D{E^2}}}\) (2)
Từ (1) và (2) suy ra \(\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{4}{{9D{E^2}}}\)
Vậy \(\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{4}{{9D{E^2}}}\).Câu 12:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: B
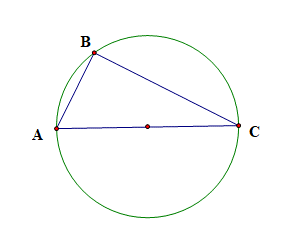
Áp dụng định lí Cosin, ta có
BC2 = AB2 + AC2 – 2AB . AC . cosA = 32 + 62 – 2 . 3 . 6 . cos60° = 27
Ta thấy: BC2 + AB2 = 27 + 9 = 36 = 62 = AC2
Suy ra tam giác ABC vuông tại B
Do đó bán kính đường tròn ngoại tiếp tam giác ABC là
R = AC : 2 = 3
Vậy ta chọn đáp án B.
Câu 13:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
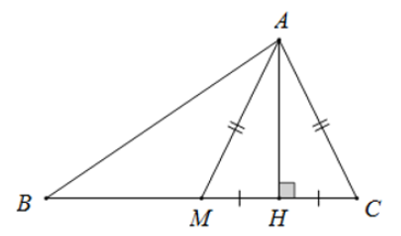
Gọi H là trung điểm của MC
Suy ra MH = HC
Vì M là trung điểm của BC nên BM = MC = 2HC
Ta có \(\frac{{CH}}{{BH}} = \frac{{CH}}{{BM + MH}} = \frac{{CH}}{{2CH + CH}} = \frac{{CH}}{{3CH}} = \frac{1}{3}\)
Vì AM = AC (giả thiết) nên tam giác AMC cân tại A
Mà AH là trung tuyến
Suy ra AH là đường cao
Khi đó \(\frac{{\tan B}}{{\tan C}} = \frac{{AH}}{{BH}}:\frac{{AH}}{{CH}} = \frac{{CH}}{{BH}} = \frac{1}{3}\)
Vậy ta chọn đáp án A.
Câu 14:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Số ngỗng chiếm số phần là
\(1 - \frac{3}{5} - \frac{1}{6} = \frac{{30 - 18 - 5}}{{30}} = \frac{7}{{30}}\) (tổng số con)
Ta có \(\frac{1}{6} < \frac{7}{{30}} < \frac{3}{5}\)
Suy ra số ngỗng trong trang trại nhiều hơn số vịt
Vậy ra chọn đáp án C.
Câu 15:
 Xem đáp án
Xem đáp án
Lời giải
Gọi số cần tìm là \[\overline {ab} \]
Theo đề bài ta có \[\overline {ab6} = \overline {ab} {\rm{ }} + 537\]
\( \Leftrightarrow \overline {ab0} + 6 = \overline {ab} + 537\)
\( \Leftrightarrow \overline {ab} \times 10 - \overline {ab} = 537 - 6\)
\( \Leftrightarrow \overline {ab} \times 9 = 531\)
\( \Leftrightarrow \overline {ab} = 531:9\)
\( \Leftrightarrow \overline {ab} = 59\)
Vậy số cần tìm là 59.
Câu 16:
 Xem đáp án
Xem đáp án
Lời giải
Thay x = 2 vào phương trình ta có
22 – 3(m – 1) . 2 + 2m – 4 = 0
⇔ 4 – 6m + 6 + 2m – 4 = 0
⇔ 6 – 4m = 0
⇔ \(m = \frac{3}{2}\)
Thay \(m = \frac{3}{2}\) vào phương trình ta có
\[{{\rm{x}}^2} - 3\left( {\frac{3}{2} - 1} \right)x + 2.\frac{3}{2} - 4 = 0\]
⇔ \[{{\rm{x}}^2} - \frac{3}{2}x - 1 = 0\]
⇔ 2x2 – 3x – 2 = 0
⇔ (x – 2)(2x + 1) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\2{\rm{x}} + 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = \frac{{ - 1}}{2}\end{array} \right.\)
Vậy \(m = \frac{3}{2}\) thỏa mãn yêu cầu đề bài và nghiệm còn lại là \[{\rm{x}} = \frac{{ - 1}}{2}\].
Câu 17:
Phân tích đa thức thành nhân tử
a) x2 – 25 + y2 + 2xy;
b) x2 – 2x – 4y2 – 4y;
c) 16x3 + 0,25y3z3;
d) x3 – x2 – x + 1;
e) x4 + x3 + x2 – 1;
f) x4 + 6x2y + 9y2 – 1;
g) x2 + 4x – y2 + 4;
h) x3 + 3x2 – 3x – 1.
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
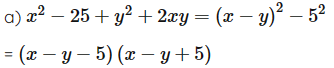
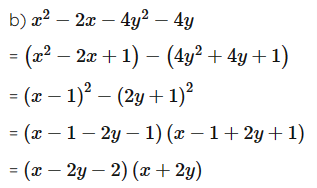
c)
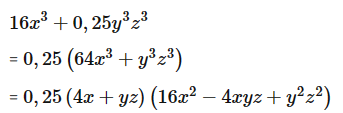
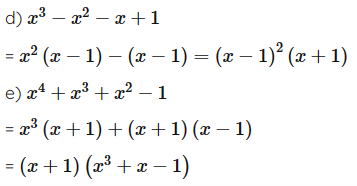
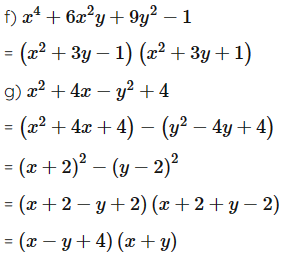
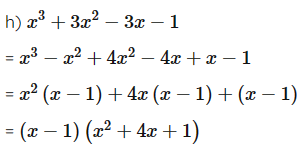
Câu 18:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \(\left( {{\rm{x}} + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 1\)
\( \Leftrightarrow \left( {\sqrt {{x^2} + 1} - x} \right)\left( {{\rm{x}} + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = \sqrt {{x^2} + 1} - x\)
\( \Leftrightarrow \left( {{x^2} + 1 - {x^2}} \right)\left( {y + \sqrt {{y^2} + 1} } \right) = \sqrt {{x^2} + 1} - x\)
\( \Leftrightarrow y + \sqrt {{y^2} + 1} = \sqrt {{x^2} + 1} - x\) (1)
Ta có \(\left( {{\rm{x}} + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 1\)
\( \Leftrightarrow \left( {\sqrt {{x^2} + 1} - x} \right)\left( {y + \sqrt {{y^2} + 1} } \right)\left( {\sqrt {{y^2} + 1} - y} \right) = \sqrt {{y^2} + 1} - y\)
\( \Leftrightarrow \left( {\sqrt {{x^2} + 1} - x} \right)\left( {{y^2} + 1 - {y^2}} \right) = \sqrt {{y^2} + 1} - y\)
\( \Leftrightarrow \sqrt {{x^2} + 1} - x = \sqrt {{y^2} + 1} - y\)
\( \Leftrightarrow \sqrt {{y^2} + 1} - y = \sqrt {{x^2} + 1} - x\) (2)
Trừ vế theo vế của (1) cho (2) ta được
2y = 0
Û y = 0
Thay y = 0 vào (1) ta được \(1 = \sqrt {{x^2} + 1} - x\)
\( \Leftrightarrow \sqrt {{x^2} + 1} = x + 1\)
\( \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\{x^2} + 1 = {\left( {x + 1} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\{x^2} + 1 = {x^2} + 2x + 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\2x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\x = 0\end{array} \right. \Leftrightarrow x = 0\)
Do đó x + y = 0 + 0 = 0.
Vậy x + y = 0.
Câu 19:
 Xem đáp án
Xem đáp án
Lời giải
Thay \(x = \frac{{ - 1}}{2}\) vào biểu thức A ta có
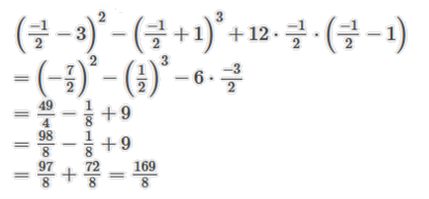
Vậy \[{\rm{A}} = \frac{{169}}{8}.\]
Câu 20:
 Xem đáp án
Xem đáp án
Lời giải
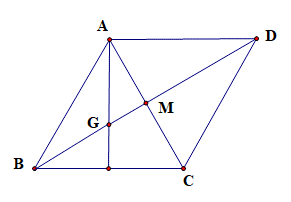
Gọi G là trọng tâm tam giác ABC
Khi đó \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Dựng hình bình hành ABCD ta có \(\overrightarrow {BA} = \overrightarrow {C{\rm{D}}} \)
Ta có \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow {C{\rm{D}}} + \overrightarrow {MC} = \overrightarrow {M{\rm{D}}} \)
Khi đó \(T = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| + 3\left| {\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} } \right| = 3\overrightarrow {MG} + 3\overrightarrow {M{\rm{D}}} \ge 3\overrightarrow {G{\rm{D}}} \)
(vì G và D nằm khác phía với đường thẳng AC)
Dấu “=” xảy ra khi M là giao điểm của DG và AC
Hay M là trung điểm của AC
Mà ABCD là hình bình hành
Suy ra M là trung điểm của BD
Do đó MB = MD
Vì tam giác ABC đều có BM là trung tuyến
Nên BM là đường cao
Hay tam giác BCM vuông tại M
Suy ra \(BM = \sqrt {B{C^2} - C{M^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
Suy ra \(DM = \frac{{a\sqrt 3 }}{2}\)
Vì G là trọng tâm của tam giác ABC nên \[GM = \frac{1}{3}BM = \frac{{a\sqrt 3 }}{6}\]
Ta có DG = DM + GM
Hay \[DG = \frac{{a\sqrt 3 }}{2} + \frac{{a\sqrt 3 }}{6} = \frac{{2\sqrt 3 a}}{3}\]
Vậy giá trị nhỏ nhất của T là \(2\sqrt 3 a\) khi M là trung điểm của AC.
Câu 21:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \(P = \frac{4}{x} + \frac{1}{{4y}} = \frac{4}{x} + 4{\rm{x}} + \frac{1}{{4y}} + 4y - 4\left( {x + y} \right)\)
Áp dụng bất đẳng thức Cô – si ta có
\(\frac{4}{x} + 4{\rm{x}} \ge 2\sqrt {\frac{4}{x}.4{\rm{x}}} = 8\)
\(\frac{1}{{4y}} + 4y \ge 2\sqrt {\frac{1}{{4y}}.4{\rm{y}}} = 2\)
Suy ra \(P \ge 8 + 2 - 4.\frac{5}{4} = 5\)
Vậy giá trị nhỏ nhất của P là 5 khi \(\left\{ \begin{array}{l}\frac{4}{x} = 4{\rm{x}}\\\frac{1}{{4y}} = 4y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = \frac{1}{4}\end{array} \right.\).
Câu 22:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \(n\left( \Omega \right) = C_{11}^3 = 165\)
Gọi A là biến cố “Chọn ngẫu nhiên 3 số từ tập S sao cho tổng 3 số là 12”
A = {(1, 2, 9); (1, 3, 8); (1, 4, 7); (1, 5, 6); (2, 3, 7); (2, 4, 6); (3, 4, 5)}.
Suy ra n(A) = 7.
Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{7}{{165}}.\)
Câu 23:
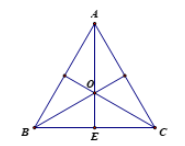
Cho tam giác ABC đều cạnh a, tâm O. Hãy tính:
a) \(\overrightarrow {AB} .\overrightarrow {AC} \).
b) \(\overrightarrow {AB} .\overrightarrow {BC} \).
c) \(\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right)\).
d) \(\left( {\overrightarrow {AB} + 2\overrightarrow {AC} } \right)\left( {\overrightarrow {AB} - 3\overrightarrow {BC} } \right)\).
 Xem đáp án
Xem đáp án
Lời giải
a) Ta có
\(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.c{\rm{os}}\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = AB.AC.c{\rm{os}}\widehat {BAC} = a.a.c{\rm{os60}}^\circ = \frac{{{a^2}}}{2}\).
b) Ta có
\(\overrightarrow {AB} .\overrightarrow {BC} = - \overrightarrow {BA} .\overrightarrow {BC} = - BA.BC.cos\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = - BA.BC.co{\rm{s60}}^\circ {\rm{ = }}\frac{{ - {a^2}}}{2}\).
c) Gọi E là trung điểm của BC.
Suy ra \(\overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {OE} \).
Ta có \(\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right)\)
\( = 2\overrightarrow {OE} .\overrightarrow {CB} \)
\( = 2{\rm{O}}E.CB.co{\rm{s}}\left( {\overrightarrow {OE} ,\overrightarrow {CB} } \right)\)
\( = 2{\rm{O}}E.CB.\cos 90^\circ = 0\).
d) Ta có \(\overrightarrow {AC} .\overrightarrow {BC} = \overrightarrow {AC} .\overrightarrow {BC} = AC.BC.cos\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = AC.BC.co{\rm{s60}}^\circ {\rm{ = }}\frac{{{a^2}}}{2}\)
Ta có \(\left( {\overrightarrow {AB} + 2\overrightarrow {AC} } \right)\left( {\overrightarrow {AB} - 3\overrightarrow {BC} } \right)\)
\( = {\overrightarrow {AB} ^2} - 3\overrightarrow {AB} .\overrightarrow {BC} + 2\overrightarrow {AB} .\overrightarrow {AC} - 6\overrightarrow {AC} .\overrightarrow {BC} \)
\( = {a^2} + \frac{{3{{\rm{a}}^2}}}{2} + {a^2} - 3{{\rm{a}}^2} = \frac{{{a^2}}}{2}\).
Câu 24:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
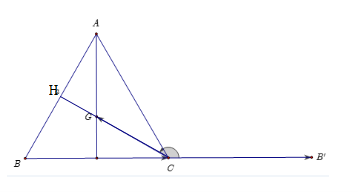
Vì tam giác ABC đều cạnh a nên AB = BC = AC = a và \(\widehat {ACB} = 60^\circ \)
Vì tam giác ABC đều có G là trọng tâm nên G là giao điểm của ba đường phân giác
Suy ra CG là tia phân giác của \(\widehat {ACB}\)
Do đó \(\widehat {BCG} = \frac{1}{2}\widehat {ACB} = \frac{1}{2}.60^\circ = 30^\circ \)
Gọi CB’ là tia đối của tia BC
Góc tạo bởi \(\overrightarrow {BC} ,\overrightarrow {CG} \) là \(\widehat {B'CG}\)
Ta có \(\widehat {B'CG} + \widehat {BCG} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {B'CG} = 180^\circ - 30^\circ = 150^\circ \)
Gọi H là giao điểm của CG và AB
Khi đó CH ⊥ AB và H là trung điểm của AB
Hay tam giác ACH vuông tại H
Suy ra \(CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
Do đó \(CG = \frac{2}{3}CH = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
Ta có
\(\overrightarrow {BC} .\overrightarrow {CG} = \left| {\overrightarrow {BC} } \right|.\left| {\overrightarrow {CG} } \right|.co{\rm{s}}\left( {\overrightarrow {BC} ,\overrightarrow {CG} } \right)\)
\( = BC.CG.c{\rm{os}}\left( {\overrightarrow {BC} ,\overrightarrow {CG} } \right) = BC.CG.co{\rm{s150}}^\circ \)
\( = a.\frac{{a\sqrt 3 }}{3}.\frac{{ - \sqrt 3 }}{2} = \frac{{ - {a^2}}}{2}\).
Vậy ta chọn đáp án D.
Câu 25:
 Xem đáp án
Xem đáp án
Lời giải
Gọi số cần tìm là \(\overline {abc{\rm{d}}e} \)
• Nếu a là số chẵn
Giả sử b, c là số chẵn và d, e là số lẻ
+ Chọn số cho a có 4 cách (2 ; 4 ; 6 ; 8)
+ Chọn số cho b có 3 cách
+ Chọn số cho c có 2 cách
+ Chọn số cho d có 5 cách
+ Chọn số cho e có 4 cách
Suy ra nếu a là số chẵn thì sẽ có 4 . 3 . 2 . 5 . 4 = 480 số
• Nếu a là số lẻ
Giả sử b là số lẻ và c, d, e là số chẵn
+ Chọn số cho a có 5 cách
+ Chọn số cho b có 4 cách
+ Chọn số cho c có 5 cách
+ Chọn số cho d có 4 cách
Chọn số cho e có 3 cách
Vậy khi a là số lẻ thì có 5 . 4 . 5 . 4 . 3 = 1200 (số)
Vậy có 1200 + 480 = 1680 số thỏa mãn yêu cầu đề bài.
Câu 26:
Cho hàm số y = ax – 4 . Tìm hệ số a, biết rằng
a) Đồ thị hàm số cắt đường thẳng y = 2x – 1 tại điểm có hoành độ bằng 2;
b) Đồ thị hàm số cắt đường thẳng y = –3x + 2 tại điểm có tung độ bằng 5.
 Xem đáp án
Xem đáp án
Lời giải
a) Để đường thẳng y = ax + 4 cắt đường thẳng y = 2x – 1 thì a ≠ 2.
Phương trình hoành độ giao điểm của đường thẳng y = ax + 4 và đường thẳng y = 2x – 1 là
ax – 4 = 2x – 1
⇔ ax = 2x + 3
Û (a – 2)x = 3
\( \Leftrightarrow x = \frac{3}{{a - 2}}\) (do a ≠ 2).
Do hai đường thẳng trên cắt nhau tại một điểm có hoành độ bằng 2 nên
\(\frac{3}{{a - 2}} = 2 \Leftrightarrow a - 2 = \frac{3}{2} \Leftrightarrow a = \frac{7}{2}\left( {tm} \right)\)
Vậy \[{\rm{a}} = \frac{7}{2}\].
a) Để đường thẳng y = ax + 4 cắt đường thẳng y = –3x + 2 thì a ≠ –3.
Phương trình hoành độ giao điểm của hai đường thẳng này là:
ax + 4 = –3x + 2
Û (a + 3)x = –2
\( \Leftrightarrow x = \frac{{ - 2}}{{a + 3}}\)
Thay \(x = \frac{{ - 2}}{{a + 3}}\) vào y = –3x + 2 ta được:
\[y = --3.\frac{{ - 2}}{{a + 3}} + 2 = \frac{{6 + 2a + 6}}{{a + 3}} = \frac{{2a + 12}}{{a + 3}}\]
Vậy tọa độ giao điểm của hai đường thẳng trên là \(\left( {\frac{{ - 2}}{{a + 3}};\frac{{2a + 12}}{{a + 3}}} \right)\).
Đồ thị hàm số y = ax + 4 cắt đường thẳng y = – 3x + 2 tại điểm có tung độ bằng 5 nên
\[\frac{{2a + 12}}{{a + 3}} = 5 \Rightarrow 2a + 12 = 5a + 15 \Leftrightarrow 3a = - 3 \Leftrightarrow a = - 1\left( {tm} \right)\]
Vậy a = –1.
Câu 27:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là A
Ta có:
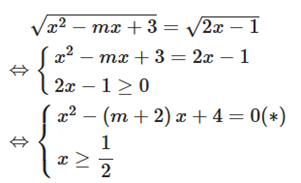
Để phương trình đã cho có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm phân biệt thỏa mãn \[{{\rm{x}}_1} > {x_2} \ge \frac{1}{2}\]
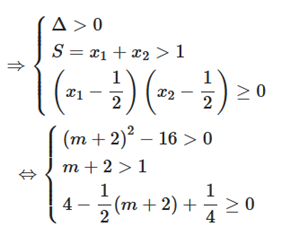
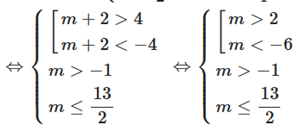
\( \Leftrightarrow 2 < m \le \frac{{13}}{2}\)
Mà m ∈ ℤ
Suy ra m ∈ {3; 4; 5; 6}.
Vậy có 4 giá trị của m thỏa mãn đề bài.
Câu 28:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \(\overrightarrow {A{\rm{E}}} = \overrightarrow {EB} + 3\overrightarrow {EC} \)
\( \Leftrightarrow \overrightarrow {EB} + 3\overrightarrow {EC} - \overrightarrow {A{\rm{E}}} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {DB} - \overrightarrow {DE} + 3\overrightarrow {DC} - 3\overrightarrow {DE} - \overrightarrow {AD} - \overrightarrow {DE} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {DB} + 3\overrightarrow {DC} - \overrightarrow {AD} - 5\overrightarrow {DE} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {DB} + 3\overrightarrow {DC} - \overrightarrow {AD} = 5\overrightarrow {DE} \)
\( \Leftrightarrow \overrightarrow {DB} + 3\overrightarrow {DC} - \overrightarrow {AD} = 5\overrightarrow {DE} \)
\( \Leftrightarrow \frac{1}{5}\overrightarrow {DB} + \frac{3}{5}\overrightarrow {DC} - \frac{1}{5}\overrightarrow {AD} = \overrightarrow {DE} \)
Vậy \(\overrightarrow {DE} = \frac{1}{5}\overrightarrow {DB} + \frac{3}{5}\overrightarrow {DC} - \frac{1}{5}\overrightarrow {AD} \).
Câu 29:
Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng song song với BD,
cắt AB ở E, cắt AD ở F.
a) Tứ giác BECD là hình gì? Vì sao?
b) Chứng minh rằng ba đường thẳng AC, BF, DE đồng quy.
 Xem đáp án
Xem đáp án
Lời giải
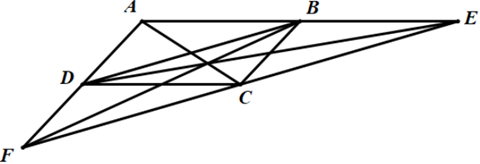
a) Vì ABCD là hình bình hành nên AB // DC, AD // BC
Hay BE // DC
Xét tứ giác BECD có
BE // DC và BD // CE
Suy ra BECD là hình bình hành.
b) Vì ABCD là hình bình hành nên AB = CD
Vì BECD là hình bình hành nên BE = CD
Suy ra AB = BE, BD = CE
Xét tứ giác BCFD có: BD // CF và BC // DF
Suy ra BCFD là hình bình hành.
Do đó DF = BC, DB = CF
Mà BC = AD (vì ABCD là hình bình hành)
Suy ra DA = DF
Ta có BD = CF, BD = CE (chứng minh trên)
Suy ra CF = CE
Xét tam giác AEF có AC, FB, ED là ba đường trung tuyến nên chúng đồng quy
Vậy ba đường thẳng AC, BF, DE đồng quy.
Câu 30:
 Xem đáp án
Xem đáp án
Lời giải
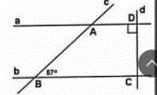
Vì d ⊥ a = {D} (giả thiết) nên \(\widehat {C{\rm{D}}A} = 90^\circ \)
Xét tứ giác ABCD có
\(\widehat {ABC} + \widehat {BC{\rm{D}}} + \widehat {C{\rm{D}}A} + \widehat {BA{\rm{D}}} = 360^\circ \)
Hay \(57^\circ + \widehat {BC{\rm{D}}} + 90^\circ + 123^\circ = 360^\circ \)
Suy ra \(\widehat {BC{\rm{D}}} = 90^\circ \)
Do đó b ⊥ d
Vậy b ⊥ d.
Câu 31:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \[{\rm{cos2x}} + 2\sqrt 3 {\mathop{\rm s}\nolimits} {\rm{inx }}.{\rm{ cosx = 2}}\]
\[ \Leftrightarrow {\rm{cos2x}} + \sqrt 3 {\mathop{\rm s}\nolimits} {\rm{in2x = 2}}\]
\[ \Leftrightarrow \frac{1}{2}{\rm{cos2x}} + \frac{{\sqrt 3 }}{2}{\mathop{\rm s}\nolimits} {\rm{in2x = 1}}\]
\[ \Leftrightarrow \sin \left( {\frac{\pi }{6} + 2{\rm{x}}} \right) = 1\]
\[ \Leftrightarrow \frac{\pi }{6} + 2{\rm{x}} = \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\]
\[ \Leftrightarrow 2{\rm{x}} = \frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\]
\[ \Leftrightarrow {\rm{x}} = \frac{\pi }{6} + k\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\]
Vậy \[{\rm{x}} = \frac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
Câu 32:
 Xem đáp án
Xem đáp án
Lời giải
Vì a + b + c = 0 nên
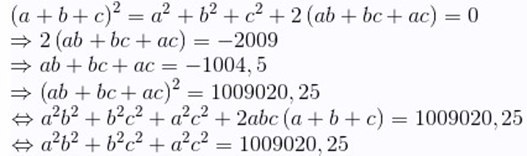
Ta có a2 + b2 + c2 = 2009
⇔ (a2 + b2 + c2)2 = 20092
⇔ a4 + b4 + c4 + 2(a2b2 + b2c2 + a2c2) = 20092
⇔ a4 + b4 + c4 + 2 . 1009020,25 = 20092
⇔ a4 + b4 + c4 = 2018040,5
Vậy A = 2018040,5.
Câu 33:
Cho tam giác ABC đều cạnh a, đường cao AH. Tính độ dài của các vecto:
\(\left| {\overrightarrow {AB} + \overrightarrow {BH} } \right|,\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|,\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).
 Xem đáp án
Xem đáp án
Lời giải
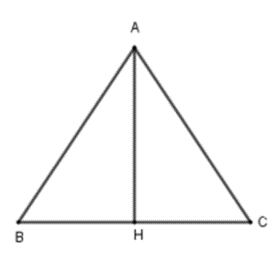
• Ta có \(\left| {\overrightarrow {AB} + \overrightarrow {BH} } \right| = \left| {\overrightarrow {AH} } \right| = AH\)
Xét tam giác ABH có \(AH = AB.\sin 60^\circ = \frac{{a\sqrt 3 }}{2}\)
Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {BH} } \right| = \frac{{a\sqrt 3 }}{2}\).
• Ta có \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = a\).
• Vì tam giác ABC đều có AH là đường cao nên AH là đường trung tuyến
Suy ra H là trung điểm của BC
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AH} } \right| = 2AH = 2.\frac{{a\sqrt 3 }}{2} = a\sqrt 3 \).
Câu 34:
 Xem đáp án
Xem đáp án
Lời giải
+) Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.
+) Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai đáy của hình thang cân.
Câu 35:
Chứng minh
a) \(1 + {\tan ^2}\alpha = \frac{1}{{{\rm{co}}{{\rm{s}}^2}\alpha }}\).
b) \(1 + {\cot ^2}\alpha = \frac{1}{{{\rm{si}}{{\rm{n}}^2}\alpha }}\).
 Xem đáp án
Xem đáp án
Lời giải
a) Ta có \(1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{\rm{co}}{{\rm{s}}^2}\alpha }} = \frac{{co{{\rm{s}}^2}\alpha + {{\sin }^2}\alpha }}{{{\rm{co}}{{\rm{s}}^2}\alpha }} = \frac{1}{{{\rm{co}}{{\rm{s}}^2}\alpha }}\).
Vậy \(1 + {\tan ^2}\alpha = \frac{1}{{{\rm{co}}{{\rm{s}}^2}\alpha }}\).
b) Ta có \(1 + {\cot ^2}\alpha = 1 + \frac{{{\rm{co}}{{\rm{s}}^2}\alpha }}{{{\rm{si}}{{\rm{n}}^2}\alpha }} = \frac{{{\rm{si}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{s}}^2}\alpha }}{{{\rm{si}}{{\rm{n}}^2}\alpha }} = \frac{1}{{{\rm{si}}{{\rm{n}}^2}\alpha }}\).
Vậy \(1 + {\cot ^2}\alpha = \frac{1}{{{\rm{si}}{{\rm{n}}^2}\alpha }}\).
Câu 36:
Đổi đơn vị thời gian:
a) \(\frac{9}{5}\) giờ = ... giờ ... phút.
b) 1,25 giờ = ... giờ ... phút.
 Xem đáp án
Xem đáp án
Lời giải
Vì 1 giờ = 60 phút nên
a) \(\frac{9}{5}\) giờ = 1 giờ 48 phút.
b) 1,25 giờ = 0 giờ 75 phút = 75 phút.
Câu 37:
Tìm số tự nhiên n, để
a) n + 4 ⋮ n.
b) 5n – 6 ⋮ n (n < 1).
c) 143 – 12n ⋮ n (với n < 12).
 Xem đáp án
Xem đáp án
Lời giải
a) Để n + 4 ⋮ n ⇔ 4 ⋮ n
⇔ n ∈ Ư(4) = {–4; –2; –1; 1; 2 ; 4}
Vậy n ∈ {–4; –2; –1; 1; 2 ; 4}.
b) 5n – 6 ⋮ n (n < 1)
⇔ 6 ⋮ n (vì 5n ⋮ n)
⇔ n ∈ Ư(6) = {–6; –3; –2; –1; 1; 2 ; 3; 6}
Mà n < 1 nên n ∈ {–6; –3; –2; –1}
Vậy n ∈ {–6; –3; –2; –1}.
c) 143 – 12n ⋮ n (với n < 12).
⇔ 143 ⋮ n (vì 12n ⋮ n)
⇔ n ∈ Ư(143) = {–143; – 13; – 11; – 1; 1; 11 ; 13; 143}
Mà n < 12 nên n ∈ {– 143; – 13; – 11; – 1; 1; 11}
Vậy n ∈ {– 143; – 13; – 11; – 1; 1; 11}.
Câu 38:

 Xem đáp án
Xem đáp án
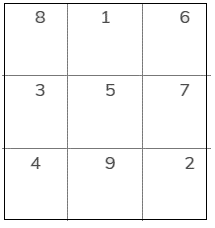
Lời giải
Ta điền như bảng sau để được tổng của 3 ô hàng dọc, hàng ngang và đường chéo đều bằng nhau và bằng 15
Câu 39:
 Xem đáp án
Xem đáp án
Lời giải
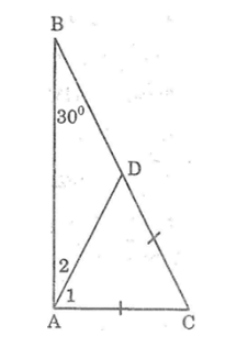
Xét ΔABC, ta có: \(\widehat A = 90^\circ ,\widehat B = 30^\circ \)
Suy ra \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 90^\circ - 30^\circ = 60^\circ \)
Trên cạnh BC lấy điểm D sao cho CD = AC
Suy ra ΔACD cân tại C
Mà \(\widehat C = 60^\circ \), suy ra ΔACD đều
Do đó AC = AD = DC và \({\widehat A_1} = 60^\circ \)
Ta có \({\widehat A_1} + {\widehat A_2} = \widehat {BAC} = 90^\circ \)
Suy ra \({\widehat A_2} = 90 - {\widehat A_1} = 90^\circ - 60^\circ = 30^\circ \)
Xét tam giác ABD có \({\widehat A_2} = \widehat B\left( { = 30^\circ } \right)\)
Suy ra ΔADB cân tại D nên AD = DB
Suy ra AC = CD = DB mà CD + DB = BC
Do đó \(AC = \frac{1}{2}BC\)
Vậy \(AC = \frac{1}{2}BC\).
Câu 40:
Tìm x biết
a) \(\sqrt {{{\left( {x - 3} \right)}^2}} = 9\).
b) \(\sqrt {4{{\rm{x}}^2} + 4{\rm{x}} + 1} = 6\).
 Xem đáp án
Xem đáp án
Lời giải
a) \(\sqrt {{{\left( {x - 3} \right)}^2}} = 9\)
\( \Leftrightarrow \left| {x - 3} \right| = 9\)
\( \Leftrightarrow \left[ \begin{array}{l}x - 3 = 9\\x - 3 = - 9\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 12\\x = - 6\end{array} \right.\)
Vậy x ∈ {12; – 6}.
b) \(\sqrt {4{{\rm{x}}^2} + 4{\rm{x}} + 1} = 6\)
\( \Leftrightarrow \sqrt {{{\left( {2{\rm{x}} + 1} \right)}^2}} = 6\)
\( \Leftrightarrow \left| {2x + 1} \right| = 6\)
\( \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 6\\2x + 1 = - 6\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}2x = 5\\2x = - 7\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{5}{2}\\x = \frac{{ - 7}}{2}\end{array} \right.\)
Vậy \[{\rm{x}} \in \left\{ {\frac{5}{2};\frac{{ - 7}}{2}} \right\}\].
Câu 41:
 Xem đáp án
Xem đáp án
Lời giải
Vì a chia 19 dư 3 nên a = 19m + 3
Vì b chia 38 dư 5 nên b = 38n + 5
Ta có:
3a + 2b
= 3(19m + 3) + 2(38n + 5)
= 57m + 9 + 76n + 10
= 57m + 76n + 19
Vì 57m ⋮ 19; 76n ⋮ 19 và 19 ⋮ 19
Suy ra (57m + 76n + 19) ⋮ 19
Vậy 3a + 2b ⋮ 19.
Câu 42:
 Xem đáp án
Xem đáp án
Lời giải
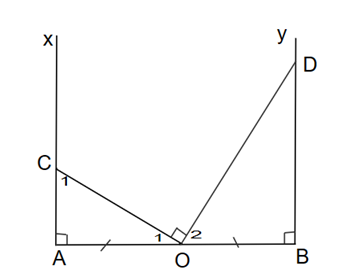
Vì tam giác OAC vuông tại A nên \(\widehat {{C_1}} + \widehat {{O_1}} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Ta có \(\widehat {{O_2}} + \widehat {{O_1}} + \widehat {CO{\rm{D}}} = 180^\circ \)
Mà \(\widehat {CO{\rm{D}}} = 90^\circ \)
Suy ra \(\widehat {{O_2}} + \widehat {{O_1}} = 90^\circ \)
Lại có \(\widehat {{C_1}} + \widehat {{O_1}} = 90^\circ \) 9 (chứng minh trên)
Suy ra \(\widehat {{O_2}} = \widehat {{C_1}}\)
Xét △AOC và △BDO có
\(\widehat {{O_2}} = \widehat {{C_1}}\) (chứng minh trên)
\(\widehat {OAC} = \widehat {OB{\rm{D}}}\left( { = 90^\circ } \right)\)
Suy ra (g.g)
Do đó \(\frac{{AO}}{{B{\rm{D}}}} = \frac{{AC}}{{BO}}\)
Lại có \(AO = BO = \frac{1}{2}AB\)
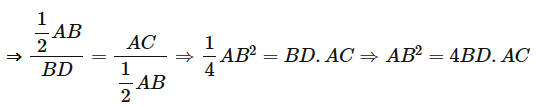
Vậy AB2 = 4AC . BD
Câu 43:
Cho tam giác ABC nhọn có \(\widehat A = 70^\circ \) và điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB. Gọi F là điểm đối xứng với D qua AC. Đường thẳng EF cách AB, AC theo thứ tự tại M, N.
a) Tính các góc của tam giác AEF.
b) Chứng minh rằng DA là tia phân giác của góc MDN.
 Xem đáp án
Xem đáp án
Lời giải
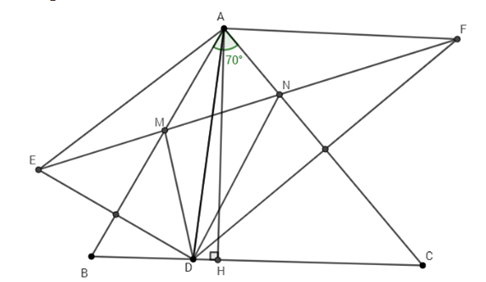
a) Vì E đối xứng D qua AB nên AB là trung trực của DE
Suy ra AE = AD
Do đó tam giác AED cân tại A
Mà AB là đường trung trực
Suy ra AB là phân giác của \(\widehat {DA{\rm{E}}}\)
Do đó \(\widehat {DAB} = \widehat {BA{\rm{E}}} = \frac{1}{2}\widehat {DA{\rm{E}}}\)
Vì F đối xứng D qua AC nên AC là trung trực của DF
Suy ra AF = AD
Do đó tam giác AFD cân tại A
Mà AC là đường trung trực
Suy ra AC là phân giác của \(\widehat {DAF}\)
Do đó \(\widehat {DAC} = \widehat {CAF} = \frac{1}{2}\widehat {DAF}\)
Ta có \(\widehat {F{\rm{AE}}} = \widehat {F{\rm{AD}}} + \widehat {DAE} = 2\widehat {CA{\rm{D}}} + 2\widehat {BAD} = 2\widehat {BAC} = 2.70^\circ = 140^\circ \)
Ta có AF = AE (= AD)
Suy ra tam giác AFE cân tại A, do đó \[\widehat {{\rm{AFE}}} = \widehat {{\rm{AEF}}}\]
Xét tam giác AEF có
\[\widehat {{\rm{AFE}}} + \widehat {{\rm{AEF}}} + \widehat {F{\rm{AE}}} = 180^\circ \] (tổng ba góc trong một tam giác)
Mà \[\widehat {{\rm{AFE}}} = \widehat {{\rm{AEF}}},\widehat {FA{\rm{E}}} = 140^\circ \] (chứng minh trên)
Suy ra \[\widehat {{\rm{AFE}}} = \widehat {{\rm{AEF}}} = \frac{{180^\circ - 140^\circ }}{2} = 20^\circ \]
b) Xét DAME và DAMD có
AM là cạnh chung;
\(\widehat {E{\rm{A}}M} = \widehat {DAM}\)(chứng minh trên);
AD = AE (chứng minh trên)
Do đó DAME = DAMD (c.g.c)
Suy ra \(\widehat {{\rm{AE}}M} = \widehat {ADM}\) (hai góc tương ứng)
Xét DANF và DAND có
AN là cạnh chung;
\(\widehat {{\rm{FAN}}} = \widehat {DAN}\)(chứng minh trên);
AD = AF (chứng minh trên)
Do đó DANF = DAND (c.g.c)
Suy ra \(\widehat {{\rm{AFN}}} = \widehat {ADN}\) (hai góc tương ứng)
Mà \(\widehat {{\rm{AE}}M} = \widehat {ADM}\), \[\widehat {{\rm{AFE}}} = \widehat {{\rm{AEF}}}\]
Suy ra \(\widehat {{\rm{ADM}}} = \widehat {ADN}\)
Do đó DA là tia phân giác của góc MDN.
c) Gọi giao điểm của DE và AB là P, giao điểm của DF và AC là Q
Khi đó P là trung điểm của DE, Q là trung điểm của DF
Xét tam giác DFE có P, Q lần lượt là trung điểm của DE, DF
Suy ra PQ là đường trung bình
Do đó PQ // FE và \(PQ = \frac{1}{2}F{\rm{E}}\)
Vì M thuộc trung trực của DE nên MD = ME
Vì N thuộc trung trực của DF nên ND = NF
Chu vì tam giác DMN là
DM + DN + MN = ME + NF + MN = FE
Để chu vi tam giác DMN nhỏ nhất
⇔ FE nhỏ nhất
⇔ PQ nhỏ nhất (vì \(PQ = \frac{1}{2}F{\rm{E}}\))
⇔ PQ // BC và \(PQ = \frac{1}{2}BC\)
⇔ PQ là đường trung bình của tam giác ABC
⇔ D là trung điểm của BC
Vậy D là trung điểm của BC thì chu vi tam giác DMN nhỏ nhất.
Câu 44:
Cho tam giác abc vuông tại A, M là trung điểm của BC, D, E lần lượt là hình chiếu của M trên AB và AC.
a) Tứ giác ADME là hình gì, tại sao?
b) Chứng minh \(DE = \frac{1}{2}BC\)
c) Gọi P là trung điểm của BM, Q là trung điểm của MC, chứng minh tứ giác DPQE là hình bình hành.
Từ đó chứng minh: tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.
d) Tam giác vuông ABC ban đầu cần thêm điều kiện gì để hình bình hành DPQE là hình chữ nhật?
 Xem đáp án
Xem đáp án
Lời giải
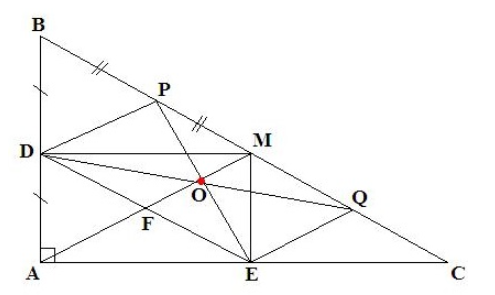
a) Ta có D, E là hình chiếu của M trên AB, AC
Nên DM ⊥ AB và ME ⊥ AC, hay \(\widehat {A{\rm{D}}M} = \widehat {A{\rm{E}}M} = 90^\circ \)
Xét tứ giác ADME có \(\widehat {DA{\rm{E}}} = \widehat {A{\rm{D}}M} = \widehat {A{\rm{E}}M} = 90^\circ \)
Suy ra ADME là hình chữ nhật.
b) Xét ΔABC vuông tại A có M là trung điểm BC
Suy ra \(AM = \frac{1}{2}BC\)
Vì ADME là hình chữ nhật có AM, DE là hai đường chéo, suy ra AM = DE
Mà \(AM = \frac{1}{2}BC\)
Do đó \(DE = \frac{1}{2}BC\).
c) Ta có AD ⊥ AC và ME ⊥ AC, suy ra AD // ME
Mà M là trung điểm của BC
Suy ra E là trung điểm của AC
Xét tam giác AMC có E, Q lần lượt là trung điểm của AC, MC
Suy ra QE là đường trung bình
Do đó QE // AM, \(QE = \frac{1}{2}AM\) (1)
Ta có DM ⊥ AB và AB ⊥ AC
Suy ra DM // AC
Mà M là trung điểm của BC
Suy ra D là trung điểm của AB
Xét ΔBAM có D, P lần lượt là trung điểm của AB và BM
Suy ra DP là đường trung bình của ΔBAM
Do đó DP // AM và \(DP = \frac{1}{2}AM\) (2)
Từ (1) và (2) suy ra DP // EQ, DP = EQ
Do đó DPQE là hình bình hành.
Gọi O là tâm đối xứng của DPQE (là giao điểm 2 đường chéo)
Ta có P, Q lần lượt là trung điểm của BM, MC và M là trung điểm BC
Suy ra M là trung điểm PQ
Xét hình bình hành DPQE có AM // DP và M là trung điểm PQ
Suy ra AM là đường trung bình của DPQE
Do đó AM đi qua trung điểm DE, gọi điểm đó là F
Từ đó AM là trục đối xứng của DPQE tức là đi qua O
Vậy tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.
d) Để hình bình hành DPQE là hình chữ nhật thì \(\widehat {APQ} = \widehat {PQE} = \widehat {QE{\rm{D}}} = \widehat {E{\rm{D}}P} = 90^\circ \)
Ta xét ΔBAM nếu DP ⊥ BM thì AM ⊥ BM
Xét ΔABC có AM vừa là đường trung tuyến vừa là đường cao
Suy ra ΔABC vuông cân tại A
Vậy để hình bình hành DPQE là hình chữ nhật thì tam giác vuông ΔABC cần thêm điều kiện cân tại A.
Câu 45:
Cho tam giác ABC điểm M nằm trong tam giác. Gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Gọi A’, B’, C’ thứ tự là điểm đối xứng của M qua D, E, F
a) Chứng minh tứ giác AB’A’B là hình bình hành.
b) Gọi O là giao điểm của AA’ và BB’, chứng minh C và C’ đối xứng nhau qua điểm O.
 Xem đáp án
Xem đáp án
Lời giải
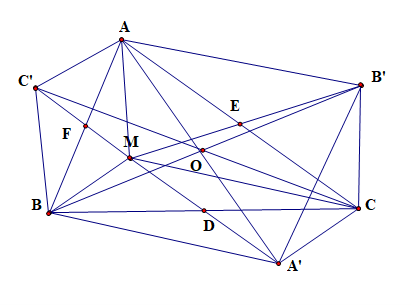
a) Xét tứ giác AB’CM có
AC cắt MB' tại trung điểm E của mỗi đường và AC, MB’ là hai đường chéo
Suy ra AB'CM là hình bình hành
Do đó AB' // MC, AB' = MC
Xét tứ giác BMCA’ có
BC cắt MA' tại trung điểm D của mỗi đường và BC, MA’ là hai đường chéo
Suy ra BMCA' là hình bình hành
Do đó MC // A'B, MC = A'B.
Ta có AB' // MC, MC // A'B (chứng minh trên), suy ra AB’ // A’B.
Ta có MC = A'B, AB' = MC (chứng minh trên), suy ra AB’ = A’B.
Xét tứ giác AB’A’B có AB’ // A’B và AB’ = A’B
Suy ra tứ giác AB'A'B là hình bình hành.
b) Xét hình bình hành AB'A'B có AA’ và BB’ cắt nhau tại O
Suy ra O là trung điểm của AA’.
Chứng minh tương tự câu a ta có: AC’ = A’C (= BM) và AC’ // A’C (// BM)
Suy ra AC’A’C là hình bình hành.
Mà O là trung điểm của AA’
Suy ra O là trung điểm của CC’.
Hay C và C’ đối xứng nhau qua điểm O
Vậy C và C’ đối xứng nhau qua điểm O.
Câu 46:
Cho điểm A nằm ngoài đường tròn (O; R). Từ A vẽ các tiếp tuyến AB, AC và cát tuyến ADE đến đường tròn (O). Gọi H là trung điểm của DE.
a) Chứng minh 5 điểm A, B, H, O, C cùng nằm trên một đường tròn.
b) Chứng minh HA là tia phân giác của góc BHC.
 Xem đáp án
Xem đáp án
Lời giải
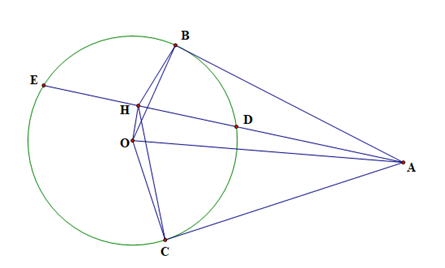
a) Vì AC là tiếp tuyến của (O) nên AC ⊥ OC, hay tam giác OAC vuông tại C
Suy ra C thuộc đường tròn đường kính AO (1)
Xét (O) có DE là dây cung, H là trung điểm của DE, suy ra DE ⊥ OH
Hay tam giác OHA vuông tại H
Suy ra H thuộc đường tròn đường kính AO (2)
Vì AB là tiếp tuyến của (O) nên AB ⊥ OB, hay tam giác OAB vuông tại B
Suy ra B thuộc đường tròn đường kính AO (3)
Từ (1), (2) và (3) suy ra 3 điểm C, H, B cùng nằm trên đường tròn đường kính AO.
Vậy 5 điểm A, B, H, O, C cùng nằm trên đường tròn đường kính AO.
b) • Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A
Suy ra \(\widehat {AOB} = \widehat {AOC}\) (4)
• Xét đường tròn đường kính AO có
\(\widehat {AOB},\widehat {AHB}\) là hai góc nội tiếp cùng chắn cung AB
Suy ra \(\widehat {AOB} = \widehat {AHB}\) (5)
• Xét đường tròn đường kính AO có
\(\widehat {AOC},\widehat {AHC}\) là hai góc nội tiếp cùng chắn cung AC
Suy ra \(\widehat {AOC} = \widehat {AHC}\) (6)
Từ (4), (5) và (6) suy ra \(\widehat {AHB} = \widehat {AHC}\).
Suy ra HA là tia phân giác của góc BHC
Vậy HA là tia phân giác của góc BHC.
Câu 47:
 Xem đáp án
Xem đáp án
Lời giải
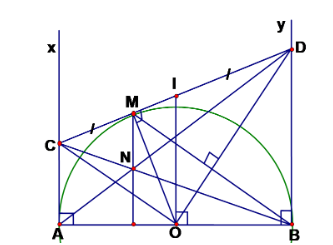
Gọi I là trung điểm của CD ta có I là tâm đường tròn ngoại tiếp tam giác COD đường kính CD
Xét (O) có CM, CA là hai tiếp tuyến cắt nhau tại C
Suy ra \(\widehat {AOC} = \widehat {MOC} = \frac{1}{2}\widehat {AOM}\)
Xét (O) có DM, DB là hai tiếp tuyến cắt nhau tại D
Suy ra \(\widehat {BOD} = \widehat {MOD} = \frac{1}{2}\widehat {BOM}\)
Ta có \(\widehat {AOM} + \widehat {BOM} = 180^\circ \) (hai góc kề bù)
\( \Leftrightarrow \frac{1}{2}\widehat {AOM} + \frac{1}{2}\widehat {BOM} = 90^\circ \)
\( \Leftrightarrow \widehat {COM} + \widehat {DOM} = 90^\circ \)
\( \Leftrightarrow \widehat {COD} = 90^\circ \)
Hay tam giác COD vuông tại O
Nên IO là bán kính của (I)
Ta có AB ⊥ CA, AB ⊥ BD
Suy ra AC // BD (quan hệ từ vuông góc đến song song)
Do đó ACDB là hình thang
Mà I là trung điểm của CD; O là trung điểm của AB
Suy ra IO là đường trung bình của hình thang ACDB
Do đó IO // AC
Mà AB ⊥ CA
Nên AB ⊥ OI (quan hệ từ vuông góc đến song song)
Xét (I) có OI là bán kính, AB ⊥ OI (chứng minh trên)
Suy ra AB là tiếp tuyến tại O của đường tròn đường kính CD
Vậy AB là tiếp tuyến của đường tròn đường kính CD.
