 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Đáp án đúng là: D
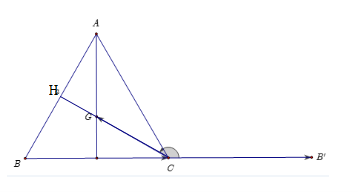
Vì tam giác ABC đều cạnh a nên AB = BC = AC = a và \(\widehat {ACB} = 60^\circ \)
Vì tam giác ABC đều có G là trọng tâm nên G là giao điểm của ba đường phân giác
Suy ra CG là tia phân giác của \(\widehat {ACB}\)
Do đó \(\widehat {BCG} = \frac{1}{2}\widehat {ACB} = \frac{1}{2}.60^\circ = 30^\circ \)
Gọi CB’ là tia đối của tia BC
Góc tạo bởi \(\overrightarrow {BC} ,\overrightarrow {CG} \) là \(\widehat {B'CG}\)
Ta có \(\widehat {B'CG} + \widehat {BCG} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {B'CG} = 180^\circ - 30^\circ = 150^\circ \)
Gọi H là giao điểm của CG và AB
Khi đó CH ⊥ AB và H là trung điểm của AB
Hay tam giác ACH vuông tại H
Suy ra \(CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
Do đó \(CG = \frac{2}{3}CH = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
Ta có
\(\overrightarrow {BC} .\overrightarrow {CG} = \left| {\overrightarrow {BC} } \right|.\left| {\overrightarrow {CG} } \right|.co{\rm{s}}\left( {\overrightarrow {BC} ,\overrightarrow {CG} } \right)\)
\( = BC.CG.c{\rm{os}}\left( {\overrightarrow {BC} ,\overrightarrow {CG} } \right) = BC.CG.co{\rm{s150}}^\circ \)
\( = a.\frac{{a\sqrt 3 }}{3}.\frac{{ - \sqrt 3 }}{2} = \frac{{ - {a^2}}}{2}\).
Vậy ta chọn đáp án D.
Cho tam giác abc vuông tại A, M là trung điểm của BC, D, E lần lượt là hình chiếu của M trên AB và AC.
a) Tứ giác ADME là hình gì, tại sao?
b) Chứng minh \(DE = \frac{1}{2}BC\)
c) Gọi P là trung điểm của BM, Q là trung điểm của MC, chứng minh tứ giác DPQE là hình bình hành.
Từ đó chứng minh: tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.
d) Tam giác vuông ABC ban đầu cần thêm điều kiện gì để hình bình hành DPQE là hình chữ nhật?
Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm.
a) Tính số đo góc B, góc C (làm tròn đến độ) và đường cao AH.
b) Chứng minh rằng AB. cos B + AC . cosC = BC.
c) Trên cạnh AC lấy điểm D sao cho DC = 2DA. Vẽ DE vuông góc với BC tại E. Chứng minh rằng \(\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{4}{{9D{E^2}}}\).
Cho điểm A nằm ngoài đường tròn (O; R). Từ A vẽ các tiếp tuyến AB, AC và cát tuyến ADE đến đường tròn (O). Gọi H là trung điểm của DE.
a) Chứng minh 5 điểm A, B, H, O, C cùng nằm trên một đường tròn.
b) Chứng minh HA là tia phân giác của góc BHC.
Cho tam giác ABC đều cạnh a, đường cao AH. Tính độ dài của các vecto:
\(\left| {\overrightarrow {AB} + \overrightarrow {BH} } \right|,\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|,\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).
Cho tam giác ABC đều cạnh a, tâm O. Hãy tính:
a) \(\overrightarrow {AB} .\overrightarrow {AC} \).
b) \(\overrightarrow {AB} .\overrightarrow {BC} \).
c) \(\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right)\).
d) \(\left( {\overrightarrow {AB} + 2\overrightarrow {AC} } \right)\left( {\overrightarrow {AB} - 3\overrightarrow {BC} } \right)\).
Cho tam giác ABC điểm M nằm trong tam giác. Gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Gọi A’, B’, C’ thứ tự là điểm đối xứng của M qua D, E, F
a) Chứng minh tứ giác AB’A’B là hình bình hành.
b) Gọi O là giao điểm của AA’ và BB’, chứng minh C và C’ đối xứng nhau qua điểm O.
Cho hàm số y = ax – 4 . Tìm hệ số a, biết rằng
a) Đồ thị hàm số cắt đường thẳng y = 2x – 1 tại điểm có hoành độ bằng 2;
b) Đồ thị hàm số cắt đường thẳng y = –3x + 2 tại điểm có tung độ bằng 5.