- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 39)
-
12932 lượt thi
-
47 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Lời giải
Điều kiện xác định x ≥ 0, x ≠ 1
Vì P2 > P
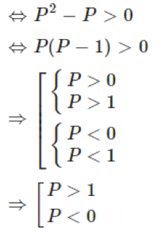
+) Với P > 1
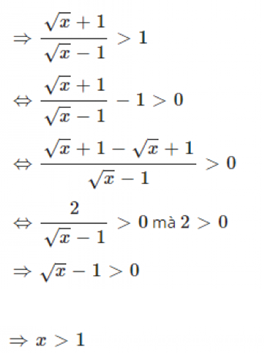
+) Với P < 0
Suy ra \(\frac{{\sqrt x + 1}}{{\sqrt x - 1}} < 0\)
Mà \(\sqrt x + 1 > 0\)
Suy ra \(\sqrt x - 1 < 0\)
Hay \(\sqrt x < 1\)
Mà x ≥ 0, x ≠ 1
Suy ra 0 ≤ x < 1
Vậy để P2 > P thì 0 ≤ x < 1 hoặc x > 1.
Câu 2:
Cho biểu thức:
\(A = \frac{{\sqrt x + 1}}{{\sqrt x - 2}} + \frac{2}{{\sqrt x + 3}} - \frac{{9\sqrt x - 3}}{{x + \sqrt x - 6}}\) và \(B = \frac{{x - \sqrt x + 1}}{{\sqrt x - 1}}\) với x ≥ 0, x ≠ 1, x ≠ 4.
a) Tính giá trị biểu thức B khi x = 9.
b) Rút gọn A.
c) Chứng minh rằng khi A > 0 thì B ≥ 3.
 Xem đáp án
Xem đáp án
Lời giải
a) Thay x = 9 (thỏa mãn) vào B ta có
\(B = \frac{{x - \sqrt x + 1}}{{\sqrt x - 1}} = \frac{{9 - \sqrt 9 + 1}}{{\sqrt 9 - 1}} = \frac{{9 - 3 + 1}}{{3 - 1}} = \frac{7}{2}\).
b) Với x ≥ 0, x ≠ 1, x ≠ 4, ta có
\(A = \frac{{\sqrt x + 1}}{{\sqrt x - 2}} + \frac{2}{{\sqrt x + 3}} - \frac{{9\sqrt x - 3}}{{x + \sqrt x - 6}}\)
\(A = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 3} \right) + 2\left( {\sqrt x - 2} \right) - 9\sqrt x + 3}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 3} \right)}}\)
\(A = \frac{{x + 4\sqrt x + 3 + 2\sqrt x - 4 - 9\sqrt x + 3}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 3} \right)}}\)
\(A = \frac{{x - 3\sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 3} \right)}}\)
\(A = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 3} \right)}} = \frac{{\sqrt x - 1}}{{\sqrt x + 3}}\).
c) Với x ≥ 0, x ≠ 1, x ≠ 4, ta có:
A > 0 \[ \Leftrightarrow \frac{{\sqrt x - 1}}{{\sqrt x + 3}} > 0\]
\( \Leftrightarrow \sqrt x - 1 > 0\) (vì \(\sqrt x + 3 > 0\))
\( \Leftrightarrow \sqrt x > 1\)
⇔ x > 1
Ta có \(B = \frac{{x - \sqrt x + 1}}{{\sqrt x - 1}} = \frac{{\sqrt x \left( {\sqrt x - 1} \right) + 1}}{{\sqrt x - 1}} = \sqrt x + \frac{1}{{\sqrt x - 1}}\)
Do \(\sqrt x > 1\) nên \(\sqrt x - 1 > 0\)
Áp dụng bất đẳng thức Cô – si ta có
\(B = \sqrt x - 1 + \frac{1}{{\sqrt x - 1}} + 1 \ge 2\sqrt {\left( {\sqrt x - 1} \right).\frac{1}{{\sqrt x - 1}}} + 1 = 2 + 1 = 3\)
Dấu “ = ” xảy ra khi \(\sqrt x - 1 = \frac{1}{{\sqrt x - 1}}\)
\( \Leftrightarrow {\left( {\sqrt x - 1} \right)^2} = 1 \Leftrightarrow \sqrt x - 1 = 1\) (do \(\sqrt x - 1 > 0\))
Û x = 4 (thỏa mãn).
Vậy khi A > 0 thì B ≥ 3.
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải
Gọi số cần lập là \(\overline {abcde} \) (0 ≤ a, b, c, d, e ≤ 9; a ≠ 0; a, b, c, d, e ∈ ℕ)
+) Nếu a = 6, b = 5
Chọn tùy ý các chữ số c, d, e trong 9 chữ số đã cho ta luôn được số thỏa mãn trừ trường hợp c = d = e = 0.
Số số lập được là: 93 – 1 = 728 số
+) Nếu a = 6, b ∈ {6; 8; 9}
Chọn tùy ý các chữ số c, d, e trong 9 chữ số đã cho ta luôn được số thỏa mãn
Số số lập được là: 3 . 93 = 2 187 số
+) Nếu a ∈ {8; 9}
Chọn tùy ý các chữ số b, c, d, e trong 9 chữ số đã cho ta luôn được số thỏa mãn
Số số lập được là: 2 . 94 = 13 122 số
Vậy số các số lập được thỏa mãn đề bài là 728 + 2 187 + 13 122 = 16 037 số.
Câu 4:
 Xem đáp án
Xem đáp án
Lời giải
Vì là số lẻ nên chữ số cuối cùng là số 7
Vì số đứng đầu phải khác 0 nên ta có 4 cách chọn
Có 4 cách chọn cho số thứ 2 và 3 cách chọn chỗ số thứ 3
Vậy có 4 × 4 × 3 = 48 số có thể tạo ra thỏa mãn yêu cầu đề bài.
Câu 5:
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
\[cos7x.cos5x--\sqrt 3 sin2x = 1--sin7x.sin5x\]
\[ \Leftrightarrow cos7x.cos5x + sin7x.sin5x--\sqrt 3 sin2x = 1\]
\[ \Leftrightarrow cos\left( {7x - 5x} \right)--\sqrt 3 sin2x = 1\]
\[ \Leftrightarrow cos2x--\sqrt 3 sin2x = 1\]
\( \Leftrightarrow \frac{1}{2}co{\rm{s2x}} - \frac{{\sqrt 3 }}{2}\sin 2{\rm{x = }}\frac{1}{2}\)
\[ \Leftrightarrow {\rm{cos}}\frac{\pi }{3}cos2{\rm{x}} - \sin \frac{\pi }{3}\sin 2{\rm{x}} = \frac{1}{2}\]
\[ \Leftrightarrow {\rm{cos}}\left( {\frac{\pi }{3} + 2{\rm{x}}} \right) = \frac{1}{2}\]
\( \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{3} + 2{\rm{x}} = \frac{\pi }{3} + k2\pi \\\frac{\pi }{3} + 2{\rm{x}} = - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}{\rm{x}} = k\pi \\{\rm{x}} = - \frac{\pi }{3} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vậy phương trình có nghiệm là: \[{\rm{x}} = k\pi ;{\rm{x}} = - \frac{\pi }{3} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
Câu 6:
Một khu rừng hình chữ nhật có chu vi 5km 60dam. Chiều dài hơn chiều rộng 800m
a) Hỏi diện tích khu rừng đó bằng bao nhiêu ha ? Bao nhiêu m2?
b) Biết \(\frac{1}{3}\) diện tích khu rừng trồng cây mới. Tính tỉ số diện tích trồng cây mới và phần diện tích còn lại của khu rừng.
 Xem đáp án
Xem đáp án
Lời giải
Đổi 5km 60dam = 5 600 m
a) Nửa chu vi khu rừng đó là:
5600 : 2 = 2 800 (m)
Chiều rộng khu rừng đó là:
(2800 – 800) : 2 = 1000 (m)
Chiều dài khu rừng đó là: 1000 + 800 = 1 800 (m)
Diện tích khu rừng đó là : 1 800 × 1000 = 1 800 000 (m2) = 180 ha
b) Diện tích phần còn lại của khu rừng chiếm : \(1 - \frac{1}{3} = \frac{2}{3}\) (diện tích khu rừng)
Tỉ số diện tích trồng cây mới và diện tích còn lại của khu rừng là: \(\frac{1}{3}:\frac{2}{3} = \frac{1}{2}\)
Vậy tỉ số diện tích trồng cây mới và phần diện tích còn lại của khu rừng là \(\frac{1}{2}\).
Câu 7:
 Xem đáp án
Xem đáp án
Lời giải
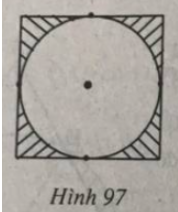
Gọi R là bán kính hình tròn
Suy ra cạnh hình vuông là 2R
Diện tích hình vuông là: Shv = 4R2
Diện tích hình tròn là: Stròn = πR2
Theo đề, ta có Ssọc = 86
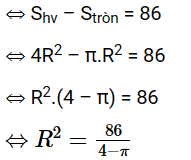
Suy ra \(R = \sqrt {\frac{{86}}{{4 - \pi }}} \)
Vậy diện tích hình tròn là \(\pi .\frac{{86}}{{4 - \pi }} \approx 314,74\) cm2.
Câu 8:
 Xem đáp án
Xem đáp án
Lời giải
Áp dụng quy tắc trung điểm ta có
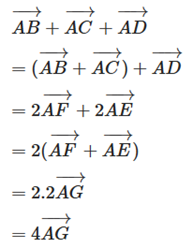
Vậy \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{\rm{D}}} = 4\overrightarrow {AG} \).
Câu 9:
Tìm x biết:
a) x5 + x4 + x + 1 = 0;
b) x4 + 3x3 – x – 3 = 0;
c) x3 – 5x2 – x + 5 = 0;
d) x(x – 5) – 4x + 20 = 0.
 Xem đáp án
Xem đáp án
Lời giải
a) x5 + x4 + x + 1 = 0
⇔ x4(x + 1) + (x + 1) = 0
⇔ (x + 1)(x4 + 1) = 0
⇔ x + 1 = 0 (vì x4 + 1 > 0)
⇔ x = – 1
Vậy x = – 1.
b) x4 + 3x3 – x – 3 = 0
⇔ x3(x + 3) – (x + 1) = 0
⇔ (x + 3)(x3 – 1) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\{x^3} - 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 1\end{array} \right.\)
Vậy x ∈ {– 3; 1}.
c) x3 – 5x2 – x + 5 = 0
⇔ x(x2 – 1) – 5(x2 – 1) = 0
⇔ (x2 – 1)(x – 5) = 0
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} - 1 = 0\\x - 5 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 5\end{array} \right.\)
Vậy x ∈ {1; 5; – 1}.
d) x(x – 5) – 4x + 20 = 0
⇔ x(x – 5) – 4(x – 5)= 0
⇔ (x – 4)(x – 5) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x - 4 = 0\\x - 5 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 5\end{array} \right.\)
Vậy x ∈ {4; 5}.
Câu 10:
Cho hàm số bậc nhất y = (m – 1)x + 2m – 5 (d1).
a) Tính giá trị của m để đường thẳng (d1) song song với đường thẳng y = 3x + 1 (d2).
b) Với giá trị nào của m thì đường thẳng (d1) và (d2) cắt nhau tại một điểm trên trục hoành.
 Xem đáp án
Xem đáp án
Lời giải
Hàm số y = (m – 1)x + 2m – 5 là hàm số bậc nhất khi m – 1 ≠ 0 Û m ≠ 1
a) Đường thẳng (d1) song song với đường thẳng y = 3x + 1 (d2)
\( \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 3\\2m - 5 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 4\\m \ne 3\end{array} \right. \Leftrightarrow m = 4\).
Vậy m = 4 thỏa mãn yêu cầu đề bài.
b) Để (d1) và (d2) cắt nhau thì \(m - 1 \ne 3 \Leftrightarrow m \ne 4\).
Phương trình hoành độ giao điểm của (d1) và (d2) là:
(m – 1)x + 2m – 5 = 3x + 1
Û (m – 4)x = 6 – 2m
\( \Leftrightarrow x = \frac{{6 - 2m}}{{m - 4}}\) (do \(m \ne 4\)).
Thay \[x = \frac{{6 - 2m}}{{m - 4}}\] vào phương trình đường thẳng (d2): y = 3x + 1 ta được:
\[y = 3.\frac{{6 - 2m}}{{m - 4}} + 1 = \frac{{18 - 6m + m - 4}}{{m - 4}} = \frac{{14 - 5m}}{{m - 4}}\]
Do đó tọa độ giao điểm của (d1) và (d2) là \[\left( {\frac{{6 - 2m}}{{m - 4}};\frac{{14 - 5m}}{{m - 4}}} \right)\]
Để (d1) và (d2) tại một điểm nằm trên trục hoành thì \[\frac{{14 - 5m}}{{m - 4}} = 0\]
\[ \Leftrightarrow 14 - 5m = 0 \Leftrightarrow m = \frac{{14}}{5}\left( {tm} \right)\]
Vậy \(m = \frac{{14}}{5}\).
Câu 11:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(– 4; 1); B(2; 4); C(2; –2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho.
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: B
Gọi I(x; y)
Ta có
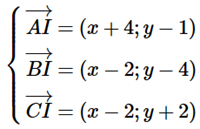
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên
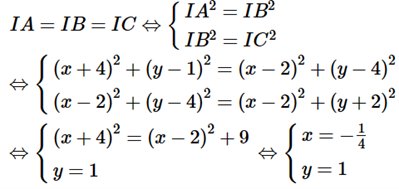
Câu 12:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Bất phương trình (2) ⇔ (x + 1)(3x – 4) ≤ 0 \( \Leftrightarrow - 1 \le x \le \frac{4}{3}\)
Suy ra \({S_2} = \left[ { - 1;\frac{4}{3}} \right]\)
Bất phương trình (1) ⇔ 2x < – m \( \Leftrightarrow x < \frac{{ - m}}{2}\)
Suy ra \({S_1} = \left( { - \infty ; - \frac{m}{2}} \right)\)
Để hệ bất phương trình vô nghiệm khi và chỉ khi S1 ∩ S2 = ∅
\( \Leftrightarrow \frac{{ - m}}{2} \le 1\)
⇔ m ≥ 2.
Vậy ta chọn đáp án C.
Câu 13:
 Xem đáp án
Xem đáp án
Lời giải
Ta có
\(4 = 5 - 1 = \sqrt {25} - 1\)
\(2\sqrt 6 - 1 = \sqrt {24} - 1\)
Vì \(\sqrt {25} > \sqrt {24} \)
Nên \(4 > 2\sqrt 6 - 1\)
Vậy \(4 > 2\sqrt 6 - 1\).
Câu 14:
Chứng minh MBOQ và NCOP là các tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
Lời giải
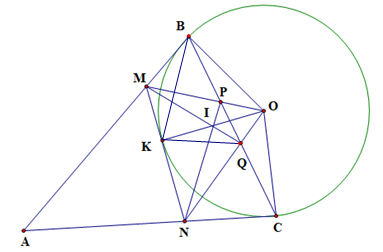
Vì AB, AC là tiếp tuyến của (O) nên \(\widehat {ABO} = \widehat {AC{\rm{O}}} = 90^\circ \).
Vì MN là tiếp tuyến của (O) tại tiếp điểm K nên \(\widehat {OKM} = 90^\circ \).
Xét tứ giác MBOK có: \(\widehat {OBM} = \widehat {OKM} = 90^\circ \), mà hai góc này ở vị trí đối nhau trong tứ giác
Þ tứ giác MBOK nội tiếp.
\( \Rightarrow \widehat {MKB} = \widehat {MOB}\) (hai góc nội tiếp cùng chắn cung MB). (1)
Ta có: NK, NC là hai tiếp tuyến của (O) cắt nhau tại N
Þ NK = NC và NQ là tia phân giác của \(\widehat {KNC}\)
Từ đó DNKQ = DNCQ (c.g.c)
\( \Rightarrow \widehat {NKQ} = \widehat {NCQ}\) (hai góc tương ứng)
Lại có \(\widehat {NCQ} = \widehat {ACB} = \widehat {ABC}\) (do DABC cân tại A vì AB = AC)
\( \Rightarrow \widehat {NKQ} = \widehat {ABC}\) hay \(\widehat {NKQ} = \widehat {MBQ}\).
Mà \(\widehat {NKQ} + \widehat {MKQ} = 180^\circ \Rightarrow \widehat {MBQ} + \widehat {MKQ} = 180^\circ \)
Xét tứ giác MBQK có: \(\widehat {MBQ} + \widehat {MKQ} = 180^\circ \) và hai góc này ở vị trí đối nhau trong tứ giác
Þ tứ giác MBQK nội tiếp
\( \Rightarrow \widehat {MKB} = \widehat {MQB}\) (hai góc nội tiếp cùng chắn cung MB). (2)
Từ (1) và (2) suy ra \(\widehat {MQB} = \widehat {MOB}\).
Þ tứ giác MBOQ nội tiếp.
Chứng minh tương tự ta cũng có: tứ giác NCOP là tứ giác nội tiếp.
Câu 15:
 Xem đáp án
Xem đáp án
Lời giải
Hàm số bậc nhất cần tìm có dạng y = ax + b (a ≠ 0)
Vì hàm số có hệ số góc bằng –2 nên ta có: y = –2x + b
Vì đồ thị hàm số đi qua điểm M(1; 3) nên:
3 = –2.1 + b ⇔ b = 5
Vậy hàm số cần tìm là y = –2x + 5.
Câu 16:
Tìm số hạng không chứa x trong khai triển:
a) \({\left( {x + \frac{1}{{{x^4}}}} \right)^{10}}\);
b) \({\left( {{x^2} + \frac{1}{{{x^4}}}} \right)^{12}}\).
 Xem đáp án
Xem đáp án
Lời giải
a) Ta có \[{\left( {x + \frac{1}{{{x^4}}}} \right)^{10}} = \sum\limits_{k = 0}^{10} {C_{10}^k.{x^{10 - k}}.{{\left( {\frac{1}{{{x^4}}}} \right)}^k}} = \sum\limits_{k = 0}^{10} {C_{10}^k.{x^{10 - k - 4k}}} = \sum\limits_{k = 0}^{10} {C_{10}^k.{x^{10 - 5k}}} \]
Số hạng không chứa x là số hạng có lũy thừa của x bằng 0 nên ta có:
10 – 5k = 0 Û k = 2.
Vậy số hạng không chứa x trong khai triển là \(C_{10}^2 = 45\).
b) Ta có \[{\left( {{x^2} + \frac{1}{{{x^4}}}} \right)^{12}} = \sum\limits_{k = 0}^{12} {C_{12}^k.{x^{2.\left( {12 - k} \right)}}.{{\left( {\frac{1}{{{x^4}}}} \right)}^k}} = \sum\limits_{k = 0}^{12} {C_{12}^k.{x^{24 - 2k - 4k}}} = \sum\limits_{k = 0}^{12} {C_{12}^k.{x^{24 - 6k}}} \]
Số hạng không chứa x là số hạng có lũy thừa của x bằng 0 nên ta có:
24 – 6k = 0 Û k = 4
Vậy số hạng không chứa x trong khai triển là \(C_{12}^4 = 495\).
Câu 17:
Cho 7 điểm A, B, C, D, E, F, G. Chứng minh
a) \(\overrightarrow {AB} + \overrightarrow {C{\rm{D}}} + \overrightarrow {EF} + \overrightarrow {GA} = \overrightarrow {CB} + \overrightarrow {E{\rm{D}}} + \overrightarrow {GF} \).
b) \(\overrightarrow {AB} - \overrightarrow {AF} + \overrightarrow {C{\rm{D}}} - \overrightarrow {CB} + \overrightarrow {EF} - \overrightarrow {E{\rm{D}}} = \overrightarrow 0 \).
 Xem đáp án
Xem đáp án
Lời giải
a) Ta có
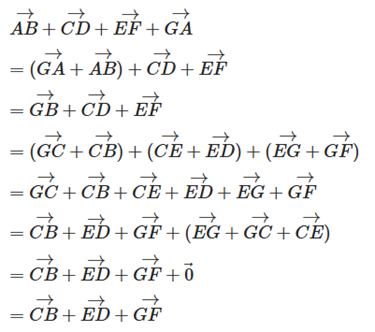
b) Ta có
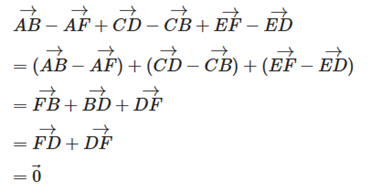
Câu 18:
Cho tam giác ABC có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng bốn điểm A; D; H; E cùng nằm trên một đường tròn (gọi tâm của nó là O).
b) Gọi M là trung điểm của BC. Chứng minh ME là tiếp tuyến đường tròn (O).
 Xem đáp án
Xem đáp án
Lời giải
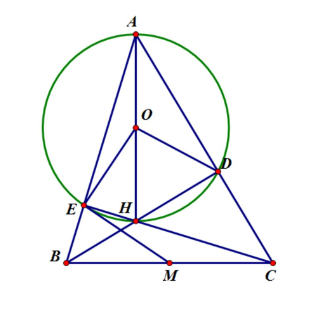
a) Gọi O là trung điểm của AH
Xét tam giác AEH vuông tại H có EO là trung tuyến
Suy ra AO = OH = OE
Xét tam giác ADH vuông tại H có DO là trung tuyến
Suy ra AO = OH = OD
Do đó OA = OH = OD = OE
Vậy bốn điểm A; D; H; E cùng nằm trên một đường tròn tâm O
b) Xét tam giác ABC có hai đường cao BD và CE cắt nhau tại H
Suy ra H là trực tâm
Do đó AH ⊥ BC
Mà CE ⊥ AB
Suy ra \(\widehat {E{\rm{A}}H} = \widehat {ECB}\) (1)
Ta có OA = OE nên tam giác OAE cân tại O
Suy ra \(\widehat {E{\rm{AO}}} = \widehat {OEA}\) (2)
Xét tam giác EBC vuông tại E có EM là trung tuyến
Suy ra EM = MC nên tam giác MCE cân tại M
Suy ra \(\widehat {MEC} = \widehat {MCE}\) (3)
Từ (1), (2) và (3) ta có \(\widehat {MEC} = \widehat {A{\rm{E}}O}\)
Mà \(\widehat {OEC} + \widehat {A{\rm{E}}O} = \widehat {A{\rm{E}}C} = 90^\circ \)
Suy ra \(\widehat {OEC} + \widehat {MEC} = \widehat {OEM} = 90^\circ \), hay OE ⊥ EM
Xét (O) có OE ⊥ EM, OE là bán kính
Suy ra ME là tiếp tuyến đường tròn (O)
Vậy ME là tiếp tuyến đường tròn (O).
Câu 19:
 Xem đáp án
Xem đáp án
Lời giải
Cách 1:
Ta có: hệ số góc của đường thẳng y = x – 2 là a = 1.
Do đó tanα = 1 Þ α = 45°.
Cách 2:
Xét đường thẳng y = x – 2.
Cho y = 0 suy ra x = 2 ta có A(2; 0).
Cho x = 0 suy ra y = – 2 ta có B(0; – 2).
Vẽ đường thẳng đi qua A và B ta được đồ thị hàm số y = x – 2.
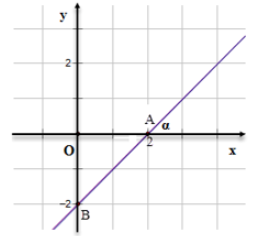
Ta có OA = 2, OB = 2
Xét tam giác OAB vuông tại O có: \(\tan \widehat {OAB} = \frac{{OB}}{{OA}} = \frac{2}{2} = 1\)
\( \Rightarrow \widehat {OAB} = 45^\circ \Rightarrow \alpha = 45^\circ \)
Vậy α = 45°.
Câu 20:
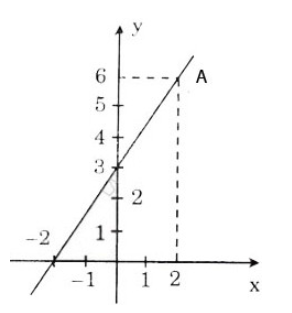
Cho hàm số bậc nhất y = ax + 3.
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2; 6).
b) Vẽ đồ thị của hàm số với hệ số a tìm được ở câu a.
 Xem đáp án
Xem đáp án
Lời giải
a) Đồ thị hàm số đi qua điểm A(2; 6)
Suy ra 6 = 2a + 3
Hay \(a = \frac{3}{2}\).
b) Đồ thị hàm số \(y = \frac{3}{2}x + 3\) đi qua các điểm A(– 2; 0) và B(0; 3)
Ta có đồ thị
Câu 21:
Cho tam giác ABC. Gọi P, Q, R lần lượt là trung điểm của các cạnh BC, CA, AB.
a) Xác định điểm N thỏa mãn \(\overrightarrow {NA} + \overrightarrow {NB} + 2\overrightarrow {NC} = \overrightarrow 0 \).
b) Phân tích \(\overrightarrow {AM} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \) với M ∈ BC thỏa mãn \(\overrightarrow {BM} = \frac{2}{5}\overrightarrow {BC} \).
c) Với điểm O bất kì, chứng minh \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {ON} \).
 Xem đáp án
Xem đáp án
Lời giải
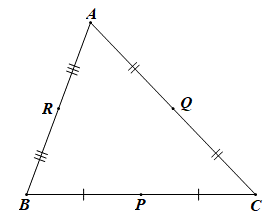
a) Do R là trung điểm của AB nên \(\overrightarrow {NA} + \overrightarrow {NB} = 2\overrightarrow {N{\rm{R}}} \)
Ta có \(\overrightarrow {NA} + \overrightarrow {NB} + 2\overrightarrow {NC} = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {NR} + 2\overrightarrow {NC} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {NR} + \overrightarrow {NC} = \overrightarrow 0 \)
Suy ra N là trung điểm của CR.
b) Ta có\(\overrightarrow {BM} = \frac{2}{5}\overrightarrow {BC} \)
\( \Leftrightarrow \overrightarrow {BA} + \overrightarrow {AM} = \frac{2}{5}\overrightarrow {BA} + \frac{2}{5}\overrightarrow {AC} \)
\( \Leftrightarrow \overrightarrow {AM} = \frac{2}{5}\overrightarrow {BA} + \frac{2}{5}\overrightarrow {AC} - \overrightarrow {BA} \)
\( \Leftrightarrow \overrightarrow {AM} = \frac{3}{5}\overrightarrow {AB} + \frac{2}{5}\overrightarrow {AC} \).
c) Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = \overrightarrow {ON} + \overrightarrow {NA} + \overrightarrow {ON} + \overrightarrow {NB} + 2\overrightarrow {ON} + 2\overrightarrow {NC} \)
\( = 4\overrightarrow {ON} + \overrightarrow {NA} + + \overrightarrow {NB} + 2\overrightarrow {NC} = 4\overrightarrow {ON} \) (vì \(\overrightarrow {NA} + \overrightarrow {NB} + 2\overrightarrow {NC} = \overrightarrow 0 \))
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {ON} \).
Câu 22:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H lên AB, AC.
a) Chứng minh AD . AB = AE . AC.
b) Chứng minh \(\frac{{BH}}{{HC}} = {\left( {\frac{{AB}}{{AC}}} \right)^2}\).
c) Cho BH = 4 cm, CH = 9 cm. Tính DE và \(\widehat {A{\rm{D}}E}\) (làm tròn đến độ).
d) Gọi M là trung điểm của BH, N là trung điểm của CH. Tính SDENM.
 Xem đáp án
Xem đáp án
Lời giải
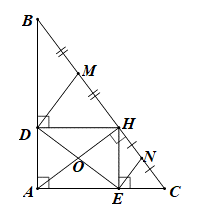
a) Xét ΔABH vuông tại H có HD ⊥ AB
Suy ra AH2 = AD . AB (hệ thức lượng trong tam giác vuông)
Xét ΔAEH vuông tại H có HE ⊥ AC
Suy ra AH2 = AE . AC (hệ thức lượng trong tam giác vuông)
Mà AH2 = AD . AB (chứng minh trên)
Suy ra AD . AB = AE . AC
b) Vì ΔABC vuông tại A nên AB2 + AC2 = BC2 (định lý Pytago)
Xét ΔABC vuông tại A có AH ⊥ BC
Suy ra AB2 = BH . BC (hệ thức lượng trong tam giác vuông)
⇔ AB2 . BC = BH . BC2
\( \Leftrightarrow \frac{{BH}}{{BC}} = \frac{{A{B^2}}}{{B{C^2}}}\)
\( \Leftrightarrow \frac{{BH}}{{BC - BH}} = \frac{{A{B^2}}}{{B{C^2} - A{B^2}}}\)
\( \Leftrightarrow \frac{{BH}}{{HC}} = \frac{{A{B^2}}}{{A{C^2}}} = {\left( {\frac{{AB}}{{AC}}} \right)^2}\)
c) Xét ΔABC vuông tại A có AH ⊥ BC
Suy ra AH2 = BH . HC (hệ thức lượng trong tam giác vuông)
Hay AH2 = 4 . 9 = 36
Suy ra AH = 6
Xét tứ giác ADHE có \(\widehat {DAE} = \widehat {A{\rm{D}}H} = \widehat {A{\rm{E}}H} = 90^\circ \)
Suy ra ADHE là hình chữ nhật
Mà AH, DE là hai đường chéo
Suy ra DE = AH = 6 (cm)
Vì ΔABH vuông tại H nên HB2 + AH2 = BA2 (định lý Pytago)
Hay 42 + 62 = AB2
Suy ra \(AB = 2\sqrt {13} \)
Xét ΔABH vuông tại H có HD ⊥ AB
Suy ra AH2 = AD . AB (hệ thức lượng trong tam giác vuông)
Hay \({6^2} = A{\rm{D }}.{\rm{ }}2\sqrt {13} \)
Suy ra \(A{\rm{D = }}\frac{{18}}{{\sqrt {13} }}\)
Xét tam giác ADE vuông tại A có
\({\rm{cos}}\widehat {A{\rm{D}}E} = \frac{{A{\rm{D}}}}{{DE}} = \frac{{18}}{{6\sqrt {13} }} = \frac{3}{{\sqrt {13} }}\)
Suy ra \(\widehat {A{\rm{D}}E} \approx 33^\circ \).
d) Vì ra ADHE là hình chữ nhật có AH, DE là hai đường chéo
Suy ra AH cắt DE tại trung điểm O của mỗi đường
Mà AH = DE
Do đó OH = OD
Suy ra tam giác OHD cân tại O
Suy ra \(\widehat {OH{\rm{D}}} = \widehat {O{\rm{D}}H}\)
Xét ΔHBD vuông tại D có DM là đường trung tuyến ứng với cạnh huyền
Suy ra \(DM = MH = \frac{1}{2}BH = \frac{1}{2}.4 = 2\)
Do đó ΔDMH cân tại M
Suy ra \(\widehat {MDH} = \widehat {MH{\rm{D}}}\)
Mà \(\widehat {DHA} + \widehat {MH{\rm{D}}} = \widehat {AHB} = 90^\circ \) và \(\widehat {AH{\rm{D}}} = \widehat {{\rm{ED}}H}\)(chứng minh trên)
Suy ra \(\widehat {H{\rm{D}}E} + \widehat {M{\rm{DH}}} = \widehat {M{\rm{D}}E} = 90^\circ \)
Hay MD ⊥ DE.
Chứng minh tương tự ta có \(EN = \frac{{CH}}{2} = \frac{9}{2} = 4,5\)
và \(\widehat {DEH} + \widehat {HEN} = \widehat {AHE} + \widehat {{\rm{EHN}}} = \widehat {AHC} = 90^\circ \)
Hay \(\widehat {DEN} = 90^\circ \)
Suy ra EN ⊥ DE
Mà MD ⊥ DE
Nên EN // MD (quan hệ từ vuông góc đến song song)
Xét tứ giác DENM có EN ⊥ DE, EN // MD (chứng minh trên)
Suy ra DENM là hình thang vuông
Do đó \({S_{DENM}} = \frac{{\left( {DM + EN} \right).DE}}{2} = \frac{{\left( {2 + 4,5} \right).6}}{2} = 19,5\,\,\left( {c{m^2}} \right)\) .
Câu 23:
 Xem đáp án
Xem đáp án
Lời giải
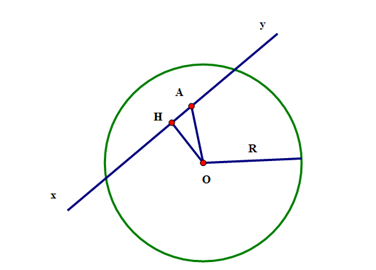
Kẻ OH vuông góc với xy
Vì tam giác OAH vuông tại H, suy ra OH ≤ OA
Mặt khác A nằm trong đường tròn (O;R) nên OA ≤ R.
Vậy đường thẳng xy và đường tròn (O; R) cắt nhau.
Câu 24:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: B
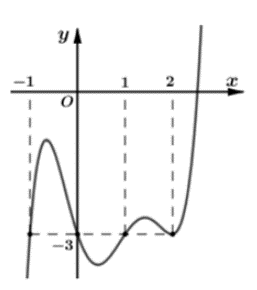
Xét hàm số h(x) = f(x) + 3x, x ∈ ℝ
h’(x) = f’(x) + 3, x ∈ R
h’(x) = 0 ⇔ f’(x) = – 3
⇔ x ∈ { – 1; 0; 1; 2}
Với x = 2 là nghiệm kép vì qua nghiệm x = 2 thì h’(x) không đổi dấu
Dựa vào đồ thị của f’(x) ta có
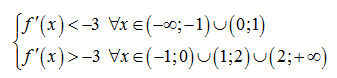
Mà h(0) = f(0) + 3 . 0 = f(0) < 0
Bảng biến thiên của hàm số h(x) = f(x) + 3x
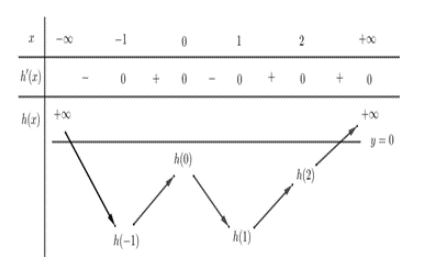
Từ đó suy ra bảng biến thiên của hàm số g(x) = | f(x) + 3x | = | h(x) |
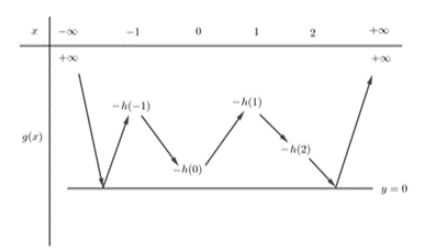
Từ bảng biến thiên ta thấy hàm số có 5 điểm cực trị
Vậy ta chọn đáp án B.
Câu 25:
Cho hình bình hành ABCD. Hai đầu M, N lần lượt là trung điểm của BC và AD. Tìm các tổng:
a) \(\overrightarrow {NC} + \overrightarrow {MC} ,\overrightarrow {AM} + \overrightarrow {C{\rm{D}}} ,\overrightarrow {A{\rm{D}}} + \overrightarrow {NC} \).
b) \(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {{\rm{AD}}} \).
 Xem đáp án
Xem đáp án
Lời giải
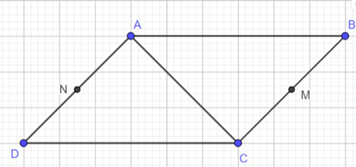
Ta có:
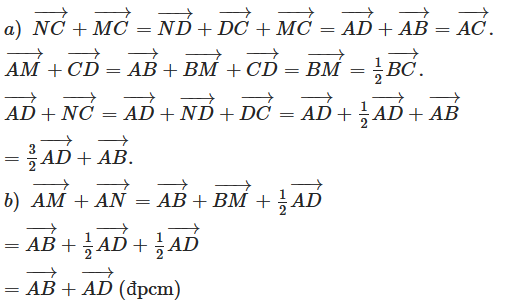
Câu 26:
 Xem đáp án
Xem đáp án
Lời giải
Ta có x4 + 3x3 – x – 3 = 0
⇔ x3(x + 3) – (x + 3) = 0
⇔ (x + 3)(x3 – 1) = 0
\[ \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\{x^3} - 1 = 0\end{array} \right.\]
\( \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 1\end{array} \right.\)
Vậy x = 1 hoặc x = – 3.
Câu 27:
Cho hàm số \(y = f(x) = \sqrt x + \sqrt {1 - x} \)
Tìm x biết:
a) f(x) = 1;
b) f(x) = 0,5.
 Xem đáp án
Xem đáp án
Lời giải
Điều kiện xác định 0 ≤ x ≤ 1
a) Với f(x) = 1 thì \(\sqrt x + \sqrt {1 - x} = 1\)
\( \Leftrightarrow {\left( {\sqrt x + \sqrt {1 - x} } \right)^2} = 1\)
\( \Leftrightarrow x + 1 - x + 2\sqrt {x(1 - x)} = 1\)
\( \Leftrightarrow 2\sqrt {x(1 - x)} = 0\)
⇔ x(1 – x) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Vậy x ∈ {0; 1}.
b) Với f(x) = 0,5 thì \(\sqrt x + \sqrt {1 - x} = 0,5\)
\( \Leftrightarrow {\left( {\sqrt x + \sqrt {1 - x} } \right)^2} = {0,5^2}\)
\( \Leftrightarrow x + 1 - x + 2\sqrt {x(1 - x)} = 0,25\)
\( \Leftrightarrow 2\sqrt {x(1 - x)} = - 0,75\) (vô nghiệm)
Vậy x ∈ ∅.
Câu 28:
Cho tam giác ABC. Gọi M là điểm trên BC sao cho MB = 2MC. Chứng minh
\(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \) .
 Xem đáp án
Xem đáp án
Lời giải
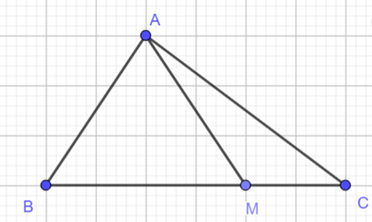
Vì M nằm trên BC sao cho MB = 2MC
Suy ra \(BM = \frac{2}{3}BC\)
Ta có \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \)

Vậy \(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \).
Câu 29:
 Xem đáp án
Xem đáp án
Lời giải
Với x = 0 thì y = 3 Þ điểm (0; 3) thuộc (d).
Với x = –1 thì y = 1 Þ điểm (–1; 1) thuộc (d).
Đồ thị hàm số y = 2x + 3 đi qua hai điểm (0; 3) và (–1; 1)
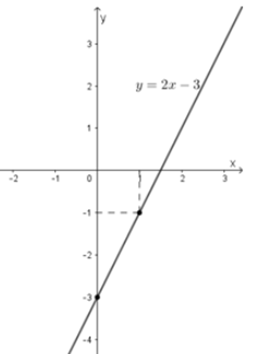
Giao điểm của (d) với trục hoành có tung độ bằng 0 nên y = 0
Khi đó 2x + 3 = 0
Hay \(x = \frac{{ - 3}}{2}\)
Giao điểm của (d) với trục tung có hoành độ bằng 0 nên x = 0
Khi đó 2 . 0 + 3 = y
Hay y = 3
Vậy giao điểm của (d) với trục hoành là \(\left( {\frac{{ - 3}}{2};0} \right)\), với trục tung là (0; 3).
Câu 30:
Cho tam giác ABC cân tại A có các đường cao AH và BK cắt nhau tại I. Chứng minh:
a) Đường tròn đường kính AI đi qua K.
b) HK là tiếp tuyến của đường tròn đường kính AI.
 Xem đáp án
Xem đáp án
Lời giải
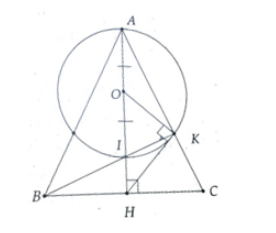
a) Vì BK là đường cao của tam giác ABC nên \(\widehat {AKB} = 90^\circ \)
Suy ra tam giác AKI vuông tại K
Do đó K thuộc đường tròn đường kính AI
b) Gọi O là trung điểm của AI
Vì OA = OK nên tam giác OAK cân tại O
Suy ra \(\widehat {OAK} = \widehat {OK{\rm{A}}}\)
Vì tam giác BCK vuông ở K nên \(\widehat {KBC} + \widehat {KCB} = 90^\circ \) (trong tam giác vuông tổng hai góc nhọn bằng 90°)
Vì tam giác ACH vuông ở H nên \(\widehat {HAC} + \widehat {HCA} = 90^\circ \) (trong tam giác vuông tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {KBC} = \widehat {HAC}\)
Mà \(\widehat {OAK} = \widehat {OK{\rm{A}}}\) (chứng minh trên)
Suy ra \(\widehat {KBC} = \widehat {OK{\rm{A}}}\) (1)
Vì tam giác ABC cân tại A, AH là đường cao
Nên AH là đường trung tuyến
Hay H là trung điểm của BC
Xét tam giác BCK vuông ở K có KH là trung tuyến
Suy ra BH = HK
Do đó tam giác BHK cân tại H
Suy ra \(\widehat {BHK} = \widehat {BKH}\) (2)
Từ (1) và (2) suy ra \(\widehat {AKO} = \widehat {BKH}\)
Mà \(\widehat {AKO} + \widehat {OKB} = \widehat {AKB} = 90^\circ \)
Suy ra \(\widehat {BKO} + \widehat {BKH} = 90^\circ \)
Hay \(\widehat {HOK} = 90^\circ \)
Xét (O) có OH ⊥ HK
Suy ra HK là tiếp tuyến của (O)
Vậy HK là tiếp tuyến của đường tròn đường kính AI.
Câu 31:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Ta có \(\overrightarrow {IA} + 2\overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {IA} + 2\overrightarrow {IA} + 2\overrightarrow {AB} + 3\overrightarrow {IA} + 3\overrightarrow {AC} = \overrightarrow 0 \)
\( \Leftrightarrow 6\overrightarrow {IA} + 2\overrightarrow {AB} + 3\overrightarrow {AC} = \overrightarrow 0 \)
\( \Leftrightarrow 6\overrightarrow {IA} = - 2\overrightarrow {AB} - 3\overrightarrow {AC} \)
\( \Leftrightarrow \overrightarrow {AI} = \frac{1}{3}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \)
Vậy ta chọn đáp án C.
Câu 32:
Cho tam giác ABC nội tiếp đường tròn tâm O trực tâm H đường kính AD
a) Chứng minh \(\overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {H{\rm{D}}} \).
b) Gọi M là trung điểm BC. Chứng minh \(\overrightarrow {AH} = 2\overrightarrow {OM} \).
c) Gọi H' là điểm đối xứng với H qua O. Chứng minh \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HH'} \).
d) Gọi D' là điểm đối xứng với B qua O. Chứng minh \(\overrightarrow {AH} = \overrightarrow {D'C} \).
 Xem đáp án
Xem đáp án
Lời giải
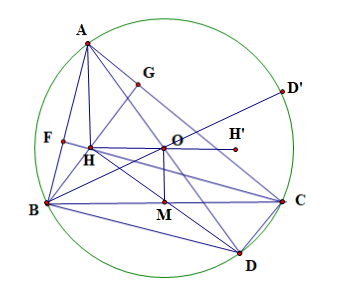
a) Kẻ đường cao BG, CF của tam giác ABC
Vì H là trực tâm nên H là giao điểm của BG và CF
Vì tam giác ABD nội tiếp (O) đường kính AD
Nên tam giác ABD vuông tại B, suy ra AB ⊥ BD
Mà AB ⊥ CF, do đó BD // CF (quan hệ từ vuông góc đến song song)
Vì tam giác ACD nội tiếp (O) đường kính AD
Nên tam giác ACD vuông tại C, suy ra AC ⊥ CD
Mà AC ⊥ BG, do đó BG // CD (quan hệ từ vuông góc đến song song)
Xét tứ giác BHCD có
BD // CF (chứng minh trên);
BG // CD (chứng minh trên)
Suy ra BHCD là hình bình hành
Do đó \(\overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {H{\rm{D}}} \).
b) Xét hình bình hành BHCD có M là trung điểm BC
BC, HD là hai đường chéo
Suy ra M là trung điểm của HD
Xét tam giác AHD có O là trung điểm của AD, M là trung điểm của HD
Suy ra OM là đường trung bình
Do đó \(OM = \frac{1}{2}AH\)
Suy ra \(\overrightarrow {AH} = 2\overrightarrow {OM} \)
c) Ta có \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HO} + \overrightarrow {OA} + \overrightarrow {HO} + \overrightarrow {OB} + \overrightarrow {HC} \)
\( = 2\overrightarrow {HO} + \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {HC} = 2\overrightarrow {HO} + \overrightarrow {DO} + \overrightarrow {OB} + \overrightarrow {HC} \)
\( = 2\overrightarrow {HO} + \overrightarrow {DB} + \overrightarrow {HC} = 2\overrightarrow {HO} = \overrightarrow {HH'} \)
Vậy \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HH'} \).
d) Xét (O) có △BCD’ và △BAD’ nội tiếp (O) đường kính BD’
Suy ra △BCD’ vuông tại A và △BAD’ vuông tại C
Khi đó AB ⊥ AD’ và BC ⊥ CD’
Ta có AB ⊥ CH, AB ⊥ AD’ nên CH // AD’ (quan hệ từ vuông góc đến song song)
Ta có BC ⊥ AH, BC ⊥ CD’ nên AH // CD’ (quan hệ từ vuông góc đến song song)
Xét tứ giác AHCD’ có
CH // AD’ và AH // CD’ (chứng minh trên)
Suy ra AHCD’ là hình bình hành
Do đó AH = D’C
Suy ra \(\overrightarrow {AH} = \overrightarrow {D'C} \).Câu 33:
Cho đường tròn (O; R), đường kính AB. Vẽ dây AC sao cho \(\widehat {CAB} = 30^\circ \). Trên tia đối của tia BA, lấy điểm M sao cho BM = R. Chứng minh:
a) MC là tiếp tuyến của đường tròn (O).
b) MC2 = 3R2.
 Xem đáp án
Xem đáp án
Lời giải
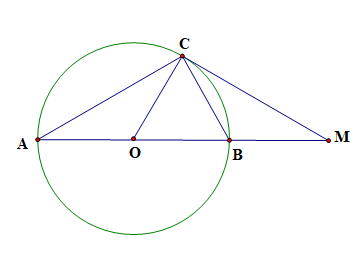
Ta có BM = R
OA = OB = R
B nằm giữa M và O (vì M thuộc tia đối của tia BA)
Suy ra B là trung điểm của OM
Vì tam giác ABC nội tiếp (O) đường kính AB
Nên tam giác ABC vuông tại C
Suy ra \(\widehat {CAB} + \widehat {CBA} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà \(\widehat {CAB} = 30^\circ \), nên \(\widehat {CBA} = 60^\circ \)
Lại có tam giác OBC cân tại O (vì OB = OC)
Suy ra tam giác OBC đều. Do đó OB = CB, \(\widehat {COB} = 60^\circ \)
Mà OB = BM, suy ra \[{\rm{OB }} = BM = CM = \frac{1}{2}OM\]
Xét tam giác OCM có
\[{\rm{OB }} = BM = CM = \frac{1}{2}OM\]
CM là trung tuyến
Suy ra tam giác OCM vuông tại C
Do đó CO ⊥ CM
Xét (O) có CO ⊥ CM (chứng minh trên)
MC là tiếp tuyến của đường tròn (O)
b) Xét tam giác OCM vuông ở C có \(\widehat {COM} + \widehat {CMO} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà \(\widehat {COM} = 60^\circ \), nên \(\widehat {CMO} = 30^\circ \)
Suy ra \(\widehat {CMO} = \widehat {CAM}\left( { = 30^\circ } \right)\)
Xét DMCB và DMAC có
\(\widehat {CMO} = \widehat {CAM}\) (chứng minh trên)
\(\widehat M\) là góc chung
Suy ra (g.g)
Do đó \(\frac{{MC}}{{MA}} = \frac{{MB}}{{MC}}\)
Suy ra MC2 = MA . MB = (OA + OB + BM) . MB = 3R . R = 3R2.
Câu 34:
 Xem đáp án
Xem đáp án
Lời giải
Ta có không gian mẫu W = {SS; NN; SN; NS}.
Suy ra n(Ω) = 4
Gọi biến cố xuất hiện hai mặt ngửa là A.
Do đó A = {NN}, suy ra n(A) = 1.
Vậy xác suất để xuất hiện hai mặt ngửa là \(\frac{1}{4}\).
Câu 35:
Cho hệ phương trình: \(\left\{ \begin{array}{l}3x + 4y = 12\\mx + 2y = 6\end{array} \right.\).
a) Giải hệ phương trình với m = 1.
b) Tìm m để hệ phương trình có nghiệm x ∈ ℝ .
 Xem đáp án
Xem đáp án
Lời giải
Với m = 1 ta có hệ phương trình:
\[\left\{ \begin{array}{l}3x + 4y = 12\\x + 2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 4y = 12\\3x + 6y = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 4y = 12\\2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 4y = 12\\y = 3\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}3x + 4.3 = 12\\y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 0\\y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 3\end{array} \right.\]
Vậy với m = 1 thì hệ phương trình có nghiệm duy nhất (x; y) = (0; 3).
b) Ta có:
\(\left\{ \begin{array}{l}3x + 4y = 12\\mx + 2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 4y = 12\\2mx + 4y = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 4y = 12\\\left( {2m - 3} \right)x = 0\left( * \right)\end{array} \right.\)
Để hệ phương trình có nghiệm x ∈ ℝ thì phương trình (*) có nghiệm x ∈ ℝ
Û 2m – 3 = 0 \( \Leftrightarrow m = \frac{3}{2}\).
Câu 36:
Giải hệ phương trình:
a) \(\left\{ \begin{array}{l}{x^3} + {y^3} = 1\\{x^2}y + 2{\rm{x}}{y^2} + {y^3} = 2\end{array} \right.\).
b) \(\left\{ \begin{array}{l}{y^2} = \left( {x + 8} \right)\left( {{x^2} + 2} \right)\\{y^2} - 4\left( {{\rm{x + 2}}} \right)y + 16 + 16{\rm{x}} - 5{{\rm{x}}^2} = 0\end{array} \right.\).
 Xem đáp án
Xem đáp án
Lời giải
a) Ta có \(\left\{ \begin{array}{l}{x^3} + {y^3} = 1\\{x^2}y + 2{\rm{x}}{y^2} + {y^3} = 2\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2{x^3} + 2{y^3} = 2\\{x^2}y + 2{\rm{x}}{y^2} + {y^3} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^3} + {y^3} = 1\\2{{\rm{x}}^3} + {y^3} - {x^2}y - 2{\rm{x}}{y^2} = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x^3} + {y^3} = 1\\{{\rm{x}}^2}\left( {2{\rm{x}} - y} \right) + {y^2}\left( {y - 2{\rm{x}}} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^3} + {y^3} = 1\\\left( {2{\rm{x}} - y} \right)\left( {{x^2} - {y^2}} \right) = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x^3} + {y^3} = 1\\\left( {2{\rm{x}} - y} \right)\left( {x - y} \right)\left( {x + y} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^3} + {y^3} = 1\\\left[ \begin{array}{l}2{\rm{x}} - y = 0\\x - y = 0\\x + y = 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x^3} + {y^3} = 1\\\left[ \begin{array}{l}2{\rm{x = y}}\\x = y\\x = - y\end{array} \right.\end{array} \right.\)
• \[\left\{ \begin{array}{l}{x^3} + {y^3} = 1\\y = 2{\rm{x}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^3} + 8{{\rm{x}}^3} = 1\\y = 2{\rm{x}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \sqrt[3]{{\frac{1}{9}}}\\y = 2{\rm{x}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \sqrt[3]{{\frac{1}{9}}}\\y = 2\sqrt[3]{{\frac{1}{9}}}\end{array} \right.\]
Þ Hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\sqrt[3]{{\frac{1}{9}}};2\sqrt[3]{{\frac{1}{9}}}} \right)\).
• \(\left\{ \begin{array}{l}{x^3} + {y^3} = 1\\x = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{{\rm{x}}^3} = 1\\x = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\rm{x}} = \sqrt[3]{{\frac{1}{2}}}\\x = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\rm{x}} = \sqrt[3]{{\frac{1}{2}}}\\y = \sqrt[3]{{\frac{1}{2}}}\end{array} \right.\)
Þ Hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\sqrt[3]{{\frac{1}{2}}};\sqrt[3]{{\frac{1}{2}}}} \right)\).
• \[\left\{ \begin{array}{l}{x^3} + {y^3} = 1\\x = - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - {y^3} + {y^3} = 1\\x = - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0{y^3} = 1\left( {v\^o {\rm{ }}l\'i } \right)\\x = - y\end{array} \right.\]
Vậy hệ phương trình đã cho có tập nghiệm là \(S = \left\{ {\left( {\sqrt[3]{{\frac{1}{9}}};2\sqrt[3]{{\frac{1}{9}}}} \right);\left( {\sqrt[3]{{\frac{1}{2}}};\sqrt[3]{{\frac{1}{2}}}} \right)} \right\}\).
b) \(\left\{ \begin{array}{l}{y^2} = \left( {x + 8} \right)\left( {{x^2} + 2} \right)\\{y^2} - 4\left( {{\rm{x + 2}}} \right)y + 16 + 16{\rm{x}} - 5{{\rm{x}}^2} = 0\end{array} \right.\)
Ta có
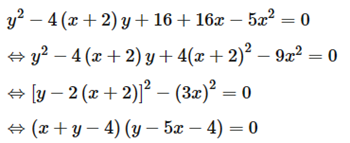
⇔ \(\left[ \begin{array}{l}x + y - 4 = 0\\y - 5{\rm{x}} - 4 = 0\end{array} \right.\)
⇔ \(\left[ \begin{array}{l}y = 4 - x\\y = 5{\rm{x + }}4\end{array} \right.\)
+) Nếu y = 5x + 4
y2 = (x + 8)(x2 + 2)
⇔ (5x + 4)2 = (x + 8)(x2 + 2)
⇔ 25x2 – 40x + 16 = x3 + 2x + 8x2 + 16
⇔ x3 – 17x2 + 42x = 0
⇔ x(x2 – 17x + 42) = 0
⇔ x(x – 3)(x – 14) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 4\\x = 3 \Rightarrow y = 19\\x = 14 \Rightarrow y = 74\end{array} \right.\)
+) Nếu y = 4 – x
y2 = (x + 8)(x2 + 2)
⇔ (4 – x)2 = (x + 8)(x2 + 2)
⇔ x2 – 8x + 16 = x3 + 2x + 8x2 + 16
⇔ x3 + 7x2 + 10x = 0
⇔ x(x2 + 7x + 10) = 0
⇔ x(x + 2)(x + 5) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 4\\x = - 2 \Rightarrow y = 6\\x = - 5 \Rightarrow y = 9\end{array} \right.\)
Vậy hệ phương trình đã cho có tập nghiệm là S = {(0; 4); (3; 19); (14; 74); (0; 4); (–2; 6); (–5; 9)}.
Câu 37:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \(\frac{{{{\sin }^2}2{\rm{x}} - 4{{\sin }^2}x}}{{{{\sin }^2}2{\rm{x + }}4{{\sin }^2}x - 4}}\)
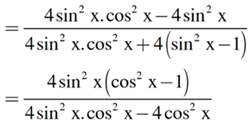
= \(\frac{{ - 4{{\sin }^4}x}}{{ - 4c{\rm{o}}{{\rm{s}}^4}x}} = {\tan ^4}x\)
Vậy \(\frac{{{{\sin }^2}2{\rm{x}} - 4{{\sin }^2}x}}{{{{\sin }^2}2{\rm{x + }}4{{\sin }^2}x - 4}} = {\tan ^4}x\).
Câu 38:
 Xem đáp án
Xem đáp án
Lời giải
Để (d) và (d’) cắt nhau thì m + 2 ≠ 3 Û m ≠ 1.
Hoành độ giao điểm của (d) và (d’) là nghiệm của phương trình
(m + 2)x + 2m2 + 1 = 3x + 3
⇔ (m + 2)x – 3x = 3 – 2m2 – 1
⇔ (m – 1)x = 2 – 2m2
⇔ (m – 1)x = 2(1 – m)(1 + m)
\( \Leftrightarrow x = \frac{{\left( {1 - m} \right)\left( {1 + m} \right)}}{{\left( {m - 1} \right)}} = - m - 1\) (do m ≠ 1)
Hai đường thẳng (d) và (d’) cắt nhau trên trục tung suy ra x = 0
⇔ – 1 – m = 0
⇔ – 1 = m (thỏa mãn)
Vậy m = – 1.
Câu 39:
 Xem đáp án
Xem đáp án
Lời giải
Để d1 và d2 cắt nhau thì 3m ≠ 3 Û m ≠ 1.
Phương trình hoành độ giao điểm của d1 và d2 là:
3mx – m2 = 3x + m – 2
Û (3m – 3)x = m2 + m – 2
\( \Leftrightarrow x = \frac{{{m^2} + m - 2}}{{3m - 3}}\) (do m ≠ 1)
\( \Leftrightarrow x = \frac{{\left( {m - 1} \right)\left( {m + 2} \right)}}{{3\left( {m - 1} \right)}} = \frac{{m + 2}}{3}\)
Để d1 và d2 cắt nhau tại một điểm trên trục tung thì hoành độ giao điểm bằng 0
\( \Leftrightarrow \frac{{m + 2}}{3} = 0 \Leftrightarrow m = - 2\left( {tm} \right)\)
Vậy m = – 2.
Câu 40:
Cho đường tròn tâm O bán kính R và một điểm M nằm ngoài đường tròn. Qua M kẻ tiếp tuyến MA với đường tròn (A là tiếp điểm). Tia Mx nằm giữa MA và MO cắt đường tròn (O; R) tại 2 điểm C và D (C nằm giữa M và D). Gọi I là trung điểm của dây CD, kẻ AH vuông góc với MO tại H.
a) Chứng minh OH . OM không đổi.
b) Chứng minh bốn điểm M, A, I, O cùng thuộc 1 đường tròn.
c) Gọi K là giao điểm của OI với HA. Chứng minh KC là tiếp tuyến của đường tròn (O; R).
 Xem đáp án
Xem đáp án
Lời giải
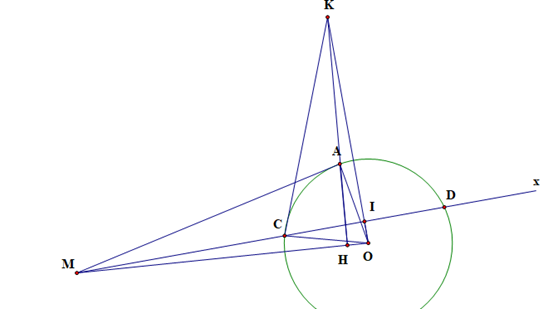
a) Vì MA là tiếp tuyến của (O) nên MA ⊥ OA
Xét tam giác AMO vuông tại A có AH ⊥ OM
Suy ra OH . OM = OA2 = R2
Vì R không đổi nên OH . OM không đổi.
b) Vì OC = OD nên ΔOCD cân tại O
Mà OI là đường trung tuyến, nên OI ⊥ CD
Xét tứ giác OIAM có
\(\widehat {OIM} = \widehat {OAM}\left( { = 90^\circ } \right)\)
Nên OIAM là tứ giác nội tiếp
Vậy bốn điểm M, A, I, O cùng thuộc 1 đường tròn.
c) Xét ΔOHK và ΔOIM có
\(\widehat {OHK} = \widehat {OIM}\left( { = 90^\circ } \right)\)
\(\widehat {HOK}\) là góc chung
Suy ra (g.g)
Do đó \(\frac{{OH}}{{OI}} = \frac{{OK}}{{OM}}\)
Suy ra OI . OK = OH . OM = R2 = OC2
Do đó \(\frac{{OC}}{{OK}} = \frac{{OI}}{{OC}}\)
Xét ΔOCK và ΔOIC có
\(\frac{{OC}}{{OK}} = \frac{{OI}}{{OC}}\)
\(\widehat O\) là góc chung
Suy ra (g.g)
Do đó \(\widehat {OCK} = \widehat {OIC} = 90^\circ \) (hai góc tương ứng)
Hay OC ⊥ OK
Suy ra KC là tiếp tuyến của (O).
Câu 41:
 Xem đáp án
Xem đáp án
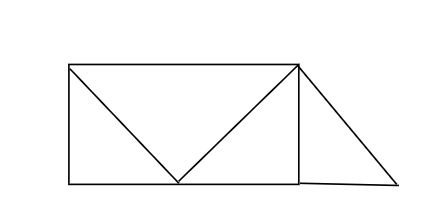
Lời giải
Trong hình vẽ trên có 5 hình tam giác và 5 hình tứ giác
Vậy ta chọn đáp án D.
Câu 42:
Cho hàm số y = (k – 3)x + k’ (d). Tìm các giá trị của k, k’ để đường thẳng (d)
a) Đi qua điểm A(1; 2) và B(– 3; 4).
b) Cắt trục tung tại điểm có tung độ bằng \(1 - \sqrt 2 \) và cắt trục hoành tại điểm có hoành độ \(1 + \sqrt 2 \).
c) Cắt đường thẳng 2y – 4x + 5 = 0.
d) Song song với đường thẳng y – 2x – 1 = 0.
e) Trùng với đường thẳng 3x + y – 5 = 0.
 Xem đáp án
Xem đáp án
Lời giải
a) Đường thẳng (d) đi qua hai điểm A(1; 2) và B(– 3; 4)
\( \Leftrightarrow \left\{ \begin{array}{l}2 = \left( {k - 3} \right).1 + k'\\4 = \left( {k - 3} \right).\left( { - 3} \right) + k'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k + k' = 5\\k' - 3k = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k + k' = 5\\4k = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k' = \frac{5}{2}\\k = \frac{5}{2}\end{array} \right.\)
Vậy hàm số có dạng \(y = \frac{{ - 1}}{2}x + \frac{5}{2}\).
b) Đường thẳng (d) cắt trục tung tại điểm có tung độ bằng \(1 - \sqrt 2 \) và cắt trục hoành tại điểm có hoành độ \(1 + \sqrt 2 \)nên (d) đi qua hai điểm \(\left( {0;1 - \sqrt 2 } \right),\left( {1 + \sqrt 2 ;0} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}1 - \sqrt 2 = \left( {k - 3} \right).0 + k'\\0 = \left( {k - 3} \right).\left( {1 + \sqrt 2 } \right) + k'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k' = 1 - \sqrt 2 \\0 = \left( {1 + \sqrt 2 } \right)k - 3 - 3\sqrt 2 + 1 - \sqrt 2 \end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}k' = 1 - \sqrt 2 \\k = \frac{{2 + 4\sqrt 2 }}{{1 + \sqrt 2 }}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k' = 1 - \sqrt 2 \\k = \frac{{\left( {2 + 4\sqrt 2 } \right)\left( {1 - \sqrt 2 } \right)}}{{1 - 2}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k' = 1 - \sqrt 2 \\k = - 6 + 2\sqrt 2 \end{array} \right.\)
Vậy hàm số có dạng \(y = \left( { - 6 + 2\sqrt 2 } \right)x + 1 - \sqrt 2 \).
c) Ta có 2y – 4x + 5 = 0 \( \Leftrightarrow y = 2{\rm{x}} - \frac{5}{2}\)
Để đường thẳng (d) cắt đường thẳng 2y – 4x + 5 = 0 thì k – 3 ≠ 2
⇔ k ≠ 5.
d) Ta có y – 2x – 1 = 0 ⇔ y = 2x + 1
Để đường thẳng (d) song song với đường thẳng y – 2x – 1 = 0 thì \(\left\{ \begin{array}{l}k - 3 = 2\\k' \ne 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}k = 5\\k' \ne 1\end{array} \right.\).
e) Ta có 3x + y – 5 = 0 ⇔ y = – 3x + 5
Để đường thẳng (d) trùng với đường thẳng 3x + y – 5 = 0 thì \(\left\{ \begin{array}{l}k - 3 = - 3\\k' = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}k = 0\\k' = 5\end{array} \right.\).
Câu 43:
 Xem đáp án
Xem đáp án
Lời giải
Vì diện tích trồng cà rốt gấp 5 lần diên tích trồng hành nên cạnh còn lại của diện tích trồng cà rốt gấp 5 lần cạnh còn lại của phần trồng hành
Cạnh còn lại của diện tích trồng hành là:
936 : 2 : (5 – 1) × 1 = 117 (m)
Cạnh còn lại của diện tích trồng cà rốt là:
117 × 5 = 585 (m)
Chiều dài của mảnh đất ban đầu là:
117 + 585 = 702 (m)
Chu vi mảnh ruộng ban đầu là
(702 + 327) × 2 = 2058 (m) = 205,8 (dam)
Vậy chu vi mảnh ruộng ban đầu là 205,8 dam.
Câu 44:
 Xem đáp án
Xem đáp án
Lời giải
Chiều dài của mảnh vườn đó là:
4 + 4 = 8 (m)
Chu vi của mảnh vườn đó là:
(8 + 4) × 2 = 24 (m)
Vậy chu vi mảnh vườn đó là 24 m.
Câu 45:
Tính nhanh:
a) – (– 2012 + 789) + (– 211) + (– 1012 – 1789).
b) – 72 . 17 + 72 . 31 – 72 . 114.
c) 512 . (2 – 128) – 128 . (– 512)..
d) 120 . (5 – 117) – 117 . (– 120)
 Xem đáp án
Xem đáp án
Lời giải
a) – (– 2012 + 789) + (– 211) + (– 1012 – 1789)
= 2012 – 789 – 211 – 1012 – 1789
= ( 2012 – 1012 ) – 789 – 1789 – 211
= 1000 – 211 – 789 – 1789
= 789 – 789 – 1789
= 0 – 1789
= – 1789.
b) – 72 . 17 + 72 . 31 – 72 . 114
= – 72 . (17 + 114 – 31)
= – 72 . (131 – 31)
= – 72 . 100
= – 7200.
c) 512 . (2 – 128) – 128 . (– 512)
= 512 . 2 – 512 . 128 + 128 . 512
= 512 . 2 + 0
= 1024.
d) 120 . (5 – 117) – 117 . (– 120)
= 120 . 5 – 120 . 117 + 117 . 120
= 120 . 5 – 0
= 600.
Câu 46:
 Xem đáp án
Xem đáp án
Lời giải
Ta có
\(\frac{1}{{1 - x}} + \frac{{2{\rm{x}}}}{{{x^2} - 1}} = \frac{{x + 1}}{{\left( {1 - x} \right)\left( {1 + x} \right)}} - \frac{{2{\rm{x}}}}{{\left( {1 - x} \right)\left( {1 + x} \right)}} = \frac{{x + 1 - 2{\rm{x}}}}{{\left( {1 - x} \right)\left( {1 + x} \right)}} = \frac{{1 - {\rm{x}}}}{{\left( {1 - x} \right)\left( {1 + x} \right)}} = \frac{1}{{x + 1}}\)
Vậy \(\frac{1}{{1 - x}} + \frac{{2{\rm{x}}}}{{{x^2} - 1}} = \frac{1}{{x + 1}}\).
Câu 47:
 Xem đáp án
Xem đáp án
Lời giải
Vì mức sản xuất của 3 tổ công nhân tỉ lệ với 5; 4; 3 nên ta gọi mức sản xuất của 3 tổ lần lượt là 5a; 4a; 3a ( với a ∈ ℕ và a > 0)
Tổ I tăng năng suất 10% , tổ II tăng năng suất 20%, tổ III tăng năng suất 10% nên mức sản xuất của 3 tổ là:
• Tổ I: 5a + 5a . 10 % = 5,5a;
• Tổ II: 4a + 4a . 20 % = 4,8a;
• Tổ III: 3a + 3a . 10% = 3,3a.
Trong cùng 1 thời gian, tổ I làm nhiều hơn tổ II 7 sản phẩm nên:
5,5a – 4,8a = 7
⇔ 0,7a = 7
⇔ a = 10
Số sản phẩm tổ I làm trong thời gian đó là: 10.5,5 = 55 (sản phẩm).
Số sản phẩm tổ II làm trong thời gian đó là: 10.4,8 = 48 (sản phẩm).
Số sản phẩm tổ III làm trong thời gian đó là: 10.3,3 = 33 (sản phẩm).
