Cho tam giác ABC. Gọi P, Q, R lần lượt là trung điểm của các cạnh BC, CA, AB.
a) Xác định điểm N thỏa mãn \(\overrightarrow {NA} + \overrightarrow {NB} + 2\overrightarrow {NC} = \overrightarrow 0 \).
b) Phân tích \(\overrightarrow {AM} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \) với M ∈ BC thỏa mãn \(\overrightarrow {BM} = \frac{2}{5}\overrightarrow {BC} \).
c) Với điểm O bất kì, chứng minh \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {ON} \).
Giải bởi Vietjack
Lời giải
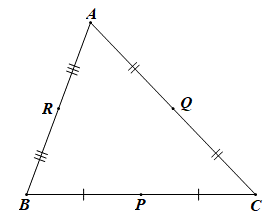
a) Do R là trung điểm của AB nên \(\overrightarrow {NA} + \overrightarrow {NB} = 2\overrightarrow {N{\rm{R}}} \)
Ta có \(\overrightarrow {NA} + \overrightarrow {NB} + 2\overrightarrow {NC} = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {NR} + 2\overrightarrow {NC} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {NR} + \overrightarrow {NC} = \overrightarrow 0 \)
Suy ra N là trung điểm của CR.
b) Ta có\(\overrightarrow {BM} = \frac{2}{5}\overrightarrow {BC} \)
\( \Leftrightarrow \overrightarrow {BA} + \overrightarrow {AM} = \frac{2}{5}\overrightarrow {BA} + \frac{2}{5}\overrightarrow {AC} \)
\( \Leftrightarrow \overrightarrow {AM} = \frac{2}{5}\overrightarrow {BA} + \frac{2}{5}\overrightarrow {AC} - \overrightarrow {BA} \)
\( \Leftrightarrow \overrightarrow {AM} = \frac{3}{5}\overrightarrow {AB} + \frac{2}{5}\overrightarrow {AC} \).
c) Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = \overrightarrow {ON} + \overrightarrow {NA} + \overrightarrow {ON} + \overrightarrow {NB} + 2\overrightarrow {ON} + 2\overrightarrow {NC} \)
\( = 4\overrightarrow {ON} + \overrightarrow {NA} + + \overrightarrow {NB} + 2\overrightarrow {NC} = 4\overrightarrow {ON} \) (vì \(\overrightarrow {NA} + \overrightarrow {NB} + 2\overrightarrow {NC} = \overrightarrow 0 \))
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {ON} \).
Cho tam giác ABC có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng bốn điểm A; D; H; E cùng nằm trên một đường tròn (gọi tâm của nó là O).
b) Gọi M là trung điểm của BC. Chứng minh ME là tiếp tuyến đường tròn (O).
Cho tam giác ABC cân tại A có các đường cao AH và BK cắt nhau tại I. Chứng minh:
a) Đường tròn đường kính AI đi qua K.
b) HK là tiếp tuyến của đường tròn đường kính AI.
Cho đường tròn tâm O bán kính R và một điểm M nằm ngoài đường tròn. Qua M kẻ tiếp tuyến MA với đường tròn (A là tiếp điểm). Tia Mx nằm giữa MA và MO cắt đường tròn (O; R) tại 2 điểm C và D (C nằm giữa M và D). Gọi I là trung điểm của dây CD, kẻ AH vuông góc với MO tại H.
a) Chứng minh OH . OM không đổi.
b) Chứng minh bốn điểm M, A, I, O cùng thuộc 1 đường tròn.
c) Gọi K là giao điểm của OI với HA. Chứng minh KC là tiếp tuyến của đường tròn (O; R).
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H lên AB, AC.
a) Chứng minh AD . AB = AE . AC.
b) Chứng minh \(\frac{{BH}}{{HC}} = {\left( {\frac{{AB}}{{AC}}} \right)^2}\).
c) Cho BH = 4 cm, CH = 9 cm. Tính DE và \(\widehat {A{\rm{D}}E}\) (làm tròn đến độ).
d) Gọi M là trung điểm của BH, N là trung điểm của CH. Tính SDENM.
Cho hàm số bậc nhất y = ax + 3.
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2; 6).
b) Vẽ đồ thị của hàm số với hệ số a tìm được ở câu a.
Cho đường tròn (O; R), đường kính AB. Vẽ dây AC sao cho \(\widehat {CAB} = 30^\circ \). Trên tia đối của tia BA, lấy điểm M sao cho BM = R. Chứng minh:
a) MC là tiếp tuyến của đường tròn (O).
b) MC2 = 3R2.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(– 4; 1); B(2; 4); C(2; –2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho.
Cho tam giác ABC nội tiếp đường tròn tâm O trực tâm H đường kính AD
a) Chứng minh \(\overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {H{\rm{D}}} \).
b) Gọi M là trung điểm BC. Chứng minh \(\overrightarrow {AH} = 2\overrightarrow {OM} \).
c) Gọi H' là điểm đối xứng với H qua O. Chứng minh \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HH'} \).
d) Gọi D' là điểm đối xứng với B qua O. Chứng minh \(\overrightarrow {AH} = \overrightarrow {D'C} \).
Cho 7 điểm A, B, C, D, E, F, G. Chứng minh
a) \(\overrightarrow {AB} + \overrightarrow {C{\rm{D}}} + \overrightarrow {EF} + \overrightarrow {GA} = \overrightarrow {CB} + \overrightarrow {E{\rm{D}}} + \overrightarrow {GF} \).
b) \(\overrightarrow {AB} - \overrightarrow {AF} + \overrightarrow {C{\rm{D}}} - \overrightarrow {CB} + \overrightarrow {EF} - \overrightarrow {E{\rm{D}}} = \overrightarrow 0 \).
Cho hàm số bậc nhất y = (m – 1)x + 2m – 5 (d1).
a) Tính giá trị của m để đường thẳng (d1) song song với đường thẳng y = 3x + 1 (d2).
b) Với giá trị nào của m thì đường thẳng (d1) và (d2) cắt nhau tại một điểm trên trục hoành.
Cho biểu thức:
\(A = \frac{{\sqrt x + 1}}{{\sqrt x - 2}} + \frac{2}{{\sqrt x + 3}} - \frac{{9\sqrt x - 3}}{{x + \sqrt x - 6}}\) và \(B = \frac{{x - \sqrt x + 1}}{{\sqrt x - 1}}\) với x ≥ 0, x ≠ 1, x ≠ 4.
a) Tính giá trị biểu thức B khi x = 9.
b) Rút gọn A.
c) Chứng minh rằng khi A > 0 thì B ≥ 3.
