Cho đường tròn tâm O bán kính R và một điểm M nằm ngoài đường tròn. Qua M kẻ tiếp tuyến MA với đường tròn (A là tiếp điểm). Tia Mx nằm giữa MA và MO cắt đường tròn (O; R) tại 2 điểm C và D (C nằm giữa M và D). Gọi I là trung điểm của dây CD, kẻ AH vuông góc với MO tại H.
a) Chứng minh OH . OM không đổi.
b) Chứng minh bốn điểm M, A, I, O cùng thuộc 1 đường tròn.
c) Gọi K là giao điểm của OI với HA. Chứng minh KC là tiếp tuyến của đường tròn (O; R).
Giải bởi Vietjack
Lời giải
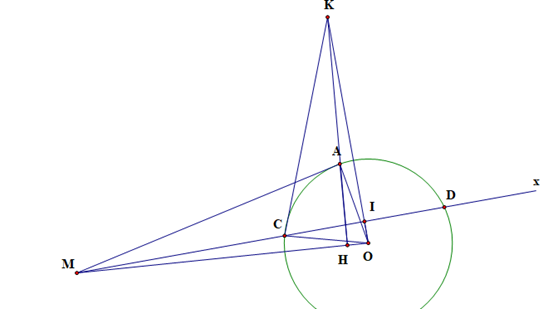
a) Vì MA là tiếp tuyến của (O) nên MA ⊥ OA
Xét tam giác AMO vuông tại A có AH ⊥ OM
Suy ra OH . OM = OA2 = R2
Vì R không đổi nên OH . OM không đổi.
b) Vì OC = OD nên ΔOCD cân tại O
Mà OI là đường trung tuyến, nên OI ⊥ CD
Xét tứ giác OIAM có
\(\widehat {OIM} = \widehat {OAM}\left( { = 90^\circ } \right)\)
Nên OIAM là tứ giác nội tiếp
Vậy bốn điểm M, A, I, O cùng thuộc 1 đường tròn.
c) Xét ΔOHK và ΔOIM có
\(\widehat {OHK} = \widehat {OIM}\left( { = 90^\circ } \right)\)
\(\widehat {HOK}\) là góc chung
Suy ra (g.g)
Do đó \(\frac{{OH}}{{OI}} = \frac{{OK}}{{OM}}\)
Suy ra OI . OK = OH . OM = R2 = OC2
Do đó \(\frac{{OC}}{{OK}} = \frac{{OI}}{{OC}}\)
Xét ΔOCK và ΔOIC có
\(\frac{{OC}}{{OK}} = \frac{{OI}}{{OC}}\)
\(\widehat O\) là góc chung
Suy ra (g.g)
Do đó \(\widehat {OCK} = \widehat {OIC} = 90^\circ \) (hai góc tương ứng)
Hay OC ⊥ OK
Suy ra KC là tiếp tuyến của (O).
Cho tam giác ABC có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng bốn điểm A; D; H; E cùng nằm trên một đường tròn (gọi tâm của nó là O).
b) Gọi M là trung điểm của BC. Chứng minh ME là tiếp tuyến đường tròn (O).
Cho tam giác ABC cân tại A có các đường cao AH và BK cắt nhau tại I. Chứng minh:
a) Đường tròn đường kính AI đi qua K.
b) HK là tiếp tuyến của đường tròn đường kính AI.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H lên AB, AC.
a) Chứng minh AD . AB = AE . AC.
b) Chứng minh \(\frac{{BH}}{{HC}} = {\left( {\frac{{AB}}{{AC}}} \right)^2}\).
c) Cho BH = 4 cm, CH = 9 cm. Tính DE và \(\widehat {A{\rm{D}}E}\) (làm tròn đến độ).
d) Gọi M là trung điểm của BH, N là trung điểm của CH. Tính SDENM.
Cho hàm số bậc nhất y = ax + 3.
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2; 6).
b) Vẽ đồ thị của hàm số với hệ số a tìm được ở câu a.
Cho đường tròn (O; R), đường kính AB. Vẽ dây AC sao cho \(\widehat {CAB} = 30^\circ \). Trên tia đối của tia BA, lấy điểm M sao cho BM = R. Chứng minh:
a) MC là tiếp tuyến của đường tròn (O).
b) MC2 = 3R2.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(– 4; 1); B(2; 4); C(2; –2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho.
Cho tam giác ABC nội tiếp đường tròn tâm O trực tâm H đường kính AD
a) Chứng minh \(\overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {H{\rm{D}}} \).
b) Gọi M là trung điểm BC. Chứng minh \(\overrightarrow {AH} = 2\overrightarrow {OM} \).
c) Gọi H' là điểm đối xứng với H qua O. Chứng minh \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HH'} \).
d) Gọi D' là điểm đối xứng với B qua O. Chứng minh \(\overrightarrow {AH} = \overrightarrow {D'C} \).
Cho 7 điểm A, B, C, D, E, F, G. Chứng minh
a) \(\overrightarrow {AB} + \overrightarrow {C{\rm{D}}} + \overrightarrow {EF} + \overrightarrow {GA} = \overrightarrow {CB} + \overrightarrow {E{\rm{D}}} + \overrightarrow {GF} \).
b) \(\overrightarrow {AB} - \overrightarrow {AF} + \overrightarrow {C{\rm{D}}} - \overrightarrow {CB} + \overrightarrow {EF} - \overrightarrow {E{\rm{D}}} = \overrightarrow 0 \).
Cho hàm số bậc nhất y = (m – 1)x + 2m – 5 (d1).
a) Tính giá trị của m để đường thẳng (d1) song song với đường thẳng y = 3x + 1 (d2).
b) Với giá trị nào của m thì đường thẳng (d1) và (d2) cắt nhau tại một điểm trên trục hoành.
Cho biểu thức:
\(A = \frac{{\sqrt x + 1}}{{\sqrt x - 2}} + \frac{2}{{\sqrt x + 3}} - \frac{{9\sqrt x - 3}}{{x + \sqrt x - 6}}\) và \(B = \frac{{x - \sqrt x + 1}}{{\sqrt x - 1}}\) với x ≥ 0, x ≠ 1, x ≠ 4.
a) Tính giá trị biểu thức B khi x = 9.
b) Rút gọn A.
c) Chứng minh rằng khi A > 0 thì B ≥ 3.
