- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 68)
-
12893 lượt thi
-
62 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Tìm số trung bình cộng của các số sau: 26,45; 45,12; 12,43.
 Xem đáp án
Xem đáp án
Trung bình cộng của các số:
(26,45 + 45,12 + 12,43) : 3 = 28.
Vậy trung bình cộng của các số trên là 28.
Câu 2:
Tìm số nguyên x, y biết: (3x – 1)(y + 4) = 13.
 Xem đáp án
Xem đáp án
Ta có:
(3x – 1)(y + 4) = 13
Suy ra 3x -1 ; y + 4 là các ước của 13.
\( \Rightarrow \) ( 3x – 1; y + 4) ∈ {(1; 13); (−1; −13); (13; 1); (−13; −1)}
\( \Rightarrow \) (x, y) ∈ \[\left\{ {\left( {\frac{2}{3};9} \right);\left( {\frac{{14}}{3}; - 3} \right);\left( {0; - 17} \right);\left( { - 4; - 5} \right)} \right\}\]
Mà x, y ∈ ℤ nên ta có: x, y ∈ {(0; −17); (−4; −5)}.
Câu 3:
Tìm số nguyên x, y biết: (5x – 1)(y + 1) = − 4.
 Xem đáp án
Xem đáp án
Ta có: (5x – 1)(y + 1) = −4
Suy ra 5x – 1; y + 1 là các ước của −4.
\( \Rightarrow \) ( 5x – 1; y + 1) ∈ {(1; −4); (−1; 4); (2; −2); (−2; 2); (4; −1); (−4; 1)}
\( \Rightarrow \) (x, y) ∈ \(\left\{ {\left( {\frac{2}{5}; - 5} \right);\left( {0;3} \right);\left( {\frac{3}{5}; - 3} \right);\left( {\frac{{ - 1}}{5};1} \right);\left( {1; - 2} \right);\left( {\frac{{ - 3}}{5};0} \right)} \right\}\).
Mà x, y ∈ ℤ nên ta có: x, y ∈ {(0; 3); (1; −2)}.
Câu 4:
Tính: (−|−7|).[(−2)4 + (−36) : (−3)2] – (−5)3.
 Xem đáp án
Xem đáp án
(−|−7|).[(−2)4 + (−36) : (−3)2] – (−5)3
= (−7).(16 – 36 : 9) + 53
= (−7).(16 – 4) + 125
= (−7).12 + 125
= 125 – 84 = 41.
Câu 5:
Tính bằng hai cách phép tính: 5 ´ 2 ´ 7.
 Xem đáp án
Xem đáp án
• Cách 1: 5 ´ 2 ´ 7 = (5 ´ 2) ´ 7 = 10 ´ 7 = 70;
• Cách 2: 5 ´ 2 ´ 7 = 5 ´ (2 ´ 7) = 5 ´ 14 = 70.
Câu 6:
Tìm x, biết:
a) 2(x – 5) – 3(x + 7) = 14;
b) 7(5 – x) – 2(x – 10) = 15.
 Xem đáp án
Xem đáp án
a) 2(x – 5) – 3(x + 7) = 14
2x – 2.5 – 3x – 3.7 = 14
−x – 10 – 21 = 14
−x – 31 = 14
x = −31 – 14
x = − 45
Vậy x = − 45.
b) −7(5 – x) – 2(x – 10) = 15
−7.5 + 7x – 2x + 20 = 15
−35 + 20 + 5x = 15
5x = 15 + 15
5x = 30
x = 6
Vậy x = 6.
Câu 7:
Tính nhanh: 234,56 ´ 55,4 + 234,56 ´ 44,6.
 Xem đáp án
Xem đáp án
234,56 ´ 55,4 + 234,56 ´ 44,6
= 234,56 ´ (55,4 + 44,6)
= 234,56 ´ 100 = 23 456.
Câu 8:
Tính bằng cách thuận tiện nhất:
a) 0,43 ´ 2 + 0,36 ´ 2 + 0,21 ´ 2;
b) 22,33 ´ 55,4 + 22,33 ´ 44,6.
 Xem đáp án
Xem đáp án
a) 0,43 ´ 2 + 0,36 ´ 2 + 0,21 ´ 2
= 2 ´ (0,43 + 0,36 + 0,21)
= 2 ´ 1 = 2.
b) 22,33 ´ 55,4 + 22,33 ´ 44,6.
= 22,33 ´ (55,4 + 44,6)
= 22,33 ´ 100 = 2233.
Câu 9:
Phân tích đa thức thành nhân tử: x2 + xy – 5x – 5y.
 Xem đáp án
Xem đáp án
x2 + xy – 5x – 5y
= (x2 + xy) – (5x + 5y)
= x(x + y) – 5(x + y)
= (x + y)(x – 5).
Câu 10:
Tìm x, y biết \[\frac{x}{y} = \frac{2}{5}\] và xy = 40.
 Xem đáp án
Xem đáp án
Ta có: \(\frac{x}{y} = \frac{2}{5} \Rightarrow \frac{x}{2} = \frac{y}{5}\)
Đặt \(\frac{x}{2} = \frac{y}{5} = k\)
\( \Rightarrow \left\{ \begin{array}{l}x = 2k\\y = 5k\end{array} \right.\)
Khi đó ta có: xy = 40
\( \Rightarrow \) 2k.5k = 40
\( \Leftrightarrow \) 10k2 = 40
\( \Leftrightarrow \) k2 = 4
\( \Leftrightarrow \) k = ± 2
+) Với k = 2
\( \Rightarrow \) x = 2.2 = 4; y = 5.2 = 10
+) Với k = −2
\( \Rightarrow \) x = 2.(−2) = −4; y = 5.(−2) = −10
Vậy (x; y) = (4; 10) hoặc (x; y) = (−4; −10)
Câu 11:
Tìm x, biết: \(2\sqrt x + \sqrt {3x + 2} = 2 + \sqrt {x + 4} \).
 Xem đáp án
Xem đáp án
Điều kiện xác định: \(\left\{ \begin{array}{l}x \ge 0\\3x + 2 \ge 0\\x + 4 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ge \frac{{ - 2}}{3}\\x \ge - 4\end{array} \right. \Leftrightarrow x \ge 0\)
\(2\sqrt x + \sqrt {3x + 2} = 2 + \sqrt {x + 4} \)
\( \Leftrightarrow 2\left( {\sqrt x - 1} \right) + \left( {\sqrt {3x + 2} - \sqrt {x + 4} } \right) = 0\)
\( \Leftrightarrow \frac{{2\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)}} + \frac{{\left( {\sqrt {3x + 2} - \sqrt {x + 4} } \right)\left( {\sqrt {3x + 2} + \sqrt {x + 4} } \right)}}{{\left( {\sqrt {3x + 2} + \sqrt {x + 4} } \right)}} = 0\)
\( \Leftrightarrow \frac{{2\left( {x - 1} \right)}}{{\sqrt x + 1}} + \frac{{(3x + 2) - (x + 4)}}{{\sqrt {3x + 2} + \sqrt {x + 4} }} = 0\)
\( \Leftrightarrow \frac{{2(x - 1)}}{{\sqrt x + 1}} + \frac{{2(x - 1)}}{{\sqrt {3x + 2} + \sqrt {x + 4} }} = 0\)
\( \Leftrightarrow 2(x - 1)\left( {\frac{1}{{\sqrt x + 1}} + \frac{1}{{\sqrt {3x + 2} + \sqrt {x + 4} }}} \right) = 0\) (*)
Với x ≥ 0 ta có:
\(\frac{1}{{\sqrt x + 1}} + \frac{1}{{\sqrt {3x + 2} + \sqrt {x + 4} }} > 0\)
Khi đó (*) \( \Leftrightarrow \) x – 1 = 0
\( \Leftrightarrow \) x = 1 (thỏa mãn điều kiện)
Vậy phương trình đã cho có nghiệm duy nhất x = 1.
Câu 12:
Cho biểu thức: \(A = \left( {\frac{{x + 2\sqrt x }}{{x - 2\sqrt x }} + \frac{{\sqrt x }}{{\sqrt x - 2}}} \right).\frac{1}{{\sqrt x + 1}}\) (với x > 0; x ≠ 4).
Rút gọn biểu thức A.
 Xem đáp án
Xem đáp án
\(A = \left( {\frac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\sqrt x \left( {\sqrt x - 2} \right)}} + \frac{{\sqrt x }}{{\sqrt x - 2}}} \right).\frac{1}{{\sqrt x + 1}}\)
\( = \left( {\frac{{\sqrt x + 2}}{{\sqrt x - 2}} + \frac{{\sqrt x }}{{\sqrt x - 2}}} \right).\frac{1}{{\sqrt x + 1}}\)
\( = \frac{{\sqrt x + 2 + \sqrt x }}{{\sqrt x - 2}}.\frac{1}{{\sqrt x + 1}}\)
\( = \frac{{2\sqrt x + 2}}{{\sqrt x - 2}}.\frac{1}{{\sqrt x + 1}} = \frac{{2\left( {\sqrt x + 1} \right)}}{{\sqrt x - 2}}.\frac{1}{{\sqrt x + 1}}\)
\( = \frac{2}{{\sqrt x - 2}}\)
Vậy \(A = \frac{2}{{\sqrt x - 2}}\).
Câu 13:
Khai triển: (a + b + c)2; (a + b – c)2.
 Xem đáp án
Xem đáp án
• (a + b + c)2 = [(a + b) + c]2
= (a + b)2 + 2(a + b).c + c2
= a2 + 2ab + b2 + 2ac + 2bc + c2
= a2 + b2 + c2 + 2ab + 2ac + 2bc
• (a + b – c)2 = [(a + b) – c]2
= (a + b)2 – 2(a + b)c + c2
= a2 + b2 + 2ab – 2ac – 2bc + c2
= a2 + b2 + c2 + 2ab – 2ac – 2bc
Câu 14:
Phân tích đa thức thành nhân tử:
a(b + c)2(b – c) + b(c + a)2(c – a) + c(a + b)2(a – b).
 Xem đáp án
Xem đáp án
a(b + c)2(b – c) + b(c + a)2(c – a) + c(a + b)2(a – b)
= a(b + c)2(b – c) – b(c + a)2(b – c – b + a) + c(a + b)2(a – b)
= a(b + c)2(b – c) – b(c + a)2(b – c) – b(c + a)2(a – b) + c(a + b)2(a – b)
= (b – c)[a(b + c)2 – b(c + a)2] – (a – b)[b(c + a)2 – c(a + b)2]
= (b – c)(ab2 + ac2 + 2abc – bc2 – ba2 – 2abc) – (a – b)(bc2 + ba2 + 2abc – ca2 – cb2 – 2abc)
= (b – c)(ab2 + ac2 – bc2 – ba2) – (a – b)(bc2 + ba2 – ca2 – cb2)
= (b – c)[ab(b – a) + c2(a – b)] – (a – b)[bc(c – b) + a2(b – c)]
= (b – c)(a – b)(c2 – ab) – (a – b)(b – c)(a2 – bc)
= (a – b)(b – c)(c2 – ab – a2 + bc)
= (a – b)(b – c)[(c – a)(c + a) + b(c – a)]
= (a – b)(b – c)(c – a)(a + b + c).
Câu 15:
Ba công nhân dược thưởng 100 000 đồng, số tiền thưởng được phân chia tỉ lệ với mức sản xuất của mỗi người. Biết mức sản xuất của người thứ nhất so với mức sản xuất của người thứ hai bằng 5 : 3, mức sản xuất của người thứ ba bằng 25% tổng số mức sản xuất của hai người kia. Tính số tiền mỗi người được thưởng.
 Xem đáp án
Xem đáp án
Tổng số phần của mức sản xuất của người thứ 1 và thứ 2 là:
5 + 3 = 8 (phần)
Người thứ 3 bằng 25% tổng của người thứ nhất và người thứ 2 nên chiếm số phần là:
\(8.\frac{{25}}{{100}} = 2\) (phần)
Ta có sơ đồ sau:

Theo sơ đồ, tổng mức sản xuất của ba người là:
5 + 3 + 2 = 10 (phần)
Số tiền của người thứ nhất được thưởng là:
\(\frac{{100\,\,000.5}}{{10}} = 50\,\,000\)(đồng)
Số tiền của người thứ 2 được thưởng là:
\(100\,\,000\,\,.\,\,\frac{3}{{10}} = 30\,\,000\) (đồng)
Số tiền của người thứ 3 được thưởng là:
100 000 – 50 000 – 30 000 = 20 000 (đồng)
Vậy số tiền của người thứ nhất được thưởng là: 50 000 đồng.
Số tiền của người thứ 2 được thưởng là: 30 000 đồng.
Số tiền của người thứ 3 được thưởng là: 20 000 đồng.
Câu 16:
Ba tổ công nhân có mức sản xuất tỉ lệ với 5; 4; 3. Tổ I tăng năng suất 10%, tổ II tăng năng suất 20%, tổ III tăng năng suất 10%. Do đó trong cùng một thời gian, tổ I làm được nhiều sản phầm hơn tổ II là 7 sản phẩm. Tính số sản phẩm mỗi tổ làm được trong thời gian đó khi chưa tăng năng suất làm việc.
 Xem đáp án
Xem đáp án
Mức sản xuất của mỗi tổ tỉ lệ 5: 4 : 3 cũng có nghĩa là số sản phẫm cũng có tỉ lệ là
5 : 4 : 3
Gọi số sản phẫm mà 3 tổ công nhân làm được lần lượt là 5x, 4x, 3x (x > 0)
Khi đó số sản phẩm mà tổ I làm được khi tăng năng suất 10% là:
5x.110% = 5,5x (sản phẩm)
Số sản phẩm mà tổ II làm được khi tăng năng suất 20% là:
4x.120% = 4,8x (sản phẩm)
Số sản phẩm mà tổ III làm được khi tăng năng suất 10% là:
3x.110% = 3,3x (sản phẩm)
Do khi tăng năng suất thì tổ I làm nhiều hơn tổ II 7 sản phẩm nên ta có phương trình:
5,5x – 4,8x = 7
\( \Leftrightarrow \) 0,7x = 7
\( \Leftrightarrow \) x = 10
Vậy tổ I làm được số sản phẩm là: 5. 10 = 50 (sản phẩm)
Tổ II làm được số sản phẩm là: 4. 10 = 40 (sản phẩm)
Tổ III làm được số sản phẩm là: 3. 10 = 30 (sản phẩm)
Đáp số: Tổ I làm được 50 sản phẩm.
Tổ II làm được 40 sản phẩm.
Tổ III làm được 30 sản phẩm.
Câu 17:
Ba tổ công nhân có mức sản xuất tỉ lệ với 5; 4; 3. Tổ I tăng năng suất 10%, tổ II tăng năng suất 20%, tổ III tăng năng suất 30%. Do đó trong cùng một thời gian, tổ I làm được nhiều sản phầm hơn tổ III là 16 sản phẩm. Tính tổng số sản phẩm của ba tổ làm được là bao nhiêu khi họ chưa tăng năng suất làm việc?
 Xem đáp án
Xem đáp án
Mức sản xuất của mỗi tổ tỉ lệ 5: 4 : 3 cũng có nghĩa là số sản phẫm cũng có tỉ lệ là
5 : 4 : 3
Gọi số sản phẫm mà 3 tổ công nhân làm được lần lượt là 5x, 4x, 3x (x > 0)
Khi đó số sản phẩm mà tổ I làm được khi tăng năng suất 10% là:
5x.110% = 5,5x (sản phẩm)
Số sản phẩm mà tổ II làm được khi tăng năng suất 20% là:
4x.120% = 4,8x (sản phẩm)
Số sản phẩm mà tổ III làm được khi tăng năng suất 30% là:
3x.110% = 3,9x (sản phẩm)
Do khi tăng năng suất thì tổ I làm nhiều hơn tổ III 16 sản phẩm nên ta có phương trình:
5,5x – 3,9x = 16
\( \Leftrightarrow \) 1,6x = 16
\( \Leftrightarrow \) x = 10
Vậy tổng số sản phẩm mà 3 tổ làm được nếu không tăng năng suất là: 50 + 40 + 30 = 120 (sản phẩm)
Đáp số: 120 sản phẩm.
Câu 18:
Chứng mình rằng với n ∈ ℕ* thì
\(1 + 2 + 3 + ... + n = \frac{{n\left( {n + 1} \right)}}{2}\).
 Xem đáp án
Xem đáp án
Khi n = 1, VT = 1
\(VP = \frac{{1\left( {1 + 1} \right)}}{2} = 1\)
\( \Rightarrow \) VT = VP, do đó đẳng thức đúng với n = 1.
Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là:
Sk = 1 + 2 + 3 + … + k = \(\frac{{k\left( {k + 1} \right)}}{2}\)
Ta phải chứng mình rằng đẳng thức cũng đúng với n = k + 1, tức là:
Sk+1 = 1 + 2 + 3 + … + k + (k + 1) = \(\frac{{\left( {k + 1} \right)(k + 2)}}{2}\)
Thật vậy, từ giả thuyết suy ra ta có:
Sk+1 = Sk + (k + 1) = \(\frac{{k\left( {k + 1} \right) + 2\left( {k + 1} \right)}}{2} = \frac{{(k + 1)(k + 2)}}{2}\)
Suy ra đẳng thức đúng với mọi n ∈ ℕ*.
Câu 19:
Có 4 bao tải gạo, bao thứ hai nặng gấp đôi bao thứ nhất, bao thứ ba nặng hơn bao thứ hai 12,5 kg, bao thứ tư ít hơn bao thứ ba 6,3kg. Biết rằng cả 4 bao có tất cả 53,7kg gạo. Hỏi bao thứ ba có bao nhiêu kg gạo?
 Xem đáp án
Xem đáp án
Theo bài cho ta có:
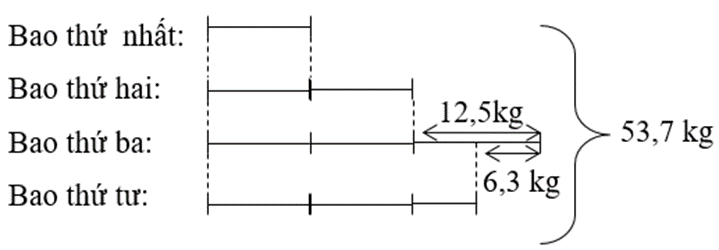
Bao thứ 4 có nhiều hơn bao thứ 2 là:
12,5 – 6,3 = 6,2 (kg)
7 lần bao thứ nhất là:
53,7 – 12, 5 – 6,2 = 35 (kg)
Bao thứ nhất nặng:
35 : 7 = 5 (kg)
Bao thứ ba nặng:
5 ´ 2 + 12,5 = 22,5 (kg)
Đáp số: 22,5 kg gạo
Câu 20:
Có 24 cái cốc được xếp đều vào 4 hộp. Hỏi mỗi hộp có bao nhiêu cái?
 Xem đáp án
Xem đáp án
Số cốc trong mỗi hộp là:
24 : 4 = 6 (cốc)
Đáp số: 6 cái cốc
Câu 21:
Cứ 10 học sinh thì phân đều vào 5 bàn học. Hỏi có 36 học sinh cũng phân như thế thì cần bao nhiêu bàn học?
 Xem đáp án
Xem đáp án
Số học sinh có trong mỗi bàn là:
10 : 5 = 2 (học sinh)
Với 36 học sinh thì cần số bàn học là:
36 : 2 = 18 (bàn)
Đáp số: 18 bàn
Câu 22:
Trong các tam giác vuông có độ dài các cạnh là số nguyên mà giá trị diện tích và chu vi bằng nhau, độ dài đường cao ứng với cạnh huyền đạt giá trị lớn nhất có thể là?
 Xem đáp án
Xem đáp án
Gọi độ dài hai cạnh góc vuông là a và b (a,b ∈ ℕ*, đvđd)
\( \Rightarrow \) Độ dài cạnh huyền là \[\sqrt {{a^2} + {b^2}} \].
Gọi đường cao là h.
Khi đó:
Chu vi của tam giác là: \(a + b + \sqrt {{a^2} + {b^2}} \)
Diện tích của tam giác là: \(\frac{1}{2}.\sqrt {{a^2} + {b^2}} .h\)
Theo bài ra ta có:
\(a + b + \sqrt {{a^2} + {b^2}} = \frac{1}{2}\sqrt {{a^2} + {b^2}} .h\)
\( \Rightarrow h = \frac{{2a + 2b + 2\sqrt {{a^2} + {b^2}} }}{{\sqrt {{a^2} + {b^2}} }} = 2 + 2\frac{{a + b}}{{\sqrt {{a^2} + {b^2}} }}\)
Theo bđt bunhiacopxki, ta có:
(1.a + 1.b)2 ≤ (12 + 12)(a2 + b2)
\( \Leftrightarrow a + b \le \sqrt {2\left( {{a^2} + {b^2}} \right)} \)
\( \Rightarrow h \le 2 + 2.\frac{{\sqrt {2\left( {{a^2} + {b^2}} \right)} }}{{\sqrt {{a^2} + {b^2}} }} = 2 + 2\sqrt 2 \).
Vậy \({h_{\max }} = 2 + 2\sqrt 2 \) (đvđd).
Câu 23:
Lớp 4A có 32 học sinh được chia đều vào 4 tổ. Hỏi:
a) 3 tổ chiếm mấy phần số học sinh của lớp?
b) 3 tổ có bao nhiêu học sinh?
 Xem đáp án
Xem đáp án
a) 3 tổ chiếm số phần của số học sinh của lớp là: \(\frac{3}{4}\).
b) 3 tổ có số học sinh là:
\(32.\frac{3}{4} = 24\) (học sinh)
Đáp số: a) \(\frac{3}{4}\);
b) 24 học sinh.
Câu 24:
Lớp 4A có 32 học sinh. Hôm nay có 3 bạn nữ nghỉ học nên số nam nhiều hơn số nữ là 5 bạn. Hỏi lớp 4A có bao nhiêu học sinh nữ,bao nhiêu học sinh nam?
 Xem đáp án
Xem đáp án
Nếu có 3 bạn nữ nghỉ ốm, lớp 4A còn lại số học sinh là:
32 – 3 = 29 (học sinh)
Số học sinh nam là: (29 + 5) : 2 = 17 (học sinh)
Số học sinh nữ là: 32 – 17 = 15 (học sinh)
Đáp số: Nam: 17 học sinh ;
Nữ: 15 học sinh.
Câu 25:
M có phải là số chính phương không nếu:
M = 1 + 3 + 5 + … + (2n – 1) Với n ∈ ℕ; n ≠ 0.
 Xem đáp án
Xem đáp án
M là tổng của số lẻ tự nhiên liên tiếp từ 1 đến (2n – 1).
Khi đó, tổng số các số hạng của M là:
(2n – 1 + 1) : 2 = n (số hạng)
Do đó M = (2n – 1 + 1) . n : 2 = 2n . n : 2 = n2
Suy ra M chính là một số chính phương.
Câu 26:
Một mảnh vườn hình chữ nhật được chia thành hai phần là hai hình vuông bằng nhau có cạnh 4 m. Tính chu vi mảnh vườn hình chữ nhật.
 Xem đáp án
Xem đáp án
Chiều dài của mảnh vườn đó là:
4 + 4 = 8 ( m )
Chu vi của mảnh vườn đó là:
(8 + 4) ´ 2 = 24 (m)
Đáp số: 24 m
Câu 27:
Một mảnh vườn hình chữ nhật được chia làm 2 phần để trồng hành và trồng cà rốt. Trong đó diện tích trồng cà rốt gấp 5 lần diện tích trồng hành, chu vi đất trồng cà rốt lớn hơn chu vi đất trồng hành 936 m. Biết chiều rộng mảnh vườn ban đầu là 327 m. Hỏi chu vi mảnh ruộng ban đầu là bao nhiêu dam?
 Xem đáp án
Xem đáp án
Vì diện tích trồng cà rốt gấp 5 lần diên tích trồng hành nên cạnh còn lại của diện tích trồng cà rốt gấp 5 lần cạnh còn lại của phần trồng hành
Cạnh còn lại của diện tích trồng hành là:
936 : 2 : (5 – 1) × 1 = 117 (m)
Cạnh còn lại của diện tích trồng cà rốt là:
117 × 5 = 585 (m)
Chiều dài của mảnh đất ban đầu là:
117 + 585 = 702 (m)
Chu vi mảnh ruộng ban đầu là
(702 + 327) × 2 = 2058 (m) = 205,8 (dam)
Vậy chu vi mảnh ruộng ban đầu là 205,8 dam.
Câu 28:
Phân tích đa thức thành nhân tử: P = 2a3 + 7a2b + 7ab2 + 2b3.
 Xem đáp án
Xem đáp án
P = 2a3 + 7a2b + 7ab2 + 2b3
= 2(a3 + b3) + 7ab(a + b)
= 2(a + b)(a2 – ab + b2) + 7ab(a + b)
= (a + b)(2a2 – 2ab2 + 2b2 + 7ab)
= (a + b)(2a2 + 5ab + 2b2)
= (a + b)(2a2 + 4ab + ab + 2b2)
= (a + b)[2a(a + 2b) + b(a + 2b)]
= (a + b)(a + 2b)(2a + b).
Câu 29:
Tìm số dư của phép chia 235 : 17,2 nếu thương chỉ lấy đến hai chữ số ở phần thập phân
 Xem đáp án
Xem đáp án
Đáp án đúng là: D.
Ta có:

Vậy đáp án đúng là D.
Câu 30:
Nếu thương chỉ lấy đến hai chữ số ở thập phân thì dư của các phép chia sau là bao nhiêu:
a) 25 : 52;
b) 48 : 23.
 Xem đáp án
Xem đáp án
a) Ta có:

Vậy phép chia có thương là 0,48 (dư 0,04)
b) Ta có:
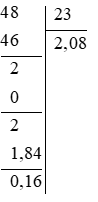
Vậy phép chia có thương là 2,08 (dư 0,16)
Câu 31:
Tìm n ∈ ℤ để 2n2 + 3n + 3 \( \vdots \) 2n – 1.
 Xem đáp án
Xem đáp án
Ta có:
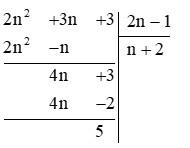
5 \( \vdots \) (2n – 1)
\( \Rightarrow \) (2n – 1) ∈ Ư(5) = {1; −1; 5; −5}
+) 2n – 1 = 1
n = 1
+) 2n – 1 = −1
n = 0
+) 2n – 1 = 5
n = 3
+) 2n – 1 = −5
n = −2
Vậy với x ∈ {−2; 0; 1; 3} thì thỏa mãn yêu cầu bài toán.
Câu 32:
Tìm x, biết:
a) 1,6x + 0,4x = 7;
b) 7,2x – 1,2x = 3.
 Xem đáp án
Xem đáp án
a) 1,6x + 0,4x = 7
(1,6 + 0,4)x = 7
2x = 7
x = 7 : 2
x = 3,5
Vậy x = 3,5.
b) 7,2x – 1,2x = 3
(7,2 – 1,2)x = 3
6x = 3
x = 2
Vậy x = 2.
Câu 33:
 Xem đáp án
Xem đáp án
Số có 4 chữ số thỏa yêu cầu có dạng:
• a có 4 cách chọn.
• b có 4 cách chọn.
• c có 4 cách chọn.
• d có 4 cách chọn.
Vậy theo quy tắc nhân có 4 . 4 . 4 . 4 = 256 (cách chọn).
Vậy ta có thể lập được 256 số.
Câu 34:
Từ các chữ số 1; 5; 6; 7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số khác nhau?
 Xem đáp án
Xem đáp án
Số có 4 chữ số thỏa yêu cầu có dạng:
a có 4 cách chọn.
b có 3 cách chọn.
c có 2 cách chọn.
d có 1 cách chọn.
Vậy theo quy tắc nhân có 4.3.2.1 = 24 cách chọn.
Vậy ta có thể lập được 24 số.
Câu 35:
Tìm x, biết: \(30\% x + \frac{1}{4}x + 89 = 100\).
 Xem đáp án
Xem đáp án
\(30\% x + \frac{1}{4}x + 89 = 100\)
\(\left( {\frac{3}{{10}} + \frac{1}{4}} \right)x + 89 = 100\)
\(\frac{{11}}{{20}}x = 100 - 89\)
\(\frac{{11}}{{20}}x = 11\)
x = 20
Vậy x = 20.
Câu 36:
Tìm ước của 200.
 Xem đáp án
Xem đáp án
Ta có: 200 = 2.2.2.5.5 = 23.52.
Vậy Ư(200) = {1; 2; 4; 5; 8; 10; 20; 25; 40; 50; 100; 200}.
Câu 37:
Tổng của hai số là 10,47. Nếu số hạng thứ nhất gấp 5 lần, số hạng thứ hai gấp lên 3 lần thì tổng hai số là 44,59. Tìm hai số đó?
 Xem đáp án
Xem đáp án
3 lần tổng hai số là: 10,47 ´ 3 = 31,41
2 lần số hạng thứ nhất là:
44,59 – 31,41 = 13,18
Vậy số hạng thứ nhát là:
13,18 : 2 = 6,59
Sô hạng thứ hai là:
10,47 – 6,59 = 3,88
Đáp số: Số thứ nhất là: 6,59;
Số thứ hai là: 3,88.
Câu 38:
Một ô tô trong 3 giờ đầu, mỗi giờ đi được 42,8 km. Hai giờ sau, mỗi giờ ô tô đi được 48,3 km. Hỏi trung bình mỗi giờ ô tô đó đi được bao nhiêu km?
 Xem đáp án
Xem đáp án
Trong 3 giờ đầu ô tô đi được số km là:
42,8 ´ 3 = 128,4 (km)
Trong 2 giờ sau ô tô đi được số km là:
48,3 ´ 2 = 96,6 (km)
Trung bình 1 giờ ô tô đi được số km là:
(128,4 + 96,6) : (3 + 2) = 45 (km)
Đáp số: 45 km.
Câu 39:
Một ô tô trong 3 giờ đầu, mỗi giờ đi được 42,5 km và trong 2 giờ sau, mỗi giờ đi được 43,25 km. Hỏi quãng đường ô tô đã đi trong 5 giờ là bao nhiêu?
 Xem đáp án
Xem đáp án
Tổng quãng đường ô tô đi được trong 5 giờ là:
42,5 ´ 3 + 43,25 ´ 2 = 214 (km)
Đáp số: 214 km.
Câu 40:
Tính nhanh: 123,45 ´ 55,4 + 123,45 ´ 54,6 – 1234,5.
 Xem đáp án
Xem đáp án
123,45 ´ 55,4 + 123,45 ´ 54,6 – 1234,5
= 123,45 ´ 55,4 + 123,45 ´ 54,6 – 123,45 ´ 10
= 123,45 ´ (55,4 + 54,6 – 10)
= 123,45 ´ 100 = 12 345.
Câu 41:
Tính nhanh: 512 ´ (2 – 128) – 128 ´ (−512).
 Xem đáp án
Xem đáp án
512 ´ (2 – 128) – 128 ´ (−512)
= 512 ´ (−126) + 128 ´ 512
= 512 ´ ( 128 – 126)
= 512 ´ 2 = 1024
Câu 42:
Tính:
a) \(\overline {ab} + \overline {ba} \), biết a + b = 15;
b) \(\overline {ab} - \overline {ba} \), biết a – b = 4.
 Xem đáp án
Xem đáp án
Ta có: \(\overline {ab} + \overline {ba} \)
= 10.a + b + 10.b + a
= 11(a + b)
= 11 ´ 15 = 165
Vậy \(\overline {ab} + \overline {ba} = 165\).
b) Ta có: \(\overline {ab} - \overline {ba} \)
= 10a + b – (10b + a)
= 9a – 9b
= 9(a – b)
= 9 ´ 4 = 36
Vậy \(\overline {ab} - \overline {ba} = 36\).
Câu 43:
Biết rằng 15 công nhân sửa xong 1 đoạn đường phải hết 6 ngày. Hỏi muốn sửa xong đoạn đường đó trong 3 ngày thì cần bổ sung bao nhiêu công nhân nữa?
 Xem đáp án
Xem đáp án
Một công nhân sẽ sửa trong đoạn đường đó trong số ngày là:
15 ´ 6 = 90 (ngày)
Nếu muốn sửa xong đoạn đường đó thì cần số công nhân là:
90 : 3 = 30 (người)
Vậy cần thêm số công nhân là:
30 – 15 = 15 (người)
Đáp số: 15 người.
Câu 44:
Biết số học sinh trường từ 700 đến 800 học sinh khi xếp hàng 30; 36; 40 đều thiếu 10 học sinh . Tính số học sinh trường đó.
 Xem đáp án
Xem đáp án
Gọi a là số học sinh của trường trên. (700 ≤ a ≤ 800, a ∈ ℕ).
Theo bài cho ta có:
(a + 10) chia hết cho 30; 40; 48 nên (a + 10) ∈ BC(30, 40, 48)
Ta có: 30 = 2 . 3 . 5; 40 = 23 . 5; 48 = 24 . 3.
Suy ra BCNN(30, 40, 48) = 24 . 3 . 5 = 240
Do đó a + 10 ∈ B(240) = {240; 480; 720; 960; …}
\( \Rightarrow \) a ∈ {230; 470; 710; 950; …}
Mà 700 ≤ a ≤ 800 nên a = 710.
Đáp số: 710 học sinh
Câu 45:
 Xem đáp án
Xem đáp án
\(A = \frac{a}{{ab + a + 2}} + \frac{b}{{bc + b + 1}} + \frac{{2c}}{{ac + 2c + 2}}\)
\( = \frac{a}{{ab + a + 2}} + \frac{{ab}}{{a\left( {bc + b + 1} \right)}} + \frac{{2abc}}{{ab\left( {ac + 2c + 2} \right)}}\)
\( = \frac{a}{{ab + a + 2}} + \frac{{ab}}{{abc + ab + a}} + \frac{{2abc}}{{{a^2}bc + 2abc + 2ab}}\)
Mà abc = 2 nên \(A = \frac{a}{{ab + a + 2}} + \frac{{ab}}{{2 + ab + a}} + \frac{{2.2}}{{a.2 + 2.2 + 2a}}\)
\( = \frac{{a + ab + 2}}{{ab + a + 2}}\)= 1.
Câu 46:
Rút gọn biểu thức sau: \(\frac{{{a^{\frac{1}{3}}}\sqrt b + {b^{\frac{1}{3}}}\sqrt a }}{{\sqrt[6]{a} + \sqrt[6]{b}}}\).
 Xem đáp án
Xem đáp án
\(\frac{{{a^{\frac{1}{3}}}\sqrt b + {b^{\frac{1}{3}}}\sqrt a }}{{\sqrt[6]{a} + \sqrt[6]{b}}}\)\( = \frac{{{a^{\frac{1}{3}}}\,.\,{b^{\frac{1}{2}}} + {b^{\frac{1}{3}}}\,.\,{a^{\frac{1}{2}}}}}{{{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}}}\)
\( = \frac{{{a^{\frac{1}{3}}}\,.\,{b^{\frac{1}{3} + \frac{1}{6}}} + {b^{\frac{1}{3}}}\,.\,{a^{\frac{1}{3} + \frac{1}{6}}}}}{{{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}}} = \frac{{{a^{\frac{1}{3}}}\,.\,{b^{\frac{1}{3}}}\,.\,{b^{\frac{1}{6}}} + {b^{\frac{1}{3}}}\,.\,{a^{\frac{1}{3}}}\,.\,\,{a^{\frac{1}{6}}}}}{{{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}}}\)
\( = \frac{{{a^{\frac{1}{3}}}\,.\,{b^{\frac{1}{3}}}\,.\,\left( {{b^{\frac{1}{6}}} + {a^{\frac{1}{6}}}} \right)}}{{{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}}} = {a^{\frac{1}{3}}}\,.\,{b^{\frac{1}{3}}} = \sqrt[3]{{ab}}\).
Câu 47:
Cho biết 3 người làm cỏ một mảnh vườn hết 8 giờ. Hỏi 12 người (với năng xuất làm việc như thế) làm cỏ mảnh vườn đó hết bao nhiêu thời gian?
 Xem đáp án
Xem đáp án
Một người làm thì làm cỏ mảnh vườn đó xong trong số giờ là:
3 ´ 8 = 24 (giờ)
Vậy 12 giờ làm cỏ mảnh vườn đó xong trong số giờ là:
24 : 12 = 2 (giờ)
Đáp số: 2 giờ.
Câu 48:
Cho hàm số y = (k – 3)x + k’ (d).
Tìm giá trị của k, k’ sao cho (d) cắt 2 điểm A(1; 2) và B(−3; 4).
 Xem đáp án
Xem đáp án
Vì (d) đi qua A(1; 2) và B(−3; 4) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}k - 3 + k' = 2\\ - 3k + 9 + k' = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = 2,5\\k' = 2,5\end{array} \right.\)
Vậy y = (2,5 – 3)x + 2,5 = −0,5x + 2,5.
Câu 49:
Cho tam giác ABC có AB = AC.Trên hai cạnh AB và AC lần lượt lấy 2 điểm M và N sao cho AM = AN. Gọi D, E làm lượt là trung điểm của MN và BC.
Chứng minh ba điểm A, E, D thẳng hàng.
 Xem đáp án
Xem đáp án
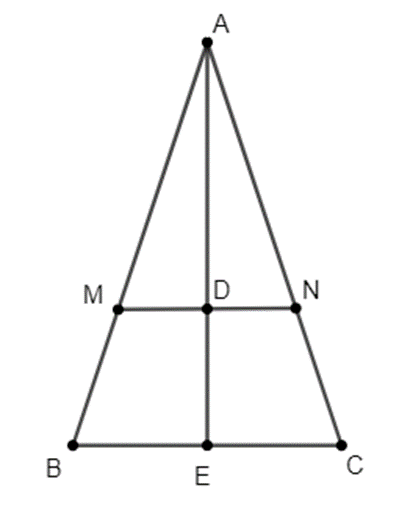
Xét ∆AMN có AM = AN nên ∆AMN cân tại A.
Vậy thì trung tuyến AD chính là phân giác của góc \(\widehat {MAN}\)
Xét ∆ABC có AB = AC nên ∆ABC cân tại A.
Vậy thì trung tuyến AE chính là phân giác của góc \(\widehat {BAC}\).
Từ đó ta có D, E cùng thuộc tia phân giác của góc A hay A, D, E thẳng hàng.
Câu 50:
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ đường kính CD. Tia phân giác của \(\widehat {BOD}\) cắt AB tại E.
a) Chứng minh rằng ED là tiếp tuyến của đường tròn (O).
b) Chứng minh AC + DE ≥ 2R.
c) Tính số đo \(\widehat {AOE}\).
 Xem đáp án
Xem đáp án
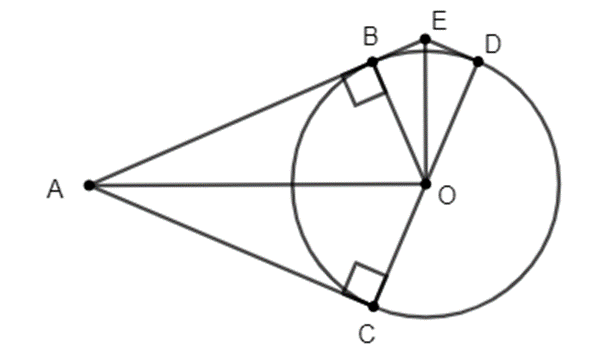
a) Xét ∆OBE và ∆ODE có:
OE là cạnh chung
\(\widehat {BOE} = \widehat {DOE}\) (gt)
OB = OD = R
Do đó ∆OBE = ∆ODE (c.g.c)
Suy ra \(\widehat {OBE} = \widehat {ODE} = 90^\circ \)
Do đó ED là tiếp tuyến của đường tròn (O).
b) Theo tính chất của hai tiếp tuyến cắt hau, ta có:
AC = AB; BE = DE
Nên: AC + DE = AB + BE = AE (1)
Từ câu a) ta có CD\( \bot \)DE, mà CD\( \bot \)AC (gt) nên ED // AC.
Vì CD là khoảng cách giữa hai đường thẳng song song AC và DE
nên AE ≥ CD = 2R (2)
Từ (1) và (2) suy ra: AC + DE ≥ 2R.
c) Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
OA là tia phân giác của \(\widehat {BOC}\), OE là tia phân giác của \(\widehat {BOD}\).
Mà \(\widehat {BOC}\) và \(\widehat {BOD}\) kề bù nên \(\widehat {AOE} = 90^\circ \).
Câu 51:
Tìm tất cả các giá trị thực của tham số m để điểm M( 2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y = 2x3 – 3(2m + 1)x2 + 6m(m + 1)x + 1 (C) một tam giác có diện tích nhỏ nhất.
 Xem đáp án
Xem đáp án
Ta có: y’ = 6x2 – 6(2m + 1)x + 6m(m + 1)
y’ = 0 \( \Leftrightarrow \)6x2 – 6(2m + 1)x + 6m(m + 1) = 0
\( \Leftrightarrow \)x2 – (2m + 1)x + m(m + 1) = 0
∆ = 4m2 + 4m + 1 – 4(m2 + m) = 1
Suy ra y’ = 0 có hai nghiệm: \[\left[ \begin{array}{l}{x_1} = \frac{{2m + 1 + 1}}{2} = m + 1\\{x_2} = \frac{{2m + 1 - 1}}{2} = m\end{array} \right.\].
Do đó hàm số luôn có cực đại và cực tiểu với mọi m.
+) Tọa độ các điểm cực đại và cực tiểu của đồ thị là: A(m; 2m3 + 3m2 + 1);
B(m + 1; 2m3 + 3m2).
Suy ra \(AB = \sqrt {{{(m - m - 1)}^2} + {{\left( {2{m^3} + 3{m^2} + 1 - 2{m^3} - 3{m^2}} \right)}^2}} = \sqrt 2 \).
Và phương trình đường thẳng AB là:
x + y – 2m3 – 3m2 – m – 1 = 0.
Do đó ∆MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
\({d_{(M;AB)}} = \frac{{\left| {2{m^3} + m - 2{m^3} - 3{m^2} - m - 1} \right|}}{{\sqrt 2 }} = \frac{{3{m^2} + 1}}{{\sqrt 2 }} \ge \frac{1}{{\sqrt 2 }}\).
Suy ra \(\min {d_{(M;AB)}} = \frac{1}{{\sqrt 2 }}\).
Dấu “=” xảy ra khi m = 0.
Vậy với m = 0 thì thỏa mãn yêu cầu bài toán.
Câu 52:
Cho tam giác ABC cân tại A (AB = AC). M là trung điểm của BC.
a) Chứng minh ∆AMB = ∆AMC và \(\widehat {BAM} = \widehat {CAM}\)
b) Qua M kẻ đường thẳng song song với AB cắt AC tại N. Chứng minh ∆MNC cân.
c) Chứng minh: N trung điểm của AC.
 Xem đáp án
Xem đáp án
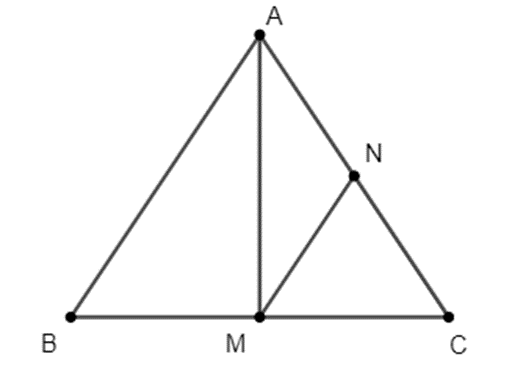
a) Xét ∆AMB và ∆AMC có:
AB = AC (do ∆ABC cân tại A)
AM là cạnh chung
BM = MC (do M là trung điểm của BC)
Do đó ∆AMB = ∆AMC (c.c.c)
Suy ra \(\widehat {BAM} = \widehat {CAM}\) (hai góc tương ứng)
b) Vì MN // AB (gt)
\( \Rightarrow \widehat B = \widehat {NMC}\) (đồng vị)
Mà \(\widehat B = \widehat C\) (do ∆ABC cân tại A)
\( \Rightarrow \widehat C = \widehat {NMC}\)
\( \Rightarrow \) ∆MNC cân tại N
c) Vì ∆MNC cân tại N (theo câu b))
\( \Rightarrow \) NC = NM (1)
Vì MN//AB (gt)
\( \Rightarrow \widehat {BAM} = \widehat {AMN}\) (so le trong)
Mà \(\widehat {BAM} = \widehat {CAM}\) (theo câu a))
\( \Rightarrow \widehat {CAM} = \widehat {AMN}\) hay \(\widehat {NAM} = \widehat {AMN}\)
\( \Rightarrow \) ∆MNA cân tại N
\( \Rightarrow \) AN = MN (2)
Từ (1) và (2) suy ra NC = AN
Mà điểm N nằm giữa hai điểm A và C.
Suy ra N là trung điểm của AC.
Câu 53:
Chứng minh rằng với mọi giá trị của m phương trình:
mx2 – (3m + 2)x + 1 = 0 luôn có nghiệm.
 Xem đáp án
Xem đáp án
Xét ∆ = 9m2 + 12m + 4 – 4m
= 9m2 + 8m + 4
Xét f(x) = 9m2 + 8m + 4 có:
\(\left\{ \begin{array}{l}\Delta ' = {4^2} - 9.4 = - 20 < 0\\a = 9 > 0\end{array} \right.\)
\( \Rightarrow \) f(x) > 0 \(\forall \)m ∈ ℝ
Suy ra ∆ > 0\(\forall \)m ∈ ℝ nên phương trình đã cho luôn có nghiệm.
Câu 54:
Một hình chữ nhật có chu vi 40 m, chiều dài hơn chiều rộng 4 m. Tính diện tích của hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Nửa chu vi hình chữ nhật là: 40 : 2 = 20 (m)
Chiều dài của hình chữ nhật là:
(20 + 4) : 2 = 12 (m)
Chiều rộng của hình chữ nhật là:
20 – 12 = 8 (m)
Vậy diện tích của hình chữ nhật là:
12.8 = 96 (m2)
Đáp số: 96 m2.
Câu 55:
Một ô tô cứ đi 100 km thì tiêu thụ hết 12,5l xăng. Hỏi ô tô đó đi quãng đường dài 60 km thì tiêu thụ hết bao nhiêu lít xăng?
 Xem đáp án
Xem đáp án
Ô tô đó đi 1 km thì tiêu thụ hết số lít xăng là:
12,5 : 100 = 0,125 (l)
Ô tô đó đi quãng đường dài 60 km thì tiêu thụ hết số lít xăng là:
0,125 . 60 = 7,5 (l)
Đáp số: 7,5 lít xăng
Câu 56:
1 sọt cam có quả trong khoảng từ 200 đến 600 quả. Nếu xếp vào mỗi dĩa 6 quả; 10 quả; 12 quả; 14 quả đều vừa đủ. Hỏi trong sọt có bao nhiêu quả cam?
 Xem đáp án
Xem đáp án
Gọi số quả cam là x (200 ≤ x ≤ 600, x ∈ ℕ)
Theo bài cho ta có x chia hết cho 6; 10; 12; 14
\( \Rightarrow \) x ∈ BC(6, 10, 12, 14)
Ta có 6 = 2.3; 10 = 2.5; 12 = 22.3; 14 = 2.7
\( \Rightarrow \) BCNN(6, 10, 12, 14) = 22.3.5.7 = 420
\( \Rightarrow \) x ∈ B(420) = {420; 840; …}
Mà 200 ≤ x ≤ 600 nên x = 420.
Vậy trong sọt có 420 quả cam.
Câu 57:
Theo kế hoạch trong dịp tết trồng cây, xã A phải trồng 1520 cây, nhưng xã A đã trồng được 2052 cây. Hỏi xã A đã vượt mức bao nhiêu phần trăm kế hoạch?
 Xem đáp án
Xem đáp án
Số câu xã A vượt kế hoặc là:
2052 – 1520 = 532 (cây)
Xã A đã vượt mức kế hoạch là:
532 : 1520 = 0,35 = 35%
Đáp số: 35%
Câu 58:
Nếu chỉ lấy đến 2 chữ số ở phần thập phân của thương thì phép chia
33,14 : 58 có số dư là bao nhiêu?
 Xem đáp án
Xem đáp án
Ta có:
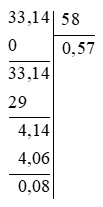
Vậy số dư của phép chia là: 0,08.
Câu 59:
Người ta viết liền nhau dãy các số tự nhiên bắt đầu từ 1; 2; 3; 4; … Hỏi chữ số thứ 659 là chữ số nào?
 Xem đáp án
Xem đáp án
Số các số từ 1 đến 9 là: 9 – 1 + 1 = 9 (số)
Số các số có hai chữ số là: 99 – 10 + 1 = 90 (số)
Số các số có ba chữ số là 999 – 100 + 1 = 900 (số)
Số các chữ số dùng để viết các số có 1 chữ số và có 2 chữ số trong dãy là:
9 + 90.2 = 189 (chữ số)
Số các chữ số dùng để viết các số có 1 chữ số, có 2 chữ số và có 3 chữ số trong dãy là:
9 + 90.2 + 900.3 = 2889 (chữ số)
Do 189 < 659 < 2889 nên ta viết đến các số có 3 chữ số.
Số các chữ số dùng để viết các số có 3 chữ số trong dãy số là: 659 – 189 = 470 (chữ số)
Số các số có 3 chữ số là: 470 : 3 = 156 (dư 2)
Điều đó có nghĩa là người ta đã viết được 156 số có 3 chữ số ngoài ra còn viết được đến chữ số thứ hai của số tiếp theo.
Số có 3 chữ số mà người ta viết được là: 156 + 100 – 1 = 255
Số liền sau 255 là 256, chữ số thứ hai của số là là 5.
Vậy chữ số thứ 659 là chữ số 5.
Câu 60:
Tính giá trị của biểu thức:
100 – {200 : [31 + 2.(4 – 7)] – 88}
 Xem đáp án
Xem đáp án
100 – {200 : [31 + 2.(4 – 7)] – 88}
= 100 – {200 : [31 + 2 .(-3)] – 88}
= 100 – {200 : [31 + (-6)] – 88}
= 100 – (200 : 25 – 88)
= 100 – (8 – 88)
= 100 – (–80)
= 180
Câu 61:
So sánh M và N biết: \(M = \frac{{{{100}^{100}} + 1}}{{{{100}^{99}} + 1}}\) và \(N = \frac{{{{100}^{101}} + 1}}{{{{100}^{100}} + 1}}\).
 Xem đáp án
Xem đáp án
• \(M = \frac{{{{100}^{100}} + 1}}{{{{100}^{99}} + 1}}\)\( = \frac{{{{100}^{100}} + 100 - 99}}{{{{100}^{99}} + 1}}\)
\( = \frac{{100({{100}^{99}} + 1) - 99}}{{{{100}^{99}} + 1}} = 100 - \frac{{99}}{{{{100}^{99}} + 1}}\).
• \(N = \frac{{{{100}^{101}} + 1}}{{{{100}^{100}} + 1}}\)\( = \frac{{{{100}^{101}} + 100 - 99}}{{{{100}^{100}} + 1}}\)
\( = \frac{{100({{100}^{100}} + 1) - 99}}{{{{100}^{100}} + 1}} = 100 - \frac{{99}}{{{{100}^{100}} + 1}}\)
Ta có: \(\frac{{99}}{{{{100}^{99}} + 1}} > \frac{{99}}{{{{100}^{100}} + 1}}\).
Do đó M < N.
Câu 62:
Cho hình thang ABCD, O là giao điểm của 2 đường chéo, đáy lớn CD. Đường thẳng qua A song song với BC cắt BD ở E và đường thẳng qua B song song với AD cắt đường thẳng AC tại F.
a) Chứng minh: EF // AB.
b) Chứng minh: AB2 = EF . CD.
 Xem đáp án
Xem đáp án
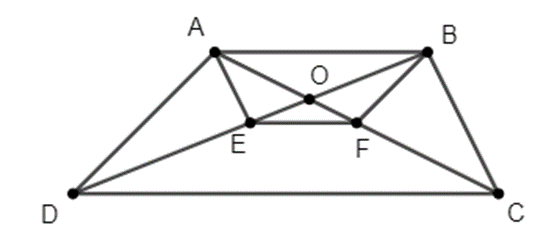
a) DO AE // BC nên áp dụng hệ quả định lí Ta-let, ta có:
\(\frac{{OE}}{{OB}} = \frac{{AO}}{{OC}}\)
Tương tự ta có: BF // AD
\(\frac{{OF}}{{OA}} = \frac{{OB}}{{OD}}\)
Mà AB // CD nên \(\frac{{OB}}{{OD}} = \frac{{OA}}{{OC}}\)
Từ đó suy ra \(\frac{{OF}}{{OA}} = \frac{{OE}}{{OB}} \Rightarrow \)EF // AB (đpcm).
b) Do AB // EF nên \(\frac{{EF}}{{AB}} = \frac{{OE}}{{OB}}\)
Do AB // CD nên \(\frac{{OA}}{{OC}} = \frac{{AB}}{{CD}}\)
Mà theo a) ta có: \(\frac{{OE}}{{OB}} = \frac{{AO}}{{OC}}\)
Nên \(\frac{{EF}}{{AB}} = \frac{{AB}}{{CD}}\)
Vậy AB2 = EF.CD (đpcm)
