- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 53)
-
12887 lượt thi
-
46 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
a) Tính bằng cách thuận tiện nhất:
0,12 × 400;
4,7 × 5,5 – 4,7 × 4,5
b) Tính nhẩm kết quả tìm x:
5,4 × x = 5,4
9,8 × x = 6,2 × 9,8.
 Xem đáp án
Xem đáp án
a) Ta có
0,12 × 400 = 0,12 × 100 × 4 = 12 × 4 = 48.
4,7 × 5,5 – 4,7 × 4,5 = 4,7 × (5,5 – 4,5) = 4,1 × 1 = 4,7.
b) Ta có 5,4 × x = 5,4
x = 1 (vì 5,4 × 1 = 5,4).
Ta có 9,8 × x = 6,2 × 9,8
x = 6,2 (hai tích bằng nhau đã có một thừa số bằng nhau thì thừa số còn lại cũng bằng nhau).
Câu 2:
Cho 101 đường thẳng, trong đó bất cứ hai đường thẳng nào cũng cắt nhau, không có ba đường thẳng nào đồng quy. Số giao điểm của chúng là bao nhiêu?
 Xem đáp án
Xem đáp án
Mỗi đường thẳng cắt 100 đường thẳng còn lại tạo nên 100 giao điểm.
Vì có 101 đường thẳng nên có 101 . 100 giao điểm
Nhưng mỗi giao điểm đã được tính hai lần nên chỉ có
101 . 100 : 2 = 5050 (giao điểm)
Vậy có 5050 giao điểm.
Câu 3:
Chứng minh các biểu thức sau dương:
a) x2 – 8x + 20.
b) 4x2 – 12x + 11.
c) x2 – x + 1.
d) x2 – 2x + y2 + 4y + 6.
 Xem đáp án
Xem đáp án
a) x2 – 8x + 20 = (x2 – 8x + 16) + 4 = (x + 4)2 + 4
Vì (x + 4)2 ≥ 0 với mọi x
Nên (x + 4)2 + 4 > 0 với mọi x
Vậy biểu thức x2 – 8x + 20 dương.
b) 4x2 – 12x + 11 = (4x2 – 12x + 9) + 2 = (2x – 3)2 + 2
Vì (2x – 3)2 ≥ 0 với mọi x
Nên (2x – 3)2 + 2 > 0 với mọi x
Vậy biểu thức 4x2 – 12x + 11 dương.
c) \[{{\rm{x}}^2} - x + 1 = {x^2} - 2.x.\frac{1}{2} + \frac{1}{4} + \frac{3}{4} = {\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4}\]
Vì \({\left( {x - \frac{1}{2}} \right)^2} \ge 0\) với mọi x
Nên \({\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4} > 0\) với mọi x
Vậy biểu thức x2 – x + 1 dương.
d) x2 – 2x + y2 + 4y + 6
= (x2 – 2x + 1) + (y2 + 4y + 4) + 1
= (x – 1)2 + (y + 2)2 + 1
Vì (x – 1)2 ≥ 0 với mọi x
(y + 2)2 ≥ 0 với mọi y
Nên (x – 1)2 + (y + 2)2 + 1 > 0 với mọi x, y
Vậy biểu thức x2 – 2x + y2 + 4y + 6 dương.
Câu 4:
Cho hai đường thẳng: y = x + 3 (d1); y = 3x + 7 (d2).
a) Gọi A và B lần lượt là giao điểm của (d1) và (d2) với trục Oy. Tìm tọa độ trung điểm I của đoạn thẳng AB.
b) Gọi J là giao điểm của (d1) và (d2) . Tam giác OIJ là tam giác gì? Tính diện tích của tam giác đó.
 Xem đáp án
Xem đáp án
a) Vì A là giao điểm của (d1) và Oy nên \(\left\{ \begin{array}{l}{x_A} = 0\\{y_A} = 0 + 3 = 3\end{array} \right.\)
Suy ra A(0; 3).
Vì B là giao điểm của (d2) và Oy nên \(\left\{ \begin{array}{l}{x_B} = 0\\{y_B} = 3.0 + 7 = 7\end{array} \right.\)
Suy ra B(0; 7).
Vì I là trung điểm của AB nên tọa độ của I là
\(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2}\\{y_B} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = \frac{{0 + 0}}{2} = 0\\{y_B} = \frac{{3 + 7}}{2} = 5\end{array} \right.\)
Vậy I(0; 5).
b) Ta có I(0; 5) suy ra OI = 5.
Hoành độ giao điểm của (d1) và (d2) là nghiệm của phương trình:
x + 3 = 3x + 7
⇔ x – 3x = 7 – 3
⇔ – 2x = 4
⇔ x = – 2
Suy ra y = – 2 + 3 = 1
Do đó J(– 2; 1), suy ra \[OJ = \sqrt {{{\left( { - 2} \right)}^2} + {1^2}} = \sqrt 5 \].
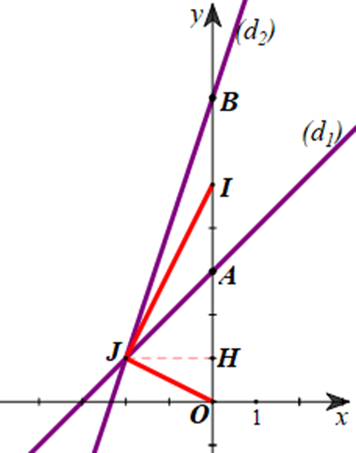
Gọi H là hình chiếu của J lên Oy. Do đó H(0; 1).
Suy ra OH = 1 và JH = 2.
Do đó IH = OI – OH = 5 – 1 = 4.
Khi đó, theo định lí Pythagore ta có: IJ2 = IH2 + JH2
\[ \Rightarrow IJ = \sqrt {I{H^2} + J{H^2}} = \sqrt {{4^2} + {2^2}} = 2\sqrt 5 \]
Suy ra OI2 = OJ2 + JI2
Do đó tam giác OIJ vuông tại J (định lý Pytago đảo)
Ta có \[{{\rm{S}}_{{\rm{OIJ}}}} = \frac{1}{2}JI.J{\rm{O}} = \frac{1}{2}.2\sqrt 5 .\sqrt 5 = 5\]
Vậy tam giác OIJ vuông tại J có diện tích bằng 5.
Câu 5:
Mua 0,5 kg nho và 1 kg táo phải trả 60 000 đồng. Mua 1 kg nho và 0,5 kg táo phải trả 72 000 đồng. Tính giá tiền mua 1 kg nho và giá tiền mua 1 kg táo.
 Xem đáp án
Xem đáp án
Tổng 1,5 kg nho và 1,5 kg táo phải trả:
60 000 + 72 000 = 132 000 (đồng)
Tổng 1 kg nho và 1 kg táo phải trả:
132 000 : 1,5 = 88 000 (đồng)
Giá tiền của 0,5 kg nho là:
88 000 – 60 000 = 28 000 (đồng)
Giá tiền 1 kg nho là:
28 000 × 2 = 56 000 (đồng)
Giá tiền 1 kg táo là:
60 000 – 28 000 = 32 000 (đồng)
Vậy 1 kg nho giá 56 000 đồng và 1 kg táo giá 32 000 đồng.
Câu 6:
Trung bình cộng của hai số là 12,35. Tìm hai số đó biết rằng hiệu của chúng bằng 3,3.
 Xem đáp án
Xem đáp án
Tổng 2 số đó là:
12,35 × 2 = 24,7
Số lớn là:
(24,7 + 3,3) : 2 = 14
Số bé là:
24,7 – 14 = 10,7
Vậy hai số cần tìm là 14 và 10,7.
Câu 7:
Tổng một số tự nhiên và 1 số thập phân là 62,42. Khi cộng hai số này một bạn quên mất dấu phẩy ở số thập phân nên đã đặt tính như số tự nhiên và được kết quả 3569. Tìm số tự nhiên và số thập phân đó.
 Xem đáp án
Xem đáp án
Tổng sai hơn tổng đúng là
3 569 – 62,42 = 3 506,58 (đơn vị)
Do tổng là 1 số thập phân có 2 chữ số sau dấu phẩy nên số thập phân có 2 chữ số sau dấu phẩy
Nếu quên dấu phẩy ở số thập phân thì được số mới gấp 100 lần số thập phân
Suy ra tổng sẽ tăng thêm 100 – 1 = 99 lần số thập phân, tương ứng là 3 506,58
Số thập phân là
3 506,58 : 99 = 35,42
Số tự nhiên là
62,42 – 35,42 = 27
Vậy hai số cần tìm là 35,42 và 27.
Câu 8:
Một con cá có đuôi cân nặng 0,25 kg; đầu cân nặng bằng đuôi và nửa thân; thân cân nặng bằng đầu và đuôi. Hỏi con cá cân nặng bao nhiêu kg?
 Xem đáp án
Xem đáp án
Vì đầu cân nặng bằng đuôi và nửa thân mà thân nặng bằng đầu và đuôi nên thân nặng bằng 2 đuôi và một nửa thân.
Suy ra nửa thân nặng bằng 2 đuôi
Nửa thân cá nặng là
0,25 × 2 = 0,5 (kg)
Cả thân cá nặng là
0,5 × 2 = 1 (kg)
Đầu cá nặng là
0,25 + 0,5 = 0,75 (kg)
Con cá nặng là
1 + 0,25 + 0,75 = 2 (kg)
Vậy con cá nặng 2 kg.
Câu 9:
Tính
a) 758,7 + 65,46.
b) 4,62 × 35,4.
c) 234,8 – 87.
d) 225,54 : 6,3 Xem đáp án
Xem đáp án
a) Ta có 758,7 + 65,46 = 824,16.
b) Ta có 4,62 × 35,4 = 163,548.
c) Ta có 234,8 – 87 = 147,8.
d) Ta có 225,54 : 6,3 = 35,8.
Câu 10:
 Xem đáp án
Xem đáp án
Ta có
(3965 – 2378) – (665 – 1378)
= 3965 – 2378 – 665 + 1378
= (3965 – 665) – (2378 – 1378)
= 3300 – 1000
= 2300.
Câu 11:
Một lớp có 60 em, 42 em biết bơi, 46 em biết đi xe đạp, 55 em biết chơi bóng. Hỏi có ít nhất bao nhiêu em biết cả 3 thứ?
 Xem đáp án
Xem đáp án
Số học sinh không biết bơi là: 60 – 42 = 18 (học sinh).
Số học sinh không biết đi xe đạp là: 60 – 46 = 14 (học sinh).
Số học sinh không biết chơi bóng là: 60 – 55 = 5 (học sinh).
Ít nhất có số học sinh biết cả 3 thứ là: 60 – 18 – 14 – 5 = 23 (học sinh).
Câu 12:
Tìm x:
a) 4x(3x – 7) – 6(2x2 – 5x + 1) = 12
b) (5x + 3)(4x – 1) + (10x – 7)(–2x + 3) = 27
c) (8x – 5)(3x + 2) – (12x + 7)(2x – 1) = 17
d) (5x + 9)(6x – 1) – (2x – 3)(15x + 1) = – 190.
 Xem đáp án
Xem đáp án
a) Ta có 4x(3x – 7) – 6(2x2 – 5x + 1) = 12
⇔ 12x2 – 28x – 12x2 + 30x – 6 = 12
⇔ 2x = 12 + 6
⇔ 2x = 18
⇔ x = 9
Vậy x = 9.
b) Ta có (5x + 3)(4x – 1) + (10x – 7)( – 2x + 3) = 27
⇔ 20x2 – 5x + 12x – 3 – 20x2 + 30x + 14x – 21 = 27
⇔ 51x = 27 + 21 + 3
⇔ 51x = 51
⇔ x = 1
Vậy x = 1.
c) Ta có (8x – 5)(3x + 2) – (12x + 7)(2x – 1) = 17
⇔ 24x2 + 16x – 15x – 10 – 24x2 + 12x – 14x + 7 = 17
⇔ – x = 17 – 7 + 10
⇔ x = – 20
Vậy x = – 10.
d) Ta có (5x + 9)(6x – 1) – (2x – 3)(15x + 1) = – 190
⇔ 30x2 + 54x – 5x – 9 – 30x2 + 45x – 2x + 3 = – 190
⇔ 92x = – 190 – 3 + 9
⇔ 92x = – 184
⇔ x = – 2
Vậy x = – 2.
Câu 13:
Tính
a) 653,38 + 96,92 = ……………………
35,069 – 14,235 = ……………………
b) 52,8 × 6,3 = ……………………
17,15 × 4,9 = ……………………
 Xem đáp án
Xem đáp án

Vậy 653,38 + 96,92 = 750,30
35,069 – 14,235 = 20,834
52,8 × 6,3 = 332,64
17,15 × 4,9 = 84,035.
Câu 14:
Tìm x biết
715,14 – (x × 5) = 147,04. Xem đáp án
Xem đáp án
Ta có: 715,14 – (x × 5) = 147,04
x × 5 = 715,14 – 147,04
x × 5 = 568,1
x = 568,1 : 5
x = 113,62
Vậy x = 113,62.
Câu 15:
Cho các số x, y thõa mãn đẳng thức 3x2 + 3y2 + 4xy + 2x – 2y + 2 = 0.
Tính M = (x + y)2010 + (x + 2)2011 + (y – 1)2012.
 Xem đáp án
Xem đáp án
Ta có 3x2 + 3y2 + 4xy + 2x – 2y + 2 = 0
⇔ (2x2 + 4xy + 2y2) + (x2 + 2x + 1) + (y2 – 2y + 1) = 0
⇔ 2(x + y)2 + (x + 1)2 + (y – 1)2 = 0
Vì (x + y)2 ≥ 0 với mọi x, y
(x + 1)2 ≥ 0 với mọi x
(y – 1)2 ≥ 0 với mọi y
Suy ra 2(x + y)2 + (x + 1)2 + (y – 1)2 ≥ 0 với mọi x, y
Do đó phương trình có nghiệm khi \(\left\{ \begin{array}{l}x + y = 0\\x + 1 = 0\\y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\)
Thay x = – 1, y = 1 vào M ta được
M = (x + y)2010 + (x + 2)2011 + (y – 1)2012
M = [(– 1) + 1]2010 + [(– 1) + 2]2011 + (1 – 1)2012
M = 0 + 1 + 0 = 1
Vậy M = 1.
Câu 16:
 Xem đáp án
Xem đáp án
Nếu không có 3 điểm nào thẳng hàng thì có tất cả
1000 . (1000 – 1) : 2 = 499 500 đường thẳng
Nhưng do có đúng 3 điểm thẳng hàng nên số đường thẳng nên bị hụt mất 2 đường thằng
Suy ra có 499 500 – 2 = 499 498 (đường thẳng)
Vậy có 499 498 đường thẳng tạo bởi 2 trong 1000 điểm đó.
Câu 17:
Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho \(BM = \frac{1}{3}AB\), trên cạnh AC lấy điểm N sao cho \(CN = \frac{1}{3}AC\). Nối B với N, C với M, hai đoạn thẳng BN và CM cắt nhau tại O. Hãy so sánh diện tích tam giác OMB và ONC.
 Xem đáp án
Xem đáp án
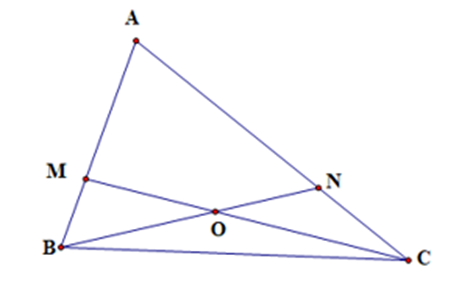
Vì \(BM = \frac{1}{3}AB\) nên \({S_{CMB}} = \frac{1}{3}{S_{ABC}}\)
\(CN = \frac{1}{3}AC\) nên \({S_{CNB}} = \frac{1}{3}{S_{ABC}}\)
Suy ra \({S_{CMB}} = {S_{NBC}}\)
Mà \({S_{CMB}} = {S_{OBC}} + {S_{BMO}}\), \({S_{CNB}} = {S_{OBC}} + {S_{CNO}}\)
Do đó \({S_{BMO}} = {S_{CNO}}\)
Vậy diện tích tam giác OMB bằng diện tích tam giác ONC.
Câu 18:
Cho đoạn thẳng AB, O là trung điểm AB. Trên cùng 1 nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là 1 điểm thuộc tia Ax. Đường vuông góc với OC cắt By tại D. Chứng minh rằng CD = AC + BD.
 Xem đáp án
Xem đáp án
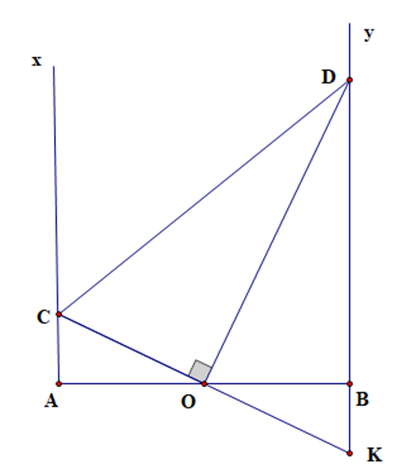
Gọi K là giao điểm của CO cà BD
Vì O là trung điểm của AB nên OA = OB
Vì Ax ⊥ AB nên \(\widehat {CAO} = 90^\circ \)
Vì By ⊥ AB nên \(\widehat {KBO} = 90^\circ \)
Xét △AOC và △BOK có
\(\widehat {CAO} = \widehat {KBO}\left( { = 90^\circ } \right)\)
OA = OB (chứng minh trên)
\(\widehat {COA} = \widehat {BOK}\) (hai góc đối đỉnh)
Do đó △AOC = △BOK (g.c.g)
Suy ra OC = OK, AC = BK (các cặp cạnh tương ứng)
Xét △DOC và △DOK có
OC = OK (chứng minh trên)
\(\widehat {COD} = \widehat {DOK}\left( { = 90^\circ } \right)\)
OD là cạnh chung
Do đó △DOC = △DOK (c.g.c)
Suy ra CD = DK (hai cạnh tương ứng)
Ta có CD = DK = BD + BK = BD + AC
Vậy CD = AC + BD.
Câu 19:
Có 4 bạn Hoa, Mai, Lan, Phượng. Các bạn Hoa, Mai, Lan cân nặng tất cả là 108,6 kg. Các bạn Mai, Lan, Phượng cân nặng hết tất cả 105,4 kg. Các bạn Hoa, Mai, Phượng cân nặng tất cả là 110,3 kg. Các bạn Hoa, Lan, Phượng cân nặng tất cả là 107,7 kg. Hỏi mỗi bạn nặng bao nhiêu kg?
 Xem đáp án
Xem đáp án
Tổng số cân nặng của 4 bạn là:
(108,6 + 105,4 + 107,7 + 110,3) : 3 = 144 (kg)
Phượng cân nặng là:
144 – 108,6 = 35,4 (kg)
Hoa cân nặng là :
144 – 105,4 = 38,6 (kg)
Mai cân nặng là:
144 – 107,7 = 36,3 (kg)
Lan cân nặng là:
144 – 110,3 = 33,7 (kg)
Vậy Phượng nặng 35,4 kg; Hoa nặng 38,6 kg;Mai nặng 36,3 kg; Lan nặng 33,7 kg.
Câu 20:
Cho biết x và y là 2 đại lượng tỉ lệ thuận và khi x = 4 thì y = 2 .Vậy hệ số tỉ lệ của x đối với y là k bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Có x = 4 và y = 2
Mà x và y là 2 đại lượng tỉ lệ thuận
Suy ra x = k . y
Hay 4 = k . 2
Suy ra k = 2
Vậy hệ số tỉ lệ của x đối với y là k = 2.
Câu 21:
Giữa các số 7 và 35 hãy tìm thêm 6 số nữa để được một cấp số cộng.
 Xem đáp án
Xem đáp án
Ta có: u1 = 7, u8 = 35
Suy ra 35 = 7 + (8 – 1)d
⇔ 35 = 7 + 7d
⇔ d = 4
Khi đó
u2 = u1 + d = 7 + 4 = 11
u3 = u1 + 2d = 7 + 8 = 15
u4 = u1 + 3d = 7 + 12 = 19
u5 = u1 + 4d = 7 + 16 = 23
u6 = u1 + 5d = 7 + 20 = 27
u7 = u1 + 6d = 7 + 24 = 31
Vậy 6 số cần đặt thêm là 11, 15, 19, 23, 27, 31.
Câu 22:
Hiện nay tổng số tuổi 2 bố con là 48 tuổi. Biết tuổi con có bao nhiêu ngày thì bố có mấy nhiều tuần. Tính tuổi mỗi người hiện nay.
 Xem đáp án
Xem đáp án
1 tuần = 7 ngày
Suy ra tuổi bố gấp 7 lần tuổi con
Tổng số phần bằng nhau là:
7 + 1 = 8 (phần)
Giá trị 1 phần cũng là tuổi con hiện nay:
48 : 8 = 6 (tuổi)
Tuổi bố hiện nay là:
6 × 7 = 42 (tuổi)
Vậy hiện nay con 6 tuổi, bố 42 tuổi.
Câu 23:
Một số gấp lên 9 lần rồi bớt đi 13 thì được 50. Giá trị của số đó là:
 Xem đáp án
Xem đáp án
Gọi số cần tìm là x
Ta có
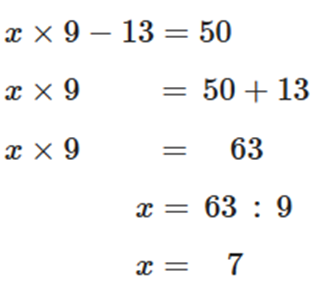
Vậy ta chọn đáp án D.
Câu 24:
Mua 4 m vải phải trả 44 000 đồng. Hỏi mua 7,8 m vải phải trả nhiều hơn bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Mua 1 m vải mất số tiền là:
44 000 : 4 = 11 000 (đồng)
Mua 7,8 m vải mất số tiền là:
11 000 × 7,8 = 85 800 (đồng)
Mua 7,8 m vải phải trả nhiều hơn số tiền là:
85 800 – 44 000 = 41 800 (đồng)
Vậy mua 7,8 m vải phải trả nhiều hơn số tiền là 41 800 đồng.
Câu 25:
Một cửa hàng có 20,430 kg mì chính được đóng gói vào 45 gói cân nặng bằng nhau. Cửa hàng đã bán 18 gói. Hỏi cửa hàng còn lại bao nhiêu kg mì chính?
 Xem đáp án
Xem đáp án
1 gói mì chính nặng số ki – lô – gam là:
20,430 : 45 = 0,454 (kg)
18 gói mì chính nặng số ki – lô – gam là:
0,454 × 18 = 8,172 (kg)
Cửa hàng còn lại số ki – lô – gam mì chính là:
20,430 – 8,172 = 12,258 (kg)
Vậy cửa hàng còn lại 12,258 kg mì chính.
Câu 26:
Một thửa ruộng hình chữ nhật có chiều rộng bằng cạnh của hình vuông có diện tích 64 m2, chiều dài gấp 3,5 lần chiều rộng. Tính diện tích thửa ruộng hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Chiều rộng hình chữ nhật hay cạnh hình vuông là 8 (m) (8 × 8 = 64)
Chiều dài hình chữ nhật là:
8 × 3,5 = 28 (m)
Diện tích thửa ruộng hình chữ nhật là
8 × 28 = 224 (m2)
Vậy diện tích thửa ruộng hình chữ nhật đó là 224 m2.
Câu 27:
Cho hai số có hai chữ số. Biết rằng, số thứ nhất bằng hiệu của 66 và số lẻ nhỏ nhất có hai chữ số. Số thứ hai là số liền trước của số lớn nhất có hai chữ số. Nếu lấy số thứ hai trừ số thứ nhất ta thu được kết quả bao nhiêu?
 Xem đáp án
Xem đáp án
Số lẻ nhỏ nhất có hai chữ số là số 11.
Vì số thứ nhất bằng hiệu của 66 và số lẻ nhỏ nhất có hai chữ số nên số thứ nhất là 66 – 11 = 55.
Số lớn nhất có hai chữ số là 99, số liền trước của 99 là 98.
Vì số thứ hai là số liền trước của số lớn nhất có hai chữ số nên số thứ hai là 98.
Hiệu của số thứ hai và số thứ nhất là
98 – 55 = 43
Vậy số thứ hai trừ số thứ nhất ta thu được kết quả là 43.
Câu 28:
Tính bằng hai cách
a) (6,75 + 3,25) × 4,2;
b) (9,6 – 4,2) × 3,6.
 Xem đáp án
Xem đáp án
a) Cách 1:
(6,75 + 3,25) × 4,2
= 10 × 4,2
= 42.
Cách 2:
(6,75 + 3,25 ) × 4,2
= 6,75 × 4,2 + 3,25 × 4,2
= 28,35 + 13,65
= 42.
b) Cách 1:
(9,6 – 4,2) × 3,6
= 5,4 × 3,6
=19,44
Cách 2:
(9,6 – 4,2) × 3,6
= 9,6 × 3,6 – 4,2 × 3,6
= 34,56 – 15,12
= 19,44.
Câu 29:
Tổng của hai số là 80, nếu tăng số thứ nhất lên 4 lần, số thứ hai tăng lên 5 lần thì được tổng mới là 360. Tìm hai số đó.
 Xem đáp án
Xem đáp án
Gọi x là số thứ nhất
Suy ra số thứ 2 là: 80 – x
Ta có :
4x + (80 – x) . 5 = 360
⇔ 4x + 400 – 5x = 360
⇔ x = 40
Do đó số thứ nhất là 40
Suy ra số thứ hai là 40
Vậy hai số cần tìm là 40 và 40.
Câu 30:
Rút gọn phân thức: \(\frac{{{x^2} + {y^2} + {z^2} - 2{\rm{x}}y + 2{\rm{xz}} - 2yz}}{{{x^2} - 2{\rm{x}}y + {y^2} - {z^2}}}\).
 Xem đáp án
Xem đáp án
Ta có
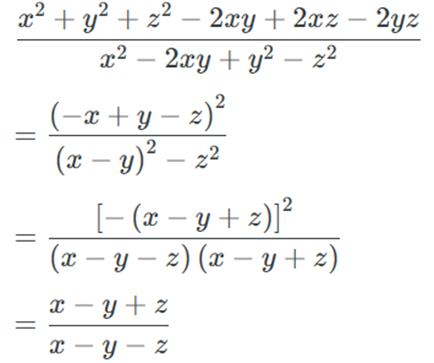
Vậy \(\frac{{{x^2} + {y^2} + {z^2} - 2{\rm{x}}y + 2{\rm{xz}} - 2yz}}{{{x^2} - 2{\rm{x}}y + {y^2} - {z^2}}} = \frac{{x - y + z}}{{x - y - z}}.\)
Câu 31:
 Xem đáp án
Xem đáp án
Ta có xy3 + y2 + 4xy = 6
⇔ xy3 + y2 + 4xy + 4 = 6 + 4
⇔ y2(xy + 1) + 4(xy + 1) = 10
⇔ (xy + 1)(y2 + 4) = 10 = 5 . 2 = (– 5) . (– 2)
Vì y2 + 4 ≥ 4 với mọi y
Nên \(\left\{ \begin{array}{l}xy + 1 = 2\\{y^2} + 4 = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}xy = 1\\{y^2} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}xy = 1\\\left[ \begin{array}{l}y = 1\\y = - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right.\\\left\{ \begin{array}{l}x = - 1\\y = - 1\end{array} \right.\end{array} \right.\)
Vậy (x; y) ∈ {(1; 1); (–1; –1)}.
Câu 32:
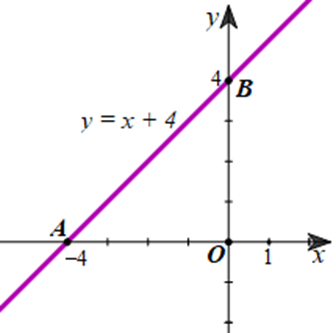
Vẽ đồ thị hàm số y = x + 4.
 Xem đáp án
Xem đáp án
• Với x = 0 thì y = 0 + 4 = 4.
Suy ra đồ thị hàm số cắt trục tung tại điểm B(0; 4)
• Với y = 0 thì x = 0 – 4 = – 4
Suy ra đồ thị hàm số cắt trục hoành tại điểm A(– 4; 0)
Ta có đồ thị hàm số y = x + 4
Câu 33:
Đúng ghi Đ, sai ghi S:
a) Số gồm 3 chục nghìn, 4 nghìn, 5 đơn vị viết là:
34050 … 34005 … 34500 …
b) Số gồm 9 chục nghìn, 3 nghìn, 2 trăm, 4 đơn vị viết là:
93204 … 93024 … 93424 ….
 Xem đáp án
Xem đáp án
a) Số gồm 3 chục nghìn, 4 nghìn, 5 đơn vị viết là:
34050 S 34005 Đ 34500 S
b) Số gồm 9 chục nghìn, 3 nghìn, 2 trăm, 4 đơn vị viết là:
93204 Đ 93024 S 93424 S.
Câu 34:
Trong mỗi buổi liên hoan, ban tổ chức đã mua 96 cái kẹo, 36 cái bánh và chia đều ra các đĩa, mỗi đĩa gồm cả kẹo và bánh. Có thể chia được nhiều nhất thành bao nhiêu đĩa, mỗi đĩa có bao nhiêu cái kẹo, bao nhiêu cái bánh ?
 Xem đáp án
Xem đáp án
Gọi số đĩa là a (a ∈ ℕ*)
Theo bài ra ta có: 96 ⋮ a; 36 ⋮ a và a lớn nhất
Ta có: 96 = 25 . 3 và 36 = 22 . 32
Suy ra ƯCLN(96, 36) = 22 . 3 = 4 . 3 = 12
Do đó có thể chia nhiều nhất thành 12 đĩa
Mỗi đĩa có số kẹo là:
96 : 12 = 8 (cái)
Mỗi đĩa có số bánh là:
36 : 12 = 3 (cái)
Vậy mỗi đĩa có 8 cái kẹo và 3 cái bánh.
Câu 35:
Để đánh số trang một quyển sách dùng hết 831 chữ số. Hỏi quyển sách đó có bao nhiêu trang?
 Xem đáp án
Xem đáp án
Từ trang 1 đến trang 9 có:
(9 – 1) : 1 + 1 = 9 (trang có 1 chữ số)
Từ trang 10 đến trang 99 có:
(99 – 10) : 1 + 1 = 90 (trang có 2 chữ số)
Từ trang 1 đến trang 99 cần dùng:
1 × 9 + 2 × 90 = 189 (chữ số)
Số chữ số của các trang có 3 chữ số là:
831 – 189 = 642 (chữ số)
Số các trang có 3 chữ số là:
642 : 3 = 214 (trang)
Quyển sách có số trang là:
9 + 90 + 214 = 313 (trang)
Vậy quyển sách đó có 313 trang.
Câu 36:
Cho tam giác ABC. Tia phân giác của góc B và góc C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB tại D và AC tại E. Chứng minh DE = BD + CE.
 Xem đáp án
Xem đáp án
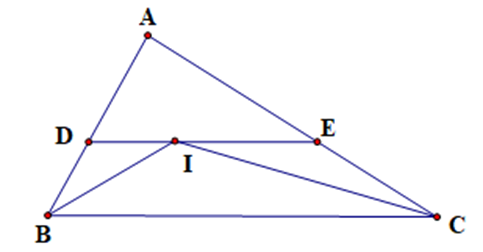
Vì BI là tia phân giác của \(\widehat {ABC}\)
Nên \(\widehat {ABI} = \widehat {IBC} = \frac{1}{2}\widehat {ABC}\)
Vì CI là tia phân giác của \(\widehat {ACB}\)
Nên \(\widehat {ACI} = \widehat {ICB} = \frac{1}{2}\widehat {ACB}\)
Vì DI // BC nên \(\widehat {DIB} = \widehat {IBC}\) (hai góc so le trong)
Mà \(\widehat {ABI} = \widehat {IBC}\) (chứng minh trên)
Suy ra \(\widehat {DIB} = \widehat {IBD}\)
Do đó tam giác BDI cân ở D
Suy ra DI = DB
Vì EI // BC nên \(\widehat {EIC} = \widehat {ICB}\) (hai góc so le trong)
Mà \(\widehat {ACI} = \widehat {ICB}\) (chứng minh trên)
Suy ra \(\widehat {EIC} = \widehat {ECI}\)
Do đó tam giác EIC cân ở E
Suy ra EI = EC
Ta có DE = DI + IE = BD + CE
Vậy DE = BD + CE.
Câu 37:
Làm theo mẫu:
\(\frac{{43}}{5} = \frac{{86}}{{10}} = 8,6\)
\(\frac{2}{{25}} = ...\)
\(\frac{{111}}{{125}} = ...\)
\(\frac{{23}}{8} = ...\)
\(\frac{{76}}{4} = ...\)
\(\frac{{42}}{{25}} = ...\)
\(\frac{{370}}{{50}} = ...\).
 Xem đáp án
Xem đáp án
Ta có:
\(\frac{2}{{25}} = \frac{8}{{100}} = 0,08\)
\(\frac{{111}}{{125}} = \frac{{888}}{{1000}} = 0,888\)
\(\frac{{23}}{8} = \frac{{2875}}{{1000}} = 2,875\)
\(\frac{{76}}{4} = \frac{{1900}}{{100}} = 19\)
\(\frac{{42}}{{25}} = \frac{{168}}{{100}} = 1,68\)
\(\frac{{370}}{{50}} = \frac{{740}}{{100}} = 7,4.\)
Câu 38:
Số học sinh khối 6 của một trường khoảng từ 400 đến 500 em. Mỗi lần xếp hàng 6 hoặc hàng 9 đều dư 2 em nhưng khi xếp hàng 5 thì vừa đủ. Tính số học sinh khối 6 của trường đó.
 Xem đáp án
Xem đáp án
Gọi số học sinh khối 6 trường đó là x (em, x ∈ ℕ, 400 < x < 500).
Vì mỗi lần xếp hàng 6 hoặc hàng 9 đều dư 2 em nhưng khi xếp hàng 5 thì vừa đủ
Suy ra x ⋮ 5 và x – 2 chia hết cho 6, 9
Vì x – 2 chia hết cho 6, 9
Nên x – 2 là bội chung của 6 và 9
Ta có: 6 = 2 . 3 và 9 = 32
Suy ra BCNN(6, 9) = 2 . 32 = 18
Do đó x – 2 ∈ B(18) = {0; 18; 36; ...; 414; 432; 450; 468; 486; ...}
Suy ra x ∈ {2; 20; 38; ...; 416; 434; 452; 470; 488;…}
Mà 400 < x < 500, x ⋮ 5
Suy ra x = 470
Vậy số học sinh khối 6 trường đó là 470 học sinh.
Câu 39:
Biết rằng \(\frac{3}{5}\) diện tích trồng nhãn của một xã là 6 ha. Hỏi diện tích trồng nhãn của xã đó là bao nhiêu mét vuông?
 Xem đáp án
Xem đáp án
Coi 6 ha tương ứng bằng 3 đoạn thẳng dài như nhau thì mỗi đoạn thẳng tương ứng:
6 : 3 = 2 (ha)
Diện tích trồng nhãn của xã tương ứng bằng 5 đoạn thẳng và bằng:
2 × 5 = 10 (ha) = 100 000 (m2)
Vậy diện tích trồng nhãn của xã đó là 100 000 m2.Câu 40:
Số học sinh khối lớp 6 của một trường trong khoảng từ 200 đến 300 học sinh, khi xếp thành các hàng 10; 12 và 15 người đều thừa 5 em. Tính số học sinh khối lớp 6.
 Xem đáp án
Xem đáp án
Gọi x là số học sinh khối lớp 6 của trường (học sinh; x ∈ ℕ, 200 ≤ x ≤ 300)
Khi xếp thành hàng 10 thừa 5 em thì x chia 10 dư 5 hay (x – 5) ⁝ 10
Khi xếp thành hàng 12 thừa 5 em thì x chia 12 dư 5 hay (x – 5) ⁝ 12
Khi xếp thành hàng 15 thừa 5 em thì x chia 15 dư 5 hay (x – 5) ⁝ 15
Do đó (x – 5) là bội chung của 10; 12 và 15
Ta có: 10 = 2 . 5; 12 = 22 . 3; 15 = 3 . 5
BCNN(10, 12, 15) = 22 . 3 . 5 = 60
Khi đó (x – 5) ∈ B(60) = {0; 60; 120; 180; 240; 300; 360;…}
Suy ra x ∈ {5; 65; 125; 185; 245; 305; 365;…}
Vì số học sinh trong trường khoảng từ 200 đến 300 học sinh nên 200 ≤ x ≤ 300
Do đó x = 245
Vậy số học sinh trong trường là 245 em.
Câu 41:
Tìm 2 phân số có tử số cùng là 1, mẫu số là 2 số tự nhiên liên tiếp sao cho \(\frac{2}{{13}}\) nằm giữa 2 phân số đó.
 Xem đáp án
Xem đáp án
Ta có \(\frac{2}{{13}} = 1:\frac{{13}}{2}\)
Suy ra mẫu số thứ nhất phải nhỏ hơn \(\frac{{13}}{2}\) và mẫu số thứ hai phải lớn hơn \(\frac{{13}}{2}\)
Ta có \(\frac{{13}}{2} = 6,5\)
Suy ra hai mẫu số cần tìm là 6 và 7
Vậy hai phân số đó là \(\frac{1}{6};\frac{1}{7}.\)
Câu 42:
Một can nhựa chứa 10 lít nước mắm. Biết 1 lít cân nặng 0,9 kg; can rỗng nặng 0,5 kg. Hỏi can nước mắm nặng mấy kg?
 Xem đáp án
Xem đáp án
10 lít nước mắm cân nặng là:
0,9 × 10 = 9 (kg)
Can nước mắm cân nặng là:
9 + 0,5 = 9,5 (kg)
Vậy can nước mắm nặng 9,5 kg.
Câu 43:
Cho a là một số nguyên âm. Hỏi b là số nguyên âm hay số nguyên dương nếu biết:
a) a . b là một số nguyên dương?
b) a . b là một số nguyên âm?
 Xem đáp án
Xem đáp án
a) a . b là số nguyên dương nên a và b cùng dấu
Mà a là số nguyên âm nên b cũng là số nguyên âm.
b) a . b là số nguyên âm nên a và b trái dấu
Mà a là số nguyên âm nên b là số nguyên dương.
Câu 44:
Cho đường tròn (O) và dây cung AB của (O) không là đường kính. Gọi I là trung điểm của AB. Một đường thẳng thay đổi đi qua A cắt đường tròn tâm O bán kính OI tại P và Q.
a) Chứng minh rằng AP . AQ = AI2.
b) Giả sử đường tròn ngoại tiếp tam giác BPQ cắt AB tại K khác B. Chứng minh
rằng AK . AB = AP . AQ.
c) Chứng minh rằng K là trung điểm của AI.
 Xem đáp án
Xem đáp án
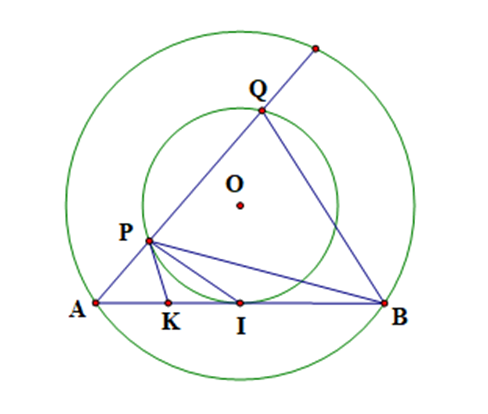
a) Xét (O; OA) có I là trung điểm của dây cung AB, suy ra OI ⊥ AB
Xét (O; OI) có OI ⊥ AI
Suy ra AI là tiếp tuyến của (O; OI) tại I
Do đó \(\widehat {PIA} = \widehat {PQI}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung PI)
Xét DAIP và DAQI có
\(\widehat {PIA} = \widehat {PQI}\) (chứng minh trên);
\(\widehat {PAI}\) là góc chung
Suy ra (g.g)
Do đó \(\frac{{AI}}{{AQ}} = \frac{{AP}}{{AI}}\), suy ra AP . AQ = AI2
b) Vì BKPQ là tứ giác nội tiếp nên \(\widehat {APK} = \widehat {KBQ}\)
Xét DAPK và DABQ có
\(\widehat {APK} = \widehat {ABQ}\) (chứng minh trên);
\(\widehat {PAK}\) là góc chung
Suy ra (g.g)
Do đó \(\frac{{AP}}{{AB}} = \frac{{AK}}{{AQ}}\), suy ra AP . AQ = AB . AK.
c) Ta có AP . AQ = AB . AK (chứng minh câu b)
AP . AQ = AI2 (chứng minh câu a)
Suy ra AB . AK = AI2
⇔ 2AI . AK = AI2 (vì I là trung điểm của AB)
⇔ 2AK = AI
\( \Rightarrow AK = \frac{1}{2}AI\)
Vậy K là trung điểm của AI.
Câu 45:
Hình lập phương có diện tích toàn phần là 54 cm2 . Tính thể tích hình đó.
 Xem đáp án
Xem đáp án
Diện tích một mặt của hình lập phương là:
54 : 6 = 9 (cm2)
Vì 9 = 3 × 3 nên cạnh hình lập phương là 3 cm
Thể tích của hình lập phương là :
3 × 3 × 3 = 27 (cm3)
Vậy thể tích hình lập phương đó là 27 cm3.
Câu 46:
Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD
a) Chứng minh rằng MNPQ là hình bình hành
b) Hình thang ABCD phải có thêm điều kiện gì để tứ giác MPNQ là hình thoi.
 Xem đáp án
Xem đáp án
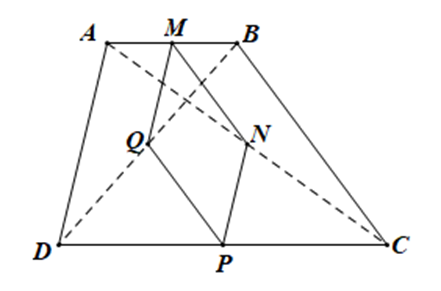
a) Xét tam giác BAD có: M, Q lần lượt là trung điểm của AB, BD
Suy ra MQ là đường trung bình của tam giác BAD
Do đó MQ // AD và \(MQ = \frac{1}{2}A{\rm{D}}\) (1)
Xét tam giác CAD có: N, P lần lượt là trung điểm của AC, CD
Suy ra NP là đường trung bình của tam giác CAD
Do đó NP // AD và \(NP = \frac{1}{2}A{\rm{D}}\) (2)
Từ (1) và (2) suy ra MQ // NP ; MQ = NP
Xét tứ giác MNPQ có: MQ // NP ; MQ = NP (chứng minh trên)
Suy ra MNPQ là hình bình hành
b) Xét tam giác CAB có: N, M là trung điểm của AC, AB
Suy ra NM là đường trung bình của tam giác CAB
Do đó \(NM = \frac{1}{2}BC\)
Để MPNQ là hình thoi ⇔ MN = MQ
⇔ AD = BC (vì \(MQ = \frac{1}{2}A{\rm{D,}}MN = \frac{1}{2}BC\))
⇔ Hình thang ABCD là hình thang cân
Vậy hình thang ABCD cân thì MNPQ là hình bình hành.
