- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 58)
-
12933 lượt thi
-
94 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Hòa và bình có tất cả 120 viên bi. Biết rằng nếu hòa cho bình 10 viên bi thì số viên bi của hai bạn sẽ bằng nhau. Hỏi mỗi bạn có bao nhiêu viên bi?
 Xem đáp án
Xem đáp án
Nếu Hòa cho Bình 10 viên bi thì số bi của hai bạn bằng nhau nên ban đầu Hoà hơn Bình số bi là:
2 . 10 = 20 (viên)
Số bi của Hoà ban đầu là:
(120 + 20) : 2 = 70 (viên)
Số bi của Bình ban đầu là:
70 – 20 = 50 (viên)
Đáp số: Hoà: 70 viên; Bình: 50 viên.
Câu 2:
Trong mặt phẳng tọa độ, cho tam giác có ba đỉnh A(3; 4), B(5; 1), C(–1; – 2). Lập phương trình tổng quát của đường cao kẻ từ A của tam giác ABC.
 Xem đáp án
Xem đáp án
Gọi AH là đường cao kẻ từ A xuống BC (H thuộc BC).
Đường cao AH đi qua điểm A (3; 4) và có vectơ pháp tuyến chính là vectơ chỉ phương của đường thẳng BC
\(\overrightarrow {{n_{AH}}} = \overrightarrow {BC} \)= (–6; –3) = –3(2; 1).
Phương trình tổng quát của AH là:
2 (x – 3) + y – 4 = 0 hay 2x + y – 10 = 0.
Câu 3:
Trong mặt phẳng tọa độ, cho tam giác có ba đỉnh A(3; 4), B(5; 1), C(–1; – 2). Lập phương trình tham số của đường thẳng đi qua B và song song với AC.
 Xem đáp án
Xem đáp án
Gọi đường thẳng đi qua B và song song với AC là d.
Ta có: d // AC nên \(\overrightarrow {{u_d}} = \overrightarrow {AC} \)= (–4; –6) = –2(2; 3)
Phương trình tham số của d là: \(\left\{ \begin{array}{l}x = 5 + 2t\\y = 1 + 3t\end{array} \right.\).
Câu 4:
Tìm số tự nhiên x biết: 14x = \(\frac{{{{14}^9}}}{{2744}}\)
 Xem đáp án
Xem đáp án
Ta có: 2744 = 23 . 73 = 143
Suy ra: 14x = \[\frac{{{{14}^9}}}{{2744}} = \frac{{{{14}^9}}}{{{{14}^3}}} = {14^6}\]
Vậy x = 6.
Câu 7:
Cho hai tập khác rỗng: A = (m – 1; 4]; B = (–2; 2m + 2), với m ∈ ℝ. Xác định m để A ∩ B = ∅.
 Xem đáp án
Xem đáp án
Vì tập A khác rỗng nên ta có m – 1 < 4 hay m < 5 (1)
Vì tập B khác rỗng nên ta có –2 < 2m + 2.
⇔ –4 < 2m.
⇔ m > –2 (2)
Từ (1) và (2), ta suy ra tập hợp A và B đều khác rỗng khi và chỉ khi –2 < m < 5 (*).
Để A ∩ B ≠ ∅ thì m – 1 < 2m + 2.
Nghĩa là, m > –3 (**).
Giao (*) và (**) lại với nhau, ta thu được kết quả –2 < m < 5.
Câu 8:
A = 2 + 22 + 23 + … + 2100. Tìm x biết 2(A + 2) = 22x.
 Xem đáp án
Xem đáp án
Ta có: 2A = 22 + 23 + … + 2101
2A – A = (22 + 23 + … + 2101) – (2 + 22 + 23 + … + 2100)
A = 2101 – 2
Thay A vào 2 (A + 2) = 22x ta có:
2(2101 – 2 + 2) = 22x
Hay 2102 = 22x
Vậy x = 102 : 2 = 51.
Câu 9:
Đường thẳng xx' cắt đường thẳng yy' tại O. Vẽ tia phân giác Ot của \(\widehat {xOy}\).
a) Gọi Ot' là tia đối của tia Ot. So sánh \(\widehat {xOt'}\)và \(\widehat {t'Oy}\).
b) Vẽ tia phân giác Om của \(\widehat {xOy}\) Tính góc \(\widehat {mOt}\).
 Xem đáp án
Xem đáp án
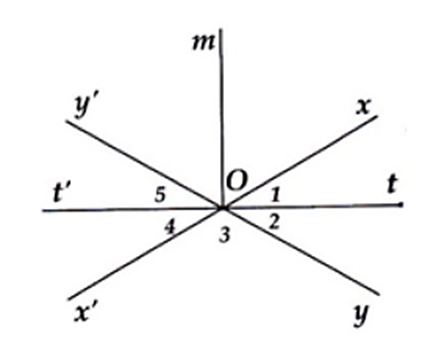
a) Ta có: \[\widehat {{O_1}} = \frac{{\widehat {xOy}}}{2}\]
Mà \(\widehat {{O_1}} = \widehat {{O_2}}\)(2 góc đối đỉnh)
\(\widehat {xOy} = \widehat {x'Oy'}\)(2 góc đối đỉnh)
\(\widehat {{O_4}} = \widehat {{O_5}}\)
Lại có:
\[\widehat {xOt'} = \widehat {xOy'} + \widehat {{O_5}}\]và \[\widehat {yOt'} = \widehat {x'Oy} + \widehat {{O_4}}\]
Mà \(\widehat {xOy'} = \widehat {x'Oy}\)(2 góc đối đỉnh) và \(\widehat {{O_4}} = \widehat {{O_5}}\)
Suy ra: \[\widehat {xOt'} = \widehat {t'Oy}\]
b) Vì \[\widehat {xOm} = \frac{1}{2}\widehat {xOy'}\,\,;\,\,\,\widehat {{O_1}} = \frac{1}{2}\widehat {xOy}\]nên
\[\widehat {tOm} = \widehat {xOm} + \widehat {{O_1}} = \frac{1}{2}\left( {\widehat {xOy'} + \widehat {xOy}} \right)\]= 90°.
Câu 10:
1 con bò nặng \(\frac{4}{7}\) con bò đó và 9 yến. Hỏi con bò đó nặng bao nhiêu tạ, bao nhiêu kg?
 Xem đáp án
Xem đáp án
9 yến tương đương với số phần con bò là:
1 – \(\frac{4}{7}\)= \(\frac{3}{7}\)(con bò)
Con bò nặng số yến là:
9 : \(\frac{3}{7}\) = 21 (yến)
Đổi 21 yến = 210 kg = 2,1 tạ.
Câu 11:
Một hình bình hành có cạnh đáy dài hơn chiều cao 12 cm. Chiều cao bằng \(\frac{5}{7}\) cạnh đáy. Hãy tính diện tích hình bình hành đó.
 Xem đáp án
Xem đáp án
Cạnh đáy hình bình hành là: 12 : (7 – 5) . 7 = 42 (cm)
Chiều cao hình bình hành là : 42 – 12 = 30 (cm)
Diện tích hình bình hành: 42 . 12 = 504 (cm2).
Câu 12:
Một viên gạch hình vuông cạnh 40 cm. Tính diện tích 10 viên gạch đó?
 Xem đáp án
Xem đáp án
Diện tích một viên gạch là:
40 . 40 = 1600 (cm2)
Diện tích 10 viên gạch đó là:
1600 . 10 = 16000 (cm2)
Câu 13:
Nêu định nghĩa n!.
 Xem đáp án
Xem đáp án
n! ta gọi là n giai thừa, là tích gồm các thừa số từ 1 đến n
n! = 1.2.3.4….n
Câu 14:
Tìm 1 số có 8 chữ số \(\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}{a_7}{a_8}} \)thỏa mãn: \[\overline {{a_1}{a_2}{a_3}} = \,{\left( {\overline {{a_7}{a_8}} } \right)^2}\]và \[\overline {{a_4}{a_5}{a_6}{a_7}{a_8}} = \,{\left( {\overline {{a_7}{a_8}} } \right)^3}\].
 Xem đáp án
Xem đáp án
Theo 2 giả thiết đề bài cho ta có:
\[\overline {{a_1}{a_2}{a_3}} = \,{\left( {\overline {{a_7}{a_8}} } \right)^2}\]
⇔ 100 ≤ \[{\left( {\overline {{a_7}{a_8}} } \right)^2}\]≤ 999
⇔ 10 ≤ \[\overline {{a_7}{a_8}} \]≤ 31 (1)
\[\overline {{a_4}{a_5}{a_6}{a_7}{a_8}} = \,{\left( {\overline {{a_7}{a_8}} } \right)^3}\]
⇔ 10000 ≤ \[{\left( {\overline {{a_7}{a_8}} } \right)^3}\]≤ 99999
⇔ 22 ≤ \[\overline {{a_7}{a_8}} \]≤ 46 (2)
Từ (1) và (2) suy ra: 22 ≤ \[\overline {{a_7}{a_8}} \]≤ 31
Lại có:
\[\overline {{a_4}{a_5}{a_6}{a_7}{a_8}} = \,{\left( {\overline {{a_7}{a_8}} } \right)^3}\]
⇔ \[\overline {{a_4}{a_5}{a_6}00} \, + \left( {\overline {{a_7}{a_8}} } \right)\, = \,{\left( {\overline {{a_7}{a_8}} } \right)^3}\]
⇔ \[\overline {{a_4}{a_5}{a_6}00} \, = \left( {\overline {{a_7}{a_8}} - 1} \right)\,\,\overline {{a_7}{a_8}} \left( {\overline {{a_7}{a_8}} + 1} \right)\]
Ta thấy: \[\overline {{a_4}{a_5}{a_6}00} \,\] chia hết cho 100 nên \[\left( {\overline {{a_7}{a_8}} - 1} \right)\,\,\overline {{a_7}{a_8}} \left( {\overline {{a_7}{a_8}} + 1} \right)\] chia hết cho 100. Mà \[\left( {\overline {{a_7}{a_8}} - 1} \right)\,\,\overline {{a_7}{a_8}} \left( {\overline {{a_7}{a_8}} + 1} \right)\]là 3 số tự nhiên liên tiếp nên để chia hết cho 100 thì khi và chỉ khi có 1 số chia hết cho 25.
Suy ra: \[\overline {{a_7}{a_8}} \] = 24 hoặc \[\overline {{a_7}{a_8}} \] = 25 hoặc \[\overline {{a_7}{a_8}} \] = 26
Với \[\overline {{a_7}{a_8}} \] = 24 ta có số: 57613824.
Với \[\overline {{a_7}{a_8}} \] = 25 ta có số: 62515625.
Với \[\overline {{a_7}{a_8}} \] = 26, không thỏa mãn.
Vậy số cần tìm là 57613824; 62515625.
Câu 15:
Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a chia hết 21, a chia hết 35 và a chia hết 99.
 Xem đáp án
Xem đáp án
Ta có:
a ∈ BCNN (21; 35; 99)
Ta có:
21 = 3 . 7
35 = 5 . 7
99 = 32 . 11
Suy ra: BCNN (21; 35; 99) = 32 . 5 . 7 . 11 = 3465.
Vì a nhỏ nhất khác 0 nên a = 3465.
Vậy a = 3465.
Câu 16:
Tìm số tự nhiên x sao cho 10 chia hết cho x – 1.
 Xem đáp án
Xem đáp án
Ta có: 10 chia hết cho x – 1
Suy ra: x – 1 là Ư(10) và x là số tự nhiên
Nên x – 1 ∈ {1; 2; 5; 10}
Vậy x ∈ {2; 3; 6; 11}.
Câu 17:
Chứng minh rằng: (xm + xn + 1) chia hết cho x2 + x + 1 khi và chỉ khi (mn – 2) chia hết cho 3.
 Xem đáp án
Xem đáp án
Đặt m = 3k + r với 0 ≤ r ≤ 2
n = 3t + s với 0 ≤ s ≤ 2
Ta có: xm + xn + 1
= x3k+r + x3t+s + 1
= x3kxr – xr + x3txs – xs + xr + xs + 1
= xr (x3k – 1) + xs (x3t – 1) + xr + xs + 1
Ta thấy: (x3k – 1) ⋮ (x2 + x + 1) và (x3t – 1) ⋮ (x2 + x + 1)
Vậy để (xm + xn + 1) ⋮ x2 + x + 1 thì (xr + xs + 1) ⋮ (x2 + x + 1) với 0 ≤ r, s ≤ 2
Hay khi: \[\left[ \begin{array}{l}r = 2;{\rm{ }}s = 1{\rm{ }}\\r = 1;{\rm{ }}s = 2\end{array} \right.\]
⇔\[\left[ \begin{array}{l}m{\rm{ }} = {\rm{ }}3k{\rm{ }} + {\rm{ }}2;{\rm{ }}n{\rm{ }} = {\rm{ }}3t{\rm{ }} + 1\\m{\rm{ }} = {\rm{ }}3k{\rm{ }} + {\rm{ }}1;{\rm{ }}n{\rm{ }} = {\rm{ }}3t{\rm{ }} + {\rm{ }}2\end{array} \right.\]
⇔\[\left[ \begin{array}{l}mn - 2 = \left( {3k + 2} \right)\left( {3t + 1} \right) - 2 = 9kt + 3k + 6t = 3\left( {3kt + k + 2t} \right)\\mn - 2 = \left( {3k + 1} \right)\left( {3t + 2} \right) - 2 = 9kt + 6k + 3t = 3\left( {3kt + 2k + t} \right)\end{array} \right.\]
Suy ra: mn – 2 ⋮ 3.
Câu 18:
Hai người đi bộ cùng chiều, cùng một lúc từ hai địa điểm A và B để đi đến điểm M cách A 12 km và cách B 9 km, với tốc độ lần lượt là 30 km/giờ và 10 km/giờ. Hai người gặp nhau tại đâu?
 Xem đáp án
Xem đáp án
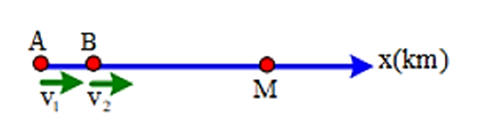
Chọn gốc thời gian và gốc tọa độ tại A, chiều dương từ A đến B
– Người đi từ A: x1 = v1t + x01
Với: v1 = 30 km/giờ; x01 = 0 → x1 = 30t
– Người đi từ B: x2 = v2t + x02
Với: v2 = 10 km/giờ; x02 = AB = MA − MB = 3 km → x2 = 10t + 3 (km)
– Hai người gặp nhau ta có: x1 = x2 → 30t = 10t + 3 → t = 0,15 (giờ)
⇒ x1 = x2 =4,5 km
Suy ra, hai người gặp nhau cách A 4,5 km và gặp nhau trước khi đến M.
Câu 19:
Tìm x, y thuộc ℕ biết: 36 – y2 = 8(x – 2010)2.
 Xem đáp án
Xem đáp án
Ta có: 36 – y2 = 8(x – 2010)2
⇒ y2 + 8(x–2010)2 = 36
Vì y2 ≥ 0 nên 8(x–2010)2 ≤ 36
Suy ra: (x–2010)2 ≤ \(\frac{{36}}{8}\)
Mặt khác: (x–2010)2 là số chính phương nên
\[\left[ \begin{array}{l}{\left( {x - 2010} \right)^2} = {\rm{ 0}}\\{\left( {x - 2010} \right)^2} = {\rm{ }}1\\{\left( {x - 2010} \right)^2} = {\rm{ }}4\end{array} \right.\]
Với (x–2010)2 = 0, ta có: y2 = 36. Suy ra y = 6 (vì y ∈ ℕ).
Với (x–2010)2 = 1, ta có: y2 = 28 (loại).
Với (x–2010)2 = 4, ta có: y2 = 4. Suy ra: y = 2 (vì y ∈ ℕ).
Vậy (x, y) = (2012; 2), (2008; 2), (2010; 6).
Câu 20:
Cho tam giác ABC, gọi A1, B1, C1 lần lượt là trung điểm của các cạnh BC, CA, AB. Đặt \(\overrightarrow {B{B_1}} = \overrightarrow u ;\,\,\overrightarrow {C{C_1}} = \overrightarrow v \). Tính \(\overrightarrow {BC} ;\overrightarrow {CA} ;\,\;\overrightarrow {AB} \) theo \(\overrightarrow u ;\overrightarrow v \).
 Xem đáp án
Xem đáp án
\[\overrightarrow {BC} = \overrightarrow {B{B_1}} + \overrightarrow {{B_1}{C_1}} + \overrightarrow {{C_1}C} = \overrightarrow u - \frac{1}{2}\overrightarrow {BC} - \overrightarrow v \]
Suy ra: \[\overrightarrow {BC} = \frac{2}{3}\overrightarrow u - \frac{2}{3}\overrightarrow v \]
Ta có: \[\overrightarrow {A{A_1}} + \overrightarrow {B{B_1}} + \overrightarrow {C{C_1}} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {CA} + \overrightarrow {CB} } \right) = \frac{1}{2}\left( {\overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 } \right) = 0\]
Suy ra: \[\overrightarrow {A{A_1}} = - \overrightarrow u - \overrightarrow v \]
\[\overrightarrow {CA} = \overrightarrow {C{A_1}} + \overrightarrow {{A_1}A} = \frac{{ - 1}}{2}BC - \overrightarrow {A{A_1}} = \frac{{ - 1}}{2}\left( {\frac{2}{3}\overrightarrow u - \frac{2}{3}\overrightarrow v } \right) + \overrightarrow u + \overrightarrow v = \frac{2}{3}\overrightarrow u + \frac{4}{3}\overrightarrow v \]
\[\overrightarrow {AB} = \overrightarrow {CB} - \overrightarrow {CA} = - \left( {\frac{2}{3}\overrightarrow u - \frac{2}{3}\overrightarrow v } \right) - \left( {\frac{2}{3}\overrightarrow u + \frac{4}{3}\overrightarrow v } \right) = \frac{{ - 4}}{3}\overrightarrow u - \frac{2}{3}\overrightarrow v \].
Câu 21:
Tìm các số tự nhiên n sao cho 3n + 7 chia hết cho n – 2 .
 Xem đáp án
Xem đáp án
Ta có: 3n + 7 = 3(n – 2) + 13
Để 3n + 7 chia hết cho n – 2 thì n – 2 thuộc Ư(13)
Vậy n – 2 = 1 hoặc n – 2 = 13 hay n = 3 hoặc n = 15.
Câu 22:
Giải phương trình: \(\frac{3}{{x - 3}} + \frac{5}{{x - 5}} + \frac{{17}}{{x - 17}} + \frac{{19}}{{x - 19}} = {x^2} - 11x - 4\).
 Xem đáp án
Xem đáp án
Điều kiện: x ≠ {3; 5; 17; 19}.
\(\frac{3}{{x - 3}} + \frac{5}{{x - 5}} + \frac{{17}}{{x - 17}} + \frac{{19}}{{x - 19}} = {x^2} - 11x - 4\)
⇔ \(\left( {\frac{x}{{x - 3}} - 1} \right) + \left( {\frac{x}{{x - 5}} - 1} \right) + \left( {\frac{x}{{x - 17}} - 1} \right) + \left( {\frac{x}{{x - 19}} - 1} \right) = x\left( {x - 11} \right)\)– 4
⇔ \(x\left( {\frac{1}{{x - 3}} + \frac{1}{{x - 5}} + \frac{1}{{x - 17}} + \frac{1}{{x - 19}}} \right) = x\left( {x - 11} \right)\)
⇔ \(2x\left( {x - 11} \right)\left( {\frac{1}{{\left( {x - 3} \right)\left( {x - 19} \right)}} + \frac{1}{{\left( {x - 5} \right)\left( {x - 17} \right)}}} \right) = x\left( {x - 11} \right)\)
\( \Leftrightarrow x\left( {x - 11} \right)\left[ {2\left( {\frac{1}{{{x^2} - 22x + 57}} + \frac{1}{{{x^2} - 22x + 85}}} \right) - 1} \right] = 0\)
TH1: x = 0 (t/m)
TH2: x – 11 = 0, suy ra x = 11 (t/m)
TH3: \(\frac{1}{{{x^2} - 22x + 57}} + \frac{1}{{{x^2} - 22x + 85}} = \frac{1}{2}\)
Đặt x2 – 22x + 57 = a
Ta có:
\(\frac{1}{a} + \frac{1}{{a + 28}} = \frac{1}{2}\)
⇔ a2 + 24a – 56= 0
⇔ \[\left[ \begin{array}{l}a = - 12 + 10\sqrt 2 \\a = - 12 - 10\sqrt 2 \end{array} \right.\]
⇔ \[\left[ \begin{array}{l}{x^2} - 22x + 69 - 10\sqrt 2 = 0\\{x^2} - 22x + 69 + 10\sqrt 2 = 0\end{array} \right.\]
⇔ \[x = 11 \pm \sqrt {52 \pm 10\sqrt 2 } \] (t/m).
Vậy x = 0, x = 11, \[x = 11 \pm \sqrt {52 \pm 10\sqrt 2 } \].
Câu 23:
Cho a – b = 10. Hãy tính A = (2a – 3b)2 + 2(2a – 3b)(3a – 2b) + (2b – 3a)2.
 Xem đáp án
Xem đáp án
A = (2a – 3b)2 + 2(2a – 3b)(3a – 2b) + (2b – 3a)2
A = (2a – 3b)2 + 2(2a – 3b)(3a – 2b) + (3a – 2b)2
A = [(2a – 3b) + (3a – 2b)]2
A = (5a – 5b)2
A = 52(a – b)2
A = 25 . 102
A = 2500.
Câu 24:
Khai triển đẳng thức sau: \({\left( {a + \frac{1}{a}} \right)^2}\).
 Xem đáp án
Xem đáp án
\({\left( {a + \frac{1}{a}} \right)^2} = {a^2} + 2.a.\frac{1}{a} + \frac{1}{{{a^2}}} = {a^2} + 2 + \frac{1}{{{a^2}}}\).
Câu 25:
Tìm x biết: \[\frac{{ - 4}}{{7x}} + \frac{7}{5} = \frac{{ - 1}}{8}:\left( { - 1 + \frac{2}{3}} \right)\].
 Xem đáp án
Xem đáp án
\[\frac{{ - 4}}{{7x}} + \frac{7}{5} = \frac{{ - 1}}{8}:\left( { - 1 + \frac{2}{3}} \right)\]
\[\frac{{ - 4}}{{7x}} + \frac{7}{5} = \frac{{ - 1}}{8}:\frac{{ - 1}}{3}\]
\[\frac{{ - 4}}{{7x}} + \frac{7}{5} = \frac{3}{8}\]
\[\frac{{ - 4}}{{7x}} = \frac{3}{8} - \frac{7}{5}\]
\[\frac{{ - 4}}{{7x}} = \frac{{ - 41}}{{40}}\]
x = \(\frac{{\left( { - 4} \right).40}}{{7.\left( { - 41} \right)}} = \frac{{160}}{{287}}\).
Câu 26:
Chứng minh rằng với mọi n ∈ ℕ* ta có 11n+1 + 122n–1 chia hết cho 133.
 Xem đáp án
Xem đáp án
Đặt An = 11n+1 + 122n–1
A1 = 112 + 12 = 133 chia hết cho 133
Giả sử Ak = 11k+1 + 122k–1 đã chia hết cho 133
Xét: Ak+1 = 11k+2 + 122k+1
= 11 . 11k+1 + 122 . 122k–1
= 11. 11k+1 + 122k–1 (11 + 133)
= 11 . Ak + 133 . 122k–1
Vì Ak chia hết cho 133 và 133 . 122k–1 chia hết cho 133 nên Ak+1 chia hết cho 133.
Vậy điều giả sử là đúng.
Câu 27:
Chứng minh rằng A = 7 + 72 + 73 +.. + 7100 chia hết cho 50.
 Xem đáp án
Xem đáp án
Ta có:
A = 7 + 72 + 73 +.. + 7100
A = (7 + 72 + 73 + 74) + (75 + 76 + 77 + 78) + (797 + 798 + 799 + 7100)
A = (7 + 72 + 73 + 74) . (1 + 74 + 78 + … + 796)
Ta thấy 7 + 72 + 73 + 74 = 2800 = 50 . 56 chia hết cho 50
Vì vậy A chia hết cho 50.
Câu 28:
Thu gọn tổng sau A = 2 + 22 + 23 + … + 2100.
 Xem đáp án
Xem đáp án
Ta có: 2A = 22 + 23 + … + 2101
2A – A = (22 + 23 + … + 2101) – (2 + 22 + 23 + … + 2100)
A = 2101 – 2
Câu 29:
Cho hình bình hành ABCD, kẻ AH, CK vuông góc với BD. Chứng minh rằng AHCK là hình bình hành.
 Xem đáp án
Xem đáp án
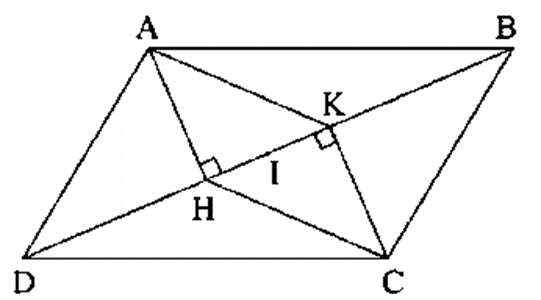
Do ABCD là hình bình hành nên AD // BC và AD = BC.
Do AD // BC nên \(\widehat {ADB} = \widehat {CBD}\) (so le trong)
Xét ∆ADH và ∆CBK có:
\(\widehat {AHD} = \widehat {CKB}\)= 90°
AD = BC (chứng minh trên);
\(\widehat {ADH} = \widehat {CBK}\)(do \(\widehat {ADB} = \widehat {CBD}\))
Do đó ∆ADH = ∆CBK (cạnh huyền – góc nhọn).
Suy ra AH = CK (hai cạnh tương ứng).
Ta có AH ⊥ DB và CK ⊥ DB nên AH // CK.
Tứ giác AHCK có AH // CK và AH = CK nên AHCK là hình bình hành.
Câu 30:
Cho các điểm A(1; – 2), B(– 2; 3) và C(0; 4). Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
\(\left\{ \begin{array}{l}\overrightarrow {AB} = \left( { - 3;5} \right)\\\overrightarrow {BC} = \left( {2;1} \right)\\\overrightarrow {CA} = \left( {1; - 6} \right)\end{array} \right.\)⇒ \(\left\{ \begin{array}{l}AB = \sqrt {{{\left( { - 3} \right)}^2} + {5^2}} = \sqrt {34} \\BC = \sqrt {{2^2} + {1^2}} = \sqrt 5 \\CA = \sqrt {{1^2} + {{\left( { - 6} \right)}^2}} = \sqrt {37} \end{array} \right.\)
Nửa chu vi tam giác ABC là: p = \(\frac{{AB + BC + CA}}{2} = \frac{{\sqrt {34} + \sqrt 5 + \sqrt {37} }}{2}\)
Áp dụng công thức Hê – rông ta có:
SABC = \(\sqrt {p\left( {p - AB} \right)\left( {p - BC} \right)\left( {p - CA} \right)} \)
=\(\sqrt {\frac{{\sqrt {34} + \sqrt 5 + \sqrt {37} }}{2}\left( {\frac{{\sqrt {34} + \sqrt 5 - \sqrt {37} }}{2}} \right)\left( {\frac{{\sqrt {37} + \sqrt 5 - \sqrt {34} }}{2}} \right)\left( {\frac{{\sqrt {37} - \sqrt 5 + \sqrt {34} }}{2}} \right)} \)
= \[\frac{{\sqrt {\left[ {{{\left( {\sqrt {34} + \sqrt 5 } \right)}^2} - 37} \right]\left[ {37 - {{\left( {\sqrt 5 - 34} \right)}^2}} \right]} }}{4}\]
= \[\frac{{\sqrt {\left( {34 + 2\sqrt {170} + 5 - 37} \right)\left( {37 - 5 + 2\sqrt {170} - 34} \right)} }}{4}\]
= \[\frac{{\sqrt {\left( {2 + 2\sqrt {170} } \right)\left( {2\sqrt {170} - 2} \right)} }}{4}\]
= \[\frac{{\sqrt {4.170 - 4} }}{4}\]
= \[\frac{{\sqrt {169} }}{2}\]
= \[\frac{{13}}{2}\].
Câu 31:
Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của AD và BC. Đường chéo AC cắt các đoạn thẳng BE và DF theo thứ tự tại P và Q.
a) Chứng minh tứ giác BEDF là hình bình hành.
b) Chứng minh AP = PQ = QC.
c) Gọi R là trung điểm của BP. Chứng minh tứ giác ARQE là hình bình hành.
 Xem đáp án
Xem đáp án
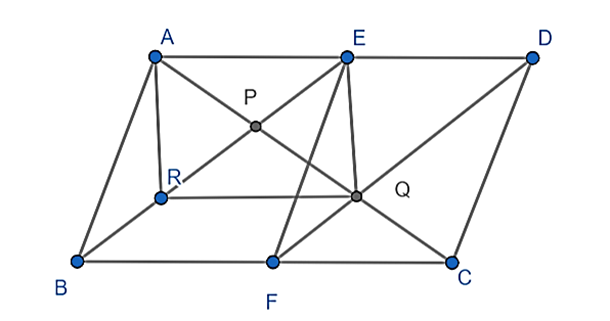
a) Ta có: ED = \(\frac{1}{2}AD\)
BF = \(\frac{1}{2}BC\)
Mà ABCD là hình bình hành nên AD = BC và AD// BC
Suy ra: ED = BF và ED // BF
Vậy EDFB là hình bình hành.
b) Vì EB // DF nên EP // DQ
Xét tam giác ADQ có:
EP // DQ và E là trung điểm AD nên PE là đường trung bình của tam giác ADQ.
Suy ra: P là trung điểm AQ hay AP = PQ (1)
Xét tam giác BPC có:
FQ // BP và F là trung điểm BC nên FQ là đường trung bình của tam giác BPC.
Suy ra: Q là trung điểm của PC hay PQ = QC (2)
Từ (1) và (2) suy ra: AP = PQ = QC.
c) Do AE // BC nên áp dụng định lí Thalès ta có:
\(\frac{{AP}}{{PC}} = \frac{{EP}}{{PB}} = \frac{1}{2}\)
Mặt khác R là trung điểm PB nên PR = RB = \(\frac{1}{2}PB\)
Suy ra: EP = PR = RB = \(\frac{1}{2}PB\)
Xét tứ giác ARQE có:
AP = PQ và PE = PR (2 đường chéo AQ, RE cắt nhau tại trung điểm mỗi đường)
Vậy tứ giác ARQE là hình bình hành.
Câu 32:
Cho p và 2p + 1 là các số nguyên tố ( p > 5 ). Hỏi 4p + 1 là số nguyên tố hay hợp số?
 Xem đáp án
Xem đáp án
Xét 3 số tự nhiên tiếp : 4p, 4p + 1, 4p + 2 .
Tích của ba số tự nhiên liên tiếp chia hết cho 3 nên trong 3 số này có một số chia hết cho 3 (1)
Ta xét :
+ Vì p là số nguyên tố ( p > 5 ) nên p không chia hết cho 3 .
Do vậy 4p không chia hết cho 3 (2)
+ Vì 2p + 1 là số nguyên tố và p > 5 nên 2p + 1 > 3.
Suy ra 2p + 1 không chia hết cho 3 .
Mà 4p + 2 = 2(2p + 1) ⇒ 4p + 2 không chia hết cho 3 (3)
Từ (1) , (2) , (3) ta suy ra được 4p + 1 chia hết cho 3 .
Mà p > 5 ⇒ 4p + 1 > 3 không thể là số nguyên tố .
Hay nói cách khác 4p + 1 là hợp số.
Câu 33:
Cho tam giác ABC vuông tại B. M là trung điểm AC. Kẻ MH vuông góc với BC, kẻ MI vuông góc với AB. Chứng minh BIMH là hình chữ nhật.
 Xem đáp án
Xem đáp án
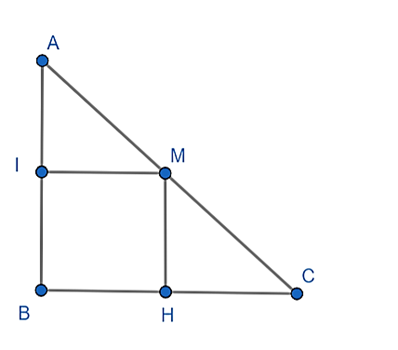
Ta có:
MH ⊥ BC nên \(\widehat {MHB}\)= 90°
AB ⊥ BC nên \(\widehat {IBH}\)= 90°
MI ⊥ AB nên \(\widehat {BIM}\)= 90°
Xét tứ giác BIMH có:
\(\widehat {MHB}\)=\(\widehat {IBH}\)= \(\widehat {BIM}\)= 90°
Suy ra: BIMH là hình chữ nhật.
Câu 34:
Cho tam giác ABC vuông tại A có đường cao AH, M là một điểm di động trên cạnh BC. Gọi I là hình chiếu của M trên AB. Trên cạnh AC lấy điểm K sao cho IK = AM. Chứng minh tứ giác AIMK là hình chữ nhật.
 Xem đáp án
Xem đáp án
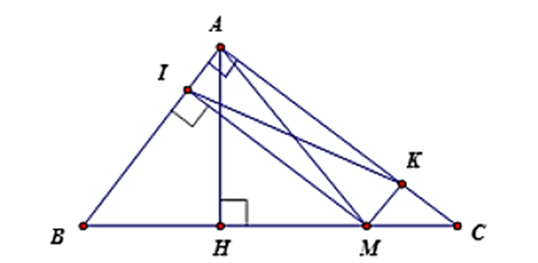
Xét ∆AMI và ∆AKI có:
AI chung
\(\widehat A = \widehat I\)= 90°
IK=AM
Suy ra: ΔAMI = ΔAKI (cạnh huyền cạnh góc vuông)
⇒ AK = IM
Xét tứ giác AIMK: \(\widehat A = \widehat I\)= 90°
Suy ra: AK // IM
Mà AK = IM nên AIMK là hình bình hình.
Mặt khác \(\widehat A = \widehat I\)= 90° nên AIMK là hình chữ nhật.
Câu 35:
Cho x, y thỏa mãn: \(\left( {x + \sqrt {{x^2} + 2022} } \right)\left( {y + \sqrt {{y^2} + 2022} } \right) = 2022\). Tính x + y?
 Xem đáp án
Xem đáp án
\(\left( {x + \sqrt {{x^2} + 2022} } \right)\left( {y + \sqrt {{y^2} + 2022} } \right) = 2022\)
Mà \(\left( {x + \sqrt {{x^2} + 2022} } \right)\left( {\sqrt {{x^2} + 2022} - x} \right) = 2022\)
Nên \(\sqrt {{x^2} + 2022} - x = y + \sqrt {{y^2} + 2022} \)
Hay \(x + y = \sqrt {{x^2} + 2022} - \sqrt {{y^2} + 2022} \)(1)
Lại có:
\(\left( {y + \sqrt {{y^2} + 2022} } \right)\left( {\sqrt {{y^2} + 2022} - y} \right) = 2022\)
Nên \(x + y = \sqrt {{y^2} + 2022} - \sqrt {{x^2} + 2022} \)(2)
Từ (1) và (2) ta có:
2(x + y) = 0
Suy ra: x + y = 0.
Câu 36:
 Xem đáp án
Xem đáp án
3 (22 + 1) (24 + 1) (28 + 1) (216 + 1)
= (22 – 1) (22 + 1) (24 + 1) (28 + 1) (216 + 1)
= (24 – 1)( (24 + 1) (28 + 1) (216 + 1)
= (28 – 1) (28 + 1) (216 + 1)
= (216 – 1) (216 + 1)
= 232 – 1.
Câu 37:
 Xem đáp án
Xem đáp án
Ta có: 2021 = 2 + 2019
Vì 2019 có tổng các chữ số là 2 + 0 + 1 + 9 = 12 ⁝ 3 nên 2019 ⁝ 3 vì thế 2019 không phải là số nguyên tố.
Ngoài số 2 là số chẵn nguyên tố duy nhất, các số nguyên tố khác hai đều là số lẻ.
Do vậy tổng của hai số nguyên tố khác 2 là một số chẵn.
Mà 2021 là số lẻ
Vậy 2021 không thể viết thành tổng của hai số nguyên tố được.
Câu 38:
Hai người thợ nếu làm chung 1 công việc thì sau 5 giờ sẽ xong. Nhưng sau khi cùng làm được 3 giờ thì người thợ cả có việc bận nghỉ làm. Người thợ thứ 2 làm nốt chỗ công việc còn lại mất 6 giờ mới xong. Hỏi nếu mỗi người làm một mình chỗ công việc đó thì phải mất bao nhiêu thời gian?
 Xem đáp án
Xem đáp án
Trong 1 giờ, cả hai người làm được là:
1 : 5 = \(\frac{1}{5}\) (giờ)
Giả sử hai người đều làm trong 3 giờ thì hai người làm được là:
\(\frac{1}{5}\) . 3 = \(\frac{3}{5}\) (công việc)
Số phần công việc hai người còn lại làm được là:
1 – \(\frac{3}{5}\)= \(\frac{2}{5}\) (công việc)
Nếu 1 mình người thứ hai làm thì xong trong :
6 : \(\frac{2}{5}\)= 15 (giờ)
Một mình người thứ nhất làm thì xong được là :
1 : (\(\frac{1}{5}\) – \(\frac{1}{{15}}\)) = \(\frac{{15}}{2}\)= 7,5 ( giờ )
Đáp số: Người thứ hai: 15 giờ; người thứ nhất: 7,5 giờ.
Câu 39:
Chứng minh rằng trong tam giác ABC ta có hệ thức: sin A = sinB. cosC + sinC. cosB.
 Xem đáp án
Xem đáp án
Theo định lí tổng ba góc của tam giác ta có:
\(\widehat A + \widehat B + \widehat C\)= 180°
⇒ \(\widehat A\)= 180° – \(\left( {\widehat B + \widehat C} \right)\)
sin A = sin \(\left[ {180^\circ {\rm{ }} - \,\left( {\widehat B + \widehat C} \right)} \right]\)= sin (B + C) = sin B. cos C + sin C. cos B.
Câu 40:
Một trường học bán trú chuẩn bị số gạo cho 80 học sinh ăn trong 20 ngày. Sau khi ăn hết một nửa số gạo đó trường học có thêm một số học sinh mới nên số gạo còn lại chỉ đủ cho ăn trong 5 ngày nữa. Hỏi trường đó thêm bao nhiêu học sinh nữa?
 Xem đáp án
Xem đáp án
Coi số gạo mỗi học sinh ăn trong một ngày là một suất gạo.
Số ngày còn lại là:
20 – 5 =15 (ngày)
Số học sinh ăn hết số gạo trong 5 ngày là:
(80 . 15) : 5 = 240 (học sinh)
Trường đó có thêm số học sinh là:
240 – 80 = 160 (học sinh).
Đáp số: 160 học sinh.
Câu 41:
Một khu vườn hình chữ nhật có chiều dài 250 m, chiều rộng 200 m.Người ta dùng \(\frac{1}{5}\) diện tích của vườn để trồng cam, \[\frac{3}{4}\] diện tích còn lại để trồng bưởi. Diện tích còn lại sau khi đã trồng cam và bưởi để trồng cây cảnh.Tính diện tích rồng cây cảnh?
 Xem đáp án
Xem đáp án
Diện tích khu vườn là hình chữ nhật là:
250 . 200 = 50000 (m2)
Diện tích trồng cam là:
50000. \(\frac{1}{5}\) = 10000 (m2)
Diện tích trồng bưởi là:
(50000 – 10000) . \[\frac{3}{4}\] = 30000 (m2)
Diện tích trồng cây cảnh là:
50000 – 30000 – 10000 = 10000 (m2)
Đáp số: 10000 m2.
Câu 42:
Một khu đất hình chữ nhật được quy hoạch thành khu đô thị có chiều dài 0,5km, chiều rộng bằng \(\frac{5}{8}\) chiều dài. Tính diện tích khu đất đó với đơn vị là mét vuông, là héc–ta.
 Xem đáp án
Xem đáp án
Đổi 0,5 km = 500 m
Chiều rộng khu đất là:
500 . \(\frac{5}{8}\)= \(\frac{{625}}{2}\)(m)
Diện tích khu đất theo mét vuông là:
500 . \(\frac{{625}}{2}\)= 156250 (m2)
Đổi 156250 m2 = 15,625 ha.
Câu 43:
Một mảnh đất hình chữ nhật có nửa chu vi là 30m. Chiều dài hơn chiều rộng 16m. Tính diện tích hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Chiều dài hình chữ nhật là:
(30 + 16) : 2 = 23 (m)
Chiều rộng của hình chữ nhật là:
30 – 23 = 7 (m)
Diện tích hình chữ nhật là:
7 . 23 = 161 (m2)
Đáp số: 161 m2.
Câu 44:
Một người bán hàng vải, lần thứ nhất bán được \(\frac{1}{2}\) số vải, lần thứ hai bán \(\frac{1}{3}\) số vải còn lại và 7m. Hỏi tấm vải đó dài bao nhiêu m?
 Xem đáp án
Xem đáp án
Số phần vải sau hai lần đầu người đó bán được là:
\(\frac{1}{2}\) + \(\frac{1}{3}\) = \(\frac{5}{6}\) (phần)
số phần vải tương đương với 7m vải là:
1 – \(\frac{5}{6}\) = \(\frac{1}{6}\) (phần)
Vậy độ dài tấm vải đó là:
7 : \(\frac{1}{6}\) = 42 (m)
Đáp số: 42 m.
Câu 45:
Một người dùng hết bể nước trong 18 ngày. Nếu con đến ở chung thì 2 người dùng hết trong 10 ngày. Hỏi nếu người con dùng riêng thì hết trong bao nhiêu ngày (lượng nước mỗi người dùng trong 1 ngày là như nhau)?
 Xem đáp án
Xem đáp án
Người đó dùng trong 1 ngày hết là :
1 : 18 = \(\frac{1}{{18}}\) (bể)
Cả hai người dùng trong 1 ngày hết là :
1 : 10 = \(\frac{1}{{10}}\) (bể)
Người con dùng trong 1 ngày cần là :
\[\frac{1}{{10}} - \frac{1}{{18}} = \frac{2}{{45}}\] (bể)
Nếu riêng người con thì dùng hết trong số ngày là:
1 : \(\frac{2}{{45}}\) = \(\frac{{45}}{2}\) = 22,5 (ngày)
Đáp số: 22,5 ngày.
Câu 46:
Một người đi hết quãng đường 8km hết 20 phút. Một người khác trong 2 giờ đi được quãng đường 45km . Hỏi ai là người đi nhanh hơn?
 Xem đáp án
Xem đáp án
Đổi 20 phút = \(\frac{1}{3}\)giờ
Vận tốc của người thứ nhất là:
8 : \(\frac{1}{3}\) = 24 (km/giờ)
Vận tốc của người thứ hai là:
45 : 2 = 22,5 (km/giờ)
Vậy người thứ nhất đi nhanh hơn người thứ hai.
Câu 47:
Một sân chơi có hình chữ nhật với chiều dài 12m và chiều rộng 8m.
a) Tính chu vi và diện tích sân chơi đó.
b) Người ta dùng các viên gạch hình vuông có chiều dài cạnh là 40cm để lát nền cho sân chơi. Hỏi cần dùng bao nhiêu viên gạch để lát kín nền sân chơi?
c) Biết mỗi viên gạch giá 25000 đồng và công lát nền là 15000 đồng/m2. Tính tổng số tiền phải chi ra để lát nền cho sân chơi?
 Xem đáp án
Xem đáp án
a) Chu vi sân chơi đó là:
(12 + 8) . 2 = 40 (m).
Diện tích sân chơi đó là:
12 . 8 = 96 (m2).
b) Đổi 40 cm = 0,4 m
Diện tích một viên gạch là:
0,4 . 0,4 = 0,16 (m2).
Số viên gạch cần là:
96 : 0,16 = 600 (viên gạch ).
c) Số tiền để trả 600 viên gạch là:
600 . 25000 = 15000000 (đồng).
Công lát sân chơi đó:
96 . 15000 = 1440000 (đồng).
Tổng số tiền để chi cho việc lát nền là:
15000000 + 1440000 = 16440000 (đồng).
Câu 48:
Một thửa ruộng hình chữ nhật có chu vi bằng 0,56 km chiều rộng bằng \(\frac{1}{3}\) chiều dài
a) Tính diện tích thửa ruộng đó
b) Biết rằng trung bình cứ 100m2 thu hoạch được 20 kg Hỏi trên cả thửa ruộng đó người ta thu hoạch được bao nhiêu kg ngô?
 Xem đáp án
Xem đáp án
a) Nửa chu vi của thửa ruộng là :
0,56 : 2 = 0,28 (km)
Chiều dài thửa ruộng là là :
(0,28 : 4) × 3 = 0,21 (km)
Chiều rộng thửa ruộng là :
0,28 – 0,21 = 0,07 (km)
Diện tích thửa ruộng là :
0,21 . 0,07 = 0,0147 (km2) = 14700 m2.
b) Trên cả thửa ruộng đó người ta thu hoạch được số kg ngô là:
14700 : 100 . 20 = 2940 (kg).
Câu 49:
Người ta cấy lúa trên một thửa ruộng hình chữ nhật có chiều dài 120 m, chiều rộng bằng \[\frac{2}{3}\]chiều dài. Trung bình 150 m2 thu hoạch dược 60 kg lúa. Hỏi thửa ruộng đó thu được bao nhiêu tạ lúa ?
 Xem đáp án
Xem đáp án
Chiều rộng thửa ruộng đó là:
120 : 3 . 2 = 80 (m)
Diện tích của thửa ruộng là:
120 . 80 = 9600 (m2)
Thửa ruộng đó thu được số kg lúa là :
9600 : 150 . 60 = 3840 (kg)
Đổi 3840 kg = 38,4 tạ.
Đáp số: 38,4 tạ lúa.
Câu 50:
Mảnh vườn hình chữ nhật có chiều rộng bằng 4 cm và diện tích bằng 160 cm2.
a) Tính chu vi mảnh vườn hình chữ nhật?
b) Người ta dự định trồng cây xung quanh vườn sao cho mỗi góc vườn có một cây, khoảng cách giữa hai cây là 4cm . Tính số cây cần để trồng?
 Xem đáp án
Xem đáp án
a) Chiều dài mảnh vườn là:
160 : 4 = 40 (cm).
Chu vi mảnh vườn là:
(40 + 4) . 2 = 88 (cm).
b) Do khoảng cách giữa hai cây là 4 cm nên trên mỗi chiều rộng ta trồng được 2 cây và cây này nằm ở góc của mảnh vườn nên nó cũng nằm trên chiều dài của vườn.
Trên mỗi chiều dài ta trồng được số cây là:
40 : 4 = 10 (cây).
Tổng số cây trồng được là:
10 + 10 = 20 (cây).
Câu 51:
Tìm tất cả số nguyên tố sao cho nó vừa là tổng vừa là hiệu của hai số nguyên tố.
 Xem đáp án
Xem đáp án
Trường hợp 1: p chẵn
Vì p là số nguyên tố chẵn nên nó chỉ có thể là 2, nhưng 2 không thể là tổng 2 số nguyên tố vì 2 là số nguyên tố nhỏ nhất .
⇒ p không tồn tại
Trường hợp 2: p lẻ
Giả sử p = m + n ( m,n là số nguyên tố ). Mà p lẻ ⇒ trong m và n có 1 lẻ, 1 chẵn
Nếu m là số lẻ, n là số chẵn ⇒ n = 2 ⇒ p = m + 2 ⇒ m = p – 2 (1)
Tương tự, p = q – r ( q, r là số nguyên tố ).
Vì p là số lẻ ⇒ trong q và r có 1 lẻ, 1 chẵn
Xét q chẵn ⇒ q = 2 ⇒ p = 2 – r < 0 ( loại )
Vậy q là số lẻ , r là số chẵn ⇒ r = 2 ⇒ p = q – 2 ⇒ q = p + 2 (2)
Từ (1) , (2) ta thấy p – 2 ; p ; p + 2 là 3 số nguyên tố lẻ (3)
+ Nếu p < 5 ⇒ p – 2 < 3 ⇒ p – 2 không thể là số nguyên tố lẻ
+ Nếu p = 5 ⇒ (3) thỏa mãn ⇒ p = 5 .
+ Nếu p > 5 ⇒ p – 2 ; p ; p + 2 đều lớn hơn 3
+ Nếu p – 2 chia 3 dư 1 thì p chia hết cho 3 ⇒ p không phải số nguyên tố (loại)
+ Nếu p–2 chia 3 dư 2 thì p + 2 chia hết cho 3 ⇒ p + 2 ko phải số nguyên tố (loại)
⇒ p chỉ có thể là 5
Vậy p = 5.
Câu 52:
Tìm các số nguyên dương m, n biết: 2m + 2n = 2m+n.
 Xem đáp án
Xem đáp án
Ta có:
2m + 2n = 2m+n
⇔ 2m + 2n = 2m.2n
⇔ 2m + 2n – 2m.2n = 0
⇔ 2m (2n – 1) – (2n –1) = 1
⇔ (2m – 1)(2n – 1) = 1 = 1 . 1
Suy ra:
\(\left\{ \begin{array}{l}{2^m} - 1 = 1\\{2^n} - 1 = 1\end{array} \right.\) ⇒ \(\left\{ \begin{array}{l}m = 1\\n = 1\end{array} \right.\)
Vậy m = n = 1.
Câu 53:
Tìm số tự nhiên nhỏ nhất khác 0 biết rằng a chia hết cho 15; a chia hết cho 18.
 Xem đáp án
Xem đáp án
Ta có: a ∈ BCNN (15; 18)
15 = 3 . 5
18 = 2 . 32
Suy ra: BCNN (21; 35; 99) = 2 . 32 . 5 = 90
Vì a là số tự nhiên nhỏ nhất khác 0 nên a = 90.
Câu 54:
Tìm số tự nhiên x biết 36 chia hết cho x + 5.
 Xem đáp án
Xem đáp án
Theo bài ra ta có:
36 ⋮ (x + 5)
Suy ra: x + 5 ∈ Ư(36)
Vì x là số tự nhiên nên x + 5 ∈ {1; 2; 3; 4; 6; 9; 12; 18; 36}
⇒ x ∈ {–4; –3; –2; –1; 1; 4; 7; 13; 21} mà x thuộc ℕ.
Vậy x ∈{1; 4; 7; 13; 21}.
Câu 55:
 Xem đáp án
Xem đáp án
Số lẻ lớn nhất có 3 chữ số là 999
Số lẻ nhỏ nhất có 3 chữ số là 101
Số các số hạng của dãy các số lẻ có 3 chữ số là:
(999 – 101) : 2 + 1 = 450
Tổng các số lẻ có 3 chữ số là:
(999 + 101) . 450 : 2 = 247500
Trung bình cộng của các số lẻ có 3 chữ số là:
247500 : 450 = 550.
Câu 56:
Tổng hai số là 724. Tìm số lớn biết rằng khi xóa chữ số 7 ở hàng trăm của số lớn thì ta được số bé.
 Xem đáp án
Xem đáp án
Khi xoá đi chữ số 7 ở hàng trăm tức là số đó giảm đi 700 đơn vị.
Suy ra 700 là hiệu giữa số lớn và số bé.
Số lớn là:
(724 + 700) : 2 = 712.
Câu 57:
Tìm x biết: \(\left( {x - \frac{3}{2}} \right)\left( {2x + 1} \right) > 0\).
 Xem đáp án
Xem đáp án
\(\left( {x - \frac{3}{2}} \right)\left( {2x + 1} \right) > 0\)
⇔ \(\left[ \begin{array}{l}\left\{ \begin{array}{l}x - \frac{3}{2} > 0\\2x + 1 > 0\end{array} \right.\\\left\{ \begin{array}{l}x - \frac{3}{2} < 0\\2x + 1 < 0\end{array} \right.\end{array} \right.\)
⇔ \(\left[ \begin{array}{l}x > \frac{3}{2}\\x < \frac{{ - 1}}{2}\end{array} \right.\).
Câu 58:
Hỏi nếu bán kính 1 hình tròn giảm đi 20% thì diện tích hình tròn giảm đi bao nhiêu %?
 Xem đáp án
Xem đáp án
Khi giảm bán kính của hình tròn đi 20% thì bán kính của hình trong khi đó là:
100% – 20% = 80%
Diện tích hình tròn mới là:
80% . 80% = 64%
Diện tích hình tròn mới so với ban đầu giảm đi:
100% – 64% = 36%
Vậy nếu giảm bán kình 20% thì diện tích giảm 36%.
Câu 59:
Cho tam giác ABC. Gọi D, M, E theo thứ tự là trung điểm của AB, BC, CA.
a) Chứng minh tứ giác ADME là hình bình hành.
b) Nếu tam giác ABC cân tại A thì tứ giác ADME là hình gì? Vì sao?
c) Nếu tam giác ABC vuông tại A thì tứ giác ADME là hình gì? Vì sao?
d) Trong trường hợp tam giác ABC vuông tại A, cho biết AB = 6 cm, AC = 8 cm. Tính AM.
 Xem đáp án
Xem đáp án
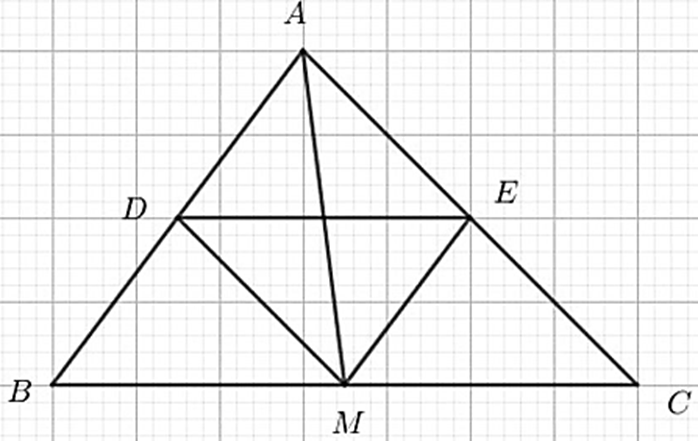
a) Ta có: EM là đường trung bình của tam giác ABC
Suy ra: EM // AB và EM = \(\frac{1}{2}AB\)= AD
Xét tứ giác ADME có: AD // ME và AD = ME
Suy ra tứ giác ADME là hình bình hành.
b) Nếu tam giác ABC cân tại A thì AE = AD = \(\frac{1}{2}AB\)=\(\frac{1}{2}AC\)
Suy ra: ADME là hình thoi vì AD = AE = ME = MD
c) Nếu tam giác ABC vuông tại A thì \(\widehat {EAD}\) = 90°
Suy ra: ADME là hình chữ nhật.
d) Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
BC = \(\sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + 8{}^2} = 10\)(cm)
Vì tam giác ABC vuông tại A nên đường trung tuyến bằng nửa cạnh huyền hay
AM = \(\frac{1}{2}BC\)= 5(cm).
Câu 60:
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB và D là điểm đối xứng của M qua I. Chứng minh rằng: AD // BM và tứ giác ADBM là hình thoi.
 Xem đáp án
Xem đáp án
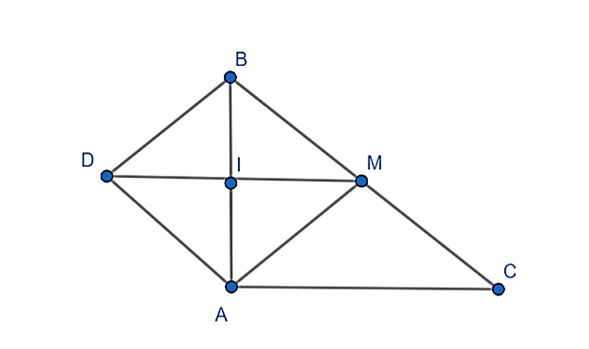
Ta có: ID = IM (D là điểm đối xứng của M qua I)
IA = IB (I là trung điểm AB)
Suy ra: tứ giác ADBM là hình bình hành (2 đường chéo đi qua trung điểm mỗi đường) (1)
Do đó: AD // BM.
Lại có:
IM là đường trung bình của tam giác ABC ⇒ IM // AC
Mà AB ⊥ AC
⇒ IM ⊥ AB hay DM ⊥ AB (2)
Từ (1) và (2) suy ra: ADBM là hình thoi.
Câu 61:
Gọi S là tập hợp tất cả các số tự nhiên là ước của số A = 22 . 33 . 5. Hỏi tập S có bao nhiêu phần tử?
 Xem đáp án
Xem đáp án
Số các ước của A là: 3 . 4 . 2 = 24
Vậy S có 24 phần tử.
Câu 62:
Một thửa ruộng hình chữ nhật có chiều dài 140 m, chiều rộng bằng 0,75 lần chiều dài. Trên thửa ruộng người ta trồng lúa, trung bình cứ 100 m2 thu hoạch được 50 kg thóc. Hỏi trên thửa ruộng đó người ta thu hoạch được bao nhiêu tấn thóc ?
 Xem đáp án
Xem đáp án
Chiều rộng thửa ruộng là:
140 . 0,75 = 105 (m)
Diện tích thửa ruộng là:
140 . 105 = 14700 (m2).
Trên thửa ruộng đó người ta thu hoạch được số tấn thóc là:
14700 : 100 . 50 = 7350 (kg)
Đổi 7350 kg = 7,35 tấn.
Vậy thu hoạch được 7,35 tấn thóc.
Câu 63:
Một chiếc điện thoại sau khi hạ giá hai lần, mỗi lần giảm 10% giá đang bán thì có giá bán là 1215000 đồng. Tính giá tiền của chiếc điện thoại đó.
 Xem đáp án
Xem đáp án
Giá lần đầu tiên là 100%.
Giảm lần thứ nhất 10% thì còn 90%.
Giảm 10% lần 2 thì giảm: 90% : 10% = 9%
1215000 đồng ứng với:
100% – 10% – 9% = 81% (giá lần đầu tiên)
Giá tiền của chiếc điện thoại đó là:
1215000 : 81 . 100 = 1500000 ( đồng )
Câu 64:
Một người có số gạo nếp bằng 75% số gạo tẻ. Sau khi bán 6 kg gạo nếp thì số gạo nếp còn lại bằng 60% số gạo tẻ. Hỏi lúc đầu người đó có tất cả bao nhiêu kg gạo?
 Xem đáp án
Xem đáp án
6kg gạo nếp bằng:
75 – 60 = 15% (gạo tẻ)
Số gạo tẻ là:
6 : 15 . 100 = 40 (kg)
Số gạo nếp lúc đầu là:
40 : 100 . 75 = 30 (kg)
Lúc đầu có tất cả số kg gạo là:
40 + 30 = 70 (kg)
Câu 65:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC. Chứng minh: \[\frac{{A{B^3}}}{{CN}} = \frac{{A{C^3}}}{{BM}}\].
 Xem đáp án
Xem đáp án
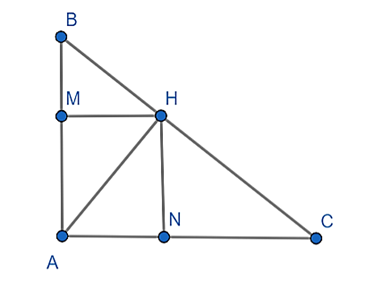
Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
AB2 = BH.BC ⇒ AB4 = BH2.BC2
AC2 = CH.BC ⇒ AC4 = CH2.BC2
\[\frac{{A{B^4}}}{{A{C^4}{\rm{ }}}} = \frac{{B{H^2}.B{C^2}}}{{C{H^2}.B{C^2}}} = \frac{{B{H^2}}}{{C{H^2}}} = \frac{{BM.AB}}{{CN.AC}}\]
Suy ra: \[\frac{{A{B^3}}}{{A{C^3}{\rm{ }}}} = \frac{{BM}}{{CN}}\,\,\,\]hay \[\frac{{A{B^3}}}{{CN}} = \frac{{A{C^3}}}{{BM}}\].
Câu 66:
Viết số tự nhiên nhỏ nhất có bốn chữ số khác nhau và đều là số lẻ.
 Xem đáp án
Xem đáp án
Một số có bốn chữ số khác nhau và đều là số lẻ là số nhỏ nhất thì:
Chữ số lẻ đầu tiên của nó phải là số nhỏ nhất khác 0 là số 1
Chữ số lẻ kế tiếp phải là số nhỏ nhất khác 1 tức là số 3
Chữ số lẻ kế tiếp phải là số nhỏ nhất khác 1 và 3 tức là số 5
Chữ số lẻ hàng đơn vị phải nhỏ nhất khác 1,3,5 tức là số 7
Vậy số tự nhiên nhỏ nhất có bốn chữ số khác nhau và đều là số lẻ: 1357.
Câu 67:
 Xem đáp án
Xem đáp án
Với n = 0, 2n + 2023 = 2024 (loại vì không phải số chính phương)
Với n = 1, 2n + 2023 = 2025 = 452
Với n ≥ 2 thì 2n chia hết cho 4
2n + 2023 = 2n + 4 . 505 + 3
Khi đó: 2n + 2023 chia 4 dư 3
Suy ra 2n + 2023 không phải số chính phương vì số chính phương chia hết cho 4 hoặc chia 4 dư 1)
Vậy n = 1.
Câu 68:
Cho hình chữ nhật có chu vi 324 m. Nếu ta tăng chiều dài thêm 5 m và chiều rộng thêm 3 m thì chiều dài gấp 3 lần chiều rộng.Tính diện tích hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Nửa chu vi hình chữ nhật là:
324 : 2 = 162 (m)
Nửa chu vi lúc sau là:
162 + (5 + 3) = 170 (m)
Chiều rộng là:
170 : (1 + 4)= 34 (m)
Chiều dài là:
170 – 34 = 136 (m)
Diện tích hình chữ nhật là:
136 . 34 = 4624 (m²)
Đáp số: 4624 m2.
Câu 69:
Cho \(\overline {abcd} + \overline {badc} \)= 3487. Tìm a + b + c + d.
 Xem đáp án
Xem đáp án
Ta có:
\(\overline {abcd} + \overline {badc} \)= 3487
⇔ 1000a + 100b + 10c + d + 1000b + 100a + 10d + c = 3487
⇔ 1100 a + 1100b + 11c + 11d = 3487
⇔ 11 (100a + 100b + c + d) = 3487
⇔100a + 100b + c + d = 317
Do c + d có chữ số tận cùng là 7
Nên \(\left[ \begin{array}{l}c + d = 7\\c + d = 17\end{array} \right.\)
Với c + d = 7, thì a + b = 3,1 (loại)
Với c + d = 17, thì a + b = 3
Vậy a + b + c + d = 17 + 3 = 20.
Câu 70:
Bạn An và Khang đi mua 18 gói bánh và 12 gói kẹo để lớp liên hoan An đưa cho cô bán hàng bốn tờ 50 nghìn đồng và được cô trả lại 72 nghìn đồng. Khang nói: “cô tính sai rồi”. Bạn hãy cho biết Khang nói đúng hay sai ? Giải thích tại sao ?
 Xem đáp án
Xem đáp án
Do bạn An và bạn Khang đi mua tất cả là 30 gói bánh kẹo nên số tiền phải trả bắt buộc phải chia hết cho 3
Số tiền bạn An đưa cho cô bán hàng là: 4 . 50000 = 200000 (đồng)
Số tiền cô bán hàng nhận là: 200000 – 72000 = 128000(đồng)
Vì 128000 chia hết cho 3 nên bạn Khang nói đúng.
Câu 71:
Tính bằng cách thuận tiện nhất: \(\frac{7}{{19}}.\frac{1}{3} + \frac{7}{{19}}.\frac{2}{3}\).
 Xem đáp án
Xem đáp án
\(\frac{7}{{19}}.\frac{1}{3} + \frac{7}{{19}}.\frac{2}{3}\)= \(\frac{7}{{19}}.\left( {\frac{1}{3} + \frac{2}{3}} \right)\)= \(\frac{7}{{19}}.1\)= \(\frac{7}{{19}}\).
Câu 72:
Các số chia hết cho 11 khi nào?
 Xem đáp án
Xem đáp án
Các số chia hết cho 11 khi tổng các chữ số hàng lẻ trừ tổng các chữ số hàng chẵn hoặc ngược lại chia hết cho 11.
Ví dụ: số 253 có (2 + 3) – 5 = 0 ⋮ 11 nên 253 ⋮ 11.
Câu 74:
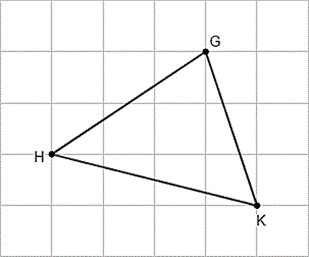
Tính diện tích tam giác GHK biết diện tích một ô vuông nhỏ là 10 cm2.
 Xem đáp án
Xem đáp án
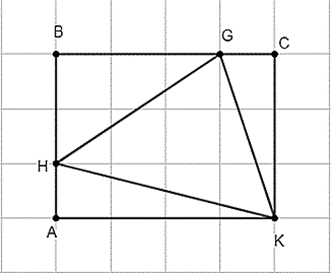
Vì diện tích một ô vuông nhỏ là 10 cm2 nên cạnh hình vuông là \(\sqrt {10} \)cm
SGKC = \[\frac{1}{2}.GC.CK = \frac{1}{2}.\sqrt {10} .3\sqrt {10} = 15\](cm2)
SBHG = \[\frac{1}{2}.BH.BG = \frac{1}{2}.2\sqrt {10} .3\sqrt {10} = 30\](cm2)
SAHK =\[\frac{1}{2}.AH.AK = \frac{1}{2}.\sqrt {10} .4\sqrt {10} = 20\](cm2)
SABCK =\[4\sqrt {10} .3\sqrt {10} = 120\](cm2)
SGHK = SABCK – (SGKC + SBHG + SAHK) = 120 – (15 + 30 + 20) = 55 (cm2).
Câu 75:
Cho tam giác ABC có \(\widehat A\)= 120°, AB = 3 cm, AC = 6 cm. Tính độ dài đường phân giác AD.
 Xem đáp án
Xem đáp án
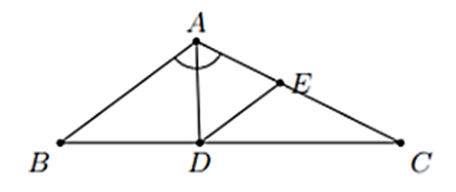
Qua D kẻ DE // AB
Ta có: \(\widehat {ADE}\, = \,\widehat {BAD}\,\)(hai góc so le trong, DE // AB)
⇒ \(\widehat {ADE}\, = \,\widehat {DAE}\,\)( cùng bằng 60°) suy ra tam giác ADE là tam giác đều.
Đặt AD = DE = EA = x. Ta có:
\(\frac{{DE}}{{AB}}\, = \,\frac{{CE}}{{CA}}\,\,\,\,hay\,\,\,\frac{x}{3}\, = \,\frac{{6 - x}}{6}\)
Từ đó x = 2.
Vậy AD = 2 cm.
Câu 76:
Phân số \(\frac{{24056}}{{1000}}\) được viết thành số thập phân là?
 Xem đáp án
Xem đáp án
\(\frac{{24056}}{{1000}}\)= 24,056.
Câu 77:
Một người nuôi 85 con gà. Sau khi người đó mua thêm 20 con gà trống bằng \(\frac{3}{4}\)số gà mái. Hỏi lúc đầu người đó mua bao nhiêu con gà trống, bao nhiêu con gà mái?
 Xem đáp án
Xem đáp án
Sau khi người đó mua thêm 20 con gà trống thì tổng số gà là:
85 + 20 = 105 (con)
Coi số gà trống là 3 phần bằng nhau thì số gà mái là 4 phần bằng nhau như thế
Số gà mái lúc đầu là:
105 : (3 + 4) . 4 = 60 (con)
Số gà trống lúc đầu là :
85 – 60 = 25 (con).
Câu 78:
Cho phép tính : 30 + 31 + 32 + 33 + ..........+ 32008 + 32009. Lấy kết quả phép tính này chia cho 8 thì số dư là bao nhiêu ?
 Xem đáp án
Xem đáp án
Số số của dãy trên là:
(32009 – 30) : 1 + 1 = 31980 (số)
Số cặp số của dãy là:
31980 : 2 = 15990 (cặp)
Ta có:
30 + 31 + 32 +....+ 32008 + 32009
= (30 + 32009) + (31 + 32008) + ...
= 32039 . 15990
= 512303610
Vậy 512303610 : 8 = 64037951(dư 2).
Câu 79:
Rút gọn biểu thức: \[\frac{{48{x^7}{y^2}z}}{{6{x^2}{y^3}}}\].
 Xem đáp án
Xem đáp án
\[\frac{{48{x^7}{y^2}z}}{{6{x^2}{y^3}}} = 8{x^{7 - 2}}{y^{2 - 3}}z = 8{x^5}{y^{ - 1}}z = \frac{{8{x^5}z}}{y}\].
Câu 80:
Một ô tô trong 5 giờ đầu, mỗi giờ đi được 247 km. Trong 3 giờ sau mỗi giờ đi được 43km. Trung bình mỗi giờ đi được bao nhiêu km?
 Xem đáp án
Xem đáp án
Tổng số km ô tô đi được trong 8 giờ là:
5 . 247 + 3 . 43 = 1364
Trung bình mỗi giờ ô tô đi được số km là:
1364 : 8 = 170,5 (km).
Câu 82:
Tìm giá trị nhỏ nhất của biểu thức: B = x2 + y2 – x + 6y + 10.
 Xem đáp án
Xem đáp án
Ta có:
B = x2 + y2 – x + 6y + 10 = \[\left( {{x^2} - x + \frac{1}{4}} \right) + \left( {{y^2} + 6y + 9} \right) + \frac{3}{4} = {\left( {x - \frac{1}{2}} \right)^2} + {\left( {y + 3} \right)^2} + \frac{3}{4}\]
Vì \[{\left( {x - \frac{1}{2}} \right)^2} + {\left( {y + 3} \right)^2}\]≥ 0 với mọi x, y
Suy ra: B ≥ \[\frac{3}{4}\]
Vậy giá trị nhỏ nhất của B là \[\frac{3}{4}\] khi \(\left\{ \begin{array}{l}x = \frac{1}{2}\\y = - 3\end{array} \right.\).
Câu 83:
Cho nửa đường tròn tâm O, đường kính AB.Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên đường tròn (M khác A; B), vẽ tiếp tuyến với nửa đường tròn ,cắt Ax và By lần lượt tại C và D.
a) Chứng minh rằng: \(\widehat {COD}\)= 90°.
b) Chứng minh AC . BD không đổi.
 Xem đáp án
Xem đáp án
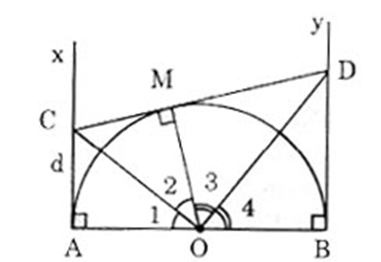
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OC là tia phân giác của \(\widehat {AOM}\)
OD và tia phân giác của \(\widehat {BOM}\)
OC và OD là các tia phân giác của hai góc kề bù \(\widehat {AOM}\)và \(\widehat {BOM}\) nên OC ⊥ OD
Suy ra: \(\widehat {COD}\)= 90°
b) Ta có: AC = CM, BD = DM (theo tính chất 2 tiếp tuyến cắt nhau)
Nên AC.BD = CM.MD (1)
ΔCOD vuông tại O, ta có:
CM.MD = OM2 = R2 (R là bán kính đường tròn O). (2)
Từ (1) và (2) ta có: AC.BD = CM.MD = R2
Vậy AC.BD = R2 (không đổi).
Câu 84:
Cho trước hai điểm A, B phân biệt. Tìm tập hợp các điểm M thoả mãn \(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right|\).
 Xem đáp án
Xem đáp án
\(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right|\)⇔ MA = MB
Suy ra: tập hợp M là đường trung trực của đoạn thẳng AB.
Câu 85:
Có 36 con vừa gà vừa chó. Tổng số chân của 36 con vừa gà vừa chó bằng 100. Hỏi có bao nhiêu con gà, bao nhiêu con chó?
 Xem đáp án
Xem đáp án
Gọi x là số con gà, y là số con chó chó (x, y > 0)
1 con gà có 2 chân, 1 con chó có 4 chân.
Theo bài ra ta có:
x + y = 36
2x + 4y = 100
Giải hệ phương trình : x = 22; y = 14
Vậy có 22 con gà và 14 con chó.
Câu 86:
Nếu chỉ vòi thứ nhất chảy thì sau 8 giờ nước sẽ đầy bể; nếu chỉ vòi thứ hai chảy thì sau 24 giờ nước sẽ đầy bể. Lúc đầu người ta cho cả hai vòi cùng chảy vào bể trong 1 giờ, sau đó để một mình vòi thứ hai chảy. Hỏi sau bao lâu nữa thì vòi thứ hai sẽ chảy đầy bể?
 Xem đáp án
Xem đáp án
Mỗi giờ vòi thứ nhất chảy được \(\frac{1}{8}\) bể.
Mỗi giờ vòi thư hai chảy được \(\frac{1}{{10}}\) bể.
Mỗi giờ cả hai vòi chảy được: \(\frac{1}{8}\) + \(\frac{1}{{10}}\)= \(\frac{9}{{40}}\) (bể)
Thời gian cần để nước chảy đầy bể: 1: \(\frac{9}{{40}}\) = \(\frac{{40}}{9}\) (giờ).
Câu 87:
Hiện nay tuổi bố gấp 4 lần tuổi con biết rằng 5 năm nữa thì tổng số tuổi của hai bố con là 55 tuổi. Hỏi hiện nay bố bao nhiêu tuổi ? Con bao nhiêu tuổi?
 Xem đáp án
Xem đáp án
Tổng số tuổi của bố và con hiện nay là:
55 – (5 + 5) = 45 (tuổi)
Tổng số phần bằng nhau là:
1 + 4 = 5 (phần)
Tuổi bố hiện tại là :
45 : 5 . 4 = 36 (tuổi)
Tuổi con hiện tại là :
45 – 36 = 9 (tuổi)
Câu 88:
Khi nhân một số thập phân với 16,3 do sơ xuất một bạn học sinh đã đặt các tích riêng thẳng cột như trong phép cộng nên được 12,6. Tìm kết quả đúng với phép nhân đó.
 Xem đáp án
Xem đáp án
Theo bài ra, 12,6 gấp thừa số thứ nhất số lần là:
(1 + 6 + 3) : 10 = 1 (lần)
Thừa số thứ nhất là:
12,6 : 1 = 12,6
Tích đúng là:
12,6 . 16,3 = 205,38.
Câu 89:
 Xem đáp án
Xem đáp án
1 + 3 + 5 + ... + 19 – 2 – 4 – … – 18
= (1 + 3 + 5 + ... + 19) – (2 + 4 +… + 18)
= \(\left( {\frac{{19 - 1}}{2} + 1} \right)\frac{{\left( {19 + 1} \right)}}{2}\)– \(\left( {\frac{{18 - 2}}{2} + 1} \right)\frac{{\left( {18 + 2} \right)}}{2}\)
= 100 – 90
= 10.
Câu 90:
Hình bình hành ABCD có độ dài đáy DC là \(\frac{1}{4}\) m, chiều cao AH là 2 dm 4 cm. Tính diện tích hình đó dưới dạng dm.
 Xem đáp án
Xem đáp án
Đổi 2 dm 4 cm = 24 cm
\(\frac{1}{4}\) m = 25 cm.
Diện tích hình bình hành là :
24 . 25 = 600 (cm2).
Đổi 600 cm2 = 6 dm2.
Câu 91:
Một hợp tác xã dự định trồng rau sạch trên diện tích là 1ha 422m2. Người ta đã trồng được \(\frac{4}{9}\) diện tích đó. Hỏi hợp tác xã còn lại bao nhiêu mét vuông chưa trồng rau?
 Xem đáp án
Xem đáp án
Đổi 1ha 422 m2 = 10422 m2
Người ta đã trồng được số diện tích là:
10422 . \(\frac{4}{9}\) = 4632 (m2)
Hợp tác xã đó còn lại số mét vuông chưa trồng rau là:
10 422 – 4632 = 5790 (m2)
Đáp số: 5790 m2.
Câu 92:
Một miếng đất hình chữ nhật có chiều dài là 64 m chiều rộng là 34 m.
a) Tính chu vi mảnh đất đó
b) Người ta giảm 8m chiều dài và tăng chiều rộng để miếng đất thành hình vuông, biết phần diện tích giảm theo chiều dài là 272 m2. Tính phần diện tích tăng thêm theo chiều rộng?
 Xem đáp án
Xem đáp án
a) Diện tích mảnh đất lúc đầu là:
64 . 34 = 2176 (m2).
b) Diện tích mảnh đất khi bị giảm chiều dài và giữ nguyên chiều rộng là:
2176 – 272 = 1904 (m2).
Chiều dài khi bị giảm là:
1904 : 34 = 56 (m).
Nếu chiều rộng tăng lên và bớt chiều dài thì diện tích hình vuông là:
56 . 56 = 3136 (m2).
Phần diện tích tăng thêm theo chiều rộng là:
3136 – 2176 = 960 (m2).
Đáp số: 960 m2.
Câu 93:
Một tấm bìa hình vuông có cạnh \(\frac{3}{8}\)m. Tính chu vi và diện tích tấm bìa đó.
 Xem đáp án
Xem đáp án
Đổi \(\frac{3}{8}\)m = 0,375 m
Chu vi tấm bìa là:
4 . 0,375 = 1,5 (m).
Diện tích tấm bìa là:
0,375 . 0,375 = 0,140625 (m2).
Câu 94:
Mội tổ có 8 công nhân làm trong 4 giờ được 120 sản phẩm. Hỏi 8 công nhân đó làm trong 3 giờ được bao nhiêu sản phẩm ? (Biết mức làm của mỗi người người như nhau).
 Xem đáp án
Xem đáp án
Số sản phẩm mỗi giờ làm được là:
120 : 4 = 30 (sản phẩm)
Trong 3 giờ làm được số sản phẩm là:
30 . 3 = 90 (sản phẩm).
Đáp số: 90 sản phẩm.
