- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 57)
-
12947 lượt thi
-
69 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Có bao nhiêu số tự nhiên có 4 chữ số và chia hết cho ít nhất một trong ba số 3, 4, 5.
 Xem đáp án
Xem đáp án
Gọi A1 là tập các số có 4 chữ số chia hết cho 3
A2 là tập các số có 4 chữ số chia hết cho 4
A3 là tập các số có 4 chữ số chia hết cho 5
Theo nguyên lý bao hàm loại trừ:
\[|{A_1} \cup {A_2} \cup {A_3}| = |{A_1}| + |{A_2}| + |{A_3}| - |{A_1} \cap {A_2}| - |{A_2} \cap {A_3}| - |{A_1} \cap {A_3}| + |{A_1} \cap {A_2} \cap {A_3}|\]
= 3000 + 2250 + 1800 − 750 − 450 − 600 + 150
= 5400 (số).
Câu 2:
Lớp 4A có ba tổ tham gia trồng cây, tổ 1 có 12 bạn mỗi bạn trồng được 8 cây. Tổ 2 trồng được 72 cây, tổ 3 trồng được 84 cây. Hỏi trung bình mỗi tổ trồng được bao nhiêu cây?
 Xem đáp án
Xem đáp án
Tổ 1 trồng được số cây là:
12 × 8 = 96 (cây)
Trung bình 1 đội có số cây là:
(96 + 72 + 84) : 3 = 84 (cây)
Đáp số: 84 cây.
Câu 3:
Lớp 12B có ba tổ tham gia trồng cây, tổ 1 có 7 bạn mỗi bạn trồng được 12 cây. Tổ 2 có 8 người trồng được 90 cây, tổ 3 có 10 người trồng được 76 cây. Hỏi trung bình mỗi người trồng được bao nhiêu cây?
 Xem đáp án
Xem đáp án
Tổng ba tổ có tất cả số người là:
7 + 8 + 10 = 25 (người)
Tổ 1 trồng được số cây là:
12 × 7 = 84 (cây)
Tổng số cây 3 tổ trồng được là:
84 + 90 + 76 = 250 (cây)
Trung bình mỗi người trồng được số cây là:
250 : 25 = 10 (cây)
Đáp số: 10 cây.
Câu 4:
Một thư viện trường học cho học sinh mượn 65 quyển sách gồm hai loại: sách giáo khoa và sách đọc thêm. Số sách giáo khoa nhiều hơn sách đọc thêm là 17 quyển. Hỏi thư viện đã cho học sinh mượn mỗi loại bao nhiêu quyển sách?
 Xem đáp án
Xem đáp án
Số sách đọc thêm thư viện cho mượn là:
(65 − 17) : 2 = 24 (quyển)
Số sách giáo khoa thư viện cho mượn là:
65 − 24 = 41(quyển)
Đáp số: 24 quyển sách đọc thêm, 41 quyển sách giáo khoa.
Câu 5:
Nếu trong một tháng nào đó mà có 3 ngày thứ bảy đều là các ngày chẵn thì ngày 25 của tháng đó sẽ là ngày thứ mấy?
 Xem đáp án
Xem đáp án
Trong một tháng nào đó có ba ngày thứ bảy là ngày chẵn thì chắc chắn còn có hai ngày thứ Bảy là ngày lẻ. Năm ngày thứ Bảy đó sắp xếp như sau:

Số ngày nhiều nhất trong một tháng là 31 ngày. Tháng này có 4 tuần và 3 ngày. Nếu thứ bảy đầu tiên là ngày mùng 4 thì tháng đó sẽ có số ngày là:
4 + 7 × 4 = 32 (ngày)
Vì 1 tháng nhiều nhất có 31 ngày nên 32 ngày là trái với lịch thông thường.
Vì vậy thứ bảy đầu tiên (1) phải là ngày mùng 2, thứ 7 thứ tư (4) sẽ là ngày:
2 + 7 × 3 = 23
Vậy ngày 25 của tháng đó là ngày thứ hai.
Cách 2.
Lập bảng theo tuần lễ:
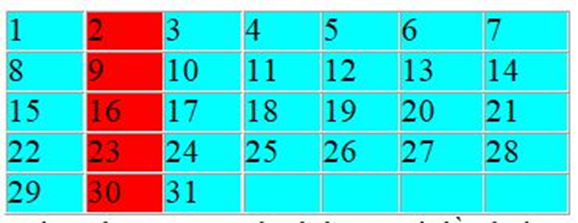
Trong 3 cột đầu tiên chỉ có cột 2 thích hợp với đầu bài toán. Cột này có 5 ngày thứ bảy. Vì ngày 23 là thứ bảy, nên ngày 25 là thứ hai.
Câu 6:
Tìm trung bình cộng của dãy số sau: 3; 6; 9; 12; …1998; 2001.
 Xem đáp án
Xem đáp án
Ta thấy: Các số trên lập thành một dãy số cách đếu với khoảng cách giữa 2 số liền nhau là 3 đơn vị.
Có số số hạng là: (2001 − 3) : 3 + 1 = 667 (số)
Tổng dãy số trên là: (2001 + 3) × 667 : 2 = 668334
Trung bình cộng của dãy số trên là: 668334 : 667 = 1102
Đáp số: trung bình cộng của dãy số là 1102.
Câu 7:
Tích 1 × 2 × 3 × ... × 50 có tận cùng bao nhiêu chữ số 0?
 Xem đáp án
Xem đáp án
Trong tích đã cho ta có các thừa số tận cùng bằng 0 là: 10, 20, 30, 40, 50 và tận cùng bằng 5 là: 5, 15, 25, 35, 45.
- Tích 10 × 20 × 30 × 40 tận cùng bằng 4 chữ số 0.
Tích của 50 và một số chẵn (50 × 2 chẳng hạn) tận cùng bằng 2 chữ số 0.
- Tích 25 × 24 tận cùng bằng 2 chữ số 0.
- Mỗi số 5, 15, 35, 45 nhân với một số chẵn (ngoài những số đã lấy ở trên) cho một số tận cùng bằng một chữ số 0.
Thí dụ: 5 × 6; 15 × 8; 35 × 34; 45 × 44; đều tận cùng bằng 1 chữ số 0.
Ngoài ra, không còn có hai thừa số nào có tích tận cùng bằng 0.
Ta có:
4 + 2 + 2 + 4 = 12 chữ số 0
Đáp số: 12 chữ số 0.
Câu 8:
Tích 5 × 10 × 15 × 20 × 25 × 30 × ... × 100 có tận cùng bao nhiêu chữ số 0?
 Xem đáp án
Xem đáp án
Ta thấy tích đó có:
+ Các số 10, 20, 30, 40, ..., 90 có 1 chữ số 0 và 100 có 2 chữ số không. Tổng cộng là 11 chữ số 0.
Vậy Tích (1): 10 × 20 × 30 × 40 ×... × 100 sẽ tận cùng 11 chữ số 0.
+ Các số 5, 15, 25, 35, ..., 95 không có chữ số 0, mà các số tận cùng bằng 5 nhân với nhau sẽ không bao giờ tận cùng bằng 0.
Vậy Tích (2): 5 × 15 × 25 × 35 × ... × 95 sẽ không tận cùng chữ số 0 nào
Vậy Tích (1) × Tích (2) = 5 × 10 × 15 × 20 × 25 × 30 × ... × 100 sẽ tận cùng bằng 11 chữ số 0.
Câu 9:
Tính tổng các số tự nhiên nhỏ hơn 6.
 Xem đáp án
Xem đáp án
Tổng các số tự nhiên nhỏ hơn 6 là: 1 + 2 + 3 + 4 + 5 = 15
Đáp số: tổng các số tự nhiên nhỏ hơn 6 là 15.
Câu 10:
Cho ∆ABC có E là trung điểm của AC. Qua E kẻ ED // AB (D ∈ BC), EF // BC (F ∈ AB).
a) Chứng minh tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.
b) Gọi H là điểm đối xứng của D qua F. CHứng minh rằng HB // AD.
c) Gọi I là trung điểm của HB, K là giao điểm của AD và EF. Chứng minh rằng I, K, E thẳng hàng.
d) ∆ABC cần thêm điều kiện gì để HF = \[\frac{{AB}}{2}\].
 Xem đáp án
Xem đáp án
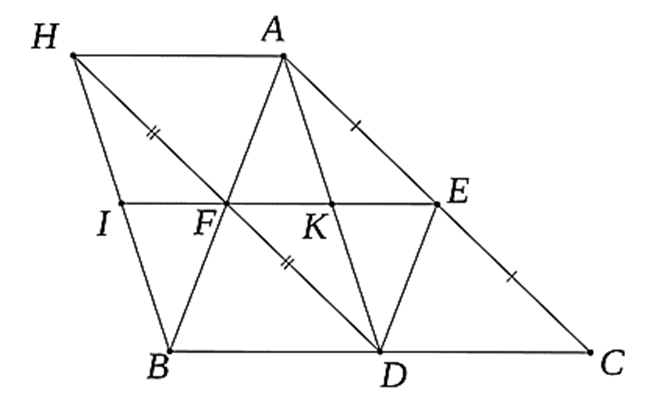
a)
Xét tứ giác BDEF có:
EF // BD (vì EF // BC)
ED // FB (vì ED // AB)
Do đó tứ giác BDEF là hình bình hành (tứ giác có cặp cạnh đối song song)
Tam giác ABC có:
EA = EC (gt)
ED // AB (gt)
Do đó DB = DC hay D là trung điểm của đoạn thẳng BC.
b)
Vì H đối xứng D qua F
⇒ F là trung điểm của HD (1)
Vì E là trung điểm của AC và EF // BC
⇒ F là trung điểm của AB (2)
Từ (1) và (2) ta có tứ giác HABD có hai đường chéo cắt nhau tại trung điểm mỗi đường.
⇒ AHBD là hình hình hành
⇒ HB // AD.
c)
Xét tam giác ∆HBD có:
I là trung điểm của HB
F trung điểm của HD
⇒ IF // BD (3)
Mà FE // BD (4)
⇒ I, F, E thẳng hàng.
⇒ I, K, E thẳng hàng.
d) Để HF = \(\frac{{AB}}{2}\) thì \(\frac{{HD}}{2} = \frac{{AB}}{2}\)
⇒ HD = AB
Hình bình hành AHBD có HD = AB
⇒ AHBD là hình chữ nhật
⇒ AD vuông góc với BC
Xét tam giác ABC có AD vừa là đường cao vừa là đường trung tuyến (D là trung điểm của BC)
⇒ ΔABC cân tại A.
Vậy ∆ABC cân tại A thì HF = \(\frac{{AB}}{2}\).
Câu 11:
Tính nhanh: 1.4 + 2.5 + 3.6 + ... + 100.103.
 Xem đáp án
Xem đáp án
Đặt A = 1.4 + 2.5 + 3.6 + ... + 100.103
= 1(2.2) + 2(3 + 2) + 3(4+ 2) + ...+ 100(101+ 2)
= 1.2 + 2.3 + 3.4 + ...+ 100.101 + (1.2 + 2.2 + 3.2 + ... + 100.2)
= 1.2 + 2.3 + 3.4 + ... + 100.101 + 2(1 + 2 + 3 + ... + 100)
= 1.2 + 2.3 + 3.4 + ... + 100.101 + 10100
Đặt B = 1.2 + 2.3 + 3.4 + ... + 100.101
⇒ 3B = 1.2.3 + 2.3.3 + 3.4.3 + 100.101.3
⇒ 3B = 1.2.3 + 2.3(4 – 1) + 3.4(5 – 2) + ... + 100.101(102 − 99)
⇒ 3B = 1.2.3 + 2.3.4 − 1.2.3 + 3.4.5 − 2.3.4 + ... + 100.101.102 − 99.100.101
⇒ 3B = 100.101.102
⇒ B = 343400
Khi đó A = B + 10100 = 343400 + 10100 = 353500
Câu 12:
12m2 + 9dm2 = … dm2
 Xem đáp án
Xem đáp án
Ta có: 1m2 = 100dm2
Vậy 12m2 + 9dm2 = 1200dm2 + 9dm2 = 1209dm2.
Đáp số: 1209 dm2
Câu 13:
16h40p là bao nhiêu giờ?
 Xem đáp án
Xem đáp án
Ta có: 16 giờ = 16 × 60 phút = 960 phút
16 giờ 40 phút = 1000 phút = \(\frac{{1000}}{{60}} = \frac{{50}}{3}\)giờ
Đáp số: 16 giờ 40 phút = \(\frac{{50}}{3}\) giờ.
Câu 14:
Hai người thợ nếu làm chung 1 công việc thì sau 5 giờ sẽ xong. Nhưng sau khi cùng làm được 3 giờ thì người thợ cả có việc bận nghỉ làm. Người thợ thứ 2 làm nốt chỗ công việc còn lại mất 6 giờ mới xong. Hỏi nếu mỗi người làm một mình chỗ công việc đó thì phải mất bao nhiêu thời gian?
 Xem đáp án
Xem đáp án
Trong 1 giờ, cả hai người làm được là:
1 : 5 = \(\frac{1}{5}\) (giờ)
Trong 3 giờ, cả hai làm được là:
\(\frac{1}{5}\) × 3 = \(\frac{3}{5}\) (công việc)
Số công việc người thứ hai làm xong trong 6 giờ là:
1 − \(\frac{3}{5}\) = \(\frac{2}{5}\) (công việc)
Nếu 1 mình người thứ hai làm thì xong trong:
\(6:\frac{2}{5} = 15\) (giờ)
Một mình người thợ cả làm xong trong:
1 : (\(\frac{1}{5}\) – 1 : 15) = 7,5 (giờ)
Đổi: 7,5 giờ = 7 giờ 30 phút
Đáp số: Người thợ cả làm xong công việc một mình hết 7 giờ 30 phút.
Người thợ thứ hai làm xong công việc một mình hết 15 giờ.
Câu 15:
Hai người thợ nếu làm chung 1 công việc thì sau 5 giờ sẽ xong. Nhưng sau khi cùng làm được 2 giờ thì người thứ hai có việc bận phải nghỉ làm. Người thứ nhất phải làm thêm 9 giờ mới xong. Hỏi nếu làm riêng thì mỗi người sẽ mất bao nhiêu thời gian?
 Xem đáp án
Xem đáp án
Trong một giờ, cả hai người làm được là:
1 : 5 = \(\frac{1}{5}\) (giờ)
Trong hai giờ, cả hai làm được là:
\(\frac{1}{5}\) × 2 = \(\frac{2}{5}\) (công việc)
Để làm \(\frac{3}{5}\) số công việc còn lại, người thứ nhất mất 9 giờ. Vậy để hoàn thành toàn bộ công việc, người đó mất số thời gian là:
9 : \(\frac{3}{5}\) = 15 (giờ)
Một giờ người thứ nhất làm được số công việc là:
1 : 15 = \(\frac{1}{{15}}\)(công việc)
Một giờ người thứ hai làm được số công việc là:
\(\frac{1}{5} - \frac{1}{{15}} = \frac{2}{{15}}\) (giờ)
Thời gian để người thứ hai làm xong công việc là:
\(1:\frac{2}{{15}} = \frac{{15}}{2}\)giờ = 7,5 giờ = 7 giờ 30 phút\(\)
Đáp số: Người thợ thứ hai làm xong công việc một mình hết 7 giờ 30 phút.
Người thợ thứ nhất làm xong công việc một mình hết 15 giờ.
Câu 16:
Tìm x: \({3^{x - 1}} = \frac{1}{{243}}\).
 Xem đáp án
Xem đáp án
\[\begin{array}{l}{3^{x - 1}} = \frac{1}{{243}}\\ \Rightarrow {3^{x - 1}} = {3^{ - 5}}\\ \Rightarrow x - 1 = - 5\\ \Rightarrow x = - 5 + 1\\ \Rightarrow x = - 4\end{array}\]
Đáp số: x = \[ - 4\].
Câu 17:
Tính tổng:\[\frac{6}{8} + \frac{6}{{56}} + \frac{6}{{140}} + ... + \frac{6}{{1100}} + \frac{6}{{1400}}\].
 Xem đáp án
Xem đáp án
\[\begin{array}{l}\frac{6}{8} + \frac{6}{{56}} + \frac{6}{{140}} + ... + \frac{6}{{1100}} + \frac{6}{{1400}}\\ = \frac{3}{4} + \frac{3}{{28}} + \frac{3}{{140}} + ... + \frac{3}{{550}} + \frac{3}{{700}}\\ = \frac{3}{{1.4}} + \frac{3}{{4.7}} + \frac{3}{{7.10}} + ... + \frac{3}{{22.25}} + \frac{3}{{25.28}}\\ = 1 - \frac{1}{4} + \frac{1}{4} - \frac{1}{7} + \frac{1}{7} - \frac{1}{{10}} + ... + \frac{1}{{22}} - \frac{1}{{25}} + \frac{1}{{25}} - \frac{1}{{28}}\\ = 1 - \frac{1}{{28}}\\ = \frac{{28}}{{28}} - \frac{1}{{28}}\\ = \frac{{27}}{{28}}\end{array}\]
Câu 18:
Ba bạn Hùng Thắng Minh góp tiền ủng hộ người nghèo. Hùng góp 45000 đồng, Thắng góp 30000 đồng, Minh góp số tiền kém mức trung bình cộng của 3 bạn là 3000 nghìn. Hỏi Minh góp bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Minh góp kém mức trung bình cộng của 3 bạn là 3000 đồng thì hai bạn Hùng, Thắng bù cho Minh 3000 đồng đó.
Mức trung bình cộng của cả ba bạn là:
(45000 + 30000 – 3000) : 2 = 36000 (đồng)
Minh góp số tiền là:
36000 – 3000 = 33000 (đồng)
Đáp số: 33000 đồng.
Câu 19:
Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo M, N là trung điểm của OD và OB. Gọi E là giao điểm của AM và CD. F là giao điểm của CN và AB.
a, Chứng minh: Tứ giác AMCN là hình bình hành
b, Tứ giác AECF là hình gì?
c, Chứng minh: E, F đối xứng qua O
d, Chứng minh: EC = 2DE.
 Xem đáp án
Xem đáp án
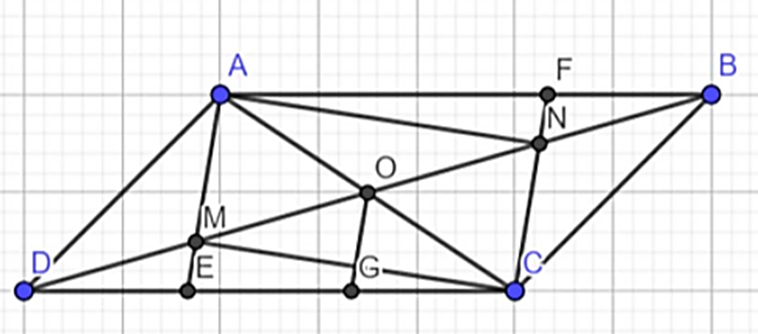
a,
Ta có ABCD là hình bình hành ⇒ AC ∩ BD tại trung điểm mỗi đường
Mà AC ∩ BD = 0 ⇒ O là trung điểm AC, DB
Lại có M, N là trung điểm OD, OB
⇒ OM = \(\frac{1}{2}\) OD = \(\frac{1}{2}\) OB = ON
⇒ O là trung điểm MN
Do O là trung điểm AC, MN
⇒ AMCN là hình bình hành (đpcm).
b,
Ta có AMCN là hình bình hành.
⇒ AM // CN
⇒ AE // CF
Mà AB // CD ⇒ AF // CE
⇒ AECF là hình bình hành.
c,
Ta có AECF là hình bình hành.
⇒ AC ∩ EF tại trung điểm mỗi đường
Mà O là trung điểm AC
⇒ O là trung điểm EF
⇒ E, F đối xứng nhau qua O (đpcm).
d,
Gọi G là trung điểm CE
Vì O là trung điểm AC ⇒ OG là đường trung bình ∆ACE
⇒ OG // AE
⇒ ME // OG
Mà M là trung điểm DO ⇒ ME là đường trung bình ∆ODG
⇒ E là trung điểm DG
⇒ DE = EG = GC
⇒ CE = CG + GE = DE + DE = 2DE (đpcm).
Câu 20:
Cho hình thang vuông ABCD vuông tại A và B. Đáy nhỏ AD = a, BC = 3a, AB = 2a. I là trung điểm của AB. Tính BA + BC, DI + DC?
 Xem đáp án
Xem đáp án
BA + BC = 2a + 3a = 5a.
Theo Pitago ta có: ID2 = AD2 + AI2 = 2a2 \[ \Rightarrow ID = a\sqrt 2 \]
Mặt khác kẻ DH vuông góc với BC thì DHBA là hình chữ nhật nên DH = 2a, BH = a. Suy ra CH = 2a.
Theo Pitago ta có:
\[\begin{array}{l}D{C^2} = D{H^2} + H{C^2} = {(2a)^2} + {(2a)^2} = 8{a^2}\\ \Rightarrow DC = 2\sqrt 2 a\end{array}\]
Vậy \[ID + DC = a\sqrt 2 + 2\sqrt 2 a = 3\sqrt 2 a\]
Câu 21:
cho tam giác abc cân tại A có BD và CE là hai đường trung tuyến của tam giác. Chứng minh tứ giác BCDE là hình thang cân.
 Xem đáp án
Xem đáp án
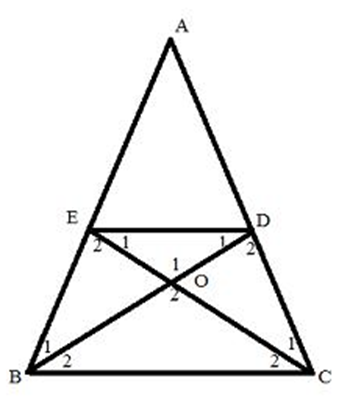
Xét ΔABC có:
\(\)\[\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\]
Do đó: DE // CB
Xét tứ giác BEDC có DE // BC nên BEDC là hình thang
Mà \[\widehat {EBC} = \widehat {DCB}\] (vì ∆ABC cân tại A)
Nên BEDC là hình thang cân
Vậy BEDC là hình thang cân.
Câu 22:
Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB theo thứ tự lấy hai điểm D và E sao cho BD = CE.
Chứng minh ∆ADE cân.
 Xem đáp án
Xem đáp án
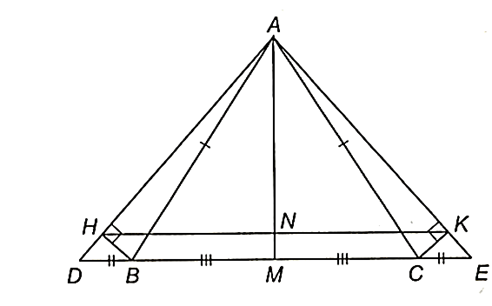
Do ∆ABC cân tại A nên \[\widehat {ABC} = \widehat {ACB}\].
Suy ra \[\widehat {ABD} = \widehat {ACE}\](cùng bù với gióc \[\widehat {ABC},\widehat {ACB}\]).
Xét ∆ABD và ∆ACE có:
AB = AC (do tam giác ABC cân tại A)
\[\widehat {ABD} = \widehat {ACE}\] (chứng minh trên),
Mà BD = CE (theo giả thiết).
Suy ra ∆ABD = ∆ACE (c.g.c),
Do đó AD = AE (hai cạnh tương ứng),
Suy ra tam giác ADE cân tại A.
Câu 23:
Cho tam giác ABC cân tại A, đường trung tuyến CM và BN. Trên tia đối của tia BA lấy điểm D sao cho BD = AB. Chứng minh CD = 2CM.
 Xem đáp án
Xem đáp án
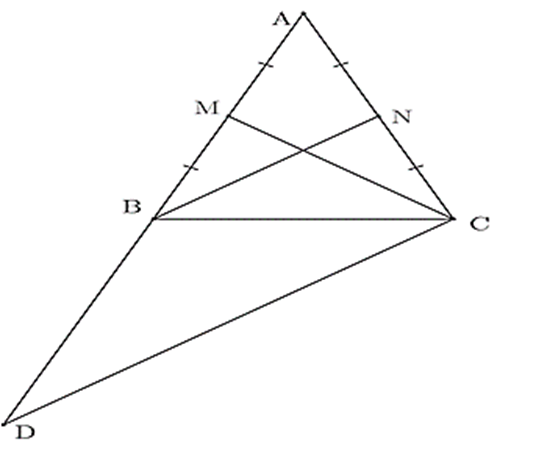
Gọi N là trung điểm cạnh AC. Suy ra BN là đường trung tuyến của ΔABC.
Vì ΔABC là tam giác cân tại A
Nên BN = CM. (1)
Xét tam giác ΔACD có B, N lần lượt là trung điểm cạnh AD và AC.
⇒ BN là đường trung bình của tam giác của ΔACD.
⇒ BN = \(\frac{1}{2}\)DC ⇒ DC = 2BN. (2)
Từ (1) và (2) suy ra CD = 2CM.
Câu 24:
Cho tam giác ABC có ba góc nhọn đường cao AH
a. CMR: AB2 + AC2 = \(\frac{{BC}}{2}\) + 2AM2
b. AC2 − AB2 = 2BC.HM (AC > AB)
 Xem đáp án
Xem đáp án
a) Ta có: AB2 + AC2 = 2AH2 + BH2 + CH2
= 2AM2 − 2HM2 + (BM − HM)2 + (CM + HM)2
= 2AM2 − 2HM2 + BM2 − 2BM.HM + HM2 + CM2 + 2CM.HM + HM2
= 2AM2 + BC2 − 2BM.CM = 2AM2 + BC2 − \(\frac{{2B{C^2}}}{4}\)
= 2AM2 + \(\frac{{B{C^2}}}{2}\)(đpcm)
b) Ta có: AC2 – AB2 = AH2 + HC2 – BH2 – AH2
= HC2 – BH2 = (CM + HM)2 − (BM − HM)2
= CM2 + 2CM.HM + HM2 – BM2 + 2BM.HM – HM2
= 2HM(CM + BM)
= 2HM.BC (đpcm).
Câu 25:
Cho tam giác ABC có sin2 C = sin2 A + sin2 B. Tam giác ABC là tam giác gì? Vì sao?
 Xem đáp án
Xem đáp án
Gọi R là bán kính của đường tròn ngoại tiếp tam giác ∆ABC. Ta có:
sin2 C = sin2 A + sin2 B
⇒ \(\frac{{{C^2}}}{{4{R^2}}} = \frac{{{A^2}}}{{4{R^2}}} + \frac{{{B^2}}}{{4{R^2}}}\)
⇒ C2 = A2 + B2
⇒ ΔABC vuông tại C.
Câu 26:
Cho nửa đường tròn tâm O có đường kính AB, C là một điểm thuộc nửa đường tròn, H là hình chiếu của C trên AB. Qua trung điểm M của CH, kẻ đường thẳng vuông góc với OC, cắt nửa đường tròn tại D và E. Chứng minh rằng AB là tiếp tuyến của đường tròn (C, CD).
 Xem đáp án
Xem đáp án
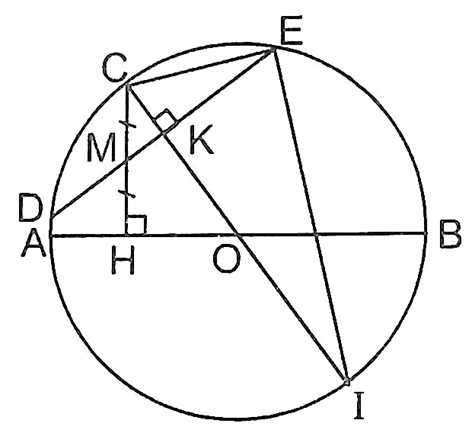
Vẽ OC cắt DE ở K và cắt đường tròn (O) ở I.
Ta có:
CE² = CK.CI = CM. (2CH) = (\(\frac{{CH}}{2}\)). (2CH) = CH²
⇒ CD = CH
⇒ CH bán kính của đường trong tâm (C). Mà CH vuông góc với AB
⇒ AB là tiếp tuyến của đường tròn (C, CD) (đpcm).
Câu 27:
Tìm một số tự nhiên biết nếu xóa chữ số 3 ở hàng đơn vị của nó đi thì nó giảm đi 1794 đơn vị.
 Xem đáp án
Xem đáp án
Ta thấy: 1794 là 9 lần số mới sau khi xóa chữ số hàng đơn vị
Mà 1794 = 199 × 9 + 3
Do đó số mới là 199
Số phải tìm là 199 thêm 3 vào hàng đơn vị: 1993.
Đáp số: 1993.
Câu 28:
Có hai sợi dây sợi thứ nhất dài hơn sợi thứ hai 54m. Nếu cắt đi 1200 cm ở mỗi sợi thì phần còn lại của sợi thứ nhất gấp 4 lần phần còn lại của sợi thứ hai. Hỏi mỗi sợi dây dài bao nhiêu mét.
 Xem đáp án
Xem đáp án
Đổi 1200cm = 12m
Nếu cắt đi 1200cm ở mỗi sợi thì phần còn lại của sợi thứ nhất hơn phần còn lại của sợi dây thứ hai 54m
Hiệu số phần bằng nhau là:
4 – 1 = 3 (phần)
Phần dây còn lại của sợi thứ 2 là:
54 : 3 × 1 = 18 (m)
Ban đầu sợi dây thứ 2 dài là:
18 + 12 = 30 (m)
Ban đầu sợi dây thứ nhất dài là:
30 + 54 = 84 (m)
Đáp số: sợi dây thứ nhất dài: 84m
sợi dây thứ hai dài: 30m.
Câu 29:
Đoạn thẳng AB dài 1km gồm hai đoạn thẳng AM và MB. Biết đoạn thẳng AM bằng \(\frac{2}{3}\) đoạn thẳng MB. Tính độ dài đoạn thẳng MB.
 Xem đáp án
Xem đáp án
Tổng số phần bằng nhau là:
2 + 3 = 5 phần
Độ dài đoạn MB là:
1 : 5 × 3 = 0,6 (km)
Đáp số: Độ dài đoạn MB là: 0,6km.
Câu 30:
Lớp 10A có 45 học sinh trong kì thi học kì 1 có 25 em đạt loại giỏi môn toán, 20 em đạt loại giỏi môn lý, 18 em đạt loại giỏi môn hoá. 6 em ko đạt loại giỏi bất kì môn nào, 5 em đạt loại giỏi 3 môn. Hỏi số học sinh chỉ đạt giỏi một môn và số học sinh giỏi hai môn?
 Xem đáp án
Xem đáp án
Tổng số bài kiểm tra đạt loại giỏi là:
25 + 20 + 18 = 63 (bài kiểm tra)
Trong đó có 5 học sinh giỏi cả 3 môn, vậy số học sinh đạt loại giỏi ít hơn 3 môn là:
45 − 5 = 40 (học sinh)
Số bài đạt điểm giỏi cho 40 học sinh đạt loại giỏi ít hơn 3 môn là:
63 – 5 × 3 = 48 (bài kiểm tra)
Mặt khác có 6 học sinh ko đạt giỏi môn nào nên 48 điểm giỏi nằm trong:
40 – 6 = 34 (học sinh)
Hay nói cách khác trong 34 học sinh sẽ có x học sinh giỏi 1 môn và y học sinh giỏi 2 môn và từ đó ta có phương trình x + y = 34 và x + 2y = 48 (x, y > 0)
Giải hệ phương trình này ta được x = 20, y = 14.
Vậy lớp có 20 học sinh giỏi một môn và 14 học sinh giỏi hai môn.
Câu 31:
Có ba tổ trồng cây. Tổ 1 trồng được nhiều hơn trung bình cộng số cây của mỗi tổ là 6 cây. Tổ 2 trồng được số cây nhiều hơn trung bình cộng số cây của tổ 2 và tổ 3 là 1 cây. Biết tổ 3 trồng 26 cây. Hỏi tổ một trồng bao nhiêu cây?
 Xem đáp án
Xem đáp án
Trung bình cộng số cây của tổ 2 và tổ 3 là:
(26 + 1) : 1 = 27 ( cây)
Số cây của tổ 2 trồng được là:
27 + 1 = 28 (cây)
Nếu tổ một mà hơn trung bình cộng của mỗi tổ là 6 cây thì số cây của tổ 1 là:
(26 + 28 + 6) : 2 + 6 = 36 (cây)
Đáp số: Tổ một trồng được 36 cây.
Câu 32:
Có ba tổ tham gia trồng cây tổ 1 trồng được 1353 cây. Tổ 2 trồng được số cây bằng \(\frac{1}{3}\) số cây của tổ 1. Tổ 3 trồng được số cây bằng số trung bình cộng của hai tổ đầu. Hỏi cả ba tổ trồng được bao nhiêu cây?
 Xem đáp án
Xem đáp án
Tổ hai trồng được số cây là :
1353 : 3 = 451 (cây)
Tổ ba trồng được số cây là :
(1353 + 451) : 2 = 902 (cây)
Cả ba tổ trồng được số cây là :
1353 + 451 + 902 = 2706 (cây)
Đáp số: Cả ba tổ trồng được 2706 cây.
Câu 33:
Một bếp ăn dự trữ gạo đủ cho 120 người ăn trong 18 ngày. Nay có 80 người được chuyển đi nơi khác. Hỏi số gạo đó đủ cho những người còn lại ăn trong bao nhiêu ngày? (Mức ăn mỗi người như nhau).
 Xem đáp án
Xem đáp án
Số suất ăn dành cho 120 người trong 18 ngày là:
120 × 18 = 2160 (suất)
Số người còn lại sau khi 80 người chuyển đi nơi khác là:
120 − 80 = 40 (người)
2160 suất ăn đủ cho 40 người ăn trong số ngày là:
2160 : 40 = 54 (ngày)
Đáp số: Số gạo đó đủ cho những người còn lại ăn trong 54 ngày.Câu 34:
Một đội công nhân có 63 người nhận sửa xong một khối lượng quần áo trong 11 ngày. Hỏi muốn làm xong khối lượng quần áo đó trong 9 ngày thì cần thêm bao nhiêu người nữa? (Mức làm của mỗi người là như nhau)
 Xem đáp án
Xem đáp án
Một người sửa hết khối lượng quần áo đó trong số ngày là:
63 × 11 = 693 (ngày)
Số người sau khi bổ sung là:
693 : 9 = 77 (người)
Muốn sửa khối lượng quần áo đó trong 9 ngày thì cần thêm số người là:
77 – 63 = 14 (người)
Đáp số: 14 người.
Câu 35:
Một mặt hàng trước đây đã giảm 20% so với giá bán cũ. Hỏi mặt hàng đó cần phải tăng bao nhiêu phần trăm giá hiện đang bán để trở về giá bán ban đầu?
 Xem đáp án
Xem đáp án
Gọi x là giá bán ban đầu (x > 0) ⇒ giá bán khi giảm đi 20% là 0,8x
Gọi y là % để giá trở lại như cũ (y > 0).
Ta có phương trình:
0,8x + y ∙ 0,8x = x
⇒ 0,8x ∙ (1 + y) = x
⇒ 0,8 ∙ (1 + y) = 1
⇒ y = 0,25
Vậy phải tăng thêm 25% để giá trở lại như cũ.
Đáp số: cửa hàng cần tăng 25% giá hiện đang bán để trở về giá ban đầu.
Câu 36:
Người ta mở rộng 1 thửa ruộng hình vuông theo cách sau: mở rộng lên phía trên 15m mở rộng phía dưới 10 mét thì được 1 hình chữ nhật có chu vi là 86 m. Tính diện tích thửa ruộng hình vuông?
 Xem đáp án
Xem đáp án
Phần chu vi tăng thêm là:
(15 + 10) × 2 = 50 (m)
Chu vi thửa ruộng ban đầu là:
86 – 50 = 36 (m)
Độ dài cạnh thửa ruộng ban đầu là:
36 : 4 = 9 (m)
Diện tích thửa ruộng hình vuông là:
9 × 9 = 81 (m2)
Vậy diện tích thửa ruộng hình vuông là 81 m2.
Câu 37:
Cho phân số \(\frac{{13}}{{25}}\). Hãy tìm một số tự nhiên sao cho nếu đem tử số cộng số đó và mẫu số trừ đi số đó ta được phân số mới có giá trị bằng \(\frac{9}{{10}}\).
 Xem đáp án
Xem đáp án
Tổng của tử số và mẫu số của phân số \(\frac{{13}}{{25}}\) là:
13 + 25 = 38
Khi cộng tử của phân số \(\frac{{13}}{{25}}\) và mẫu số của phân số \(\frac{{13}}{{25}}\) với cùng 1 số thì tổng của tử số với mẫu số của phân số mới không thay đổi và bằng 38.
Chia tử của phân số mới thành 9 phần thì mẫu của phân số mới là 10 phần.
Tổng số phần bằng nhau là:
9 + 10 = 19 (phần)
Giá trị 1 phần là:
38 : 19 = 2
Tử của phân số mới là:
2 × 9 = 18
Số tự nhiên cần tìm là:
18 – 13 = 5
Đáp số: 5.
Câu 38:
Chứng minh rằng: x5 – x + 2 không là số chính phương với mọi x thuộc Z.
 Xem đáp án
Xem đáp án
Ta có: x5 – x = x (x4 – 1)
= x (x – 1) (x + 1) (x2 + 1) ⋮ 3
Mà x (x – 1) (x + 1) (x2 + 1) ⋮ 3 nên x5 – x + 2 chia 3 dư 2
⇒ x5 – x + 2 phải là số chính phương (đpcm).
Câu 39:
Cho góc nhọn xOy, Oz là tia phân giác của góc đó. Qua điểm A thuộc tia Ox kẻ đường thẳng song song với Oy cắt Oz ở M. Qua M kẻ đường thẳng song song với Ox cắt Oy ở B. Chọn đáp án đúng.
 Xem đáp án
Xem đáp án
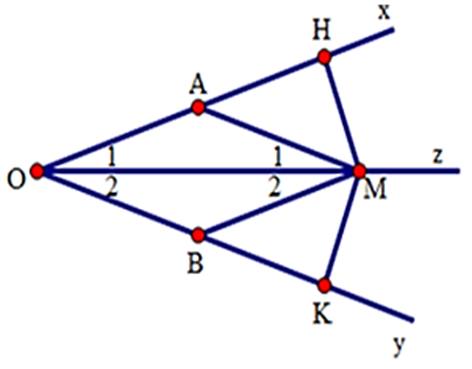
Ta có:
\[\widehat {{{\rm M}_1}} = \widehat {{O_2}}\] (Hai góc so le trong)
\[\widehat {{M_2}} = \widehat {{O_1}}\] (Hai góc so le trong)
\[\widehat {{O_1}} = \widehat {{O_2}}\] (Do Oz là tia phân giác của góc xOy)
Do đó \[\widehat {{M_2}} = \widehat {{M_1}}\]
Xét tam giác AOM và tam giác BOM có:
\[\widehat {{M_2}} = \widehat {{M_1}}\] (cmt)
OM cạnh chung
\[\widehat {{O_1}} = \widehat {{O_2}}\] (cmt)
Do đó: OA = OB, MA = MB (các cặp cạnh tương ứng)
Đáp án cần chọn là B.
Câu 40:
Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên Oz lấy điểm I. Chứng minh:
a) Tam giác ∆AOI = tam giác ∆BOI.
b) AB vuông góc với OI.
 Xem đáp án
Xem đáp án
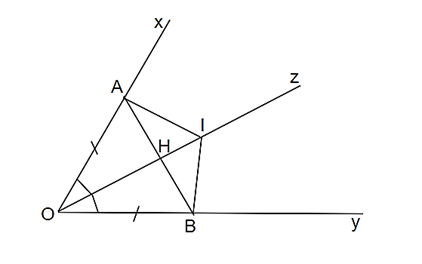
a)
Vì Oz là phân giác của xOy nên \[xOz = yOz = \frac{{xOy}}{2}\]
Xét Δ AOI và Δ BOI có:
OA = OB (gt)
AOI = BOI (cmt)
OI là cạnh chung
Do đó, Δ AOI = Δ BOI (c.g.c) (đpcm)
b)
Xét Δ AOH và Δ BOH có:
OA = OB (gt)
AOH = BOH (câu a)
HO là cạnh chung.
Do đó, Δ AOH = Δ BOH (c.g.c)
⇒ AHO = BHO (2 góc tương ứng)
Mà AHO + BHO = 180° (kề bù) nên AHO = BHO = 90°
⇒ AB ⊥ OI (đpcm).
Câu 41:
Chứng minh 79m + 1 – 79m chia hết cho 78 (m thuộc ℕ).
 Xem đáp án
Xem đáp án
79m + 1 – 79m = 79.79m – 79m
= 79m. (79 – 1)
=78.79m chia hết cho 78.
Vậy 79m + 1 – 79m chia hết cho 78 (m thuộc ℕ).
Câu 42:
Kết quả chính xác của phép tính 264 + 1 là bao nhiêu?
 Xem đáp án
Xem đáp án
264 + 1
= (1844674407 + 10000000000000000000) + 1
= 18446744000000000000 + 1
= 18446744000000000001.Câu 43:
 Xem đáp án
Xem đáp án
Gọi tích của 3 số liên tiếp là:
A= a ∙ (a + 1) ∙ (a + 2) (a thuộc ℕ*)
Giả sử a ⋮ 3 ⇒ A ⋮ 3
Nếu a ko chia hết cho 3 thì có 2 khả năng: 3n + 1 hoặc 3n + 2
Với a = 3n + 1
⇒ a + 2 = (3n + 1) + 2 = 3n + 3 ⋮ 3
⇒ A ⋮ 3 (1)
Với a = 3n + 2
⇒ a +1 = 3n + 2 + 1 = 3n + 3 ⋮ 3
⇒ A chia hết 3 (2)
Vậy với mọi A thuộc N thì A ⋮ 3 (điều đã được chứng minh).
Câu 44:
Một bếp ăn dự trữ gạo cho 80 người ăn trong 30 ngày. Nay có thêm 40 người nữa mới đến. Hỏi số gạo đó đủ ăn trong bao nhiêu ngày?
 Xem đáp án
Xem đáp án
Số suất ăn có là:
80 × 30 = 2400 (suất)
Lúc sau có số người ăn là:
80 + 40 = 120 (người)
Số gạo đó ăn trong số ngày là:
2400 : 120 = 20 (ngày)
Đáp số: Số gạo đó đủ ăn trong 20 ngày cho 120 người.
Câu 45:
Một bếp ăn dự trữ gạo cho 180 người ăn trong 10 ngày. Thực tế số người ăn giảm đi 30 người. Hỏi số gạo đó đủ ăn trong bao nhiêu ngày?
 Xem đáp án
Xem đáp án
Số người còn lại sau khi giảm đi 30 người là:
180 − 30 = 150 (người)
Số gạo đó đủ cho 150 người ăn trong số ngày là:
10 × 180 : 150 = 12 (ngày)
Đáp số: Số gạo đó đủ ăn trong 12 ngày với 150 người.
Câu 46:
 Xem đáp án
Xem đáp án
Một em bé sẽ ăn hết số gạo dự trữ trong:
20 × 120 = 2400 (ngày)
Số gạo sau khi thêm người sẽ đủ ăn trong:
20 – 4 = 16 (ngày)
Số em ở nhà trẻ sau khi thêm là:
2400 : 16 = 150 (em)
Số em mới đến thêm là:
150 – 120 = 30 (em)
Đáp số: 30 em mới đến.
Câu 47:
So sánh: 430 và 3.2410
 Xem đáp án
Xem đáp án
Ta có:
430 = 230 ∙ 230 = 230 ∙ (22)15 = 230 ∙ 415 = 230 ∙ 411 ∙ 44
3 ∙ 2410 = 3 ∙ (3.23)10 = 3 ∙ 310 ∙ 230 = 311 ∙ 230
Mà 411 ∙ 44 > 311 nên 430 > 3 ∙ 2410 .
Câu 48:
Tìm 2 phân số có tử số cùng là 1 và mẫu số là 2 số tự nhiên liên tiếp sao cho 2/\(\frac{2}{{13}}\) nằm giữa 2 phân số đó?
 Xem đáp án
Xem đáp án
Ta gọi mẫu của 2 phân số đó là b va b + 1. ( b ≠ 0, b ≠ – 1)
Khi đó ta có:
\[\frac{1}{b} > \frac{1}{{b + 1}}\]
Mà \(\frac{{13}}{{84}}\) nằm giữa 2 phân số đó
⇒ \[\frac{1}{b} > \frac{{13}}{{84}} > \frac{1}{{b + 1}}\]
⇒ \[\frac{{13}}{{13b}} > \frac{{13}}{{84}} > \frac{{13}}{{13b + 13}}\]
⇒ 13b < 84 < 13b + 13
* Do 13b < 84 ⇒ b < \(\frac{{84}}{{13}}\) (1)
* Do 84 < 13b + 13 ⇒ 71 < 13b
⇒ \(\frac{{71}}{{13}}\) < b (2)
Từ (1) và (2) \[ \Rightarrow \frac{{71}}{{13}} < b < \frac{{84}}{{13}}\] mà a là số tự nhiên
⇒ b = 6
⇒ b + 1 = 7
Vậy 2 phân số cần tìm là: \(\frac{1}{6}\)và \(\frac{1}{7}\).
Câu 49:
Số tự nhiên thích hợp để điền vào dãy số sau: 3, 17, 59, 185, 563, ... là số nào?
 Xem đáp án
Xem đáp án
Ta thấy:
Hiệu giữa 3 và 17 là 14
Hiệu giữa 17 và 59 là 42 = 14 ∙ 3
Hiệu giữa 59 và 185 là 126 = 42 ∙ 3
Hiệu giữa 185 và 563 là 378 = 126 ∙ 3
Suy ra quy luật hiệu của hai số sau sẽ gấp 3 lần hiệu của hai số trước (có lặp lại số ở giữa 2 số kia)
Vậy số cần điền là: 378 ∙ 3 + 563 = 1697.
Câu 50:
Cho \[A = \frac{1}{{1.2}} + \frac{1}{{3.4}} + \frac{1}{{5.6}} + .... + \frac{1}{{99.100}}\]. Chứng minh rằng: \(\frac{7}{{12}}\) < A < \(\frac{5}{6}\).
 Xem đáp án
Xem đáp án
Ta có \[A = \frac{1}{{1.2}} + \frac{1}{{3.4}} + \frac{1}{{5.6}} + .... + \frac{1}{{99.100}}\]
\[\begin{array}{l}A = \left( {\frac{1}{{1.2}} + \frac{1}{{3.4}}} \right) + \left( {\frac{1}{{5.6}} + ... + \frac{1}{{99.100}}} \right)\\A = \frac{7}{{12}} + \left( {\frac{1}{{5.6}} + ... + \frac{1}{{99.100}}} \right) > \frac{7}{{12}}\end{array}\]
(vì \[\frac{1}{{5.6}} + ... + \frac{1}{{99.100}} > 0\])
Ta có:
\[\begin{array}{l}A = \frac{1}{{1.2}} + \frac{1}{{3.4}} + \frac{1}{{5.6}} + ... + \frac{1}{{99.100}}\\ \Rightarrow A = \frac{1}{1} - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + ... + \frac{1}{{99}} - \frac{1}{{100}}\end{array}\]
\[ \Rightarrow A = \left( {\frac{1}{1} + \frac{1}{3} + \frac{1}{5} + ... + \frac{1}{{99}}} \right) - \left( {\frac{1}{2} + \frac{1}{4} + \frac{1}{6} + ... + \frac{1}{{100}}} \right)\]
\[ \Rightarrow A = \left( {\frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + ... + \frac{1}{{99}} + \frac{1}{{100}}} \right) - 2\left( {\frac{1}{2} + \frac{1}{4} + \frac{1}{6} + ... + \frac{1}{{100}}} \right)\]
\[\begin{array}{l} \Rightarrow A = \left( {\frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + ... + \frac{1}{{99}} + \frac{1}{{100}}} \right) - \left( {1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{50}}} \right)\\ \Rightarrow A = \frac{1}{{51}} + \frac{1}{{52}} + \frac{1}{{53}} + ... + \frac{1}{{100}}\end{array}\]
Tổng A có (100 – 51) : 1 + 1 = 50 (số hạng)
Như vậy, ta nhóm 10 số vào 1 nhóm được:
\[\begin{array}{l}A = \left( {\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}}} \right) + \left( {\frac{1}{{61}} + \frac{1}{{62}} + ... + \frac{1}{{70}}} \right)\\ + \left( {\frac{1}{{71}} + \frac{1}{{72}} + ... + \frac{1}{{80}}} \right) + \left( {\frac{1}{{81}} + \frac{1}{{82}} + ... + \frac{1}{{90}}} \right)\\ + \left( {\frac{1}{{91}} + \frac{1}{{92}} + ... + \frac{1}{{100}}} \right)\end{array}\]
Ta thấy:
\[\begin{array}{l}\left( {\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}}} \right) < 10\cdot \frac{1}{{50}} = \frac{1}{5}\\\left( {\frac{1}{{61}} + \frac{1}{{62}} + ... + \frac{1}{{70}}} \right) < 10\cdot \frac{1}{{60}} = \frac{1}{6}\\\left( {\frac{1}{{71}} + \frac{1}{{72}} + ... + \frac{1}{{80}}} \right) < 10\cdot \frac{1}{{80}} = \frac{1}{7}\\\left( {\frac{1}{{81}} + \frac{1}{{82}} + ... + \frac{1}{{90}}} \right) < 10\cdot \frac{1}{{90}} = \frac{1}{8}\end{array}\]
\[\begin{array}{l}\left( {\frac{1}{{91}} + \frac{1}{{92}} + ... + \frac{1}{{100}}} \right) < \frac{1}{9}\\ \Rightarrow \left( {\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}}} \right) + \left( {\frac{1}{{61}} + \frac{1}{{62}} + ... + \frac{1}{{70}}} \right) + \left( {\frac{1}{{71}} + \frac{1}{{72}} + ... + \frac{1}{{80}}} \right)\\ + \left( {\frac{1}{{81}} + \frac{1}{{82}} + ... + \frac{1}{{90}}} \right) + \left( {\frac{1}{{91}} + \frac{1}{{92}} + ... + \frac{1}{{100}}} \right) < \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \frac{1}{9} < \frac{5}{6}\\ \Rightarrow A < \frac{5}{6}\end{array}\]
Vậy \(\frac{7}{{12}} < A < \frac{5}{6}\).
Câu 51:
Cho \[A = \frac{1}{{1.2}} + \frac{1}{{3.4}} + \frac{1}{{5.6}} + .... + \frac{1}{{99.100}}\]
\(B = \frac{1}{{51.100}} + \frac{1}{{52.99}} + .... + \frac{1}{{99.52}} + \frac{1}{{100.51}}\)
Tính: \(\frac{A}{B}\).
 Xem đáp án
Xem đáp án
\[\begin{array}{l}A = \frac{1}{{1.2}} + \frac{1}{{3.4}} + \frac{1}{{5.6}} + .... + \frac{1}{{99.100}}\\ = \frac{{2 - 1}}{{1.2}} + \frac{{4 - 3}}{{3.4}} + \frac{{6 - 5}}{{5.6}} + .... + \frac{{100 - 99}}{{99.100}}\\ = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + .... + \frac{1}{{99}} - \frac{1}{{100}}\\ = \left( {1 + \frac{1}{3} + \frac{1}{5} + .... + \frac{1}{{99}}} \right) - \left( {\frac{1}{2} + \frac{1}{4} + \frac{1}{6} + .... + \frac{1}{{100}}} \right)\\ = \left( {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + .... + \frac{1}{{100}}} \right) - 2\left( {1 + \frac{1}{2} + \frac{1}{3} + .... + \frac{1}{{50}}} \right)\\ = \frac{1}{{51}} + \frac{1}{{52}} + .... + \frac{1}{{100}}\end{array}\]
Mặt khác:
\[\begin{array}{l}151B = \frac{{51 + 100}}{{51.100}} + \frac{{52 + 99}}{{52.99}} + .... + \frac{{99 + 52}}{{99.52}} + \frac{{100 + 51}}{{100.51}}\\ = \frac{1}{{100}} + \frac{1}{{51}} + \frac{1}{{99}} + \frac{1}{{52}} + .... + \frac{1}{{52}} + \frac{1}{{99}} + \frac{1}{{51}} + \frac{1}{{100}}\\ = \left( {\frac{1}{{100}} + \frac{1}{{99}} + .... + \frac{1}{{52}} + \frac{1}{{51}}} \right) + \left( {\frac{1}{{51}} + \frac{1}{{52}} + .... + \frac{1}{{99}} + \frac{1}{{100}}} \right)\\ = 2\left( {\frac{1}{{51}} + \frac{1}{{52}} + .... + \frac{1}{{99}} + \frac{1}{{100}}} \right)\\ = 2A\\ \Rightarrow \frac{A}{B} = \frac{{151}}{2}\end{array}\]
Vậy \[\frac{A}{B} = \frac{{151}}{2}\].
Câu 52:
Năm năm trước con 5 tuổi và kém cha 32 tuổi. Hỏi sau mấy năm nữa thì tuổi cha gấp 3 lần tuổi con?
 Xem đáp án
Xem đáp án
Hiện tại con có số tuổi là:
5 + 5 = 10 (tuổi)
Số tuổi con kém cha không bao giờ thay đổi. Ta có sơ đồ khi tuổi cha gấp 3 lần tuổi con:
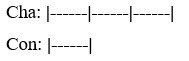
Hiệu số phần bằng nhau là:
3 − 1 = 2 (phần)
Giá trị 1 phần hay tuổi con khi đó là:
32 : 2 × 1 = 16 (tuổi)
Vậy tuổi cha gấp 3 lần tuổi con sau số năm là:
16 − 10 = 6 (năm)
Đáp số: 6 năm.
Câu 53:
Tìm số bị chia trong một phép chia cho một số có hai chữ số biết thương là 23 và số dư là 98?
 Xem đáp án
Xem đáp án
Vì số dư là 98 nên số chia là 99.
Gọi số bị chia là X.
Ta có:
X : 99 = 23 (dư 98)
X = (23 × 99) + 98
X = 2375
Vậy số bị chia là 2375.
Câu 54:
Có đường gấp khúc ABCD, có AB bằng 15cm. Biết đường gấp khúc ABC dài hơn đường gấp khúc BCD là 3cm. Tính độ dài đường gấp khúc CD.
 Xem đáp án
Xem đáp án
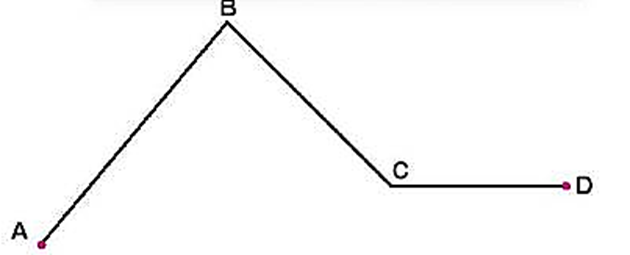
Vì ABC và BCD chung đoạn BC nên AB dài hơn CD 3cm.
Độ dài đường gấp khúc CD là :
15 − 3 = 12 (cm)
Đáp số: 12cm.
Câu 55:
Một tấm vải dài 9,7m. Người ta cắt ra 4,75m để may áo. Hỏi tấm vải còn lại dài bao nhiêu mét?
 Xem đáp án
Xem đáp án
Tấm vài còn lại dài số mét là:
9,7 – 4,75 = 4,95 (mét)
Đáp số: 4,95m.
Câu 56:
Có 8 người dự định làm xong một công việc hết 6 ngày. Nay muốn làm xong công việc đó trong vòng 3 ngày thì cần bao nhiêu người làm? (Mức làm của mỗi người như nhau)
 Xem đáp án
Xem đáp án
Muốn làm xong công việc trong một ngày cần số người là:
8 × 6 = 48 (người)
Muốn làm xong công việc trong ba ngày cần số người là:
48 : 3 = 16 (người)
Đ/S: 16 người
Câu 57:
Tìm số bị chia và số chia biết rằng thương bằng 3 số dư bằng 20 tổng của số bị chia số chia và dư bằng 136.
 Xem đáp án
Xem đáp án
Tổng của số bị chia và số chia là: 136 – 20 = 116
Gọi a là số bị chia, b là số chia.
Theo bài ra ta có:
a + b = 116 (1)
a = 3b + 20 (2)
Thay (2) vào (1) có:
3b + 20 + b = 116
4b = 116 − 20
4b = 96
⇒ b = 96 : 4 = 24 (3)
Thay (3) vào (2) có:
a = 3b + 20
= 3 × 24 + 20
= 92
Vậy số bị chia là 92, số chia là 24.
Câu 58:
Phân tích đa thức thành nhân tử: x3 + 3x2 – 4.
 Xem đáp án
Xem đáp án
x3 + 3x2 – 4 = x3 + 4x2 + 4x – x2 − 4x − 4
= x (x2 + 4x + 4) – (x2 + 4x + 4)
= (x − 1) (x2 + 4x + 4)
= (x − 1) (x + 2)2
Câu 59:
0 có chia hết cho 3 không?
 Xem đáp án
Xem đáp án
0 có chia hết cho 3 vì 0 chia cho số nào cũng bằng 0.
Nhưng 0 kông thể chia cho 0.
Câu 60:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho SN = 2ND. Tính thể tích V của khối tứ diện ACMN.
 Xem đáp án
Xem đáp án
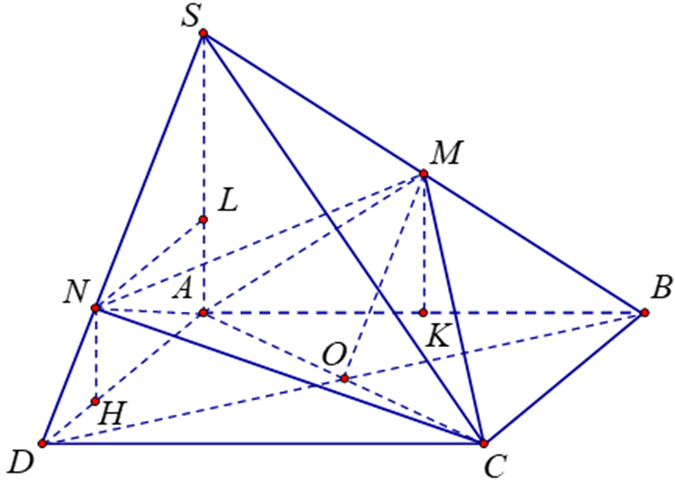
Ta có : VS.ABCD =\(\frac{1}{3}\)SABCD . SA=\(\frac{1}{3}\)∙ a2 ∙ a = \(\frac{{{a^3}}}{3}\)
\[\frac{{{V_{SAMN}}}}{{{V_{SABD}}}} = \frac{{SN}}{{SD}}\cdot\frac{{SM}}{{SB}} = .\frac{{23}}{{12}} = \frac{1}{3}\]
Mà \({V_{SABD}} = \frac{1}{2}{V_{SABCD}} = \frac{1}{2}\cdot\frac{{{a^3}}}{3} = \frac{{{a^3}}}{6}\)
\( \Rightarrow {V_{SAMN}} = \frac{{{a^3}}}{{18}}\)
Ta lại có :
\[\begin{array}{l}{V_{NADC}} = \frac{1}{3}\cdot{S_{ADC}}\cdotd(N;(ADC)) = \frac{1}{3}\cdot{S_{ADC}}\cdot\frac{1}{3}d(S;(ADC)) = \frac{1}{3}{V_{SABD}} = \frac{1}{6}{V_{SABCD}} = \frac{{{a^3}}}{{18}}\\{V_{MABC}} = \frac{1}{3}\cdot{S_{ABC}}\cdotd(M;(ABC)) = \frac{1}{3}\cdot{S_{ABC}}\cdot\frac{1}{2}d(S;(ABC)) = \frac{1}{2}{V_{SABC}} = \frac{1}{4}{V_{SABCD}} = \frac{{{a^3}}}{{12}}\end{array}\]
Mặt khác:
\[\begin{array}{l}{V_{C.SMN}} = \frac{1}{3}d(C,(SMN)).{S_{\Delta SMN}} = \frac{1}{3}d(A,(SMN)).{S_{\Delta SMN}} = \frac{{{a^3}}}{{18}}\\\end{array}\]
Vậy:
\({V_{ACMN}} = {V_{S.ABCD}} - {V_{NSAM}} - {V_{NADC}} - {V_{MABC}} - {V_{SCMN}} = \frac{{{a^3}}}{3} - \frac{{{a^3}}}{{18}} - \frac{{{a^3}}}{{18}} - \frac{{{a^3}}}{{12}} - \frac{{{a^3}}}{{18}} = \frac{{{a^3}}}{{12}}\).
Câu 61:
Đa giác nào có số đường chéo bằng số cạnh?
 Xem đáp án
Xem đáp án
Gọi số cạnh của đa giác là n (n ≥ 3; n ∈ ℕ)
Số đường chéo của đa giác là: \[\frac{{n(n - 3)}}{2}\]
Theo đề bài ta có:
\[\frac{{n\left( {n - 3} \right)}}{2} = n\]
\[ \Leftrightarrow {n^2} - 3n = 2n\]
\[ \Leftrightarrow {n^2} - 5n = 0\]
\[\begin{array}{l} \Leftrightarrow n(n - 5) = 0\\ \Leftrightarrow \left[ \begin{array}{l}n = 0(ktm)\\n = 5(tm)\end{array} \right.\end{array}\]
Vậy đa giác thỏa mãn đề bài là ngũ giác.
Câu 62:
Cho hàm số y = f(x) có đạo hàm trên ℝ. Đồ thị hàm số y = f′(x) như hình vẽ bên. Hàm số g(x) = f(x) − \(\frac{{{x^3}}}{3}\) + x2 – x + 2 đạt cực đại tại?
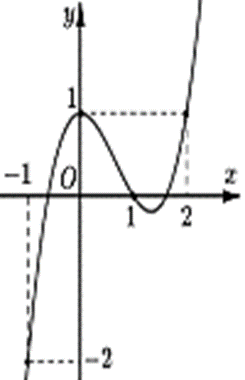
 Xem đáp án
Xem đáp án
Ta có g′(x) = f′(x) – x2 + 2x − 1; g′(x) = 0 ⇒ f′(x) = (x−1)2.
Suy ra số nghiệm của phương trình g′(x) = 0 chính là số giao điểm giữa đồ thị của hàm số f′(x) và parapol (P): y = (x−1)2.
Dựa vào đồ thị ta suy ra g′(x) = 0 \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = 2\end{array} \right.\)
Vậy g(x) đạt cực đại tại x = 1.
Câu 63:
 Xem đáp án
Xem đáp án
Gọi số tự nhiên có 5 chữ số là \(\overline {abcde} \).
Buộc 3 chữ số 1, 2, 3 thành 1 cụm, đặt là A
Hoán vị các chữ số 1, 2, 3 cho nhau ta được 3! = 6 khả năng xảy ra của A
Có 3 cách chọn vị trí cho A trong \(\overline {abcde} \)
Sau khi chọn xong vị trí cho A, 2 chữ số còn lại có \(A_7^2 = 42\) cách chọn
Như vậy, sẽ có 3 ∙ 6 ∙ 42 = 756 số được tạo thành tính cả trường hợp a = 0.
Xét a = 0:
Khi đó, ta có 2 vị trí cho A, và mỗi vị trí có 6 khả năng xảy ra của A (Hoán vị 1, 2, 3)
Chữ số còn lại có 6 cách chọn
Vậy nếu a = 0 thì sẽ có 72 số được tạo thành.
Vậy số số tự nhiên có 5 chữ số (a khác 0) thỏa mãn yêu cầu bài toán: 756 − 72 = 684 số tự nhiên.
Câu 64:
So sánh: \(2\sqrt {31} \) và 10.
 Xem đáp án
Xem đáp án
\[2\sqrt {31} = \sqrt {{2^2}.31} = \sqrt {4.31} = \sqrt {124} \]
Mà \(10 = \sqrt {100} \)
Vì \(\sqrt {124} > \sqrt {100} \Rightarrow 2\sqrt {31} > 10\).
Câu 65:
Tìm m để phương trình mx2 – 2(m + 1) – 2m – 2 = 0 có 2 nghiệm phân biệt?
 Xem đáp án
Xem đáp án
(ĐK 1) a ≠ 0 ⇒ m ≠ 0
(ĐK 2) ∆’ = (m + 1)2 + 2m (m + 1) > 0
⇒ (m + 1) (m + 1 + 2m) > 0
⇒ (m + 1) (3m + 1) > 0
\( \Rightarrow \left[ \begin{array}{l}m < - 1\\m > \frac{{ - 1}}{3}\end{array} \right.\)
Vậy với m ≠ 0, m < – 1, \(m > \frac{{ - 1}}{3}\) thì phương trình mx2 – 2(m + 1) – 2m – 2 = 0 có 2 nghiệm phân biệt.
Câu 66:
Tìm x biết: x + 45 − 25 = 32.
 Xem đáp án
Xem đáp án
x + 45 − 25 = 32
x + 45 = 32 + 25
x + 45 = 57
x = 57 − 45
x = 12
Vậy x = 12 thì x + 45 – 25 = 32.
Câu 67:
 Xem đáp án
Xem đáp án
3 = 3,0
\[\frac{1}{4} = \frac{{25}}{{100}} = 0,25\]
Câu 68:
Tìm hai số nguyên dương a, b biết BCNN (a, b) = 240 và ƯCLN (a, b) = 16. b – a là 32.
 Xem đáp án
Xem đáp án
ƯCLN (a, b) = 16
⇒ a =16k, b = 16q (k, q thuộc N, (k, q) = 1)
⇒ BCNN (a, b) = 240 = 16 ∙ k ∙ q
⇒ k ∙ q = 15 (1)
Lại có: b − a = 32
⇒ 16q − 16k = 32
⇒ 16 (q − k) = 32
⇒ q − k = 2 (2)
Từ (1) và (2) ⇒ k = 3, q = 5
⇒ a = 48, b = 80
Vậy a = 48, b = 80 tmđk.
Câu 69:
Một lớp học có 3 tổ học sinh cùng nhặt giấy vụn tổ 1 và tổ 2 thu nhập được 25,3 kg tổ 1 và tổ 3 nhặt được 36,2 kg tổ 2 và tổ 3 nhặt được 24,5 kg hỏi lớp đó thu nhặt được bao nhiêu kg giấy loại?
 Xem đáp án
Xem đáp án
Tổng số giấy vụn thu được là:
(25,3 + 36,2 + 24,5) : 2 = 43 (kg)
Tổ 1 thu được số giấy vụn là:
43 − 24,5 = 18,5 (kg)
Tổ 2 thu được số giấy vụn là:
43 − 36,2 = 6,8 (kg)
Tổ 3 thu được số giấy vụn là:
43 − 25,3 = 17,7 (kg)
Đáp số: Tổ 1: 18,5 kg
Tổ 2: 6,8 kg
Tổ 3: 17,7 kg.
