118 câu hỏi trắc nghiệm thuộc Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 85)

Câu 1:

Cho a + b + c = 2. Tìm giá trị lớn nhất của:

P = \frac{a b}{\sqrt{a b + 2 c}} + \frac{b c}{\sqrt{b c + 2 a}} + \frac{c a}{\sqrt{c a + 2 b}}

Xem đáp án

Theo BĐT Cauchy-Schwarz ta có:

$\frac{a b}{\sqrt{a b + 2 c}} = \frac{a b}{\sqrt{a b + (a + b + c) c}} = \frac{a b}{\sqrt{a b + a c + b c + c^{2}}} = \frac{a b}{\sqrt{(a + c) (b + c)}} \leq \frac{1}{2} (\frac{a b}{a + c} + \frac{a b}{b + c})$

Tương tự ta cũng có:

$\frac{b c}{\sqrt{b c + 2 a}} \leq \frac{1}{2} (\frac{b c}{a + b} + \frac{b c}{a + c})$

$\frac{c a}{\sqrt{c a + 2 b}} \leq \frac{1}{2} (\frac{c a}{a + b} + \frac{c a}{b + c})$

Cộng theo vế 3 BĐT trên ta có:

$P \leq \frac{1}{2} (\frac{a b + b c}{a + c} + \frac{b c + c a}{a + b} + \frac{a b + c a}{b + c})$

$= \frac{1}{2} (\frac{b (a + c)}{a + c} + \frac{c (a + b)}{a + b} + \frac{a (b + c)}{b + c}) = \frac{1}{2} (a + b + c) = \frac{1}{2} \cdot 2 = 1.$

Dấu “ = ” xảy ra khi $a = b = c = \frac{2}{3} .$

Câu 2:

Cho hàm số y = ax⁴ + bx²+ c có đồ thị như hình vẽ bên.

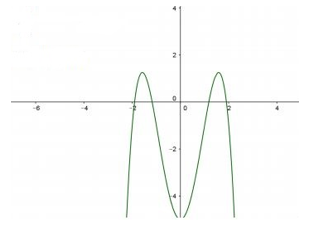
Media VietJack

Mệnh đề nào dưới đây đúng?

A. a > 0, b < 0, c > 0;

B. a < 0, b > 0, c < 0;

C. a < 0, b < 0, c < 0;

D. a > 0, b < 0, c < 0.

Xem đáp án

Đáp án đúng là: B

Nhánh ngoài cùng bên phải của hàm số bậc bốn trùng phương đi xuống nên a < 0.

Đồ thị hàm số bậc bốn trùng phương có ba cực trị nên a.b < 0 ⇒ b > 0

Do đồ thị cắt trục Oy tại điểm có tung độ âm nên c < 0

Vậy đáp án đúng là đáp án B.

Câu 3:

Cho hình hộp ABCD.A’B’C’D’ có chiều cao bằng 6, diện tích đáy bằng 8. Gọi M là trung điểm AB. Mặt phẳng (A’C’M) cắt BC tại N. Tính thể tích của khối đa diện có các đỉnh là D, M, N, A’, C’.

A. 10;

B. 18;

C. 12;

D. 24.

Xem đáp án

Đáp án đúng là: B

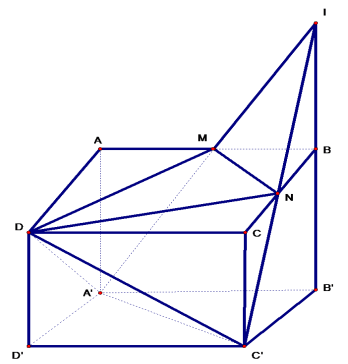
Trong mặt phẳng (ABB’A’) gọi I = BB’ ∩ A’M

Trong mặt phẳng (BCC’B’) gọi N = BC ∩ IC’

Gọi S, h lần lượt là diện tích đáy và chiều cao của khối hộp ABCD.A’B’C’D’.

Ta có $V_{I . A' B' C'} = \frac{1}{3} \cdot \frac{1}{2} \cdot S \cdot 2 h = \frac{1}{3} S . h$

V_{I . B M N} = \frac{1}{3} \cdot \frac{1}{8} \cdot S \cdot h = \frac{1}{24} S . h

\Rightarrow V_{1} = V_{B M N . B' A' C'} = \frac{1}{3} S h - \frac{1}{24} S h = \frac{7}{24} S h = \frac{7}{24} V

Ta có: $V_{2} = V_{D . D' A' C'} = \frac{1}{3} . \frac{1}{2} . S . h = \frac{1}{6} S h = \frac{1}{6} V$

Do đó: V_DMNC’A’ = V – V₁ – V₂– V₃ – V₄

$= V - \frac{7}{24} V - \frac{1}{6} = V - \frac{1}{12} V - \frac{1}{12} V = \frac{9}{24} V = 18$

Vậy đáp án đúng là B.

Câu 4:

Cho hình hộp ABCD.A’B’C’D’. Gọi M là điểm trên cạnh AC sao cho AC = 3MC. Lấy N trên cạnh C’D sao cho C’N = xC’D. Với giá trị nào của x thì MN // BD’.

A. $x = \frac{2}{3}$

B. $x = \frac{1}{3}$

C. $x = \frac{1}{4}$

D. $x = \frac{1}{2}$

Xem đáp án

Đáp án đúng là: A

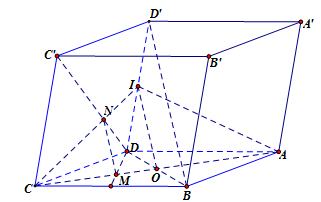
Ta có M là điểm trên cạnh AC sao cho AC = 3MC. Nên M là trọng tâm của tam giác BCD.

Gọi O và I lần lượt là trung điểm của AC và DD’. Khi đó ta có: BD’ // (IAC).

Trong (CDD’C’), gọi N” = CI ∩ C’D. Suy ra N’ là trọng tâm tam giác CDD’.

Do đó $\frac{C M}{C O} = \frac{2}{3} = \frac{C N'}{C I}$ ⇒ MN’ // OI, mà OI // BD’ nên MN’ // BD’

Vậy N’ ≡ N và x = $\frac{2}{3}$

Vậy đáp án đúng là A.

Câu 5:

Một hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước là 2 cm, 3 cm và 6 cm. Thể tích của khối tứ diện ACB’D’ bằng:

A. 12 cm³;

B. 8 cm³;

C. 6 cm³;

D. 4 cm³.

Xem đáp án

Đáp án đúng là: A

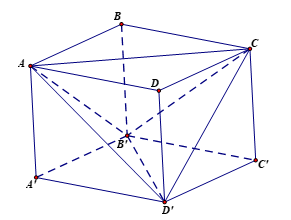
Thể tích khối hộp chữ nhật ABCD.A’B’C’D’ là: V = 2.3.6 = 36 (cm³).

Ta có: V_{A.A’B’D’} = V_{C.C’B’D’} = V_D’.DAC = V_B’.BAC = $\frac{1}{6}$ V

Vậy: V_ACB’D’ = V – (V_{A.A’B’D’}+ V_{C.C’B’D’}+ V_D’.DAC+ V_B’.BAC)

= $V - \frac{4}{6} V = \frac{1}{3} V = \frac{1}{3} \cdot 36 = 12$ (cm³)

Vậy đáp án đúng là đáp án A

Câu 6:

Cho tam giác ABC đều cạnh a. Gọi M là trung điểm BC. Khẳng định nào sau đây đúng?

A. $\vec{M B} = \vec{M C}$

B. $\vec{A M} = \frac{a \sqrt{3}}{2}$

C. $\vec{A M}$ = a

D. $|\vec{A M}| = \frac{a \sqrt{3}}{2}$

Xem đáp án

Đáp án đúng là: D

Ta có: $A M^{2} = \frac{A C^{2} + A B^{2}}{2} - \frac{B C^{2}}{4} = \frac{a^{2} + a^{2}}{2} - \frac{a^{2}}{4} = \frac{3 a}{4}$

$\Rightarrow A M = \frac{\sqrt{3} a}{2} \Rightarrow |\vec{A M}| = \frac{\sqrt{3} a}{2}$

Đáp án đúng là: D

Câu 7:

Chứng minh a² + b² + c² + 3 ≥ 2(a + b + c).

Xem đáp án

Ta có: a² + b² + c² + 3 ≥ 2(a + b + c)

⇔ a² + b² + c² + 3 – 2(a + b + c) ≥ 0

⇔ a² – 2a + 1 + b² – 2b + 1 + c² – 2c + 1 ≥ 0

⇔ (a – 1)² + (b – 1)² + (c – 1)² ≥ 0 (luôn đúng)

Vậy ta có điều phải chứng minh.

Câu 8:

Chứng minh rằng:

a) (a + b + c)² ≤ 3(a² + b² + c²)

Xem đáp án

a) Ta có: (a + b + c)² ≤ 3(a² + b² + c²)

⇔ a² + b² + c² + 2ab + 2ac + 2bc ≤ 3a²+ 3b² + 3c²

⇔ -2a² – 2b²– 2c² + 2ab + 2ac + 2bc ≤ 0

⇔ -(a – b)² – (b – c)²– (c – a)² ≤ 0 (đúng với mọi a, b, c)

Dấu “=” xảy ra khi a = b = c.

Câu 9:

b) (a + b)² ≤ 2(a² + b²)

Xem đáp án

b) (a + b)² ≤ 2(a² + b²)

⇔ a² – 2ab + b² ≤ 2a² + 2b²

⇔ –a² – 2ab – b² ≤ 0

⇔ –(a + b)² ≤ 0 (đúng với mọi a, b)

Dấu “=” xảy ra khi a = –b

Câu 10:

Tính tổng $S = C_{n}^{0} + C_{n}^{1} + ... + C_{n}^{n}$

A. S = 2ⁿ– 1;

B. S = 2ⁿ;

C. S = 2^n-1;

D. S = 2ⁿ + 1.

Xem đáp án

Đáp án đúng là: B

Xét khai triển: ${(x + 1)}^{n} = C_{n}^{0} . x^{n} {.1}^{0} + C_{n}^{1} . x^{n - 1} {.1}^{1} + C_{n}^{2} . x^{n - 2} {.1}^{2} + ... + C_{n}^{n} . x^{0} {.1}^{n}$

Thay x = 1 vào 2 vế, ta có:

${(1 + 1)}^{n} = C_{n}^{0} + C_{n}^{1} + C_{n}^{2} + ... + C_{n}^{n} \Leftrightarrow 2^{n} = S$

Vậy đáp án đúng là B.

Câu 11:

Cho phương trình x² – mx + m – 1 = 0 (m là tham số)

a) Giải phương trình với m = 3.

Xem đáp án

a) Thay m = 3 vào phương trình ta có:

x² – 3x + 3 – 1 = 0

Û x² – 3x + 2 = 0

Û x² – 2x – x + 2 = 0

Û x(x – 2) – (x – 2) = 0

Û (x – 1)(x – 2) = 0

$\Leftrightarrow [\begin{array}{l} x - 1 = 0 \\ x - 2 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 1 \\ x = 2 \end{array}$

Vậy khi m = 3 thì phương trình có tập nghiệm S = {1; 2}.

Câu 12:

b) Tìm tất cả các giá trị m để phương trình có 2 nghiêm x₁, x₂ thỏa mãn x₁– 2x₂ = 3.

Xem đáp án

b) D = (–m)² – 4.1.(m – 1) = m² – 4m+ 4 = (m – 2)² ≥ 0

⟹ Phương trình luôn có 2 nghiệm x₁; x₂

Khi đó theo hệ thức Vi-ét ta có: $\{\begin{cases} x_{1} + x_{2} = m (1) \\ x_{1} . x_{2} = m - 1 (2) \end{cases}$

Theo đề bài: x₁ – 2x₂ = 3 Û x₁ = 3 + 2x₂ (3)

Thay (3) vào (1) ta có: 3 + 2x₂ + x₂= m Û 3x₂ = m – 3 $\Leftrightarrow x_{2} = \frac{m - 3}{3}$

Thay $x_{2} = \frac{m - 3}{3}$ vào (3) ta có:

$x_{1} = 3 + 2 \cdot \frac{m - 3}{3}$

$\Leftrightarrow x_{1} = 3 + \frac{2 m - 6}{3}$

$\Leftrightarrow x_{1} = \frac{9 + 2 m - 6}{3}$

$\Leftrightarrow x_{1} = \frac{2 m + 3}{3}$

Thay $x_{1} = \frac{2 m + 3}{3}$ ; $x_{2} = \frac{m - 3}{3}$ vào (2) ta có:

$\frac{2 m + 3}{3} \cdot \frac{m - 3}{3} = m - 1$

$\Leftrightarrow \frac{(2 m + 3) (m - 3)}{9} = \frac{9 (m - 1)}{9}$

Û (2m+3)(m – 3) = 9(m – 1)

Û 2m2 – 6m + 3m – 9 = 9m – 9

Û 2m2 – 3m – 9 = 9m – 9

Û 2m2 – 12m = 0

Û 2m(m – 6) = 0

$\Leftrightarrow [\begin{array}{l} 2 m = 0 \\ m - 6 = 0 \end{array} \Leftrightarrow [\begin{array}{l} m = 0 \\ m = 6 \end{array}$

Vậy m ∈ {0; 6} là giá trị cần tìm.

Câu 13:

Giải phương trình: $\sqrt{3 + x} + \sqrt{6 - x} = 3 + \sqrt{(3 + x) . (6 - x)} .$

Xem đáp án

Đặt $t = \sqrt{3 + x} + \sqrt{6 - x}$ $(t \geq 0)$

$\Leftrightarrow t^{2} = 9 + 2 \sqrt{(x + 3) (6 - x)}$

$\Leftrightarrow \sqrt{(x + 3) (6 - x)} = \frac{t^{2} - 9}{2}$

$\Leftrightarrow t = 3 + \frac{t^{2} - 9}{2} \Leftrightarrow 2 t = 6 + t^{2} - 9$

$\Leftrightarrow t^{2} - 2 t - 3 = 0$

$\Leftrightarrow [\begin{array}{l} t = - 1 (k t m) \\ t = 3 (t m) \end{array}$

$\Rightarrow \sqrt{(x + 3) (6 - x)} = \frac{3^{2} - 9}{2} = 0 \Leftrightarrow [\begin{array}{l} x = 6 \\ x = - 3 \end{array}$

Câu 14:

Giải phương trình x² – 2nx – 5 = 0. Biết số nguyên dương n thỏa mãn: $C_{n}^{n - 1} + C_{5}^{n} = 9$ .

A. $x = 4 \pm \sqrt{21}$ ;

B. x = ±4;

C. $x = 4 \pm \sqrt{2}$

D. $x = 2 \pm \sqrt{5}$

Xem đáp án

Đáp án đúng là: A

Xét phương trình: $C_{n}^{n - 1} + C_{5}^{n} = 9 \Leftrightarrow n = 4$

Với n = 4 thì phương trình trở thành: x² – 8x – 5 = 0

Vậy phương trình có hai nghiệm: $x = 4 \pm \sqrt{21}$

Đáp án đúng là A.

Câu 15:

Phương trình 3^2x+1 – 4.3^x + 1 = 0 có nghiệm x₁, x₂với x₁< x₂. Chọn phát biểu đúng?

A. x₁.x₂ = –1;

B. 2x₁ + x₂= 0;

C. x₁+ 2x₂= –1;

D. x₁+ x₂= 2.

Xem đáp án

Đáp án đúng là: C

3^2x+1 – 4.3^x + 1 = 0

⇔ 3.3^2x – 4.3^x + 1 = 0

$\Leftrightarrow [\begin{array}{l} x^{x} = 1 \\ 3^{x} = \frac{1}{3} \end{array} \Leftrightarrow [\begin{array}{l} x = 1 = x_{1} \\ x = 0 = x_{2} \end{array}$

⇒ x₁+ 2x₂= –1

Đáp án đúng là C

Câu 16:

Giải phương trình: log₂x.log₂(2x) – 2 = 0

Xem đáp án

ĐKXĐ: x > 0

log₂x.log₂(2x) – 2 = 0

⇔ log₂x . (log₂2 + log₂x) – 2 = 0

⇔ log₂x + log₂x. log₂x – 2 = 0

Đặt log₂x = t, ta có: t + t²– 2 = 0 ⇔ (t + 1)(t – 2) = 0

\Leftrightarrow [\begin{array}{l} t + 1 = 0 \\ t - 2 = 0 \end{array} \Leftrightarrow [\begin{array}{l} t = - 1 \\ t = 2 \end{array} \Leftrightarrow [\begin{array}{l} \log_{2} x = - 1 \\ \log_{2} x = 2 \end{array} \Leftrightarrow [\begin{array}{l} x = 2^{- 1} = \frac{1}{2} (T M) \\ x = 2^{2} = 4 (T M) \end{array}

Câu 17:

Một học sinh muốn chọn 20 trong 30 câu trắc nghiệm. Học sinh đó đã chọn được 5 câu. Tìm số cách chọn các câu còn lại?

A. $C_{30}^{15}$

B. $Α_{30}^{15}$

C. $C_{30}^{5}$

D. $C_{25}^{15}$

Xem đáp án

Đáp án đúng là: D

Trong 30 câu đã chọn 5 câu nên còn lại 25 câu.

Ta cần chọn 15 câu trong 25 câu nên có $C_{25}^{15}$ cách chọn.

Vậy đáp án đúng là D.

Câu 18:

Tổng các nghiệm của phương trình

\log_{2} (5 - 2^{x}) = 2 - x

bằng:

A. 3;

B. 1;

C. 2;

D. 0.

Xem đáp án

Đáp án đúng là: C

$\log_{2} (5 - 2^{x}) = 2 - x \Leftrightarrow 5 - 2^{x} = 2^{2 - x} \Leftrightarrow 5 - 2^{x} = \frac{4}{2^{x}}$

$\Leftrightarrow {5.2}^{x} - {(2^{x})}^{2} = 4 \Leftrightarrow [\begin{array}{l} 2^{x} = 4 \\ 2^{x} = 1 \end{array} \Leftrightarrow [\begin{array}{l} x = 2 \\ x = 0 \end{array}$

Vậy tổng các nghiệm của phương trình bằng 2

Đáp án đúng là C.

Câu 19:

Phương trình $\log_{x} 2 + \log_{2} x = \frac{5}{2}$

A. Vô nghiệm;

B. Có một nghiệm âm;

C. Có một nghiệm âm và một nghiệm dương;

D. Có hai nghiệm dương.

Xem đáp án

Đáp án đúng là: C

ĐKXĐ: x >0

$\log_{x} 2 + \log_{2} x = \frac{5}{2} \Leftrightarrow \frac{1}{\log_{2} x} + \log_{2} x = \frac{5}{2}$

Đặt log₂x = t

$\Rightarrow \frac{1}{t} + t = \frac{5}{2}$

$\Rightarrow 2 t^{2} - 5 t + 2 = 0$

$\Rightarrow (t - 2) (2 t - 1) = 0$

$\Rightarrow t \in \{2, \frac{1}{2}\}$

$\Rightarrow l o g_{2} x \in \{2, \frac{1}{2}\}$

⇒ x ∈ {1; –1}

Vậy đáp án đúng là C.

Câu 20:

Phương trình $4^{x^{2} + 2} = 16$ có số nghiệm là

A. 1;

B. 2;

C. 3;

D. 4.

Xem đáp án

Đáp án đúng là: A

$4^{x^{2} + 2} = 16 = 4^{2} \Leftrightarrow x^{2} + 2 = 2 \Leftrightarrow x = 0$

Vậy phương trình có nghiệm duy nhất x = 0.

Đáp án đúng là A.

Câu 21:

Số nghiệm thực của phương trình $4^{x - 1} + 2^{x + 3} - 4 = 0$ là:

A. 1;

B. 2;

C. 3;

D. 0.

Xem đáp án

Đáp án đúng là: A

$4^{x - 1} + 2^{x + 3} - 4 = 0 \Leftrightarrow \frac{1}{4} {.2}^{2 x} + {8.2}^{x} - 4 = 0$

$\Leftrightarrow [\begin{array}{l} 2^{x} = - 16 + 4 \sqrt{17} (T M) \\ 2^{x} = - 16 - 4 \sqrt{17} (K T M) \end{array} \Leftrightarrow x = \log_{2} (4 \sqrt{17} - 6)$

Vậy phương trình đã cho có 1 nghiệm.

Đáp án đúng là A.

Câu 22:

Trong hệ trục tọa độ Oxy cho hình bình hành OABC, điểm C thuộc trục hoành. Khẳng định nào sau đây đúng?

A. $\vec{A B}$ có tung độ khác 0;

B. Hai điểm A, B có tung độ khác nhau;

C. C có hoành độ bằng 0;

D. x_A+ x_C– x_B= 0

Xem đáp án

Đáp án đúng là: D

Vì OABC là hình bình hành nên: $\vec{A B} = \vec{O C}$

Û x_B– x_A= x_C⇔ x_A+ x_C– x_B= 0

Vậy đáp án đúng là đáp án D.

Câu 23:

Trong mặt phẳng với hệ tọa độ Oxy cho hình bình hành OABC có tọa độ điểm A(3; 1), C(–1; 2) (tham khảo hình vẽ bên).

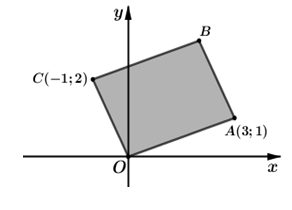
Media VietJack

Số phức nào sau đây có điểm biểu diễn là điểm B?

A. z₁= –2 + 3i;

B. z₂= 2 + 3i;

C. z₃= 4 – i;

D. z₄= –4 + i.

Xem đáp án

Đáp án đúng là: B

Vì OABC là hình bình hành nên:

$\vec{O A} = \vec{B C} \Rightarrow \{\begin{cases} x_{A} - 0 = x_{B} - x_{C} \\ y_{A} - 0 = y_{B} - y_{C} \end{cases} \Rightarrow \{\begin{cases} x_{B} = 2 \\ y_{B} = 3 \end{cases}$

Suy ra số phức z₂ = 2 + 3i có điểm biểu diễn là B.

Đáp án đúng là B.

Câu 24:

Trong hệ tọa độ Oxy, cho ba điểm A(1; 3); B(–1; 2); C(–2; 1). Tìm tọa độ của vectơ $\vec{A B} - \vec{A C}$

A. (–5; –3);

B. (1; 1);

C. (–1; 2);

D. (–1; 1).

Xem đáp án

$\{\begin{cases} \vec{A B} = (- 2; - 1) \\ \vec{A C} = (- 3; - 2) \end{cases} \Rightarrow \vec{A B} - \vec{A C} = (- 2 - (- 3); - 1 - (- 2)) = (1; 1)$

Vậy đáp án đúng là B.

Câu 25:

Trong hệ tọa độ Oxy, cho ba điểm A(1; 1); B(2; –1); C(4; 3). Tọa độ điểm D để ABDC là hình bình hành là

A. D(1; 3);

B. D(3; 5);

C. D(3; 1);

D. D(5; 1).

Xem đáp án

Đáp án đúng là: D

Gọi D(x; y) $\Rightarrow \vec{C D} = (x - 4; y - 3); \vec{A B} = (1; - 2)$

Để ABCD là hình bình hành thì $\vec{A B} = \vec{C D}$

$\Leftrightarrow \{\begin{cases} x - 4 = 1 \\ y - 3 = - 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 5 \\ y = 1 \end{cases}$ nên D(5; 1)

Vậy đáp án đúng là D.

Câu 26:

Tìm số hạng chứa x trong khai triển ${(1 + 2 \sqrt{x} - 3 \sqrt[3]{x})}^{4}$ .

A. 144x;

B. –72x;

C. –84x;

D. 132x.

Xem đáp án

Đáp án đúng là: C

Ta có: ${(1 + 2 \sqrt{x} - 3 \sqrt[3]{x})}^{4} = \sum_{k = 0}^{4} C_{4}^{k} {.1}^{4 - k} . {(2 \sqrt{x} - 3 \sqrt[3]{x})}^{k}$

$= \sum_{k = 0}^{4} C_{4}^{k} . \sum_{m = 0}^{k} C_{k}^{m} {(2 \sqrt{x})}^{m} {(- 3 \sqrt[3]{x})}^{k - m}$

$= \sum_{k = 0}^{4} C_{4}^{k} . \sum_{m = 0}^{k} C_{k}^{m} {.2}^{m} . x^{\frac{m}{2}} . {(- 3)}^{k - m} x^{\frac{k - m}{3}}$ $(m \leq k \leq 4, m \in ℕ)$

$= \sum_{k = 0}^{4} C_{4}^{k} . \sum_{m = 0}^{k} C_{k}^{m} {.2}^{m} . {(- 3)}^{k - m} . x^{\frac{m}{2} + \frac{k - m}{3}}$

Số hạng chứa x trong khai triển là $x^{\frac{m}{2} + \frac{k - m}{3}} = x$

Khi đó $\frac{m}{2} + \frac{k - m}{3} = 1$ $\Leftrightarrow 3 m + 2 k - 2 m = 6 \Leftrightarrow m = 6 - 2 k$

Mà $m \leq k \leq 4$ nên $6 - 2 k \leq k \leq 4$ $\Rightarrow k \in \{2; 3; 4\}$

Với $k = 2 \Rightarrow m = 2$

Với $k = 3 \Rightarrow m = 0$

Với $k = 4 \Rightarrow m = - 2 (k t m)$

Khi đó hệ số của số hạng chứa x là $C_{4}^{2} C_{2}^{2} {.2}^{2} . {(- 3)}^{2 - 2} + C_{4}^{3} C_{3}^{0} {.2}^{0} . {(- 3)}^{3 - 0} = - 84$

Vậy số hạng cần tìm là –84x.

Câu 27:

Tìm x biết: x³ + 27 + (x + 3)(x – 9) = 0.

Xem đáp án

x³ + 27 + (x + 3)(x - 9) = 0

⇔ x³+ 3³ + (x + 3)(x - 9) = 0

⇔ (x + 3)(x² – 3x + 9) + (x + 3)(x - 9) = 0

⇔ (x + 3)(x² – 3x + 9 + x - 9) = 0

⇔ (x + 3)( x² – 2x) = 0

⇔ x.(x + 3).(x – 2) = 0

$\Leftrightarrow [\begin{array}{l} x = 0 \\ x + 3 = 0 \\ x - 2 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = - 3 \\ x = 2 \end{array}$

Vậy $x \in \{0; - 3; 2\}$ .

Câu 28:

Gọi X là tập hợp các số tự nhiên gồm 6 chữ số đôi một khác nhau được tạo thành từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên một số từ tập hợp X. Tính xác suất để số được chọn chỉ chứa 3 chữ số lẻ.

Xem đáp án

Gọi Ω là không gian mẫu của phép thử: “Chọn ngẫu nhiên một số từ tập X”

Khi đó $|Ω| = Α_{9}^{6} = 60 480$

Gọi A là biến cố: “Số được chọn chỉ chứa 3 chữ số lẻ”. Khi đó:

+ Chọn 3 chữ số lẻ đôi một khác nhau từ các chữ số 1; 3; 5; 7; 9 có $C_{5}^{3}$ cách

+ Chọn 3 chữ số chẵn đôi một khác nhau từ các chữ số 2; 4; 6; 8 có $C_{4}^{3}$ cách

+ Sắp xếp các chữ số trên để được số thỏa mãn biến cố A có 6! cách

Do đó $|Ω_{A}| = C_{5}^{3} . C_{4}^{3} .6! = 28 800$

Vậy xác suất cần tìm là: $P (A) = \frac{|Ω_{A}|}{|Ω|} = \frac{28800}{60480} = \frac{10}{21}$

Câu 29:

a) Tìm các ước của mỗi số sau: 2, 3, 4, 5, 6, 7, 17, 34.

Xem đáp án

a) Các ước của 2 là: 1; 2

Các ước của 3 là: 1; 3

Các ước của 4 là: 1; 2; 4

Các ước của 5 là: 1; 5

Các ước của 6 là: 1; 2; 3; 6

Các ước của 7 là: 1; 7

Các ước của 34 là: 1; 2; 17; 34.

Câu 30:

b) Trong các số trên, những số nào có hai ước, những số nào có nhiều hơn hai ước?

Xem đáp án

b) Các số 2, 3, 5, 7, 17 chỉ có hai ước là 1 và chính nó. Các số đó được gọi là số nguyên tố.

Các số 4, 6, 34 có nhiều hơn hai ước. Các số đó được gọi là hợp số.

Câu 31:

Số lượng các nghiệm của bất phương trình $\frac{1}{C_{n}^{1}} - \frac{1}{C_{n + 2}^{2}} > \frac{7}{6 C_{n + 4}^{1}}$ .

A. 9;

B. 11;

C. 12;

D. 10.

Xem đáp án

Đáp án đúng là: B

Ta có: $\frac{1}{C_{n}^{1}} - \frac{1}{C_{n + 2}^{2}} > \frac{7}{6 C_{n + 4}^{1}}$ $(n \geq 1, n \in ℕ)$

$\Leftrightarrow \frac{1}{\frac{n!}{1! (n - 1)!}} - \frac{1}{\frac{(n + 2)!}{2! (n + 2 - 2)!}} > \frac{7}{6 \frac{(n + 4)!}{1! (n + 4 - 1)!}}$

\Leftrightarrow \frac{1}{n} - \frac{1}{\frac{(n + 2) (n + 1)}{2}} > \frac{7}{6 (n + 4)}

\Leftrightarrow \frac{1}{n} - \frac{2}{(n + 2) (n + 1)} > \frac{7}{6 (n + 4)}

\Leftrightarrow \frac{6 (n + 4) (n + 2) (n + 1) - 2 n .6 (n + 4) - 7 n (n + 2) (n + 1)}{6 n (n + 2) (n + 1) (n + 4)} > 0

\Leftrightarrow (6 n + 24) (n^{2} + 3 n + 2) - 12 n^{2} - 48 n - 7 n (n^{2} + 3 n + 2) > 0

\Leftrightarrow 6 n^{3} + 18 n^{2} + 12 n + 24 n^{2} + 72 n + 48 - 12 n^{2} - 48 n - 7 n^{3} - 21 n^{2} - 14 n > 0

\Leftrightarrow - n^{3} + 9 n^{2} + 22 n + 48 > 0

Xét $n = 12$ ta có $V T = - 12^{3} + {9.12}^{2} + 22.12 + 48 = - 120 < 0$

Xét $n = 11$ ta có $V T = - 11^{3} + {9.11}^{2} + 22.12 + 48 = 48 > 0$

Do đó $1 \leq n \leq 11$ và $n \in ℕ$ nên $n \in \{1; 2; 3; ...; 11\}$

Vậy có 11 giá trị thỏa mãn.

Câu 32:

Phân tích đa thức thành nhân tử: (x – y)² + 4(x – y) – 12.

Xem đáp án

(x – y)² + 4(x – y) – 12

= (x – y)²+ 4(x – y) + 4 – 16

= (x – y)²+ 2(x – y).2 + 2² – 16

= (x – y + 2)² – 4²

= (x – y + 2 − 4)(x – y + 2 + 4)

= (x – y – 2)(x – y + 6)

Câu 33:

Giải phương trình: (x + 1)(x² – x + 1) – 2x = x(x – 1)(x + 1).

Xem đáp án

(x + 1)(x² – x + 1) – 2x = x(x – 1)(x + 1)

⇔ x³ + 1 – 2x = x(x² – 1)

⇔ x³ + 1 – 2x = x³– x

⇔ x³ – x³– 2x + x = –1

⇔ –x = –1

⇔ x = 1

Vậy nghiệm của phương trình là x = 1

Câu 34:

Giải phương trình: $\frac{2}{x - 1} = \frac{1 + 2 x}{x + 2}$

Xem đáp án

$\frac{2}{x - 1} = \frac{1 + 2 x}{x + 2}$

⇔ 2(x + 2) = (x – 1)(2x + 1)

⇔ 2x + 4 = 2x² – 1

⇔ 2x² – 3x – 5 = 0

$\begin{array}{l} \Leftrightarrow x^{2} - \frac{3}{2} x - \frac{5}{2} = 0 \\ \Leftrightarrow x^{2} - 2 x . \frac{3}{4} + \frac{9}{16} - \frac{49}{16} = 0 \\ \Leftrightarrow {(x - \frac{3}{4})}^{2} - \frac{49}{16} = 0 \\ \Leftrightarrow {(x - \frac{3}{4})}^{2} = {(\frac{7}{4})}^{2} \\ \Leftrightarrow [\begin{array}{l} x - \frac{3}{4} = \frac{7}{4} \\ x - \frac{3}{4} = \frac{- 7}{4} \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{5}{2} \\ x = - 1 \end{array} \end{array}$

Vậy nghiệm của phương trình là: $\{\frac{5}{2}; - 1\}$ .

Câu 35:

Cho a, b > 0 thỏa mãn $\frac{1}{a^{2}} + \frac{1}{b^{2}} = 2$ . Chứng minh a + b ≥ 2.

Xem đáp án

Ta có: $2 = \frac{1}{a^{2}} + \frac{1}{b^{2}} = \frac{a^{2} + b^{2}}{{(a b)}^{2}} \geq \frac{{(a + b)}^{2}}{2 {(\frac{{(a + b)}^{2}}{4})}^{2}}$

\Rightarrow {(a + b)}^{2} \geq 4

Dấu “ = ” xảy ra khi a = b = 1 ⇔ a + b = 1 + 1 = 2

Câu 36:

Chứng minh rằng: $\frac{1}{a^{2}} + \frac{1}{b^{2}} + 2 \geq \frac{8}{a + b}$

Xem đáp án

Ta có:

$\begin{array}{l} \frac{1}{a^{2}} + \frac{1}{b^{2}} \geq 2 \cdot \frac{1}{a} \cdot \frac{1}{b} \\ \Leftrightarrow 2 (\frac{1}{a^{2}} + \frac{1}{b^{2}}) \geq \frac{1}{a^{2}} + \frac{1}{b^{2}} + 2 \cdot \frac{1}{a} \cdot \frac{1}{b} \\ \Leftrightarrow 2 (\frac{1}{a^{2}} + \frac{1}{b^{2}}) \geq {(\frac{1}{a} + \frac{1}{b})}^{2} (1) \end{array}$

Mặt khác:

$\begin{array}{l} {(\frac{1}{a} + \frac{1}{b} - 2)}^{2} \geq 0 \\ \Leftrightarrow {(\frac{1}{a} + \frac{1}{b})}^{2} - 4 (\frac{1}{a} + \frac{1}{b}) + 4 \geq 0 \\ \Leftrightarrow {(\frac{1}{a} + \frac{1}{b})}^{2} + 4 \geq 4 (\frac{1}{a} + \frac{1}{b}) (2) \end{array}$

Lại có: (a + b)² ≥ 4ab

\Leftrightarrow \frac{a + b}{a b} \geq \frac{4}{a + b} \Leftrightarrow \frac{1}{a} + \frac{1}{b} \geq \frac{4}{a + b} (3)

Từ (1), (2), (3) ⇒ $2 (\frac{1}{a^{2}} + \frac{1}{b^{2}}) + 4 \geq {(\frac{1}{a} + \frac{1}{b})}^{2} + 4 \geq 4 (\frac{1}{a} + \frac{1}{b}) \geq \frac{16}{a + b}$

$\Leftrightarrow \frac{1}{a^{2}} + \frac{1}{b^{2}} + 2 \geq \frac{8}{a + b}$ (với a, b > 0)

Câu 37:

Cho 3 số dương a, b, c thỏa mãn: a + b + c + ab + ca + bc = 6abc.

Chứng minh rằng: $\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \geq 3$ .

Xem đáp án

Từ a + b + c + ab + ca + bc = 6abc ta có: $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{a b} + \frac{1}{b c} + \frac{1}{c a} = 6$

Ta có: $\frac{1}{a^{2}} + 1 \geq \frac{2}{a}; \frac{1}{b^{2}} + 1 \geq \frac{2}{b}; \frac{1}{c^{2}} + 1 \geq \frac{2}{c}$

Và $\frac{1}{a^{2}} + \frac{1}{b^{2}} \geq \frac{2}{a b}; \frac{1}{b^{2}} + \frac{1}{c^{2}} \geq \frac{2}{b c}; \frac{1}{a^{2}} + \frac{1}{c^{2}} \geq \frac{2}{a c}$

Cộng các vế các BĐT trên ta có:

$\begin{array}{l} 3 (\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} + 1) \geq 2 (\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{a b} + \frac{1}{b c} + \frac{1}{c a}) \\ \Leftrightarrow 3 (\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} + 1) \geq 12 \\ \Leftrightarrow \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} + 1 \geq 4 \\ \Leftrightarrow \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \geq 3 \end{array}$

Dấu “ = ” xảy ra khi a = b = c = 1

Câu 38:

Thực hiện phép tính: (4x – 1)(2x² – x – 1).

Xem đáp án

(4x – 1)(2x² – x – 1)

= 8x³ – 4x² – 4x – 2x²+ x + 1

= 8x³ – 6x² – 3x + 1.

Câu 39:

Rút gọn biểu thức:

P = (\frac{3 \sqrt{x}}{\sqrt{x} + 2} + \frac{\sqrt{x}}{\sqrt{x} - 2} - \frac{x - \sqrt{x}}{x - 4}) : \frac{3 \sqrt{x}}{\sqrt{x} + 2}

với x > 0, x ≠ 4

A. $P = \frac{\sqrt{x} - 1}{\sqrt{x} - 2}$

B. $P = \frac{\sqrt{x} + 1}{\sqrt{x} - 2}$

C. $P = \frac{\sqrt{x} - 1}{\sqrt{x} + 2}$

D. $P = \frac{\sqrt{x} - 1}{\sqrt{x} - 6}$

Xem đáp án

Đáp án đúng là: A

ĐKXĐ: x > 0, x ≠ 4.

$\begin{array}{l} P = (\frac{3 \sqrt{x}}{\sqrt{x} + 2} + \frac{\sqrt{x}}{\sqrt{x} - 2} - \frac{x - \sqrt{x}}{x - 4}) : \frac{3 \sqrt{x}}{\sqrt{x} + 2} \\ = (\frac{3 \sqrt{x}}{\sqrt{x} + 2} + \frac{\sqrt{x}}{\sqrt{x} - 2} - \frac{x - \sqrt{x}}{(\sqrt{x} + 2) (\sqrt{x} - 2)}) : \frac{3 \sqrt{x}}{\sqrt{x} + 2} \\ = (\frac{3 \sqrt{x} (\sqrt{x} - 2) + \sqrt{x} (\sqrt{x} + 2) - x + \sqrt{x}}{(\sqrt{x} + 2) (\sqrt{x} - 2)}) : \frac{3 \sqrt{x}}{\sqrt{x} + 2} \\ = (\frac{3 x - 6 \sqrt{x} + x + 2 \sqrt{x} - x + \sqrt{x}}{(\sqrt{x} + 2) (\sqrt{x} - 2)}) \cdot \frac{\sqrt{x} + 2}{3 \sqrt{x}} \\ = \frac{3 x - 3 \sqrt{x}}{\sqrt{x} - 2} \cdot \frac{1}{3 \sqrt{x}} = \frac{3 \sqrt{x} (\sqrt{x} - 1)}{3 \sqrt{x} (\sqrt{x} - 2)} = \frac{\sqrt{x} - 1}{\sqrt{x} - 2} \end{array}$

Vậy đáp án đúng là A.

Câu 40:

Tập nghiệm S của bất phương trình $(x - 3) \sqrt{x - 2} \geq 0$ là:

A. S = [3; +∞);

B. S = (3; +∞);

C. S = {2} ∪ [3; +∞);

D. S = {2} ∪ (3; +∞).

Xem đáp án

Đáp án đúng là: C

ĐKXĐ: x ≥ 2.

Bất phương trình tương đương với $[\begin{array}{l} \sqrt{x - 2} = 0 \\ x - 3 \geq 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 2 \\ x \geq 3 \end{array}$

Vậy đáp án đúng là C.

Câu 41:

Cho giá trị gần đúng $\frac{3}{7}$ là 0,429. Sai số tuyệt đối của số 0,429 là:

A. 0,0001;

B. 0,0003;

C. 0,0005;

D. 0,0006.

Xem đáp án

Đáp án đúng là: C

Ta có: $\frac{3}{7}$ = 0,428571... nên sai số tuyệt đối của 0,429 là:

$Δ = |0, 429 - \frac{3}{7}| < |0, 429 - 0, 4285| = 0, 0005$

Vậy đáp án đúng là C.

Câu 42:

Chứng minh: $\frac{1}{3} + \frac{1}{3^{2}} + \frac{1}{3^{3}} + ... + \frac{1}{3^{99}} < \frac{1}{2}$

Xem đáp án

Đặt: A = $\frac{1}{3} + \frac{1}{3^{2}} + \frac{1}{3^{3}} + ... + \frac{1}{3^{99}} (1)$

\Rightarrow 3 A = 1 + \frac{1}{3} + \frac{1}{3^{2}} + ... + \frac{1}{3^{98}} (2)

Lấy (2) – (1) $\Rightarrow 2 A = 1 - \frac{1}{3^{99}} < 1$

$\Rightarrow A < \frac{1}{2}$ (đpcm)

Câu 43:

Độ dài đường sinh của một hình nón bằng 2a. Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng 120° Diện tích toàn phần của hình nón là:

A. $2 π a^{2} (3 + \sqrt{3})$

B. $π a^{2} (3 + 2 \sqrt{3})$

C. $6 π a^{2}$

D. $π^{2} (3 + \sqrt{3})$

Xem đáp án

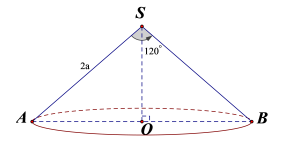
Chọn hình nón đỉnh S, đường tròn tâm O đường kính đáy AB như hình vẽ.

Ta có: l = SA = 2a và $\hat{A S B} = 120 °$ nên $\hat{A S O} = 60 °$

Xét ∆SOA vuông tại O ta có: OA = SA.sin 60^o = $a \sqrt{3}$

Diện tích toàn phần của hình nón:

$S_{t p} = π R^{2} + π R l = π . O A (O A + S A) = \sqrt{3} π a (a \sqrt{3} + 2 a) = π a^{2} (3 + 2 \sqrt{3})$

Vậy đáp án đúng là B.

Câu 44:

Đồ thị hàm số nào dưới đây nhận trục tung làm trục đối xứng?

A. y = sin x – cos x;

B. y = 2sin x;

C. y = 2sin (–x);

D. y = –2cos x.

Xem đáp án

Đáp án đúng là: D

Hàm số đó phải là hàm chẵn.

Xét y = –2cos x, có y(–x) = y(x) nên hàm D là hàm chẵn

Vậy đáp án đúng là đáp án D

Câu 45:

Một hộp đựng 9 viên bi trong đó có 4 viên bi màu đỏ, 5 viên bi màu xanh. Lấy ngẫu nhiên 3 viên bi. Tính xác suất để trong 3 viên bi lấy được có ít nhất 2 viên bi màu xanh.

Xem đáp án

Gọi A là biến cố lấy được ít nhất 2 viên bi xanh

TH1: Trong 3 viên bi lấy được có 2 viên bi xanh, 1 viên bi đỏ: có $C_{5}^{2} . C_{4}^{1} = 40$ cách

TH2: Ba viên bi lấy ra toàn màu xanh: có $ℂ_{5}^{3} = 10$ cách

Suy ra $n (A) = C_{5}^{2} . C_{4}^{1} + C_{5}^{3} = 50$

Vậy $P (A) = \frac{n (A)}{n (Ω)} = \frac{50}{54} = \frac{25}{27}$

Câu 46:

Một hộp đựng 5 bi đỏ, 2 bi đen và 4 bi trắng. Lấy ngẫu nhiên 2 bi từ trong hộp

a) Tính xác suất để được 2 bi khác màu

Xem đáp án

Không gian mẫu: $C_{11}^{2}$

a) Số cách lấy ra 2 viên cùng màu: $C_{5}^{2} + C_{2}^{2} + C_{4}^{2}$

Số cách lấy ra 2 viên khác màu: $C_{11}^{2} - (C_{5}^{2} + C_{2}^{2} + C_{4}^{2})$

Xác suất để được 2 bi khác màu: $P = \frac{C_{11}^{2} - (C_{5}^{2} + C_{2}^{2} + C_{4}^{2})}{C_{11}^{2}} = \frac{38}{55}$

Câu 47:

b) Tính xác suất để được ít nhất 1 bi đỏ.

Xem đáp án

b) Số cách lấy ra 2 viên không có bi đỏ nào: $C_{6}^{2}$

Số cách lấy ra ít nhất 1 bi đỏ: $C_{11}^{2} - C_{6}^{2}$

Xác suất để được ít nhất 1 bi đỏ: $P = \frac{C_{11}^{2} - C_{6}^{2}}{C_{11}^{2}} = \frac{40}{55}$

Câu 48:

Nếu lấy 3,14 làm giá trị gần đúng của π thì sai số tuyệt đối là:

A. 0,001;

B. 0,002;

C. 0,003;

D. 0,01.

Xem đáp án

Đáp án đúng là: A

Ta có số đúng π = 3,141… nên sai số tuyệt đối của số gần đúng 3,14 là:

∆ = |3,14 – π| < |3,141 – 3,14| = 0,001.

Vậy sai số tuyệt đối của số gần đúng 3,14 là 0,001.

Đáp án đúng là A.

Câu 49:

Tính diện tích của mặt cầu ngoại tiếp hình tứ diện đều cạnh a.

$A . \frac{2 π a^{2}}{3};$

$B . \frac{3 π a^{2}}{2};$

$C . \frac{3 π a^{2}}{4};$

$D . \frac{4 π a^{2}}{3} .$

Xem đáp án

Đáp án đúng là: B

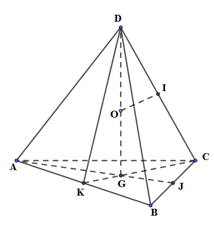
Xét tứ diện ABCD có cạnh đều bằng a. Gọi G là tâm tam giác ABC, I và J lần lượt là trung điểm của CD, BC

$\Rightarrow \{\begin{cases} D G ⊥ (A B C) \\ C G = \frac{2}{3} C K = \frac{2}{3} \cdot \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{3} \end{cases}$

Dựng mặt trung trực của CD, cắt DG tại O. Khi đó O là tâm mặt cầu ngoại tiếp tứ diện ABCD.

∆DGC vuông tại G $\Rightarrow D G = \sqrt{D C^{2} - G C^{2}} = \sqrt{a^{2} - \frac{a^{2}}{3}} = \frac{\sqrt{6} a}{3}$

∆DOI đồng dạng với ∆DCG

$\Rightarrow \frac{O D}{D C} = \frac{D I}{D G} \Rightarrow \frac{O D}{a} = \frac{\frac{a}{2}}{\frac{a \sqrt{6}}{3}} \Rightarrow O D = \frac{3 a}{2 \sqrt{6}} = \frac{a \sqrt{6}}{4} \Rightarrow R = \frac{a \sqrt{6}}{4}$

Diện tích mặt cầu là: $S_{m c} = 4 π R^{2} = 4 π {(\frac{a \sqrt{6}}{4})}^{2} = \frac{3}{2} π a^{2}$

Vậy đáp án đúng là B

Câu 50:

Phương trình $4 x^{\log_{8} x} + x^{\log_{8} 4 x} = 4$ có tập nghiệm là

A. {2;8}

B. $\{\frac{1}{2}; 8\}$

C. $\{\frac{1}{2}; \frac{1}{8}\}$

D. $\{2; \frac{1}{8}\}$

Xem đáp án

Đáp án đúng là: D

Điều kiện: x > 0

$4 x^{\log_{8} x} + x^{\log_{8} 4 x} = 4$

$\Leftrightarrow x^{\log_{8} 4 x} + x^{\log_{8} 4 x} = 4$

$\Leftrightarrow x^{\log_{8} 4 x} = 2$

$\Leftrightarrow \log_{8} (x^{\log_{8} 4 x}) = \log_{8} 2$

$\Leftrightarrow \log_{8} x (\frac{2}{3} + \log_{8} x) = \frac{1}{3}$

Đặt $t = \log_{8} x$

Phương trình trở thành:

$t (\frac{2}{3} + t) = \frac{1}{3} \Leftrightarrow t^{2} + \frac{2}{3} t - \frac{1}{3} = 0$ $\Leftrightarrow [\begin{array}{l} t = \frac{1}{3} \\ t = - 1 \end{array}$

Với $t = \frac{1}{3} \Rightarrow \log_{8} x = \frac{1}{3} \Leftrightarrow x = 2$

Với $t = - 1 \Rightarrow \log_{8} x = - 1 \Leftrightarrow x = \frac{1}{8}$

Vậy tập nghiệm của phương trình là: $S = \{2; \frac{1}{8}\}$ .

Câu 51:

Thiết diện qua trục của một hình trụ là một hình vuông có cạnh bằng 2a. Tính theo a thể tích khối trụ đó.

$A . π a^{3};$

$B .2 π a^{2};$

$C .4 π a^{3};$

$D . \frac{2}{3} π a^{3} .$

Xem đáp án

Đáp án đúng là: B

Gọi chiều cao và bán kính đáy của hình trụ lần lượt là h và r.

Thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng 2a nên h = 2a, r = a

Thể tích của khối trụ đó là: V = πr²h = πa².2a = 2πa³

Vậy đáp án đúng là B.

Câu 52:

Trong không gian cho ba điểm phân biệt không thẳng hàng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt?

A. 1;

B. 2;

C. 3;

D. 4

Xem đáp án

Đáp án đúng là: A

Qua 3 điểm phân biệt không thẳng hàng có một và chỉ một mặt phẳng đi qua ba điểm đó

Vậy đáp án đúng là đáp án A

Câu 53:

Vật thể nào dưới đây không phải là khối đa diện?

A. Media VietJack

B. Media VietJack

C. Media VietJack

D. Media VietJack

Xem đáp án

Đáp án đúng là: C

Vật thể cho bởi hình A, B, D là các khối đa diện.

Vật thể cho bởi hình C không phải khối đa diện vì vi phạm điều kiện mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

Câu 54:

Phân tích các đa thức sau thành nhân tử

a) x² + 4xy – 21y²

b) 5x² + 6xy + y²

c) x² + 2xy – 15y²

d) (x – y)² + 4(x – y) – 12

e) x² – 7xy + 10y²

f) x²yz + 5xyz – 14yz

g) x⁴ + 4x² – 5

h) x³ – 19x – 30

i) x³ – 5x² – 14x

j) x³ – 7x – 6

k) x³ – 5x² – 14

Xem đáp án

a) x² + 4xy – 21y²

= x² + 7xy – 3xy – 21y²

= x(x + 7y) – 3y(x + 7y)

= (x + 7y)(x – 3y)

b) 5x² + 6xy + y²

= 5x² + 5xy + xy + y²

= 5x(x + y) + y(x + y)

= (x + y)(5x + y)

c) x² + 2xy – 15y²

= x² + 5xy – 3xy – 15y²

= x(x + 5y) – 3y(x + 5y)

= (x + 5y)(x – 3y)

d) (x – y)² + 4(x – y) – 12

= (x – y)² + 6 (x – y) – 2(x – y) – 12

= (x – y) (x – y + 6) – 2 (x – y + 6)

= (x – y + 6)(x – y – 2)

e) x² – 7xy + 10y²

= x² – 2xy – 5xy + 10y²

= x(x – 2y) – 5y(x – 2y)

= (x – 2y)(x – 5y)

f) x²yz + 5xyz – 14yz

= x²yz + 7xyz – 2xyz – 14yz

= xyz (x + 7) – 2yz(x + 7)

= yz(x + 7)(x – 2)

g) x⁴ + 4x² – 5

= x⁴ – x²+ 5x² – 5

= x²(x² – 1) + 5 (x² – 1)

= (x² – 1) (x² + 5)

= (x – 1)(x + 1)(x² + 5)

h) x³ – 19x – 30

= x³ + 5x² + 6x – 5x²– 25x – 30

= x (x² + 5x + 6) – 5 (x² + 5x + 6)

= (x² + 5x + 6) (x – 5)

= (x – 5)(x² + 2x + 3x + 6)

= (x – 5)[x(x + 2) + 3(x + 2)]

= (x – 5)(x + 2)(x + 3).

i) x³ – 5x² – 14x

= x(x² – 5x – 14)

= x(x² – 7x + 2x – 14)

= x[x(x – 7) + 2 (x – 7)]

= x(x – 7)(x + 2)

j) x³ – 7x – 6

= x³ + 3x²+ 2x – 3x²– 9x – 6

= x(x²+ 3x + 2) – 3(x²+ 3x + 2)

= (x – 3)(x²+ 3x + 2)

= (x – 3)(x² + x + 2x + 2)

= (x – 3)[x(x + 1) + 2(x + 1)]

= (x – 3)(x + 1)(x + 2).

Câu 55:

Liệt kê các số nguyên tố có 2 chữ số nhỏ hơn 25

Xem đáp án

Các số nguyên tố có 2 chữ số nhỏ hơn 25 là: 11; 13; 17; 19; 23.

Câu 56:

Tìm số tiệm cận đứng và ngang của đồ thị hàm số $y = \frac{x + 1}{x^{3} - 3 x - 2}$

A. 2;

B. 3;

C. 1;

D. 0.

Xem đáp án

Đáp án đúng là: C

Hàm số có tập xác định D = ℝ \ {-1; 2}.

Ta có: $y = \frac{x + 1}{x^{3} - 3 x - 2} = \frac{x + 1}{{(x + 1)}^{2} (x - 2)} = \frac{1}{(x + 1) (x - 2)}$

$\Rightarrow \lim_{x \to + \infty} y = \lim_{x \to - \infty} y = 0$ ⇒ Đồ thị hàm số có 1 tiệm cận ngang.

(x + 1)(x – 2) = 0 $\Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 2 \end{array} \Rightarrow$ Đồ thị hàm số có 2 tiệm cận đứng

Vậy đáp án đúng là C.

Câu 57:

Tất cả điều kiện của tham số thực m sao cho đồ thị hàm số $y = \frac{x - 1}{x^{3} + 3 x^{2} + m + 1}$ có đúng 1 tiệm cận đứng là:

A. –5 ≤ m < –1

B. $[\begin{array}{l} m \leq - 5 \\ m > - 1 \end{array}$

C. $[\begin{array}{l} m < - 5 \\ m > - 1 \end{array}$

D. $[\begin{array}{l} m \leq - 4 \\ m > 0 \end{array}$

Xem đáp án

Đáp án đúng là: B

Đồ thị hàm số có đúng 1 tiệm cận đứng khi:

TH1: x³ + 3x² + m + 1 = 0 có đúng 1 nghiệm khác 1

Xét x³ + 3x² + m + 1 = 0 ⇔ x³ + 3x² + 1 = –m, nghiệm khác 1 khi m ≠ –5

Phương trình x³ + 3x² + 1 có đúng 1 nghiệm khi $[\begin{array}{l} - m > 5 \\ - m < 1 \end{array} \Leftrightarrow [\begin{array}{l} m < - 5 \\ m > - 1 \end{array}$

Vậy $[\begin{array}{l} m < - 5 \\ m > - 1 \end{array}$ thì đồ thị hàm số có 1 tiệm cận đứng (1)

TH2: x³ + 3x² + m + 1 = 0 (*) có 2 nghiệm phân biệt trong đó có 1 nghiệm bằng 1.

Thay x = 1 vào (*) được m = –5. Khi đó phương trình (*) trở thành:

x³ + 3x²– 4 = 0 $\Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 2 \end{array}$ thỏa mãn

Vậy m = –5 thỏa mãn (2).

Từ (1) và (2) suy ra m ∈ (–∞; –5] ∪ (–1; +∞)

Câu 58:

Tính tổng: $S = 3^{16} C_{16}^{0} - 3^{15} C_{16}^{1} + 3^{14} C_{16}^{2} - ... + C_{16}^{16}$

A. 3¹⁶;

B. 4¹⁶;

C. 2¹⁶;

D. 5¹⁶.

Xem đáp án

Đáp án đúng là: C

Áp dụng công thức ${(a + b)}^{n} = \sum_{k = 0}^{n} C_{n}^{k} a^{k} b^{n - k}$ và tính chất $C_{n}^{k} = C_{n}^{n - k}$ ta có

$\begin{array}{l} S = 3^{16} C_{16}^{0} - 3^{15} C_{16}^{1} + 3^{14} C_{16}^{2} - ... + C_{16}^{16} \\ S = C_{16}^{0} - 3 C_{16}^{1} + 3^{2} C_{16}^{2} - ... + 3^{16} C_{16}^{16} \\ S = {(1 - 3)}^{16} = 2^{16} \end{array}$

Vậy đáp án đúng là C.

Câu 59:

Chứng minh rằng:

a) a² + b² ≥ 0.

Xem đáp án

a) a²≥ 0, b²≥ 0 nên a² + b² ≥ 0

Câu 60:

b) m² + n² + 2 ≥ 2(m + n).

Xem đáp án

b) m² + n² + 2 ≥ 2(m + n)

m² + n² + 2 – 2m – 2n ≥ 0

(m² – 2m + 1) + (n² – 2n + 1) ≥ 0

(m – 1)² + (m – 1)² ≥ 0 (luôn đúng)

Câu 61:

c) $(a + b) (\frac{1}{a} + \frac{1}{b}) \geq 4$ với a, b > 0.

Xem đáp án

c) Áp dụng BĐT Cô si cho 2 số dương a, b ta có: $(a + b) \geq 2 \sqrt{a b}$ (1)

Áp dụng BĐT Cô si cho 2 số dương $\frac{1}{a}, \frac{1}{b}$ có: $\frac{1}{a} + \frac{1}{b} \geq 2 \sqrt{\frac{1}{a b}}$ (2)

Nhân từng vế của (1) và (2) ta có: $(a + b) (\frac{1}{a} + \frac{1}{b}) \geq 2 \sqrt{a b} .2 \sqrt{\frac{1}{a b}} = 4$ (đpcm)

Câu 62:

Khi phương trình bậc hai ax² + bx + x = 0 có biệt thức D = b² – 4ac < 0 thì có bao nhiêu nghiệm?

Xem đáp án

Khi phương trình bậc hai ax² + bx + x = 0 có biệt thức D = b² – 4ac < 0 thì phương trình vô nghiệm.

Câu 63:

Trong mặt phẳng tọa độ Oxy cho đường thẳng d: x – 2y + 3 = 0 và I(1; –2). Viết phương trình đường thẳng d' sao cho d’ là ảnh của đường thẳng d qua phép đối xứng tâm I.

Xem đáp án

Lấy M(–3; 0) thuộc d, khi đó M’ = Đ_I(M) là điểm thuộc d’.

Ta có M’ = Đ_I(M) nên I(1; –2) là trung điểm của MM’

\Rightarrow \{\begin{cases} x_{M^{'}} = 2.1 - (- 3) = 5 \\ y_{M^{'}} = 2. (- 2) - 0 = - 4 \end{cases} \Rightarrow M^{'} (5; - 4)

d’ là ảnh của d qua phép đối xứng tâm I nên d’ // d và d’ đi qua M’(5; –4)

⇒ (d’): x – 2y – 13 = 0.

Câu 64:

Cho a, b, c là những số nguyên thỏa mãn: ${(\frac{1}{a} + \frac{1}{b} + \frac{1}{c})}^{2} = \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}$

Chứng minh: a³ + b³ + c³ chia hết cho 3.

Xem đáp án

${(\frac{1}{a} + \frac{1}{b} + \frac{1}{c})}^{2} = \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}$

$\Leftrightarrow {[(\frac{1}{a} + \frac{1}{b}) + \frac{1}{c}]}^{2} = \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}$

Phân tích vế trái ta được:

$\begin{array}{l} {((\frac{1}{a} + \frac{1}{b}) + \frac{1}{c})}^{2} = {(\frac{1}{a} + \frac{1}{b})}^{2} + \frac{2}{a c} + \frac{2}{b c} + {(\frac{1}{c})}^{2} = \frac{1}{a^{2}} + \frac{2}{a b} + \frac{1}{b^{2}} + \frac{2}{a c} + \frac{2}{b c} + \frac{1}{c^{2}} \\ \Rightarrow \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} + \frac{2}{a b} + \frac{2}{a c} + \frac{2}{b c} = \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \\ \Rightarrow 2. (\frac{1}{a b} + \frac{1}{a c} + \frac{1}{b c}) = 0 \\ \Rightarrow \frac{c}{a b c} + \frac{b}{a b c} + \frac{a}{a b c} = 0 \\ \Rightarrow a + b + c = 0. a b c = 0 \\ \Rightarrow a + b = - c \\ \Rightarrow - (a + b) = c \end{array}$

Thay vào ta có: a³ + b³ + c³ = a³ + b³ – (a + b)³ = –3a²b – 3ab² = 3 (–a²b – ab²) ⋮ 3

Câu 65:

Cho hàm số f(x) liên tục trên ℝ thỏa mãn f(3x) = f(x) – 2x, ∀x ∈ ℝ và

\int_{0}^{1} f (x) d x = 5

. Tính I =

\int_{0}^{3} f (x) d x

.

A. I = 7;

B. I = 12;

C. I = 4;

D. I = 10;

Xem đáp án

Đáp án đúng là: A

Từ giả thiết ta có: $\int_{0}^{1} f (3 x) d x = \int_{0}^{1} |f (x) - 2 x| d x = \int_{0}^{1} f (x) d x - \int_{0}^{1} 2 x d x = 5 - x^{2} |\begin{array}{l} 1 \\ 0 \end{array} = 4$

Đặt u = 3x ⇒ du = 3dx ⇒ dx = $\frac{d u}{3}$

Đổi cận: $\{\begin{cases} x = 0 \Rightarrow u = 0 \\ x = 1 \Rightarrow u = 3 \end{cases}$

Khi đó: $\int_{0}^{1} f (3 x) d x = \int_{0}^{3} f (u) \frac{d u}{3} = 4 \Leftrightarrow I = \int_{0}^{3} f (x) d x = 12$

Vậy đáp án B là đáp án đúng.

Câu 66:

Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình.

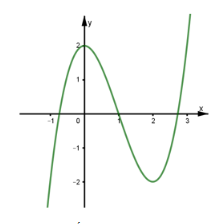
Media VietJack

Gọi m là số nghiệm của phương trình f(f(x)) = 1. Khẳng định nào sau đây là đúng?

A. m = 6;

B. m = 7;

C. m = 5;

D. m = 9.

Xem đáp án

Đáp án đúng là: B

Đặt f(x) = u khi đó nghiệm của phương trình f(f(x)) = 1 chính là hoành độ giao điểm của đồ thị f(u) với đường thẳng y = 1.

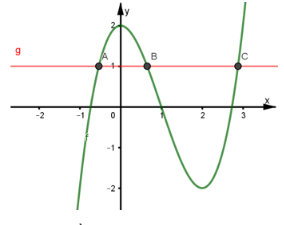
Dựa vào đồ thị ta có ba nghiệm:

$[\begin{array}{l} f (x) = u_{1} \\ f (x) = u_{2} \\ f (x) = u_{3} \end{array}$

Với u₁ ∈ (-1; 0), u₂ ∈ (0; 1), u₃ ∈ ( $\frac{5}{2}$ ; 3)

Tiếp tục xét số giao điểm của đồ thị hàm số f(x) với từng đường thẳng y = u₁, y = u₂, y = u₃.

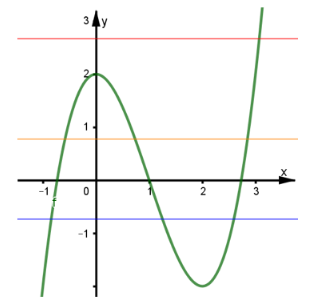
Dựa vào đồ thị ta có được 7 giao điểm.

Suy ra phương trình ban đầu f(f(x)) = 1 có 7 nghiệm

Câu 67:

Cho hình lăng trụ ABC.A'B'C' có thể tích là V. Gọi M là điểm thuộc cạnh CC' sao cho CM = 3C'M. Tính thể tích khối chóp M.ABC

$A . \frac{V}{4};$

$B . \frac{3 V}{4};$

$C . \frac{V}{12};$

$D . \frac{V}{6} .$

Xem đáp án

Đáp án đúng là: A

Do CM = 3C'M ⇒ d(M; (ABC)) = $\frac{3}{4}$ d(C'(ABC))

Ta có: V_M.ABC = $\frac{3}{4}$ , V_C'.ABC = $\frac{3}{4} \cdot \frac{V}{3} = \frac{V}{4}$

Vậy đáp án đúng là A.

Câu 68:

Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AC = 2a, SA vuông góc với mặt phẳng (ABCD), SC tạo với mặt phẳng (SAB) một góc 30o. Gọi M là một điểm trên cạnh AB sao cho BM = 3MA. Khoảng cách từ điểm A đến mặt phẳng (SCM) là:

A. $\frac{\sqrt{34} a}{51}$

B. $\frac{2 \sqrt{34} a}{51}$

C. $\frac{3 \sqrt{34} a}{51}$

D. $\frac{4 \sqrt{34} a}{51}$

Xem đáp án

Đáp án đúng là: B

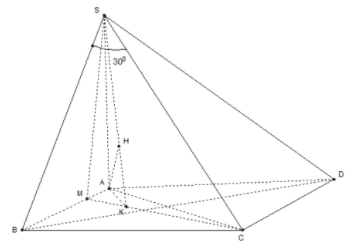
Đặc điểm của hình: SC tạo với mặt phẳng (SAB) góc $\hat{C S B} = 30 °$ .

BC = $\sqrt{3} a$ ; SB = BC.tan 30^o = a; MC = $\sqrt{{(\frac{3 a}{4})}^{2} + 3 a^{2}} = \frac{\sqrt{57}}{4} a$

MA = $\frac{a}{4}$ ; AC = 2a; AS = $2 \sqrt{2} a$ ; AK = $\frac{2 S_{A M C}}{M C} = \frac{\sqrt{19}}{9} a$

Xác định khoảng cách: d(A, (SBC)) = AH

$\frac{1}{A H^{2}} = \frac{1}{A K^{2}} + \frac{1}{A S^{2}} = \frac{1}{{(\frac{\sqrt{19}}{9} a)}^{2}} + \frac{1}{{(2 \sqrt{2} a)}^{2}} = \frac{153}{8 a^{2}}$

Vậy d(A, (SBC)) = AH = $\frac{2 \sqrt{34}}{51}$

Vậy đáp án B là đáp án đúng.

Câu 69:

Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Kẻ 2 tiếp tuyến AM, AN và cát tuyến ABC với đường tròn (AB < AC). Qua O kẻ OK vuông góc với BC tại K, OK cắt MN tại S. Chứng minh SC là tiếp tuyến của đường tròn (O).

Xem đáp án

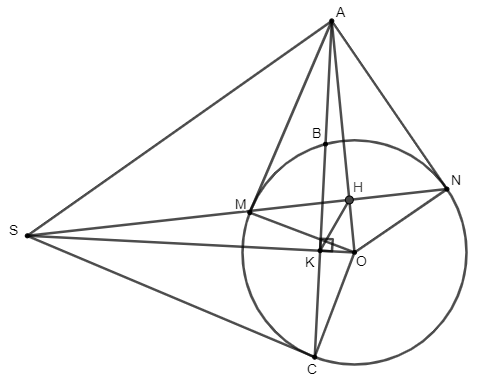
Gọi AO ∩ MN ≡ H

Theo tính chất hai tiếp tuyến cắt nhau: AM = AN

Mà OM = ON nên OA là trung trực của MN

Do đó OA ⊥ MN $\Leftrightarrow \hat{S H A} = 90 °$ (1)

Mặt khác BC ⊥ OK ⟹ AC⊥ OS ⟹ $\hat{S K A} = 90 °$ (2)

Từ (1) và (2) suy ra tứ giác SKHA nội tiếp (hai góc cùng nhìn một cạnh bằng nhau)

Do đó theo tính chất tứ giác nội tiếp thì: OK.OS = OH.OA (*)

Vì AM là tiếp tuyến của đường tròn (O) nên AM ⊥ OM

Xét tam giác vuông AMO có đường cao MH, theo hệ thức lượng trong tam giác vuông thì: OC² = R² = OM² = OH.OA (**)

Từ (*) và (**) ⟹ OC² = OK.OS $\Leftrightarrow \frac{O C}{O K} = \frac{O S}{O C}$

Do đó tam giác OCK đồng dạng với tam giác OSC (cạnh – góc – cạnh)

\Rightarrow \hat{O C S} = \hat{O K C} = 90 °

⇒ SC ⊥ OC ⇒ SC là tiếp tuyến của đường tròn (O).

Câu 70:

Tập nghiệm của phương trình 2sin2x + 1 = 0 là:

A. $S = \{- \frac{π}{6} + k π, \frac{7 π}{12} + k π, k \in ℤ\}$

B. $S = \{- \frac{π}{12} + k π, \frac{7 π}{12} + k π, k \in ℤ\}$

C. $S = \{- \frac{π}{6} + k π, \frac{7 π}{12} + k 2 π, k \in ℤ\}$

D. $S = \{- \frac{π}{12} + k 2 π, \frac{7 π}{12} + k 2 π, k \in ℤ\}$

Xem đáp án

Đáp án đúng là: B

Ta có: 2sin2x + 1 = 0

$\Leftrightarrow \sin 2 x = - \frac{1}{2} \Leftrightarrow [\begin{array}{l} 2 x = - \frac{π}{6} + k 2 π \\ 2 x = \frac{7 π}{6} + k 2 π \end{array} \Leftrightarrow [\begin{array}{l} x = - \frac{π}{12} + k π \\ x = \frac{7 π}{12} + k π \end{array} (k \in ℤ)$

Vậy tập nghiệm của phương trình là $S = \{- \frac{π}{12} + k π, \frac{7 π}{12} + k π, k \in ℤ\}$

Vậy đáp án đúng là B.

Câu 71:

Tìm phần thực, phần ảo của số phức $z = \frac{3 - i}{1 + i} + \frac{2 + i}{i}$

A. Phần thực: a = 2, phần ảo: b = -4i;

B. Phần thực: a = 2, phần ảo: b = -4;

C. Phần thực: a = 2, phần ảo: b = 4i;

D. Phần thực: a = 2, phần ảo: b = 4.

Xem đáp án

Đáp án đúng là: B

$\begin{array}{l} z = \frac{3 - i}{1 + i} + \frac{2 + i}{i} = \frac{(3 - i) (1 - i)}{1^{2} - i^{2}} + \frac{(2 + i) i}{i^{2}} = \frac{i^{2} - 4 i + 3}{1 + 1} + \frac{- 1 + 2 i}{- 1} \\ = \frac{- 1 - 4 i + 3}{2} - (- 1 + 2 i) = 2 - 4 i \end{array}$

Vậy phần thực: a = 2, phần ảo: b = –4

Đáp án đúng là B.

Câu 72:

Tính chu vi hình thang biết đáy lớn bằng 14cm, đáy bé bằng 10cm, 2 cạnh bên lần lượt bằng 6cm, và 8cm.

A. 36 cm;

B. 38 cm;

C. 32 cm;

D. 34 cm.

Xem đáp án

Áp dụng theo công thức tính chu vi hình thang ta có

P = a + b + c + d

= 14 + 10 + 6 + 8

= 38cm

Đáp số: 38cm

Chọn B

Câu 73:

Xét số phức z thỏa mãn $\frac{z + 2}{z - 2 i}$ là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số phức z luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng:

A. 1

B. $\sqrt{2}$

C. $2 \sqrt{2}$

D. 2

Xem đáp án

Đáp án đúng là: B

Gọi z = a + bi ta có:

$\begin{array}{l} \frac{z + 2}{z - 2 i} = \frac{(a + 2) + b i}{a + (b - 2 i) i} = \frac{|(a + 2) + b i| |a - (b - 2) i|}{|a + (b - 2) i| |a - (b - 2) i|} \\ = \frac{(a + 2) a - (a + 2) (b - 2) i + a b i + b (b - 2)}{a^{2} + {(b - 2)}^{2}} \\ = \frac{a^{2} + 2 a + b^{2} - 2 b}{a^{2} + {(b - 2)}^{2}} - \frac{(a + 2) (b - 2) - a b}{a^{2} + {(b - 2)}^{2}} i \end{array}$

Để số trên là số thuần ảo thì phải có phần thực bằng 0 ⇒ a² + 2a + b² – 2b = 0

Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm I(-1;1) bán kính: $R = \sqrt{{(- 1)}^{2} + 1^{2} - 0} = \sqrt{2}$

Vậy đáp án B là đáp án đúng

Câu 74:

Giải phương trình sau (12x + 7)²(3x + 2) (2x + 1) = 3

Xem đáp án

(12x + 7)²(3x + 2) (2x + 1) = 3

⇔ (12x + 7)² . 4 . (3x + 2) . 6 . (2x + 1) = 3.4.6

⇔ (12x + 7)²(12x + 8) (12x + 6) = 72

Đặt 12x + 7 = t.

Ta có phương trình ẩn t:

t² (t + 1)(t – 1) = 72

⇔ t² (t² – 1) = 72

⇔ t⁴ – t² – 72 = 0

⇔ t⁴ – 9t² + 8t² – 72 = 0

⇔ t²(t²– 9) + 8(t²– 9) = 0

⇔ (t²– 9)(t²+ 8) = 0

mà t²+ 8 > 0 với mọi t ⇒ t² – 9 = 0 ⇔ (t - 3)(t + 3) = 0

$\Leftrightarrow \{\begin{cases} t = 3 \\ t = - 3 \end{cases} \Leftrightarrow \{\begin{cases} 12 x + 7 = 3 \\ 12 x + 7 = - 3 \end{cases} \Leftrightarrow \{\begin{cases} x = - \frac{1}{3} \\ x = - \frac{5}{6} \end{cases}$

Vậy phương trình đã cho có tập nghiệm là S = $\{- \frac{1}{3}; - \frac{5}{6}\}$ .

Câu 75:

Tìm GTNN của $P = 3 x^{2} + \frac{1}{x}$ với x > 0.

Xem đáp án

$\begin{array}{l} P = 3 x^{2} + \frac{1}{x} = 3 x^{2} + \frac{1}{2 x} + \frac{1}{2 x} \\ P \geq 3. \sqrt[3]{\frac{3 x^{2} .1}{2 x .2 x}} = 3. \sqrt[3]{\frac{3}{4}} \end{array}$

Khi $3 x^{2} = \frac{1}{2 x} \Rightarrow x = \sqrt[3]{\frac{1}{6}}$

Câu 76:

Thực hiện phép tính:

a) 483 + (-56) + 263 + (-64)

Xem đáp án

a) 483 + (-56) + 263 + (-64)

= 483 + 263 + (-56) + (-64)

= 746 + (-120)

= 626

Câu 77:

b) 371 + (-531) + (-271) + 731

Xem đáp án

b) 371 + (-531) + (-271) + 731

= 371+ (-271) + (-531) + 731

= 100 + 200

= 300

Câu 78:

c) 3251 – 243 - 3250

Xem đáp án

c) 3251 – 243 – 3250

= 3251 – 3250 – 243

= 1 – 243

= -242

Câu 79:

d) 279 – (145 + 279)

Xem đáp án

d) 279 – (145 + 279)

= 279 – 279 – 145

= 0 – 145 = -145

Câu 80:

Tính hợp lí:

a) 942 – 2567 + 2563 – 1942

Xem đáp án

a) 942 – 2567 + 2563 – 1942

= (942 – 1942) + (2563 – 2567)

= (-1000) + (-4)

= -1004

Câu 81:

b) 42.53 + 47.156 – 47.114

Xem đáp án

b) 42.53 + 47.156 – 47.114

= 42.53 + 47.(156 – 114)

= 42.53 + 47.42

= 42.(53 + 47)

= 42.100

= 4200

Câu 82:

Cho a, b, c > 0. Chứng minh rằng: $\frac{a^{3}}{b} + \frac{b^{3}}{c} + \frac{c^{3}}{a} \geq a b + b c + c a$

Xem đáp án

Áp dụng BĐT Cô si với 3 số không âm ta có:

$\frac{a^{3}}{b} + \frac{a^{3}}{b} + a^{2} \geq \frac{3 \sqrt[3]{a^{3} . a^{3} . b^{2}}}{b^{2}} = 3 a^{2}$

$\begin{array}{l} \frac{b^{3}}{c} + \frac{b^{3}}{c} + b^{2} \geq 3 b^{2} \\ \frac{c^{3}}{a} + \frac{c^{3}}{a} + c^{2} \geq 3 c^{2} \\ \Rightarrow 2 (\frac{a^{3}}{b} + \frac{b^{3}}{c} + \frac{c^{3}}{a}) + a^{2} + b^{2} + c^{2} \geq 3 (a^{2} + b^{2} + c^{2}) \\ \Rightarrow \frac{a^{3}}{b} + \frac{b^{3}}{c} + \frac{c^{3}}{a} \geq a^{2} + b^{2} + c^{2} \end{array}$

Mà a² + b² + c² ≥ ab + bc + ca

$\Rightarrow \frac{a^{3}}{b} + \frac{b^{3}}{c} + \frac{c^{3}}{a} \geq a b + b c + c a$

Câu 83:

Cho tam giác MNP vuông tại M, đường cao MH. Biết NH = 5 cm, HP = 9 cm. Độ dài MH bằng:

A. 4 cm;

B. 7 cm;

C. $3 \sqrt{5}$ cm;

D. 4,5 cm.

Xem đáp án

Đáp án đúng là: C

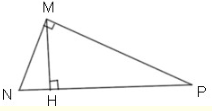
Áp dụng hệ thức lượng trong tam giác vuông MNP ta có:

MH² = NH.HP = 5.9 = 45

$\Rightarrow M H = \sqrt{45} = 3 \sqrt{5}$ cm

Vậy đáp án đúng là C.

Câu 84:

Cho tứ diện ABCD. Gọi M là trung điểm cạnh AB, N thuộc cạnh AC sao cho AN=2NC, P thuộc cạnh BD sao cho BP = 3PD.

a) Xác định giao tuyến của hai mặt phẳng (MNP) và (BCD).

Xem đáp án

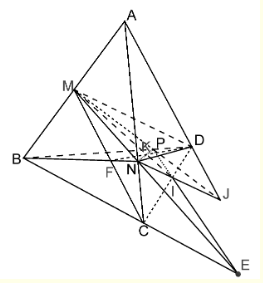
a) Từ giả thiết có P là điểm chung thứ nhất của hai mặt phẳng (MNP) và (BCD).

Vì MN không song song với BC nên gọi E = MN ∩ BC, thì M là điểm chung thứ hai của hai mặt phẳng (MNP) và (BCD).

Vậy PE = (MNP) ∩ (BCD)

Câu 85:

b) Xác định giao điểm I của đường thẳng CD và mặt phẳng (MNP); giao điểm J của đường thẳng AD và mặt phẳng (MNP). Từ đó suy ra ba điểm N, I, J thẳng hàng.

Xem đáp án

b) Giả sử PE ∩ CD = I thì I là điểm chung của CD và mặt phẳng (MNP)

Suy ra CD ∩ (MNP) = I

Trong mặt phẳng (ABD), kéo dài MP và AD cắt nhau tại J, suy ra AD ∩ (MNP) = J

Từ đó ta thấy N, I, J đều thuộc hai mặt phẳng (MNP) và (ACD) nên N, I, J thuộc giao tuyến của hai mặt phẳng (MNP) và (ACD). Vậy 3 điểm N, I, J thẳng hàng.

Câu 86:

c) Giả sử điểm P di động trên cạnh BD. Gọi K là giao điểm của MI và NP. Chứng minh K thuộc một đường thẳng cố định.

Xem đáp án

c) Trong mặt phẳng (ABC) gọi F = MC ∩ NB

Xét hai mặt phẳng (NBD) và (MCD) có hai điểm chung là điểm D và điểm F.

Suy ra, (NBD) ∩ (MCD) = DF

Vì M, N cố định nên F cố định, do đó đường thẳng DF cố định.

Hơn nữa K = MI ∩ NP nên K thuộc cả hai mặt phẳng (NBD) và (MCD)

Suy ra K thuộc đường thẳng DF cố định.

Câu 87:

Cho tứ diện ABCD có I, J lần lượt là trung điểm AC, BC. Gọi K thuộc BD sao cho KD < KB. Gọi E là giao điểm của JK và CD, F là giao điểm của AD và IE. Giao tuyến của (IJK) và (ACD) là:

A. đường thẳng AI;

B. đường thẳng IF;

C. đường thẳng JE;

D. đường thẳng IE.

Xem đáp án

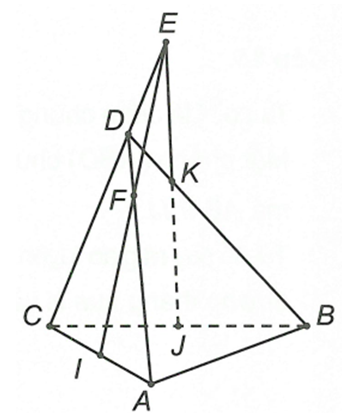
Gọi E là giao điểm của JK và CD

$\Rightarrow \{\begin{cases} E \in I J \subset (I J K) \\ E \in C D \subset (A C D) \end{cases} \Rightarrow$ E là điểm chung thứ nhất

Lại có: $\{\begin{cases} I \in I E \subset (I J K) \\ I \in A C \subset (A C D) \end{cases} \Rightarrow$ I là điểm chung thứ hai

Vậy (ACD) ∩ (IJK) = IE

Vậy đáp án đúng là D.

Câu 88:

Cho đoạn thẳng AB và M là một điểm nằm trên đoạn AB sao cho AM = $\frac{1}{5}$ AB. Giá trị của k để có đẳng thức $\vec{A M} = k . \vec{A B}$ là:

A. k = $- \frac{1}{5}$ ;

B. $\frac{1}{5}$ ;

C. 5;

D. -5.

Xem đáp án

Đáp án đúng là: B

Ta có: AM = $\frac{1}{5}$ AB $\Rightarrow \frac{A M}{A B} = \frac{1}{5}$

Theo đề bài ta có: $\vec{A M} = k . \vec{A B} \Rightarrow |\vec{A M}| = |k| . |\vec{A B}| \Rightarrow |k| = \frac{|\vec{A M}|}{|\vec{A B}|} = \frac{1}{5}$

Mà $\vec{A M}$ và $\vec{A B}$ cùng hướng nên k = $\frac{1}{5}$

Vậy đáp án đúng là B.

Câu 89:

Chứng minh rằng: x² + y² +z² ≥ xy + yz + xz với mọi x, y, z.

Xem đáp án

x² + y² + z² ≥ xy + yz + xz (1)

⇔ 2x² + 2y² + 2z² ≥ 2xy + 2yz + 2xz

⇔ 2x² + 2y² + 2z² – 2xy – 2yz – 2xz ≥ 0

⇔ (x²– 2xy + y²) + (y²– 2yz + z²) + (z²– 2xz + x²) ≥ 0

⇔ (x – y)² + (y – z)² + (z – x)² ≥ 0 (đpcm)

Dấu “ = ” xảy ra khi x = y = z

Câu 90:

Cho x² + y² +z² = xy + yz + xz. Chứng minh z = x = y.

Xem đáp án

x² + y² +z² = xy + yz + xz

⇔ x² + y² +z² – xy – yz – xz = 0

⇔ 2x² + 2y² + 2z² – 2xy – 2yz – 2xz = 0

⇔ (x²– 2xy + y²) + (y²– 2yz + z²) + (z²– 2xz + x²) = 0

⇔ (x – y)² + (y – z)² + (z – x)² = 0

⇔ $[\begin{array}{l} x - y = 0 \\ y - z = 0 \\ z - x = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = y \\ y = z \\ z = x \end{array} \Leftrightarrow x = y = z$ (đpcm)

Câu 91:

Hình nón có thiết diện qua trục là tam giác đều và có thể tích $V = \frac{\sqrt{3}}{3} π a^{3}$ . Diện tích xung quanh S của hình nón đó là:

A. $S = \frac{1}{2} π a^{2}$

B. $S = 4 π a^{2}$

C. $S = 2 π a^{2}$

D. $S = π a^{2}$

Xem đáp án

Đáp án đúng là: C

Vì thiết diện là tam giác đều nên l = 2r và h = r $\sqrt{3}$

Ta có: $V = \frac{\sqrt{3}}{3} π a^{3} \Leftrightarrow \frac{1}{3} π r^{2} h = \frac{\sqrt{3}}{3} π a^{3} \Leftrightarrow r = a \Rightarrow l = 2 a$

$S = π r l = 2 π a^{2}$

Câu 92:

Tìm m nguyên để hệ phương trình sau có nghiệm duy nhất là nghiệm nguyên.

a) $\{\begin{cases} m x + 2 y = m + 1 \\ 2 x + m y = 2 m - 1 \end{cases}$

Xem đáp án

a) Từ phương trình thứ nhất suy ra 2y = m + 1 – mx $\Rightarrow y = \frac{m + 1 - m x}{2}$

Thay vào phương trình thứ hai ta được:

$2 x + m \cdot \frac{m + 1 - m x}{2} = 2 m - 1$

⇔ 4x + m² + m – m²x = 4m – 2

⇔ x(m²– 4) = m²– 3m + 2

⇔ x(m – 2)(m + 2) = (m – 2)(m – 1) (*)

Nếu m = 2 thì (*) ⇔ 0x = 0, phương trình này vô số nghiệm.

Nếu m = -2 thì (*) ⇔ 0x = 12, phương trình này vô nghiệm

Nếu m ≠ 2 và m ≠ -2 thì (*) ⇔ $x = \frac{m - 1}{m + 2} \Rightarrow y = \frac{m + 1 - m x}{2} = \frac{2 m + 1}{m + 2}$

Như vậy trong trường hợp này hệ có nghiệm duy nhất:

$\begin{array}{l} x = \frac{m - 1}{m + 2} = 1 - \frac{3}{m + 2} \\ y = \frac{2 m + 1}{m + 2} = 2 - \frac{3}{m + 2} \end{array}$

Ta cần tìm m ∈ ℤ sao cho x, y ∈ ℤ.

$\Rightarrow \frac{3}{m + 2} \in ℤ$ ⇔ m + 2 ∈ {-1, 1, 3, -3} ⇔ m ∈ {-3, -1, 1, -5}

Các giá trị này thỏa mãn m ≠ 2 và m ≠ -2.

Vậy m ∈ {-3, -1, 1, -5}

Câu 93:

b) $\{\begin{cases} (m + 1) x - 2 y = m - 1 \\ m^{2} x - y = m^{2} + 2 m \end{cases}$

Xem đáp án

b) $\{\begin{cases} (m + 1) x - 2 y = m - 1 \\ m^{2} x - y = m^{2} + 2 m \end{cases} \Leftrightarrow \{\begin{cases} (m + 1) x - 2 y = m - 1 (1) \\ 2 m^{2} x - 2 y = 2 m^{2} + 4 m (2) \end{cases}$

Từ (1) và (2) ⇒ (2m² – m – 1)x = 2m² + 3m + 1

$\begin{array}{l} \Rightarrow x = \frac{2 m^{2} + 3 m + 1}{2 m^{2} - m - 1} = \frac{2 m^{2} - m - 1}{2 m^{2} - m - 1} + \frac{4 m + 2}{2 m^{2} - m - 1} \\ = 1 + \frac{4 m + 2}{2 m^{2} - m - 1} = 1 + \frac{2 m + 1}{(m - 1) (m + \frac{1}{2})} (3) \end{array}$

Từ (3) ta thấy điều kiện để hệ đã cho có nghiệm là m ≠ 1

Và điều kiện để hệ có nghiệm duy nhất là m ≠ 1 và m ≠ $- \frac{1}{2}$

Với các điều kiện đó từ (3) ⇒ $x = 1 + \frac{2}{m - 1}$ (*)

Thay (*) vào (1) ta được: $m + 1 + \frac{2 (m + 1)}{m - 1} - 2 y = m - 1 \Rightarrow y = 1 + \frac{m + 1}{m - 1} = 2 + \frac{2}{m - 1}$ (**)

Từ (*) và (**) suy ra x, y là nghiệm nguyên duy nhất ⇔ m – 1 là ước của 2

⇒ m – 1 ∈ {-2, -1, 1, 2} ⇒ m ∈ {-1, 0, 2, 3}.

Các giá trị này thỏa mãn m ≠ 1 và m ≠ $- \frac{1}{2}$

Vậy m ∈ {-1, 0, 2, 3}.

Câu 94:

Tìm tập xác định của hàm số y = (7^x)²+ x – 2.

Xem đáp án

Tập xác định của hàm số y = (7^x)²+ x – 2 là ℝ

Câu 95:

Trong không gian với hệ tọa độ Oxyz, tìm bán kính R của đường tròn giao tuyến của mặt phẳng 2x – 2y – z + 9 = 0 và mặt cầu x² + y² + z² – 6x + 4y – 2z – 86 = 0.

A. R = 9;

B. R = 4;

C. R = 2;

D. R = 8.

Xem đáp án

Đáp án đúng là: D

Mặt cầu có tâm O (3; -2; 1), bán kính R = 10

Khoảng cách từ tâm đến mặt phẳng là: $d = \frac{|2.3 - 2. (- 2) - 1 + 9|}{\sqrt{2^{2} + {(- 2)}^{2} + {(- 1)}^{2}}} = 6$

Vậy bán kính đường tròn giao tuyến là: $r = \sqrt{R^{2} - d^{2}} = \sqrt{10^{2} - 6^{2}} = 8$

Đáp án đúng là đáp án D.

Câu 96:

Tính bán kính đường tròn giao tuyến của mặt cầu S(O;r) và mặt phẳng (α) biết rằng khoảng cách từ tâm O đến (α) bằng $\frac{r}{3}$

A. $\frac{2 r}{3}$

B. $\frac{\sqrt{6} r}{3}$

C. $\frac{8 r}{9}$

$\frac{2 \sqrt{2} r}{3}$

Xem đáp án

Đáp án đúng là: D

Gọi khoảng cách từ O đến (α) là d, bán kính đường tròn giao tuyến là R

Áp dụng định lí Pytago ta có: $R^{2} + d^{2} = r^{2} \Rightarrow R = \sqrt{r^{2} - d^{2}} = \sqrt{r^{2} - {(\frac{r}{3})}^{2}} = \frac{2 \sqrt{2} r}{3}$

Vậy đáp án đúng là D.

Câu 97:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = 2a, AD = DC = a, SA = a $\sqrt{2}$ , SA ⊥ (ABCD). Tính cosin của góc giữa hai mặt phẳng (SBC) và (SCD).

A. $\frac{\sqrt{5}}{3}$

B. $\frac{\sqrt{7}}{3}$

C. $\frac{\sqrt{3}}{3}$

D. $\frac{\sqrt{6}}{3}$

Xem đáp án

Đáp án đúng là: D

Vì AB // CD ⇒ AB // (SDC) ⇒ d(B; (SDC)) = d(A; (SDC)) = AK = $\frac{\sqrt{6} a}{3}$ .

Dễ thấy $\{\begin{cases} B C ⊥ A C \\ B C ⊥ S A \end{cases} \Rightarrow B C ⊥ S C$ ⇒ d(B; SC) = BC = $\sqrt{2} a$

Vậy $\sin α = \frac{d (B; (S C D))}{d (B; S C)} = \frac{\sqrt{3}}{3} \Rightarrow \cos α = \sqrt{1 - \frac{1}{3}} = \sqrt{\frac{2}{3}} = \frac{\sqrt{6}}{3}$

Đáp án đúng là D.

Câu 98:

Tính $P = \frac{\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{2012}}{\frac{2011}{1} + \frac{2010}{2} + \frac{2009}{3} + ... + \frac{1}{2011}}$

Xem đáp án

$\begin{array}{l} P = \frac{\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{2012}}{\frac{2011}{1} + \frac{2010}{2} + \frac{2009}{3} + ... + \frac{1}{2011}} \\ P = \frac{\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{2012}}{1 + (1 + \frac{2010}{2}) + (1 + \frac{2009}{3}) + ... + (1 + \frac{1}{2011})} \\ P = \frac{\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{2012}}{\frac{2012}{2012} + \frac{2012}{2} + \frac{2012}{3} + ... + \frac{2012}{2011}} \\ P = \frac{\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{2012}}{2012 (\frac{1}{2} + \frac{1}{3} + ... + \frac{1}{2011} + \frac{1}{2012})} \\ P = \frac{1}{2012} \end{array}$

Câu 99:

Tìm tập xác định của hàm số

y = \frac{3^{x + 2}}{x - 1}

Xem đáp án

$y = \frac{3^{x + 2}}{x - 1}$ có nghĩa khi x – 1 ≠ 0 ⇔ x ≠ 1

Vậy tập xác định của hàm số: $y = \frac{3^{x + 2}}{x - 1}$ là D = ℝ \ {1}.

Câu 100:

Tìm tập xác định của hàm số

y = \frac{3^{x + 2}}{x - 1}

Xem đáp án

$y = \frac{3^{x + 2}}{x - 1}$ có nghĩa khi x – 1 ≠ 0 ⇔ x ≠ 1

Vậy tập xác định của hàm số: $y = \frac{3^{x + 2}}{x - 1}$ là D = ℝ \ {1}.

Câu 101:

Tập xác định của hàm số $y = \frac{x + 2}{x - 1}$ là:

A. ℝ \ {1};

B. ℝ \ {2};

C. ℝ \ {-1};

D. ℝ \ {-2}.

Xem đáp án

Đáp án đúng là: A

$y = \frac{x + 2}{x - 1}$ có nghĩa khi x – 1 ≠ 0 ⇔ x ≠ 1

Vậy tập xác định của hàm số: $y = \frac{x + 2}{x - 1}$ là D = ℝ \ {1}.

Vậy đáp án đúng là A

Câu 102:

Tìm giá trị nhỏ nhất m của hàm số: $y = x^{2} + \frac{2}{x}$ trên đoạn $[\frac{1}{2}; 2]$

A. m = 3;

B. m = 5;

C. m = $\frac{17}{4}$ ;

D. m = 4.

Xem đáp án

Đáp án đúng là: A

Hàm số xác định trên đoạn $[\frac{1}{2}; 2]$ , $y' = 2 x - \frac{2}{x^{2}} = 0 \Leftrightarrow x = 1 \in [\frac{1}{2}; 2]$

$y (\frac{1}{2}) = \frac{17}{4}; y (1) = 3; y (2) = 5$

Giá trị nhỏ nhất của hàm số $y = x^{2} + \frac{2}{x}$ trên đoạn $[\frac{1}{2}; 2]$ là m = 3.

Vậy đáp án đúng là A.

Câu 103:

Phân tích đa thức sau thành nhân tử x² –xy + x – y

Xem đáp án

Cách 1: Nhóm hai hạng tử thứ 1 và thứ 2, hạng tử thứ 3 và thứ 4

x² – xy + x – y

= (x² – xy) + (x – y)

(Nhóm thứ nhất có nhân tử chung là x)

= x(x – y) + (x – y)

(Xuất hiện nhân tử chung x – y)

= (x + 1)(x – y)

Cách 2: Nhóm hạng tử thứ 1 và thứ 3 ; hạng tử thứ 2 và thứ 4

x² – xy + x – y

= (x²+ x) – (xy + y)

(nhóm thứ nhất có nhân tử chung là x ; nhóm thứ hai có nhân tử chung là y)

= x.(x + 1) – y.(x + 1)

(Xuất hiện nhân tử chung x + 1)

= (x – y)(x + 1)

Câu 104:

Đội thanh niên xung kích có của một trường phổ thông có 12 học sinh, gồm 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá 2 trong ba lớp trên. Hỏi có bao nhiêu cách chọn như vậy?

A. 225;

B. 495;

C. 372;

D. 219.

Xem đáp án

Đáp án đúng là: A

TH1: 4 học sinh được chọn thuộc một lớp:

Thuộc lớp A: Có $C_{5}^{4}$ cách chọn

Thuộc lớp B: Có $C_{4}^{4}$ cách chọn

Trong trường hợp này có: $C_{5}^{4} + C_{4}^{4}$ = 6 cách chọn.

TH2: 4 học sinh thuộc hai lớp:

Thuộc lớp A và B: có $C_{9}^{4} - (C_{5}^{4} + C_{4}^{4}) = 120$ cách chọn

Thuộc lớp B và C: có $C_{7}^{4} - C_{4}^{4} = 34$ cách chọn
Thuộc lớp A và C: có $C_{8}^{4} - C_{5}^{4} = 65$ cách chọn

Trong trường hợp này có: 120 + 34 + 65 = 219 cách chọn

Vậy có 219 + 6 = 225 cách chọn đội thanh niên xung kích thỏa mãn yêu cầu đầu bài.

Vậy đáp án đúng là A.

Câu 105:

Giải phương trình (x²− 1)(x²+ 4x + 3) = 192

Xem đáp án

Biến đổi phương trình thành:

(x²– 1)(x + 1)(x + 3) = 192 ⇔ (x – 1)(x + 1)² (x + 3) = 192

Đặt x + 1 = y, phương trình trở thành:

(y – 2)y²(y + 2) = 192 ⇔ y²(y² – 4) = 192

Đặt y² – 2 = z thì z + 2 ≥ 0, phương trình trở thành:

(z + 2)(z – 2) = 192 ⇔ z² = 196 ⇔ z = ±14

Loại z = -14 vì trái với điều kiện z + 2 ≥ 0

Với z = 14 thì y² = 16, do đó y = ±4

Với y = 4 thì x + 1 = 4 nên x = 3

Với y = -4 thì x + 1 = -4 nên x = -5

Vậy phương trình có nghiệm là {3; -5}.

Câu 106:

Thực hiện phép tính:

a) 17 – 25 + 55 – 17

b) 25 – (-75) + 32 – (32 + 75)

c) (-5).8.(-2).3

d) (-15) + (-122)

e) (7 – 10) + 3

f) |-127| – 18.(5 – 6)

Xem đáp án

a) 17 – 25 + 55 – 17

= (17 – 17) + (-25 + 55)

= 0 + 30

= 30

b) 25 – (-75) + 32 – (32 + 75)

= 25 + 75 + 32 – 32 – 75

= 25 + (75 – 75) + (32 – 32)

= 25 + 0 + 0

= 25

c) (-5).8.(-2).3

= (-5).(-2).8.3

= 10.8.3

= 80.3

= 240

d) (-15) + (-122)

= -15 – 122

= -137

e) (7 – 10) + 3

= 7 – 10 + 3

= (7 + 3) – 10

= 10 – 10

= 0

f) |-127| – 18.(5 – 6)

= 127 – 18.(-1)

= 127 + 18

= 145

Câu 107:

Tìm giá trị nhỏ nhất của C(x) = 3x² + x -1

Xem đáp án

C(x) = 3x² + x – 1

$\begin{array}{l} C (x) = 3 (x^{2} + \frac{1}{3} x - \frac{1}{3}) = 3 (x^{2} + 2 \cdot \frac{1}{6} x + \frac{1}{36} - \frac{1}{36} - \frac{1}{3}) \\ = 3 {(x + \frac{1}{6})}^{2} - \frac{3}{36} - \frac{3}{3} = 3 {(x + \frac{1}{6})}^{2} - \frac{13}{12} \end{array}$

Ta thấy: $3 {(x + \frac{1}{6})}^{2} \geq 0 \Rightarrow 3 {(x + \frac{1}{6})}^{2} - \frac{13}{12} \geq - \frac{13}{12}$

Dấu “ = ” xảy ra khi $x + \frac{1}{6} = 0 \Leftrightarrow x = - \frac{1}{6}$

Vậy min_C(x) = $- \frac{13}{2}$ khi x = $- \frac{1}{6}$

Câu 108:

Rút gọn các phân thức: $\frac{9 - {(x + 5)}^{2}}{x^{2} + 4 x + 4}$

Xem đáp án

$\begin{array}{l} \frac{9 - {(x + 5)}^{2}}{x^{2} + 4 x + 4} = \frac{(3 + x + 5) . (3 - x - 5)}{{(x + 2)}^{2}} \\ = \frac{(x + 8) (- x - 2)}{{(x + 2)}^{2}} = \frac{- (x + 8) (x + 2)}{{(x + 2)}^{2}} = \frac{- (x + 8)}{x + 2} \end{array}$

Câu 109:

Chứng minh rằng

\sqrt{a + b} \leq \sqrt{a} + \sqrt{b}

, với mọi a, b không âm

Xem đáp án

Hai vế của bất đẳng thức luôn không âm nên bình phương hai vế, ta được:

$\begin{array}{l} {(\sqrt{a + b})}^{2} \leq {(\sqrt{a} + \sqrt{b})}^{2} \\ \Leftrightarrow a + b \leq a + 2 \sqrt{a b} + b \end{array}$

$\Leftrightarrow 2 \sqrt{a b} \geq 0$ (luôn đúng).

Dấu “ = ” xảy ra khi a = 0 hoặc b = 0

Do đó $\sqrt{a + b} \leq \sqrt{a} + \sqrt{b}$ , với mọi a, b không âm.

Câu 110:

Cho hàm số y = f(x) thỏa mãn f’(x) = x² – 5x + 4. Khẳng định nào sau đây đúng?

A. Hàm số đã cho đồng biến trên khoảng (-∞; 3);

B. Hàm số đã cho nghịch biến trên khoảng (3; +∞);

C. Hàm số đã cho nghịch biến trên khoảng (2; 3);

D. Hàm số đã cho đồng biến trên khoảng (1; 4).

Xem đáp án

Đáp án đúng là: C

Ta có: f’(x) = x² – 5x + 4 = 0 $\Leftrightarrow [\begin{array}{l} x = 1 \\ x = 4 \end{array} \Rightarrow [\begin{array}{l} x \in (1; 4) \Rightarrow f' (x) < 0 \\ x \in (- \infty; 1) \cup (4; + \infty) \Rightarrow f' (x) > 0 \end{array}$

Do đó hàm số nghịch biến trên khoảng (1; 4) và đồng biến trên khoảng (-∞; 1) và (4;+∞).

Vì (2; 3) ⊂ (1; 4) suy ra hàm số đã cho nghịch biến trên khoảng (2; 3).

Vậy đáp án đúng là C.

Câu 111:

Cho hàm số $y = \frac{5 x + 9}{x - 1}$ . Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên khoảng (-∞; 1) ∪ (1; +∞);

B. Hàm số nghịch biến trên khoảng (-∞; 1) và (1; +∞);

C. Hàm số nghịch biến trên khoảng (-∞; 1) và (1; +∞);

D. Hàm số nghịch biến trên ℝ \ {1}.

Xem đáp án

Đáp án đúng là: B

Tập xác định: D = ℝ \ {1}.

$y = \frac{- 14}{{(x - 1)}^{2}} < 0$ , mọi x ∈ D ⇒ hàm số nghịch biến trên hai khoảng (-∞; 1) và (1; +∞)

Vậy đáp án đúng là B.

Câu 112:

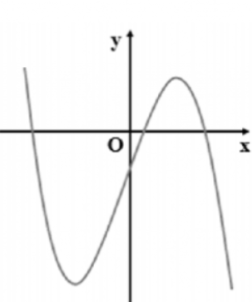
Cho hàm số y = ax³ + 3x + d (a, d ∈ ℝ) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

Media VietJack

A. a > 0, d > 0;

B. a < 0, d > 0;

C. a > 0, d < 0;

D. a < 0, d < 0.

Xem đáp án

Đáp án đúng là: D

Ta có: $\lim_{x \to + \infty} y = - \infty \Rightarrow$ đồ thị nhánh ngoài cùng của hàm số hướng đi xuống nên hệ số a < 0.

Giao điểm của đồ thị hàm số với trục tung Oy: x = 0 là điểm nằm bên dưới trục hoành nên khi x = 0 ⇒ y = d < 0

Vậy đáp án đúng là D.

Câu 113:

Cho hàm số y=f(x) có đồ thị trên một khoảng K như hình vẽ bên. Trên K, hàm số có bao nhiêu cực trị?

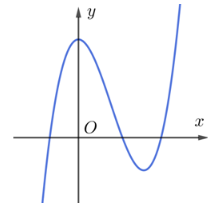
Media VietJack

A. 3;

B. 2;

C. 0;

D. 1.

Xem đáp án

Đáp án đúng là: B

Trên K, hàm số có 2 cực trị

Vậy đáp án đúng là B.

Câu 114:

Cho ∆ABC có Â < 90^o. Vẽ ra phía ngoài tam giác đó hai đoạn thẳng AD vuông góc và bằng AB; AE vuông góc và bằng AC.

a) Chứng minh: DC = BE và DC ⊥ BE

Xem đáp án

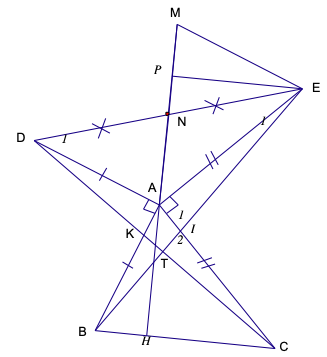
a) Ta có: AD = AB, AE = AC, $\hat{D A B} = \hat{E A C} = 90 °$

⇒ ∆DAC = ∆BAE (c.g.c) ⇒ DC = BE

Xét ∆AIE và ∆TIC:

Có I₁ và I₂ là hai góc đối đỉnh nên $\hat{I_{1}} = \hat{I_{2}}$

$\hat{A E I} = \hat{T C I}$ (do ∆DAC = ∆BAE)

$\Rightarrow \hat{E A I} = \hat{C T I} = 90 °$ ⇒ DC ⊥ BE

Câu 115:

b) Gọi N là trung điểm của DE. Trên tia đối của tia NA lấy M sao cho NA = NM. Chứng minh: AB = ME và ∆ABC = ∆EMA.

Xem đáp án

b) Xét ∆MNE và ∆AND có: NE = ND, NA = NM, $\hat{D N A} = \hat{M N E}$ (2 góc đối đỉnh)

⇒ ∆MNE = ∆AND (c.g.c) ⇒ $\hat{N D A} = \hat{M E N}$ và AD = ME

Mà AD = AB (gt) nên AB = ME (đpcm) (1)

Vì $\hat{N D A} = \hat{M E N}$ ⇒ DA // ME ⇒ $\hat{D A E} + \hat{E A M} = 180 °$ (hai góc trong cùng phía)

Mà $\hat{D A E} + \hat{B A C} = 180 ° \Rightarrow \hat{B A C} = \hat{A E M}$ (2)

Ta lại có: AC = AE (gt) (3)

Từ (1), (2), (3) ⇒ ∆ABC = ∆EMA (đpcm)

Câu 116:

c) Chứng minh: MA ⊥ BC.

Xem đáp án

c) Kéo dài MA cắt BC tại H. Từ E hạ EP ⊥ MH

Xét ∆AHC và ∆EPA có:

$\hat{C A H} = \hat{A E P}$ (Do cùng phía với $\hat{P A E}$ )

AE = CA (gt)

$\hat{H C A} = \hat{P A E}$ (Do ∆ABC = ∆EMA)

⇒ ∆AHC = ∆EPA (g.c.g)

$\Rightarrow \hat{E P A} = \hat{A H C} = 90 °$ ⇒ MA ⊥ BC (đpcm)

Câu 117:

Cho tam giác ABC vuông tại A với AB = a, AC = 2a quay xung quanh cạnh AB ta được một khối nón tròn xoay có đường sinh l bằng bao nhiêu ?

A. l = a $\sqrt{5}$ ;

B. l = a $\sqrt{3}$ ;

C. l = 3a;

D. l = 2a

\sqrt{2}

.

Xem đáp án

Đáp án đúng là: A

l = BC = $l = B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{a^{2} + 4 a^{2}} = \sqrt{5 a^{2}} = a \sqrt{5}$

Vậy đáp án đúng là A.

Câu 118:

Cho tam giác ABC với A(-3; 6); B(9; -10) và G $(\frac{1}{3}; 0)$ là trọng tâm. Tìm tọa độ điểm C

A. C(5; -4);

B. C(5; 4);

C. C(-5; 4);

D. C(-5; -4).

Xem đáp án

Đáp án đúng là: C

Ta có:

$\begin{array}{l} \{\begin{cases} x_{A} + x_{B} + x_{C} = 3 x_{G} \\ y_{A} + y_{B} + y_{C} = 3 y_{G} \end{cases} \Leftrightarrow \{\begin{cases} x_{C} = 3 x_{G} - (x_{A} + x_{B}) \\ y_{C} = 3 y_{G} - (y_{A} + y_{B}) \end{cases} \\ \{\begin{cases} x_{C} = 3. \frac{1}{3} - (- 3 + 9) \\ y_{C} = 3.0 - (6 + (- 10)) \end{cases} \Leftrightarrow \{\begin{cases} x_{C} = - 5 \\ y_{C} = 4 \end{cases} \end{array}$

⟹ C(-5; 4)

Vậy đáp án đúng là C.