Tính diện tích của mặt cầu ngoại tiếp hình tứ diện đều cạnh a.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
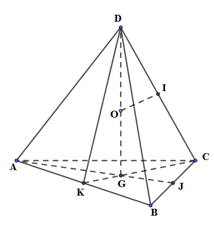
Xét tứ diện ABCD có cạnh đều bằng a. Gọi G là tâm tam giác ABC, I và J lần lượt là trung điểm của CD, BC
Dựng mặt trung trực của CD, cắt DG tại O. Khi đó O là tâm mặt cầu ngoại tiếp tứ diện ABCD.
∆DGC vuông tại G
∆DOI đồng dạng với ∆DCG
Diện tích mặt cầu là:
Vậy đáp án đúng là B
Hình nón có thiết diện qua trục là tam giác đều và có thể tích . Diện tích xung quanh S của hình nón đó là:
Cho đoạn thẳng AB và M là một điểm nằm trên đoạn AB sao cho AM = AB. Giá trị của k để có đẳng thức là:
Cho hình hộp ABCD.A’B’C’D’. Gọi M là điểm trên cạnh AC sao cho AC = 3MC. Lấy N trên cạnh C’D sao cho C’N = xC’D. Với giá trị nào của x thì MN // BD’.
Một hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước là 2 cm, 3 cm và 6 cm. Thể tích của khối tứ diện ACB’D’ bằng:
Cho tam giác ABC đều cạnh a. Gọi M là trung điểm BC. Khẳng định nào sau đây đúng?
Cho tứ diện ABCD có I, J lần lượt là trung điểm AC, BC. Gọi K thuộc BD sao cho KD < KB. Gọi E là giao điểm của JK và CD, F là giao điểm của AD và IE. Giao tuyến của (IJK) và (ACD) là:
Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Kẻ 2 tiếp tuyến AM, AN và cát tuyến ABC với đường tròn (AB < AC). Qua O kẻ OK vuông góc với BC tại K, OK cắt MN tại S. Chứng minh SC là tiếp tuyến của đường tròn (O).
Tính bán kính đường tròn giao tuyến của mặt cầu S(O;r) và mặt phẳng (α) biết rằng khoảng cách từ tâm O đến (α) bằng
Trong hệ trục tọa độ Oxy cho hình bình hành OABC, điểm C thuộc trục hoành. Khẳng định nào sau đây đúng?
Cho hình lăng trụ ABC.A'B'C' có thể tích là V. Gọi M là điểm thuộc cạnh CC' sao cho CM = 3C'M. Tính thể tích khối chóp M.ABC
Tìm m nguyên để hệ phương trình sau có nghiệm duy nhất là nghiệm nguyên.
a)