Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Kẻ 2 tiếp tuyến AM, AN và cát tuyến ABC với đường tròn (AB < AC). Qua O kẻ OK vuông góc với BC tại K, OK cắt MN tại S. Chứng minh SC là tiếp tuyến của đường tròn (O).
Giải bởi Vietjack
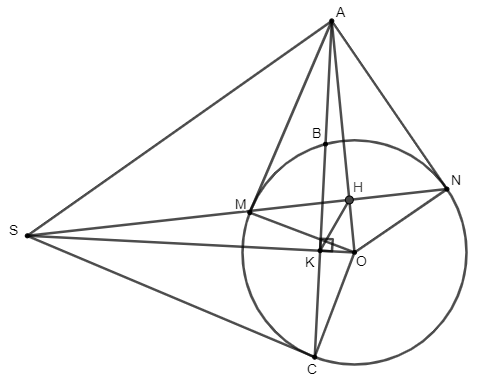
Gọi AO ∩ MN ≡ H
Theo tính chất hai tiếp tuyến cắt nhau: AM = AN
Mà OM = ON nên OA là trung trực của MN
Do đó OA ⊥ MN (1)
Mặt khác BC ⊥ OK ⟹ AC⊥ OS ⟹ (2)
Từ (1) và (2) suy ra tứ giác SKHA nội tiếp (hai góc cùng nhìn một cạnh bằng nhau)
Do đó theo tính chất tứ giác nội tiếp thì: OK.OS = OH.OA (*)
Vì AM là tiếp tuyến của đường tròn (O) nên AM ⊥ OM
Xét tam giác vuông AMO có đường cao MH, theo hệ thức lượng trong tam giác vuông thì: OC2 = R2 = OM2 = OH.OA (**)
Từ (*) và (**) ⟹ OC2 = OK.OS
Do đó tam giác OCK đồng dạng với tam giác OSC (cạnh – góc – cạnh)
⇒ SC ⊥ OC ⇒ SC là tiếp tuyến của đường tròn (O).
Cho đoạn thẳng AB và M là một điểm nằm trên đoạn AB sao cho AM = AB. Giá trị của k để có đẳng thức là:
Hình nón có thiết diện qua trục là tam giác đều và có thể tích . Diện tích xung quanh S của hình nón đó là:
Cho tam giác ABC đều cạnh a. Gọi M là trung điểm BC. Khẳng định nào sau đây đúng?
Một hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước là 2 cm, 3 cm và 6 cm. Thể tích của khối tứ diện ACB’D’ bằng:
Cho hình lăng trụ ABC.A'B'C' có thể tích là V. Gọi M là điểm thuộc cạnh CC' sao cho CM = 3C'M. Tính thể tích khối chóp M.ABC
Trong hệ trục tọa độ Oxy cho hình bình hành OABC, điểm C thuộc trục hoành. Khẳng định nào sau đây đúng?
Cho tứ diện ABCD có I, J lần lượt là trung điểm AC, BC. Gọi K thuộc BD sao cho KD < KB. Gọi E là giao điểm của JK và CD, F là giao điểm của AD và IE. Giao tuyến của (IJK) và (ACD) là:
