- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 8)
-
12907 lượt thi
-
115 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số y = x + 4 (d).
a) Vẽ đồ thị của hàm số trên mặt phẳng tọa độ Oxy
 Xem đáp án
Xem đáp án
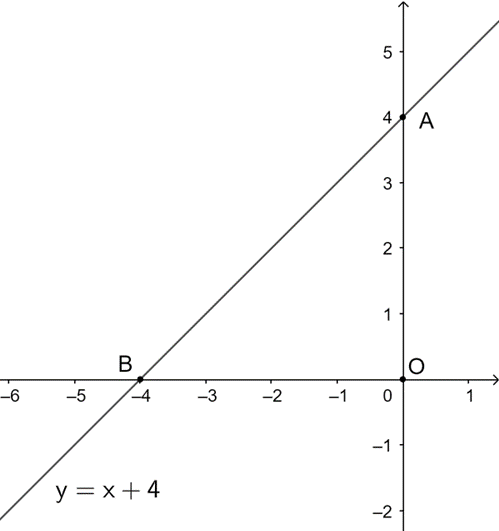
a) y = x + 4 (d).
• Với x = 0 => y = 4;
• Với y = 0 => x = −4.
Vậy đồ thị hàm số (d): y = x + 4 đi qua hai điểm A(0; 4) và B(−4; 0).
Câu 2:
b) Tính diện tích của ∆AOB (đơn vị đo trên các trục tọa độ là xen ti mét)
 Xem đáp án
Xem đáp án
b) Ta có OA = 4 và OB = 4.
Do đó, diện tích của ∆AOB là:
Câu 3:
 Xem đáp án
Xem đáp án
a) Để đồ thị hàm số (1) song song với đường thắng y = −x + 1 thì
m − 1 = −1 <=> m = 0.
Câu 4:
b) Xác định m để đường thắng y =1 − 3x , đường thẳng y = −0,5x − 1,5 và đồ thị hàm số (1) cùng đi qua một điểm.
 Xem đáp án
Xem đáp án
b) Hoành độ giao điểm của đường thắng y =1 − 3x , đường thẳng y = −0,5x − 1,5 là nghiệm của phương trình:
1 − 3x = −0,5x − 1,5
<=> 3x − 0,5x = 1 + 1,5
<=> 2,5x = 2,5
<=> x = 1
Với x = 1 => y = 1 − 3.1 = −2.
Vậy hai đường thẳng y =1 − 3x và y = −0,5x − 1,5 cắt nhau tại điểm M(1; −2).
Để đường thắng y =1 − 3x , đường thẳng y = −0,5x − 1,5 và đồ thị hàm số (1) cùng đi qua một điểm thì đồ thị hàm số (1) phải đi qua điểm M.
Suy ra −2 = (m − 1).1 + 3
<=> −2 = (m − 1) + 3 Û m = −4.
Câu 5:
Cho hàm số bậc nhất y = (m − 1)x + m − 3 (m ≠ 1) có đồ thị là đường thẳng d.
a) Khi m = 0, hãy vẽ đồ thị hàm số trên;
 Xem đáp án
Xem đáp án
a) Với m = 0 => y = − x − 3
Ta lập bảng:
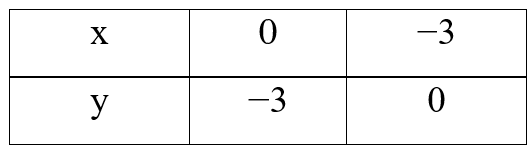
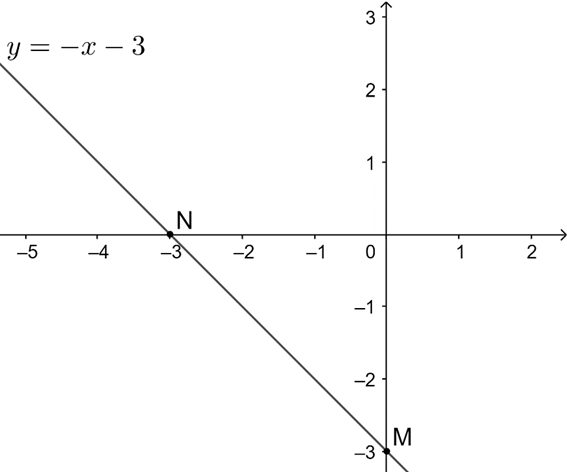
Hàm số y = − x − 3 đi qua hai điểm M(0; −3) và N(−3; 0).
Câu 6:
b) Tìm m để d cắt trục tung tại điểm có tung độ bằng 1;
 Xem đáp án
Xem đáp án
b) (d) cắt trục tung tại điểm có tung độ bằng 1
=> 1 = (m − 1).0 + m − 3
<=> 1 = m − 3
<=> m = 4.
Vậy m = 4 thì (d) cắt trục tung tại điểm có tung độ bằng 1.
Câu 7:
c) Gọi A, B lần lượt là giao điểm của d với hai trục Ox, Oy. Tìm m để tam giác OAB cân.
 Xem đáp án
Xem đáp án
c) Vì A là giao điểm của (d) với trục Ox nên yA = 0.
Khi đó (m − 1)xA + m − 3 = 0
B là giao điểm của (d) vưới trục Oy nên xB = 0
Khi đó yB = (m − 1).0 + m − 3 = m − 3
Để tam giác OAB cân tại O thì OA = OB
+) TH1:
<=> m(m − 3) = 0
+) TH2:
<=> (m − 2)(m − 3) = 0
Vậy các giá trị của m thỏa mãn là m = 1; m = 2; m = 3.
Câu 8:
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I (I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC (E khác B và C), AE cắt CD tại F. Chứng minh:
a) BEFI là tứ giác nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
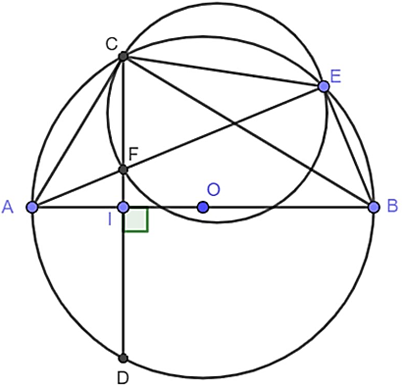
a) Tứ giác BEFI có: (giả thiết)
Suy ra I thuộc đường tròn đường kính BF.
(góc nội tiếp chắn nửa đường tròn)
Nên E thuộc đường tròn đường kính BF
=> BEFI nội tiếp đường tròn đường kính BF.
Câu 9:
 Xem đáp án
Xem đáp án
b) AB CD
• Xét ∆OCD cân có OI là đường cao nên cũng là đường trung tuyến, nên I là trung điểm của CD.
• Xét ∆ACD có AI vừa là đường cao vừa là đường trung tuyến nên ∆ACD cân tại đỉnh A nên AC = AD
=> (hai góc nội tiếp chắn hai cung bằng nhau)
Xét ∆ACF và ∆AEC có:
chung
(cmt)
=> ∆ACF ᔕ ∆AEC (g.g)
(hai cạnh tương ứng tỉ lệ)
=> AE . AF = AC2
Câu 10:
c) Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ∆CEF luôn thuộc một đường thẳng cố định.
 Xem đáp án
Xem đáp án
c) => AC là tiếp tuyến đường tròn ngoại tiếp ∆CEF (1)
Mặt khác (góc nội tiếp chắn nửa đường tròn)
=> AC CB (2)
Từ (1) và (2) suy ra CB chứa đường kính đường tròn ngoại tiếp ∆CEF
Mà CB cố định nên tâm đường tròn ngoại tiếp ∆CEF thuộc CB cố định khi E thay đổi trên cung nhỏ BC.
Câu 11:
Cho đường tròn (O) bán kính R, đường kính AB, vẽ dây cung CD vuông góc với AB (CD không đi qua (O)), trên tia đối của BA lấy S, SC cắt đường tròn tại M thuộc cung nhỏ BC
a) Chứng minh ∆SMA ᔕ ∆SBC.
 Xem đáp án
Xem đáp án
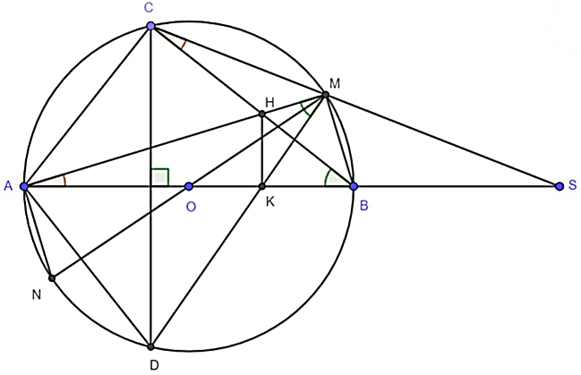
a) Xét ∆SMA và ∆SBC có:
chung
(Hai góc nội tiếp cùng chắn cung MB của (O))
=> ∆SMA ᔕ ∆SBC (g.g)
Câu 12:
b) Gọi H là giao điểm của MA và BC, K là giao điểm của MD và AB. Chứng minh tứ giác BMHK nội tiếp và HK // CD.
 Xem đáp án
Xem đáp án
b) Do CD AB (giả thiết)
=> AB là đường trung trực của CD (mối liên hệ giữa đường kính và dây cung)
=> AC = AD (tính chất đường trung trực)
(hai dây bằng nhau căng hai cung bằng nhau)
(góc nội tiếp cùng chắn hai cung bằng nhau)
Mà hai góc này cùng nhìn cạnh KH nên suy ra BMHK nội tiếp.
Câu 13:
 Xem đáp án
Xem đáp án
c) Kẻ đường kính MN
Xét ∆AON và ∆BOM có:
OA = OB = R
ON = OM = R
=> ∆AON = ∆BOM (c.g.c)
=> AN = BM (hai cạnh tương ứng bằng nhau)
(hai dây bằng nhau căng hai cung bằng nhau)
Ta có:
(tính chất góc có đỉnh nằm ngoài đường tròn) (1)
(tính chất góc nội tiếp)
(2)
Mà (3)
(4)
Từ (1), (2), (3) và (4) suy ra hay
Xét ∆OKM và ∆OMS có:
chung
(cmt)
=> ∆OKM ᔕ ∆OMS (g.g)
(hai cạnh tương ứng tỉ lệ)
=> OK.OS = OM2 = R2.
Câu 14:
Số đo các góc của một đa giác lồi có 9 cạnh lập thành một cấp số cộng có công sai d = 3°. Tìm số đo của các góc đó
 Xem đáp án
Xem đáp án
Tổng số đo các góc của đa giác lồi 9 cạnh là: (9 − 2).180° = 1260°
=> u1 = 128°.
Vậy số đo các góc là: 128°; 131°; 134°; 137°; 140°; 143°; 146°; 149°; 152°.
Câu 15:
 Xem đáp án
Xem đáp án
Chọn D
Tổng các góc của đa giác 9 cạnh bằng: (9 − 2) . 180° = 1260°.
Câu 16:
Viết phương trình đường thẳng đi qua 2 điểm A(1; 2) và B(3; 4).
 Xem đáp án
Xem đáp án
Ta có:
Phương trình đường thẳng qua A(1; 2) và có vectơ pháp tuyến là:
1(x − 1) − 1(y − 2) = 0
<=> x − y + 1 = 0.
Câu 17:
 Xem đáp án
Xem đáp án
Ta có:
Phương trình đường thẳng qua A(−1; −2) và có vectơ pháp tuyến là:
2(x + 1) + 1(y + 2) = 0
<=> 2x + y + 4 = 0.
Câu 18:
Xác định hàm số bậc hai thỏa mãn điều kiện.
a) Cho (P): y = ax2 + bx + c. Tìm a, b, c biết (P) đi qua điểm A(1; 2) và có đỉnh I(−1; −2).
 Xem đáp án
Xem đáp án
a) (P) đi qua điểm A(1; 2) nên ta có: a + b + c = 2 (1)
(P) có đỉnh I(−1; −2) nên ta có: a − b + c = −2 (2)
(P) có đỉnh là I(−1; −2) nên
=> −2a + b = 0 (3)
Từ (1), (2) và (3) ta có hệ phương trình:
Vậy a = 1; b = 2; c = −1.
Câu 19:
 Xem đáp án
Xem đáp án
b) (P): y = ax2 + bx − 3
Vì (P) có đỉnh là nên ta có hệ phương trình:
Vậy (P): y = 4x2 − 4x – 3.
Câu 20:
Tìm m để đồ thị hàm số y = x2 − mx + 1 đi qua điểm M(1; 2)
 Xem đáp án
Xem đáp án
Đồ thị hàm số đi qua điểm M(1; 2) nên ta có phương trình:
2 = 12 − m.1 + 1
<=> 2 − m = 2 <=> m = 0
Vậy m = 0 là giá trị cần tìm.
Câu 21:
Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau
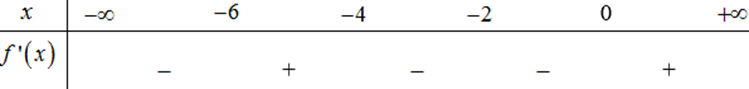
Hàm số f (2x − 2) − 2ex nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn A
Đặt g (x) = f (2x − 2) − 2ex ta có:
g '(x) = 2f '(2x − 2) − 2ex
= 2[f '(2x − 2) − ex]
Với x (0; 1) ta có:
=> g '(x) = 2[f '(2x − 2) − ex] < 0, ∀ x Î (0; 1)
=> Hàm số f (2x − 2) − 2ex nghịch biến trên khoảng (0; 1).
Câu 22:
Giải phương trình:
 Xem đáp án
Xem đáp án
2x2 + 3x + 9 = 36
<=> 2x2 + 3x − 27 = 0
<=> 2x2 − 6x + 9x − 27 = 0
<=> 2x(x − 3) + 9(x − 3) = 0
<=> (x − 3)(2x + 9) = 0
Vậy phương trình trên có hai nghiệm
Câu 23:
Phương trình có hai nghiệm là x1, x2. Tích x1x2 bằng:
 Xem đáp án
Xem đáp án
Chọn A
TXĐ: D = ℝ
(Do )
Bình phương 2 vế ta được:
2x2 + 3x + 9 = 36
<=> 2x2 + 3x − 27 = 0
<=> 2x2 − 6x + 9x − 27 = 0
<=> 2x(x − 3) + 9(x − 3) = 0
<=> (x − 3)(2x + 9) = 0
Vậy phương trình trên có hai nghiệm
Tích x1x2 bằng:
Câu 24:
Cho hàm số y = 3x − 2
a) Xác định các hệ số a, b. Tìm hai điểm thuộc đồ thị hàm số trên.
 Xem đáp án
Xem đáp án
a) Hàm số y = 3x − 2 có các hệ số a = 3 và b = −2.
Với x = 0 => y = 3.0 − 2 = − 2. Suy ra đồ thị hàm số đi qua điểm A(0; −2).
Với y = 0 => 3x − 2 = 0 . Suy ra đồ thị hàm số đi qua điểm
Câu 25:
b) Tìm m để đường thẳng y = 3x − 2 cắt đường thẳng y = mx + 2.
 Xem đáp án
Xem đáp án
b) Phương trình hoành độ giao điểm của hai đường thẳng y = 3x − 2 và y = mx + 2 là:
3x − 2 = mx + 2
<=> (m − 3)x = −4 (*)
Để đường thẳng y = 3x − 2 cắt đường thẳng y = mx + 2 thì phương trình (*) có 1 nghiệm => m ≠ 3.
Hoành độ giao điểm của hai đường thẳng là
Vậy với m ≠ 3 thì hai đường thẳng cắt nhau tại điểm có tọa độ
Câu 26:
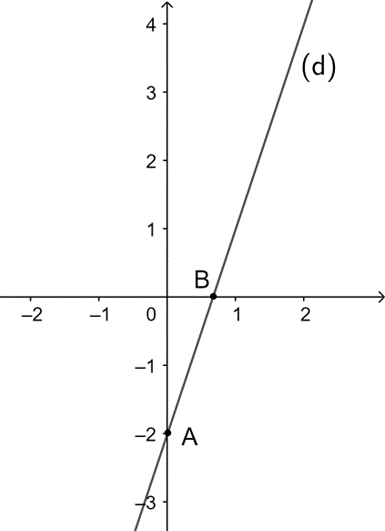
Cho hàm số y = 3x – 2. Vẽ đồ thị (d) của hàm số.
 Xem đáp án
Xem đáp án
Với x = 0 => y = 3.0 − 2 = − 2. Suy ra đồ thị hàm số đi qua điểm A(0; −2).
Với y = 0 => 3x − 2 = 0 . Suy ra đồ thị hàm số đi qua điểm
Đồ thị hàm số (d):
Câu 27:
Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm.
a) Tính BC, BH, HC, AH .
 Xem đáp án
Xem đáp án
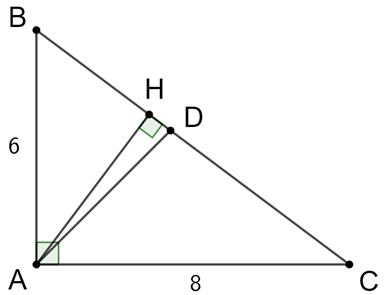
a) Vì ∆ABC vuông tại A nên ta có:
BC2 = AB2 + AC2
=> BC2 = 62 + 82 = 100
=> BC = 10 cm.
Áp dụng hệ thức lượng trong tam giác vuông, ta có:
Áp dụng hệ thức lượng trong tam giác vuông, ta có:
AB2 = BA.BC
<=> 62 = BH.10
=> HC = BC − BH = 10 − 3,6 = 6,4 (cm)
Vậy BC = 10 cm, BH = 3,6 cm, HC = 6,4 cm, AH = 4,8 cm.
Câu 30:
Cho ∆ABC vuông tại A vẽ đường cao AH có AB = 6 cm, AC = 8 cm.
a) Chứng minh ∆HBA ᔕ ∆ABC.
 Xem đáp án
Xem đáp án
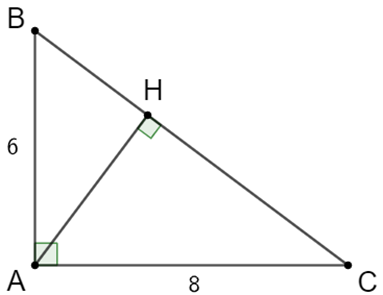
a) Xét ∆HBA và ∆ABC có:
chung
=> ∆HBA ᔕ ∆ABC (g.g).
Câu 31:
b) Tính BC, AH, HC.
 Xem đáp án
Xem đáp án
b) Áp dụng định lí Py-ta-go với ∆ABC vuông tại A nên ta có:
BC2 = AB2 + AC2
=> BC2 = 62 + 82 = 100
=> BC = 10 cm
∆HBA ᔕ ∆ABC
Áp dụng định lí Pytago vào ∆AHC vuông tại H nên ta có:
Câu 32:
c) Chứng minh AH2 = HB . HC.
 Xem đáp án
Xem đáp án
c) Xét ∆AHB và ∆CHA có:
(cùng phụ với )
=> ∆AHB ᔕ ∆CHA (g.g)
Câu 33:
 Xem đáp án
Xem đáp án
a) Số hạng tổng quát:
Ta có: x12y13 => k = 13.
Vậy hệ số của x12y13 trong khai triển (x + y)25 là
Câu 34:
b) Tìm hệ số của x12y13 trong khai triển (x − y)25.
 Xem đáp án
Xem đáp án
b) Số hạng tổng quát:
Ta có: x12y13 => k = 13
Vậy hệ số của x12y13 trong khai triển (x − y)25 là
Câu 35:
Tìm hệ số của x12y13 trong khai triển (2x + 3y)25.
 Xem đáp án
Xem đáp án
Ta có: x12y13 => k = 13.
Vậy hệ số của x12y13 trong khai triển (2x + 3y)25 là
Câu 36:
Cho hàm số bậc bốn f (x) có bảng biến thiên như sau:
![Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: Số điểm cực trị của hàm số g(x) = x2[f (x − 1)]4 là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/03/blobid10-1678117102.png)
Số điểm cực trị của hàm số g(x) = x2[f (x − 1)]4 là:
 Xem đáp án
Xem đáp án
Ta có:
g(x) = x2[f (x − 1)]4
=> g '(x) = 2x[f (x − 1)]4 + 4x2f '(x − 1)[f (x − 1)]3
<=> g '(x) = 2x[f (x − 1)]3[f (x − 1) + 2xf '(x − 1)] = 0
Đặt t = x − 1 => x = t + 1
Xét phương trình f (x − 1) = 0 <=> f (t) = 0
Dựa vào BBT ta thấy phương trình f (t) = 0 có 4 nghiệm phân biệt khác 1 nên phương trình f (x − 1) = 0 có 4 nghiệm phân biệt khác 0.
Xét phương trình f (x − 1) + 2xf '(x − 1) = 0
=> f (t) + 2(t + 1)f '(t) = 0 (*)
Dựa vào BBT ta thấy:
f (x) là hàm bậc bốn trùng phương, đặt f (x) = ax4 + bx2 + c (a ≠ 0)
Đồ thị hàm số đi qua 3 điểm (−1; 3), (0; −1), (1; 3) và có ba điểm cực trị x = 0, x = ±1 nên ta có:
=> f (x) = −4x4 + 8x2 − 1 => f '(x) = −16x3 + 16x.
Thay vào (*) ta có:
−4t4 + 8t2 − 1 + 2(t + 1)( −16t3 + 16t) = 0
<=> −4t4 + 8t2 − 1 − 32t4 + 32t2 − 32t3 + 32t = 0
<=> −36t4 − 32t3 + 40t2 + 32t − 1 = 0
Xét hàm số h (t) = −36t4 − 32t3 + 40t2 + 32t − 1 ta có:
h '(t) = − 144t3 − 96t2 + 80t + 32
Ta có:
Ta có BBT:
![Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: Số điểm cực trị của hàm số g(x) = x2[f (x − 1)]4 là: (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2023/03/blobid9-1678117023.png)
Dựa vào BBT ta thấy phương trình h (t) = 0 có 4 nghiệm phân biệt khác 1
=> Phương trình f (x − 1) − 2xf '(x − 1) = 0 có 4 nghiệm phân biệt khác 0.
Do đó, phương trình g '(x) = 0 có tất cả 9 nghiệm phân biệt.
Vậy hàm số g(x) = x2[f (x − 1)]4 có tất cả 9 điểm cực trị.
Câu 37:
Cho hàm số bậc bốn f (x) có bảng biến thiên như sau:
![Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: Số điểm cực trị của hàm số g(x) x4[f (x − 1)]2 là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/03/blobid11-1678117222.png)
Số điểm cực trị của hàm số g(x) = x4[f (x − 1)]2 là:
 Xem đáp án
Xem đáp án
Ta có: f (x) = 4x4 − 8x2 + 3 Þ f '(x) = 16x3 − 16x = 16x(x2 − 1)
Ta có g '(x) = 2x3f (x − 1)[2f (x − 1) + xf '(x − 1)]
Phương trình (1) có x = 0 (nghiệm bội ba).
Phương trình (2) có cùng số nghiệm với phương trình y = f (x) nên (2) có 4 nghiệm đơn.
Phương trình (3) có cùng số nghiệm với phương trình:
2f (x) + (x + 1)f '(x) = 0
<=> 2(4x4 − 8x2 + 3) + 16x(x + 1)(x2 − 1) = 0
<=> 24x4 + 16x3 − 32x2 − 16x + 6 = 0 có 4 nghiệm phân biệt.
Dễ thấy 9 nghiệm trên phân biệt nên hàm số g (x) = 0 có tất cả 9 điểm cực trị.
Câu 38:
Cho hàm số: y = x3 − 3mx2 + 9x + 1, có đồ thị (Cm), với m là tham số. Tìm giá trị của tham số m để đường thẳng (dm): y = x + 10 − 3m cắt đồ thị (Cm) tại 3 điểm phân biệt A, B, C. Gọi k1, k2, k3 là hệ số góc tiếp tuyến của (Cm) lần lượt tại A, B, C. Tìm giá trị của m để k1 + k2 + k3 > 15.
 Xem đáp án
Xem đáp án
y = x3 − 3mx2 + 9x + 1 => y' = 3x2 − 6mx + 9.
Phương trình hoành độ giao điểm của đồ thị (Cm) và đường thẳng (dm) là:
x3 − 3mx2 + 9x + 1 = x + 10 − 3m
<=> x3 − 3mx2 + 8x + 3m − 9 = 0
<=> (x3 + 8x − 9) − (3mx2 − 3m) = 0
<=> (x − 1)(x2 + x + 9) − 3m(x − 1)(x + 1) = 0
<=> (x − 1)[x2 + (1 − 3m)x + 9 − 3m] = 0
Cho A là điểm có hoành độ x1 = 1.
Suy ra hệ số góc tiếp tuyến của (Cm) tại A là k1 = 3.12 − 6m.1 + 9 = 12 − 6m
Để (Cm) cắt đường thẳng (dm) tại 3 điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt và khác 1.
Hoành độ của B và C là hai nghiệm của phương trình (*) với theo Vi-ét:
Hệ số góc tiếp tuyến của (Cm) tại B, C lần lượt là:
k2 = 3x22 − 6mx2 + 9 và k3 = 3x32 − 6mx3 + 9
Để k1 + k2 + k3 > 15
<=> (12 − 6m) + (3x22 − 6mx2 + 9) + (3x32 − 6mx3 + 9) > 15
<=> 3(x22 + x32) − 6m(x2 + x3) + 30 − 6m > 15
<=> 3[(x2 + x3)2 − 2x2x3] − 6m(x2 + x3) + 30 − 6m > 15
<=> 3[(3m − 1)2 − 2(9 − 3m)] − 6m(3m − 1) + 30 − 6m > 15
<=> 3(9m2 − 6m + 1 − 18 + 6m) − 18m2 + 6m + 30 − 6m > 15
<=> 9m2 > 36 Û m2 > 4
Kết hợp các điều kiện của m suy ra
Câu 39:
Giá trị nào của m để điểm I(−1; 6) là điểm cực đại của đồ thị hàm số y = x3 − 3mx2 − 9x + 1 (Cm).
 Xem đáp án
Xem đáp án
Ta có
Để I(−1; 6) là điểm cực đại của đồ thị hàm số y = x3 − 3mx2 − 9x + 1 (Cm) thì trước hết x = −1 là nghiệm của phương trình 3x2 − 6mx − 9 = 0
<=> 3(−1)2 − 6m(−1) − 9 = 0
<=> 3 + 6m − 9 = 0
<=> m = 1.
Thử lại với m = 1, ta được:
(Cm)
Khi đó với x = −1 ta có y = 6. Vây I(−1; 6) là điểm thuộc đồ thị hàm số.
Lại có
Ta xét BBT:
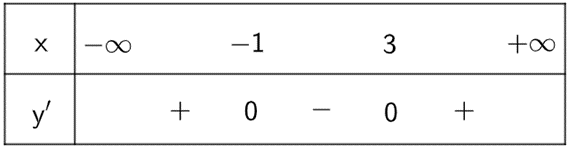
Dựa vào BBT ta thấy x = −1 là điểm cực địa của đồ thị hàm số
Vậy để điểm I(−1; 6) là điểm cực đại của đồ thị hàm số y = x3 − 3mx2 − 9x + 1 (Cm) thì m = 1.
Câu 40:
Tìm điều kiện của tham số m để hàm số là hàm số bậc nhất:
a)
 Xem đáp án
Xem đáp án
a) Để hàm số là hàm số bậc nhất nên suy ra:
Vậy m < 5 là giá trị của tham số m cần tìm.
Câu 41:
b)
 Xem đáp án
Xem đáp án
b) Để hàm số là hàm số bậc nhất nên suy ra:
Vậy m ≠ ±1 là giá trị của tham số m cần tìm.
Câu 42:
Cho hàm số: y = (m − 5)x + 1 (m là tham số).
a) Tìm m để hàm số trên là hàm số bậc nhất
 Xem đáp án
Xem đáp án
a) Để hàm số trên là hàm số bậc nhất thì:
m − 5 ≠ 0 <=> m ≠ 5.
Câu 43:
b) Với giá trị nào của m thì hàm số trên đồng biến; nghịch biến trên ℝ?
 Xem đáp án
Xem đáp án
b) Với m ≠ 5 thì y' = m – 5.
Để hàm số trên đồng biến thì y' = m − 5 > 0 <=> m > 5.
Để hàm số trên nghịch biến thì y' = m − 5 < 0 <=> m < 5.
Câu 44:
Cho tam giác ABC đều tâm O. M là điểm tùy ý trong tam giác. MD, ME, MF tương ứng vuông góc với BC, CA, AB. Chọn khẳng định đúng?
 Xem đáp án
Xem đáp án
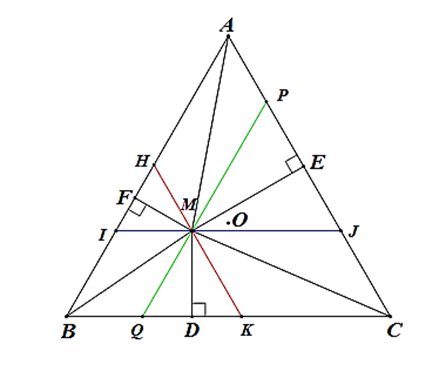
Qua M, kẻ các đường thẳng IJ // BC, HK // AC, PQ // AB.
∆ABC đều nên .
Mà PQ // AB nên ;
HK // AC nên
∆MQK có: nên là tam giác đều.
Lại có MD là đường cao kẻ từ M nên MD đồng thời là đường trung tuyến
Do đó D là trung điểm của QK.
(1)
Chứng minh tương tự ta cũng có:
+) (2)
+) (3)
Từ (1), (2) và (3) ta có:
Vì MI // BQ, MQ // BI nên tứ giác MIBQ là hình bình hành
Tương tự ta có:
Khi đó:
Lại có O là trọng tâm của tam giác ABC nên
Vậy
Câu 45:
Tìm số hạng thứ năm trong khai triển mà trong khai triển đó số mũ của x giảm dần.
 Xem đáp án
Xem đáp án
Số hạng thứ k + 1 trong khai triển là:
Vậy
Câu 46:
Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của (1 + 2x)10 là?
 Xem đáp án
Xem đáp án
Số hạng thứ k + 1 trong khai triển là:
Vậy số hạng đầu tiên là:
Số hạng thứ hai là:
Số hạng thứ ba là:
Câu 47:
 Xem đáp án
Xem đáp án
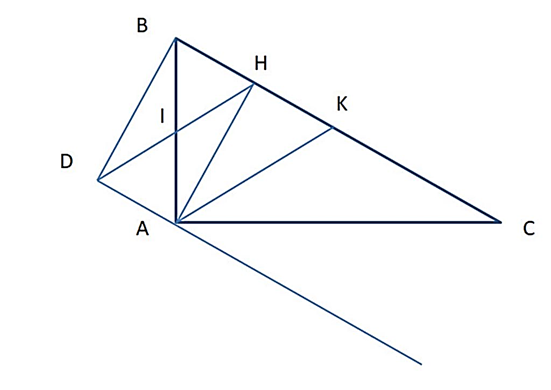
a) Xét ∆BAK có:
I là trung điểm của AB;
H là trung điểm của BK.
=> IH là đường trung bình của ∆BAK
=> IH // AK.
Xét tứ giác ADHK có: DH // AK và AD // HK nên suy ra ADHK là hình bình hành.
Câu 48:
b) CM tứ giác AHBD là hình chữ nhật. Từ đó tính diện tích tứ giác AHBD nếu AH = 6 cm, AB = 10 cm
 Xem đáp án
Xem đáp án
b) Do AKHD là hình bình hành suy ra HK // AD và HK = AD.
Mà HK = BH (gt) và H, K Î BC
=> BH // AD và BH = AD.
Xét tứ giác AHBD có: BH // AD và BH = AD
=> AHBD là hình bình hành.
Mà AH CB hay
=> AHBD là hình chữ nhật.
Xét ∆ABH vuông ở H có:
AH2 + BH2 = AB2
<=> 62 + BH2 = 102
<=> BH2 = 64
=> BH = 8 (cm)
Xét hình chữ nhật AHBD có diện tích là:
8 . 6 = 48 (cm2).
Câu 49:
Tập nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Điều kiện:
Khi đó:
(*)
Với x = 4 => log (x − 3) = 4 − x = 0 nên x = 4 là nghiệm của phương trình (*).
Với x > 3 suy ra log (x − 3) là hàm đồng biến mà 4 − x là hàm nghịch biến nên suy ra phương trình chỉ có một nghiệm duy nhất x = 4.
Câu 50:
Tập nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Điều kiện:
Khi đó:
<=> x2 − 6x + 7 = x − 3
<=> x2 − 7x + 10 = 0
<=> (x − 2)(x − 5) = 0
Vậy tập nghiệm của phương trình là S = {5}.
Câu 51:
a) Vẽ đồ thị của các hàm số đã cho trên cùng một hệ trục tọa độ Oxy.
 Xem đáp án
Xem đáp án
a) +) y = x + 3 (d1)
Với x = 0 => y = 3. Suy ra (d1) đi qua điểm có tọa độ A(0; 3).
+) y = 3x + 7 (d2).
Với x = 0 => y = 7. Suy ra (d2) đi qua điểm có tọa độ B(0; 7).
+) Hoành độ giao điểm của hai đường thẳng (d1) và (d2) là nghiệm của phương trình:
x + 3 = 3x + 7
<=> x = −2 => y = 1
Vậy giao điểm của hai đường thẳng (d1) và (d2) là J(−2; 1).

Câu 52:
 Xem đáp án
Xem đáp án
b) I là trung điểm của đoạn thẳng AB nên ta có:
=> I(0; 5)
Câu 53:
c) Gọi J là giao điểm của hai đường thẳng (d1) và (d2). Chứng minh tam giác OIJ là tam giác vuông. Tính diện tích của tam giác đó.
 Xem đáp án
Xem đáp án
c) Ta có:
(đvđd);
(đvđd).
Suy ra IJ2 + OJ2 = OI2.
Theo định lí Pytago đảo nên suy ra ∆OIJ là tam giác vuông tại J.
Vậy diện tích tam giác OIJ là:
(đvdt).
Câu 54:
Cho 2 đường thẳng: và (d2): y = −x + 2.
Gọi A, B lần lượt là giao điểm của (d1) và (d2) với trục Ox, C là giao điểm của (d1), (d2). Tính chu vi và diện tích của tam giác ABC (đơn vị trên hệ trục tọa độ là cm).
 Xem đáp án
Xem đáp án
• Vì A là giao điểm của (d1) với trục Ox nên
=> A(−4; 0).
• Vì B là giao điểm của (d2) với trục Ox nên −x + 2 = 0 <=> x = 2
=> B(2; 0).
• Vì C là giao điểm của (d1), (d2) nên => y = 2
=> C(0; 2)
Ta có:
(đvđd);
(đvđd);
AB = 6 (đvđd); OC = 2 (đvđd).
Chu vi của tam giác ABC là:
(đvđd)
Diện tích tam giác ABC là:
(đvdt).
Câu 55:
a) Vẽ đồ thị khi m = 2.
 Xem đáp án
Xem đáp án
a) Với m = 2 => y = x + 4 (d)
Với x = 0 => y = 4. Suy ra đồ thị đi qua điểm có tọa độ (0; 4)
Với y = 0 => x = −4. Suy ra đồ thị đi qua điểm có tọa độ (−4; 0)
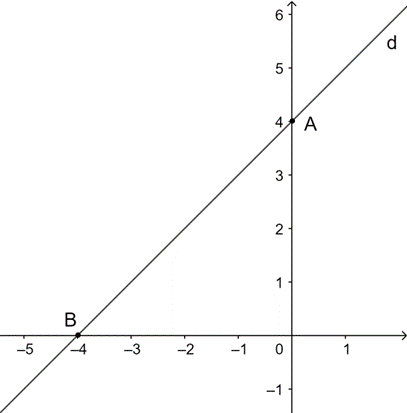
Câu 56:
 Xem đáp án
Xem đáp án
b) Để (d) song song với đồ thị hàm số y = −3x + 2 (d1)
=> m − 1 = −3 <=> m = −2
Vậy m = −2 là giá của m thỏa mãn.
Câu 57:
c) Tìm m để (d) cắt đồ thị hàm số y = x − 7 (d2) tại 1 điểm nằm bên trái trục tung.
 Xem đáp án
Xem đáp án
c) Hoành độ giao điểm của (d) và (d2) là nghiệm của phương trình:
(m − 1)x + 4 = x − 7
<=> (m − 2)x = −11.
Để (d) cắt đồ thị hàm số y = x − 7 (d2) tại 1 điểm nằm bên trái trục tung thì:
Vậy m > 2 là giá trị của m thỏa mãn.
Câu 58:
Cho hàm số bậc nhất y = (m − 1)x + 4 có đồ thị là đường thẳng (d) (m là tham số và m ≠ 1).
a) Vẽ đồ thị khi m = 2.
 Xem đáp án
Xem đáp án
a) Với m = 2 => y = x + 4 (d).
Với x = 0 => y = 4. Suy ra đồ thị đi qua điểm có tọa độ (0; 4).
Với y = 0 => x = −4. Suy ra đồ thị đi qua điểm có tọa độ (−4; 0).
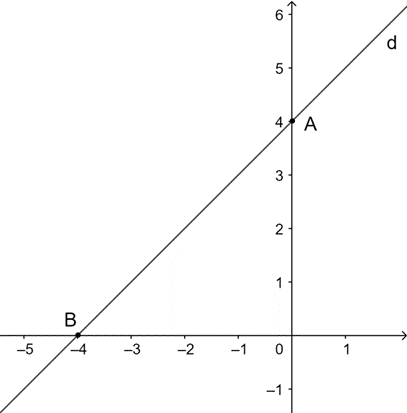
Câu 59:
b) Với giá trị nào của m thì đường thẳng (d) song song với đường thẳng y = −3x + 2 (d1).
 Xem đáp án
Xem đáp án
b) Để (d) song song với đồ thị hàm số y = −3x + 2 (d1)
=> m − 1 = −3 <=> m = −2
Vậy m = −2 là giá của m thỏa mãn.
Câu 60:
c) Tìm m để đường thẳng (d) cắt trục Ox, Oy lần lượt tại hai điểm A, B sao cho diện tích tam giác OAB bằng 2.
 Xem đáp án
Xem đáp án
c) Đường thẳng (d) cắt trục Ox tại điểm có hoành độ
Đường thẳng (d) cắt trục Oy tại điểm có tung độ y = 4
=> B(0; 4) => OB = 4.
Khi đó diện tích của tam giác OAB là:
Vậy m = −3 và m = 5 là giá trị cần tìm thỏa mãn của tham số m.
Câu 61:
ho đường tròn (O; R) và một điểm A sao cho OA = 2R, vẽ các tiếp tuyến AB, AC với (O; R), B và C là các tiếp điểm. Vẽ đường kính BOD.
a) Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn.
 Xem đáp án
Xem đáp án
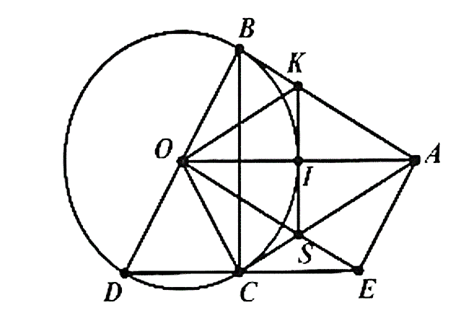
a) Ta có AB và AC là tiếp tuyến của (O)
Xét tứ giác ABOC có:
Suy ra tứ giác ABOC là tứ giác nội tiếp đường tròn.
Hay A, B, O, C thuộc 1 đường tròn.
Câu 62:
b) Chứng minh rằng: DC // OA.
 Xem đáp án
Xem đáp án
b) Ta có: AB và AC là tiếp tuyến của (O) => AB = AC.
Mà OB = OC = R => OA là đường trung trực của BC hay OA BC (1)
Xét ∆CBD nội tiếp (O) có BD là đường kính của (O).
Suy ra ∆CBD vuông tại C hay DC BC (2)
Từ (1), (2) => DC // OA.
Câu 63:
c) Đường trung trực của BD cắt AC và CD lần lượt tại S và E. Chứng minh rằng OCEA là hình thang cân.
 Xem đáp án
Xem đáp án
c) Ta có: DC // OA => CE // OA => OCEA là hình thang (3)
Ta có:
Suy ra
Xét ∆BOA và ∆ODE có:
(cmt)
OB = OD = R
=> ∆BOA = ∆ODE (g.c.g)
=> AB = OE (hai cạnh tương ứng)
Mà AB = AC (AB và AC đều là tiếp tuyến chung của (O))
Suy ra OE = AC (4)
Từ (3) và (4) => OCEA là hình thang cân.
Câu 64:
d) Gọi I là giao điểm của đoạn OA và (O), K là giao điểm của tia SI và AB. Tính theo R diện tích tứ giác AKOS.
 Xem đáp án
Xem đáp án
d) Ta có:
Suy ra => ∆SOA cân tại S
Lại có SI là đường trung tuyến
Suy ra SI OA => KS OA (5)
Ta có ∆KAS có
AI KS suy ra KI = SI.
Mà OI AI
Suy ra OKAS là hình bình hành (6)
Từ (5) và (6) suy ra AKOS là hình thoi.
Ta có ∆OAB vuông tại A có OA = 2OD = 2R
Vậy
Câu 65:
Giải phương trình nghiệm nguyên 12x2 + 6xy + 3y2 = 28(x + y)
 Xem đáp án
Xem đáp án
12x2 + 6xy + 3y2 = 28(x + y)
<=> 3y2 + 2y(3x − 14) + 12x2 − 28x = 0 (1)
Ta xem (1) là phương trình bậc hai ẩn y thì (1) có nghiệm nguyên khi ∆' là số chính phương
Ta có: ∆' = (3x − 14)2 − 3(12x2 − 28x) = −27x2 + 196 (2)
=> −27x2 + 196 = k2 ≥ 0 => 27x2 196
<=> x2 7
Mà x ℤ nên x {0; ±1; ±2}.
Lần lượt thử các giá trị của x vào (2) ta có:
+) Với x = 0 => ∆' = 196 = 142 (thỏa mãn) nên khi đó phương trình (1) trở thành
(1) <=> 3y2 − 28y = 0
+) Với x = ±1 => ∆' = 169 = 132 (thỏa mãn) nên khi đó
x = 1, phương trình (1) trở thành
(1) <=> 3y2 − 22y − 16 = 0
• Với x = −1, phương trình (1) trở thành
(1) <=> 3y2 − 34y + 40 = 0
•Với x = ±2 => ∆' = 88 (không thỏa mãn) nên khi đó không cho y là số nguyên.
Vậy cặp nghiệm nguyên (x; y) thỏa mãn là {(0; 0), (1; 8), (−1; 10)}.
Câu 66:
Cho và tia Ou là tia đối của tia Ov. Khi đó hai góc được gọi là hai góc gì? Và góc bằng bao nhiêu độ?
 Xem đáp án
Xem đáp án
Ta có tia Ou là tia đối của tia Ov nên là hai góc kề bù.
Suy ra
Câu 67:
Viết tên các cặp góc phụ nhau, bù nhau có trong hình sau:
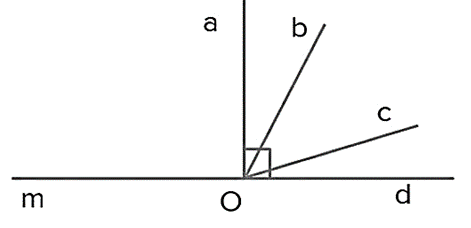
 Xem đáp án
Xem đáp án
• Hai góc phụ nhau là hai góc có tổng số đo bằng 90°. Vì vậy, trong hình vẽ có các cặp góc nhụ nhau là:
và
và
• Hai góc bù nhau là hai góc có tổng số đo bằng 180°. Vì vậy, trong hình vẽ có các cặp góc bù nhau là:
và
và
và
Câu 68:
Cho a2 + b2 + c2 = ab + bc + ca. Chứng minh a = b = c
 Xem đáp án
Xem đáp án
Ta có: a2 + b2 + c2 = ab + bc + ca
<=> 2(a2 + b2 + c2) = 2(ab + bc + ca)
<=> 2a2 + 2b2 + 2c2 = 2ab + 2bc + 2ca
<=> (a2 − 2ab + b2) + (b2 − 2bc + c2) + (c2 − 2ca + a2) = 0
<=> (a − b)2 + (b − c)2 + (c − a)2 = 0
Mà (a − b)2 ≥ 0; (b − c)2 ≥ 0; (c − a)2 0 nên suy ra
(đpcm)
Câu 69:
Chứng minh bất đẳng thức: a2 + b2 + c2 ≥ ab + bc + ca.
 Xem đáp án
Xem đáp án
Giả sử a2 + b2 + c2 ≥ ab + bc + ca
<=> 2(a2 + b2 + c2) ≥ 2(ab + bc + ca)
<=> 2a2 + 2b2 + 2c2 ≥ 2ab + 2bc + 2ca
<=> (a2 − 2ab + b2) + (b2 − 2bc + c2) + (c2 − 2ca + a2) ≥ 0
<=> (a − b)2 + (b − c)2 + (c − a)2 ≥ 0
Mà (a − b)2 ≥ 0; (b − c)2 ≥ 0; (c − a)2 ≥ 0 nên suy ra
(a − b)2 + (b − c)2 + (c − a)2 ≥ 0 (luôn đúng)
Vậy a2 + b2 + c2 ≥ ab + bc + ca (đpcm).
Câu 70:
Cho phương trình x2 − 2(m + 3)x + m2 − 1 = 0.
Tìm m để Q = x1 + x2 − 3x1x2 có giá trị lớn nhất.
 Xem đáp án
Xem đáp án
x2 − 2(m + 3)x + m2 − 1 = 0
Ta có: ∆' = (m + 3)2 − (m2 − 1) = 6m + 10
Để phương trình có hai nghiệm phân biệt thì ∆' > 0
Hay 6m + 10 > 0
Theo hệ thức Vi-ét ta có:
Xét Q = x1 + x2 − 3x1x2 = 2(m + 3) − 3(m2 − 1)
= −3m2 + 2m + 9
Dấu “=” xảy ra <=> (thỏa mãn)
Vậy là giá trị của m thỏa mãn.
Câu 71:
Cho phương trình: x2 − mx + m − 1 = 0 (1). Tìm m để phương trình (1) có hai nghiệm phân biệt x1 và x2 thoả mãn: x12 + 3x1x2 = 3x2 + 3m + 16.
 Xem đáp án
Xem đáp án
• Xét phương trình: x2 − mx + m − 1 = 0 (1)
Ta có: ∆ = m2 − 4(m − 1) = m2 − 4m + 4 = (m − 2)2
Để phương trình có hai nghiệm phân biệt thì ∆ > 0
Hay (m − 2)2 > 0 <=> m ≠ 2
Theo hệ thức Vi-ét ta có:
• Xét phương trình: x12 + 3x1x2 = 3x2 + 3m + 16 (2)
+) TH1:
Khi đó phương trình (2) trở thành:
(2) <=> (m − 1)2 + 3(m − 1) = 3 + 3m + 16
<=> m2 − 2m − 21 = 0
+) TH2:
Khi đó phương trình (2) trở thành:
(2) <=> 12 + 3(m − 1) = 3(m − 1) + 3m + 16
<=> 3m + 15 = 0
<=> m = −5.
Vậy và m = −5 là các giá trị của m thỏa mãn.
Câu 72:
Tìm giá trị nhỏ nhất của biểu thức sau: A = 4x2 + 4x + 11.
 Xem đáp án
Xem đáp án
A = 4x2 + 4x + 11
<=> A = 4x2 + 4x + 1 + 10
<=> A = (2x + 1)2 + 10
Vì (2x + 1)2 ≥ 0 nên (2x + 1)2 + 10 ≥ 10.
Dấu “=” xảy ra khi và chỉ khi 2x + 1 = 0
Vậy GTNN của A = 10 khi
Câu 73:
Tìm giá trị nhỏ nhất của A = 4x2 − 4x + 11.
 Xem đáp án
Xem đáp án
A = 4x2 − 4x + 11
<=> A = 4x2 − 4x + 1 + 10
<=> A = (2x − 1)2 + 10
Vì (2x − 1)2 ≥ 0 nên (2x − 1)2 + 10 ≥ 10
Dấu “=” xảy ra khi và chỉ khi 2x − 1 = 0
Vậy GTNN của A = 10 khi
Câu 74:
Giải phương trình nghiệm nguyên: x2 + 2xy = 5y + 6.
 Xem đáp án
Xem đáp án
x2 + 2xy = 5y + 6
<=> x2 + 2xy + y2 = y2 + 5y + 6 (1)
<=> (x + y)2 = (y + 2)(y + 3).
Vì (x + y)2 bằng tích của hai số nguyên liên tiếp là (y + 2) và (y + 3) nên một trong hai số (y + 2) và (y + 3) phải có một số bằng 0.
Khi đó:
• Với y + 2 = 0 <=> y = −2 => x = 2;
• Với y + 3 = 0 <=> y = −3 => x = 3.
Vậy cặp nghiệm nguyên (x; y) của phương trình là {(2; −2); (3; −3)}.
Câu 75:
 Xem đáp án
Xem đáp án
x2 − 2xy + 5y2 = y + 1 (1)
<=> x2 − 2xy + y2 = −4y2 + y + 1
<=> (x − y)2 = −4y2 + y + 1
Vì (x − y)2 ≥ 0 nên −4y2 + y + 1 ≥ 0
Suy ra
Vì y ℤ => y = 0.
Với y = 0 thì phương trình (1) trở thành:
(1) <=> x2 = 1 <=> x = ±1.
Vậy cặp nghiệm nguyên (x; y) của phương trình là {(1; 0); (−1; 0)}.
Câu 77:
Chứng minh bất đẳng thức: a2 + b2 + c2 ≥ ab + bc + ca.
 Xem đáp án
Xem đáp án
Giả sử a2 + b2 + c2 ≥ ab + bc + ca
<=> 2(a2 + b2 + c2) ≥ 2(ab + bc + ca)
<=> 2a2 + 2b2 + 2c2 ≥ 2ab + 2bc + 2ca
<=> (a2 − 2ab + b2) + (b2 − 2bc + c2) + (c2 − 2ca + a2) ≥ 0
<=> (a − b)2 + (b − c)2 + (c − a)2 ≥ 0
Mà (a − b)2 ≥ 0; (b − c)2 ≥ 0; (c − a)2 ≥ 0 nên suy ra
(a − b)2 + (b − c)2 + (c − a)2 ≥ 0 (luôn đúng)
Vậy a2 + b2 + c2 ≥ ab + bc + ca (đpcm).
Câu 78:
Chứng minh a2 + b2 + c2 < 2(ab + bc + ca) với mọi số thực a, b, c là độ dài ba cạnh của một tam giác.
 Xem đáp án
Xem đáp án
Vì a, b, c là độ dài ba cạnh của một tam giác nên ta có:
0 < a < b + c => a2 < a(b + c) = ab + ca;
0 < b < c + a => b2 < b(c + a) = bc + ab;
0 < c < a + b => c2 < c(a + cb) = ca + bc
Do đó suy ra a2 + b2 + c2 < (ab + ca) + (bc + ab) + (ca + bc)
=> a2 + b2 + c2 < 2(ab + bc + ca).
Câu 79:
 Xem đáp án
Xem đáp án
Áp dụng BĐT AM - GM ta có:
(1)
(2)
(3)
Cộng vế theo vế của (1), (2), (3) nên ta có:
Theo hệ quả của BĐT AM - GM thì:
Do đó
Dấu “=” xảy ra khi a = b = c > 0
Câu 80:
Cho a, b, c > 0 thỏa a2 + b2 + c2 = 3. CMR:
 Xem đáp án
Xem đáp án
BĐT trên tương đương với việc chứng minh
Áp dụng BĐT AM - GM ta có:
(1)
(2)
(3)
Cộng vế theo vế của (1), (2), (3) nên ta có:
(*)
Chia 2 vế của (*) với abc > 0 ta suy ra:
(đpcm).
Dấu “=” xảy ra khi a = b = c = 1.
Câu 81:
Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có BC = 3, góc = 30°. Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
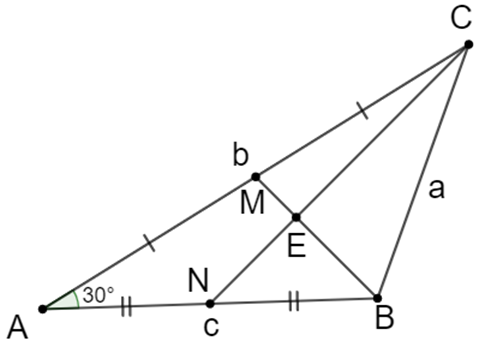
Gọi E là giao điểm của BM và CN.
Ta có công thức đường trung tuyến:
Trong tam giác ABC có: BM CN nên tam giác CEB vuông tại E
=> CE2 + BE2 = BC2
Tam giác ABC có:
a2 = b2 + c2 − 2bc.cos A = 5a2 − 2bc.cos A
Khi đó:
Câu 82:
 Xem đáp án
Xem đáp án
Ta có:
<=> BC2 − BC − 20 = 0
<=> (BC − 5)(BC + 4) = 0
Vậy BC = 5 cm.
Câu 84:
 Xem đáp án
Xem đáp án
Chọn C
<=> (1)
Phương trình (1) có 3 nghiệm phân biệt
=> Đường thẳng y = −m cắt đồ thị hàm số y = x3 − 12x − 2 tại 3 điểm phân biệt.
Xét hàm số f (x) = x3 − 12x − 2 => f '(x) = 3x2 − 12 = 0
<=> x = ± 2.
Ta có BBT của hàm số f (x) = x3 − 12x − 2 với tập xác định là ℝ
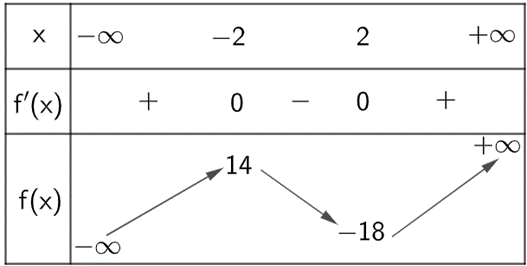
Dựa vào BBT ta có: −18 < −m < 14 <=> −14 < m < 18.
Câu 85:
Tìm m để phương trình sau có 3 nghiệm phân biệt: x3 − 6x2 + 3(m + 2)x − m − 6 = 0.
 Xem đáp án
Xem đáp án
x3 − 6x2 + 3(m + 2)x − m − 6 = 0
<=> x3 − 6x2 + 3mx + 6x − m − 6 = 0
<=> x3 − 6x2 + 6x − 6 = m(1 − 3x) (1)
• TH1: 1 − 3x = 0
Khi đó, phương trình (*) trở thành (vô nghiệm).
• TH2: 1 ≠ 3x = 0
Khi đó, phương trình (1) trở thành (*)
Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số y = f (x) và đường thẳng y = m.
Ta có:
<=> 2x3 − 7x2 + 4x + 4 = 0
<=> (2x + 1)(x − 2)2 = 0
Ta có BBT:
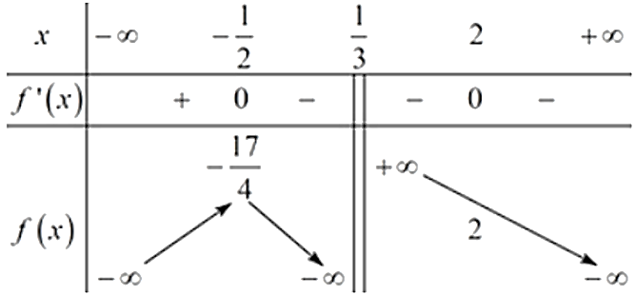
Dựa vào BBT ta thấy phương trình (*) có 2 nghiệm phân biệt khi và chỉ khi
Câu 86:
b) Gọi E là giao điểm của AD và đường tròn (O) (E khác D), H là giao điểm của OA và BC. Chứng minh rằng: AE.AD = AH.AO.
 Xem đáp án
Xem đáp án
b) ∆ECD nội tiếp đường tròn (O) có CD là đường kính.
=> ∆ECD vuông tại E => CE ED
∆ACO vuông tại C có CH là đường cao
Theo hệ thức lượng trong tam giác vuông ta có:
AH.AO = AC2 (3)
∆ACD vuông tại C có CE là đường cao
Theo hệ thức lượng trong tam giác vuông ta có:
AE.AD = AC2 (4)
Từ (3) và (4) suy ra AE.AD = AH.AO.
Câu 87:
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng OA vuông góc với BC.
 Xem đáp án
Xem đáp án
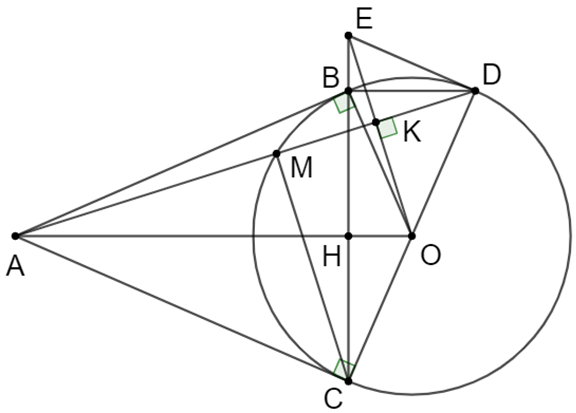
a) Ta có: AB = AC (Tính chất của hai tiếp tuyến cắt nhau);
OB = OC = R.
=> OA là đường trung trực của BC => OA BC (1)
Câu 88:
b) Vẽ đường kính CD. Chứng minh rằng BD // AO.
 Xem đáp án
Xem đáp án
b) ∆BCD nội tiếp đường tròn (O) có CD là đường kính.
=> ∆BCD vuông tại B => BD BC (2)
Từ (1) và (2) suy ra OA // BD.
Câu 89:
c) Tính độ dài các cạnh của tam giác ABC, biết OB = 2 cm; OA = 4 cm.
 Xem đáp án
Xem đáp án
c) • Xét ∆OBA vuông tại O. Áp dụng định lí Py-ta-go, ta có:
• Xét ∆ABO vuông tại B có BH là đường cao.
Theo hệ thức lượng trong tam giác vuông, ta có:
BH . AO = AB . BO
Câu 90:
d) Đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là M.
Chứng minh: AM.AD = AH.AO.
 Xem đáp án
Xem đáp án
d) ∆MCD nội tiếp đường tròn (O) có CD là đường kính.
=> ∆MCD vuông tại M => CM MD
• Xét ∆ACO vuông tại C có CH là đường cao
Theo hệ thức lượng trong tam giác vuông ta có:
AH . AO = AC2 (3)
• Xét ∆ACD vuông tại C có CM là đường cao
Theo hệ thức lượng trong tam giác vuông, ta có:
AM . AD = AC2 (4)
Từ (3) và (4) suy ra AM . AD = AH . AO.
Câu 91:
e) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại E. Chứng minh ED là tiếp tuyến của đường tròn (O).
 Xem đáp án
Xem đáp án
e) Ta có: OE AD, BD BC
=> Tứ giác BKDE nội tiếp.
Mà
=> A, B, K, O, C cùng thuộc đường tròn đường kính AO
=> ED là tiếp tuyến của (O).
Câu 92:
Cho hình thang cân ABCD. Đáy nhỏ AB bằng cạnh bên BC và đường chéo AC vuông góc với cạnh bên AD.
a) Tính các góc của hình thang cân.
 Xem đáp án
Xem đáp án
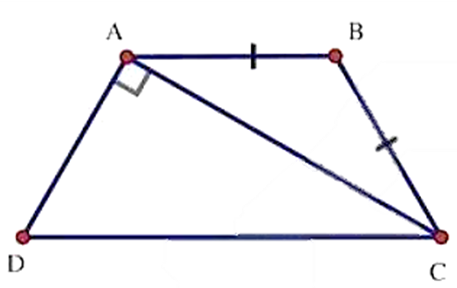
a) ABCD là hình thang cân
• Xét ∆ACD có:
• Xét ∆ABC có: AB = BC => ∆ABC cân tại B
Ta có:
Mà
Câu 93:
b) Chứng minh rằng trong hình thang cân đó đáy lớn gấp đôi đáy nhỏ.
 Xem đáp án
Xem đáp án
b) Xét ∆ADC có
Trong một tam giác vuông, cạnh đối diện với góc 30° có độ dài bằng nửa cạnh huyền
Suy ra
Mà
Câu 94:
Cho hình thang ABCD có đáy lớn AD, đường chéo AC vuông góc với cạnh bên CD, . Tính AD nếu chu vi của hình thang bằng 20 cm và góc
 Xem đáp án
Xem đáp án

Tia AB cắt DC tại E.
=> AC là tia phân giác của (gt)
AC CD => AC DE.
Tam giác ADE có AC là đường cao vừa là đường phân giác nên ∆ADE là tam giác cân tại A.
Lại có: ΔADE là tam giác đều.
=> C là trung điểm của DE (Do AC đồng thời là trung tuyến) .
Mà: BC // AD => BC là đường trung bình của ΔADE.
Ta có:
Giả thiết: AB + BC + CD + AD = 20
Câu 95:
Chứng minh rằng x2002 + x2000 + 1 chia hết cho x2 + x + 1.
 Xem đáp án
Xem đáp án
Ta có:
A = x2002 + x2000 + 1 = x2002 + x2001 + x2000 − (x2001 − 1)
= x2000(x2 + x + 1) − [(x3)667 − 1]
= x2000(x2 + x + 1) − (x3 − 1)[(x3)666 + (x3)665 + … + 1]
= x2000(x2 + x + 1) − (x − 1)(x2 + x + 1)[(x3)666 + (x3)665 + … + 1]
= (x2 + x + 1){x2000 − (x − 1)[(x3)666 + (x3)665 + … + 1]}.
Vây x2002 + x2000 + 1 chia hết cho x2 + x + 1.
Câu 96:
Tìm x để x2 + x + 1 chia hết cho x – 1.
 Xem đáp án
Xem đáp án
Ta có:
A = x2 + x + 1 = x2 − x + 2x − 2 + 3
= x(x − 1) + 2(x − 1) + 3
= (x + 2)(x − 1) + 3.
Vì (x + 2)(x − 1) ⋮ (x − 1) nên để x2 + x + 1 ⋮ x − 1 thì 3 ⋮ (x − 1).
Vậy x − 1 Ư(3) = {±1; ±3} => x = {−2; 0; 2; 4}.
Câu 97:
a) Chứng minh: ∆OBA vuông tại B và ∆OAK cân tại K.
 Xem đáp án
Xem đáp án
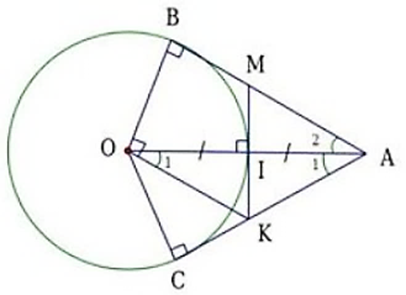
a) AB là đường tiếp tuyến của đường tròn (O)
=> OB BA => ∆OBA vuông tại B.
Ta có: AB OB (1)
OK OB (2)
Từ (1) và (2) suy ra AB // OK
=> (so le trong).
Mà (Tính chất hai tiếp tuyến cắt nhau)
Vậy ∆OKA cân tại K.
Câu 98:
 Xem đáp án
Xem đáp án
b) Ta có: KM và (O) có điểm chung là I (3)
Mặt khác: OI = R, OA = 2R => IA = R
=> KI là trung tuyến của ∆OKA
Mà ∆OKA cân tại K (cmt)
=> KI OA hay KM OI (4)
Từ (3) và (4) => KM là tiếp tuyến của (O).
Câu 99:
c) Tính chu vi tam giác AMK theo R.
 Xem đáp án
Xem đáp án
c) ∆AMK cân tại A (AI vừa là đường cao vừa là đường phân giác)
=> AM = AK
Khi đó, ∆AMK là tam giác đều
Do đó, chu vi ∆AMK là:
Câu 100:
Cho đường tròn (O; R) và điểm A cách O một khoảng 2R. Từ A vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Đường thảng vuông góc với B tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.
a) Chứng minh: AMON là hình thoi.
 Xem đáp án
Xem đáp án
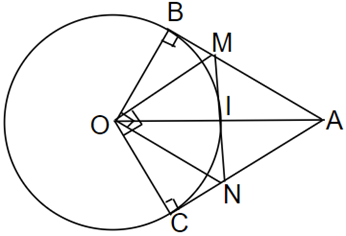
a) Do AB là tiếp tuyến của (O) => OB AB
Mà OB ON (gt) => AB // ON hay AM // ON (1)
Do AC là tiếp tuyến của (O) => OC AC
Mà OC OM (gt) => AC // OM hay AN // OM (2)
Từ (1) và (2) nên suy ra AMON là hình thoi
Câu 101:
b) Chứng minh: MN là tiếp tuyến của đường tròn.
 Xem đáp án
Xem đáp án
b) Đặt I là trung điểm của OA
Hay OI là bán kính của (O).
Do AMON là hình thoi nên suy ra OA MN tại I.
Hay OI MN tại I.
Mà OI là bán kính của (O) => MN là tiếp tuyến của (O).
Câu 102:
c) Tính diện tích AMON.
 Xem đáp án
Xem đáp án
c) Xét tam giác OAB có OA AB.
(Hai góc ở vị trí so le trong).
Xét hình thoi AMON có OA cắt MN tại I => I là trung điểm MN.
Hay IN = IM =
Xét tam giác ION có
Câu 103:
 Xem đáp án
Xem đáp án
Câu 104:
Cho nửa đường tròn (O), đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K, B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP // KM. Gọi Q là giao điểm của các đường thẳng AP và BM; E là giao điểm của PB và AM.
a) Chứng minh rằng tứ giác PQME nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
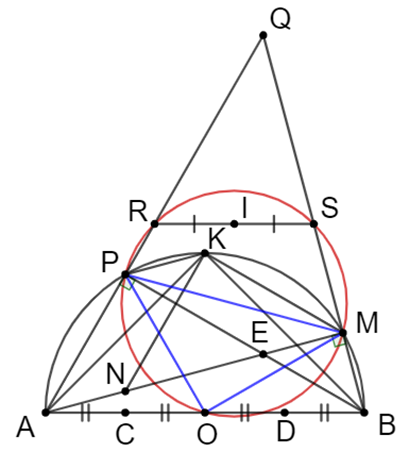
a) Xét đường tròn tâm O, đường kính AB có:
(góc nội tiếp chắn nửa đường tròn).
Nên (hai góc kề bù với hai góc trên).
Suy ra
Do đó, tứ giác PQME nội tiếp đường tròn.
Câu 105:
b) Chứng minh: ∆AKN = ∆BKM.
 Xem đáp án
Xem đáp án
b) K là điểm chính giữa cung AB nên
=> AK = KB (liên hệ giữa cung và dây)
Xét ∆AKN và ∆BKM có:
AK = BK (cmt)
(Hai góc nội tiếp cùng chắn cung KM)
AN = BM (gt)
=> ∆AKN = ∆BKM (c.g.c).
Câu 106:
c) Chứng minh: AM . BE = AN . AQ.
 Xem đáp án
Xem đáp án
c) Xét ∆AMQ và ∆BME có:
(Hai góc nội tiếp cùng chắn cung MP)
=> ∆AMQ ᔕ ∆BME (g.g)
Mà AN = BM => AM.BE = AN.AQ
Câu 107:
d) Gọi R, S lần lượt là giao điểm thứ hai của QA, QB với đường tròn ngoại tiếp ∆OMP. Chứng minh rằng khi M di động trên cung KB thì trung điểm I của RS luôn nằm trên một đường cố định
 Xem đáp án
Xem đáp án
d) (ABMP nội tiếp)
(RPMS nội tiếp)
(Hai góc ở vị trí đồng vị)
=> RS // AB
BP // KM =>
=>
(Hai góc ở tâm chắn hai cung bằng nhau)
=> ∆OMP nội tiếp đường tròn đường kính PM
PQME nội tiếp đường tròn nên suy ra
Kẻ IC // AQ, ID // BQ
RS = OM = OA = OB = R (không đổi)
=> C, D là trung điểm của OA, OB Þ C, D cố định
I luôn nhìn CD cố định dưới góc 45°
=> I nằm trên cung chứa góc 45° vẽ trên đoạn CD cố định.
Câu 108:
Cho nửa đường tròn (O) đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K; B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP song song với KM. Gọi Q là giao điểm của các đường thẳng AP, BM.
a) So sánh hai tam giác: ΔAKN và ΔBKM.
 Xem đáp án
Xem đáp án
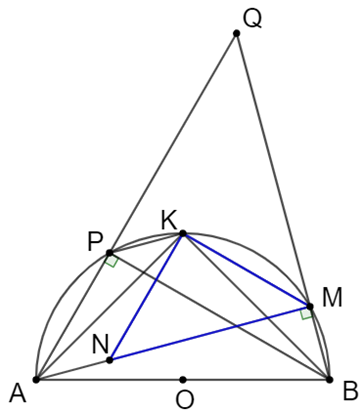
a) K là điểm chính giữa cung AB nên
=> AK = KB (liên hệ giữa cung và dây)
Xét ∆AKN và ∆BKM có:
AK = BK (cmt)
(Hai góc nội tiếp cùng chắn cung KM)
AN = BM (gt)
=> ∆AKN = ∆BKM (c.g.c)
Câu 109:
b) Chứng minh: ΔKMN vuông cân.
 Xem đáp án
Xem đáp án
b) ∆AKN = ∆BKM
và KN = KM
Khi đó:
Mà KN = KM (cmt)
=> ∆KMN là tam giác vuông cân tại K
Câu 110:
c) Tứ giác ANKP là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
c) Vì K nằm chính giữa cung AB với AB là đường kính
Mà BP // KM => KMBP là hình thang cân
=> KB = PM
Mà
=> PK // AM
Lại có PK = MB = AN => ANKP là hình bình hành.
Câu 111:
Cho tam giác ABC có , AB = AC, điểm D thuộc cạnh AB. Đường thẳng qua B và vuông góc với CD cắt đường thẳng CA ở K. Chứng minh rằng AK = AD
 Xem đáp án
Xem đáp án
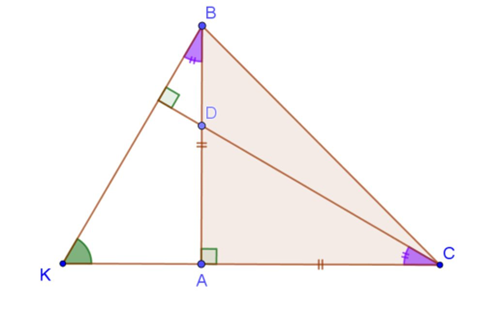
Xét ∆AKB vuông tại A và ∆ADC vuông tại A, ta có:
AB = AC (gt)
(cùng phụ với )
=> ∆AKB = ∆ADC (cạnh góc vuông - góc nhọn).
=> AK = AD (hai cạnh tương ứng).
Câu 112:
 Xem đáp án
Xem đáp án
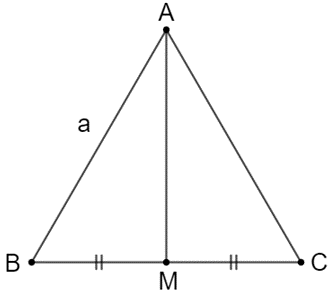
= 2AC.AB.cos 60° − 3AC2
Câu 114:
Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 8.
 Xem đáp án
Xem đáp án
a) Số phần tử của không gian mẫu là:
Gọi A là biến cố “Số chấm trên mặt hai lần gieo có tổng bằng 8”.
Gọi số chấm trên mặt khi gieo lần một là x.
Số chấm trên mặt khi gieo lần hai là y.
Theo bài ra, ta có:
=> (x; y) = {(2; 6), (3; 5), (4; 4), (6; 2), (5; 3)}.
Khi đó số kết quả thuận lợi của biến cố là:
Vậy xác suất cần tính làCâu 115:
b) Tích số chấm hai mặt xuất hiện là số lẻ.
 Xem đáp án
Xem đáp án
b) Số phần tử của không gian mẫu là:
Gọi B là biến cố “Tích số chấm trên mặt hai lần gieo là số lẻ”.
Gọi số chấm trên mặt khi gieo lần một là x.
Số chấm trên mặt khi gieo lần hai là y.
Theo bài ra, ta có:
=> x, y = {1; 3; 5}.
Khi đó, số kết quả thuận lợi của biến cố là:
Vậy xác suất cần tính là