Thứ hai, 16/12/2024
Đăng ký Đăng nhập
IMG-LOGO
Trang chủ Lớp 12 Toán Trắc nghiệm tổng hợp môn Toán 2023 có đáp án

Trắc nghiệm tổng hợp môn Toán 2023 có đáp án

Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 73)

  • 11354 lượt thi

  • 23 câu hỏi

  • 39 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Chia 50 cái kẹo cho 10 em bé, em nào cũng được chia kẹo. Chứng minh rằng dù cách chia thế nào cũng tồn tại 2 em bé có số kẹo như nhau.
Xem đáp án

Ta có nếu mỗi em bé đều có kẹo

Nếu em bé có một cái là ít nhất thì 10 em bé tổng cộng cần số kẹo là

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55 > 5.

Vậy có ít nhất 2 em có số kẹo như nhau.

Câu 2:

Cho tam giác ABC nhọn nội tiếp đường tròn tâm O (AB < AC), đường kính AD. Đường cao BE, CP, AQ cắt nhau tại H.

a) Chứng minh rằng tứ giác APHE nội tiếp.

b) So sánh \(\widehat {BAH}\) và \(\widehat {OAC}\).
Xem đáp án
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O (AB < AC), đường kính AD (ảnh 1)

a)

Xét tam giác ABC có:

CP là đường cao nên CP vuông góc với AB hay \(\widehat {CPA} = 90^\circ \)

BE là đường cao nên BE vuông góc với AC hay \(\widehat {BEA} = 90^\circ \)

Xét tứ giác APHE có:

\(\widehat {APH} = \widehat {CPA} = 90^\circ \)

\(\widehat {AEH} = \widehat {BEA} = 90^\circ \)

\( \Rightarrow \widehat {APH} + \widehat {AEH} = 180^\circ \)

Do đó, tứ giác APHE nội tiếp.

b)

Điểm C thuộc đường tròn đường kính AD nên \(\widehat {ACD} = 90^\circ \)

Xét đường tròn tâm O, \(\widehat {ABC} = \widehat {ADC}\) (góc nội tiếp cùng chắn cung nhỏ AC)

Xét tam giác ABQ và tam giác ADC có:

\(\widehat {AQB} = \widehat {ACD} = 90^\circ \)

\(\widehat {ABQ} = \widehat {ABC} = \widehat {ADC}\) (cmt)

Do đó, tam giác ABE và tam giác ADC đồng dạng (g.g)

\( \Rightarrow \widehat {BAH} = \widehat {OAC}\).

Câu 3:

Chị hỏi bố: "Năm nay mẹ bao nhiêu tuổi?".

Bố trả lời: "Lấy tuổi bố, tuổi mẹ và tuổi con cộng lại bằng 60 tuổi. Tuổi bố gấp 6 lần tuổi con, đến khi tuổi bố gấp đôi tuổi con thì tổng số tuổi của ba người gấp đôi tuổi ba người hiện nay".

Hỏi hiện nay mẹ bao nhiêu tuổi ?
Xem đáp án

Khi tuổi bố gấp đôi tuổi con thì tổng ba người gấp đôi hiện nay và bằng :

60 × 2 = 120 ( tuổi )

Khi đó tổng 3 người hơn tổng hiện nay là:

120 – 60 = 60 ( tuổi )

Vậy lúc đó là thời điểm sau thời điểm hiện tại là:

60 : 3 = 20 (năm) (chia 3 vì cả ba đều tăng số tuổi như nhau)

Vậy hiện nay tuổi bố gấp 6 lần tuổi con, sau đây 20 năm thì tuổi bố gấp 2 lần tuổi con.

Ta thấy hiệu tuổi bố và tuổi con luôn không thay đổi (1)

Hiện nay, bố : con = 6 : 1 ⇒ Bố 6 phần, con 1 phần, hiệu 5 phần.

Hiệu bằng 5 lần tuổi con hiện nay (2)

Sau 20 năm nữa, bố : con = 2 : 1 ⇒ Bố 2 phần, con 1 phần, hiệu 2 phần.

Hiệu bằng tuổi con sau 20 năm nữa (3)

Từ (1), (2) và (3) suy ra: (tuổi con sau 20 năm) = 5 lần (tuổi con hiện nay)

Gọi (tuổi con hiện nay) là 1 phần, thì (tuổi con sau 20 năm) sẽ là 5 phần.

Hiệu số phần là:

5 – 1 = 4 (phần)

4 phần này tương ứng với 20 năm nên 1 phần là

20 : 4 = 5 (tuổi)

Vậy tuổi con hiện nay là 5 tuổi. Tuổi bố gấp 6 lần nên tuổi bố là 5 × 6 = 30 (tuổi)

Tuổi mẹ là:

60 – 5 – 30 = 25 (tuổi)

Đáp số: Con 5 tuổi, Bố 30 tuổi, Mẹ 25 tuổi.

Câu 4:

Xem hình vẽ, cho biết a song song b và c vuông góc với a.

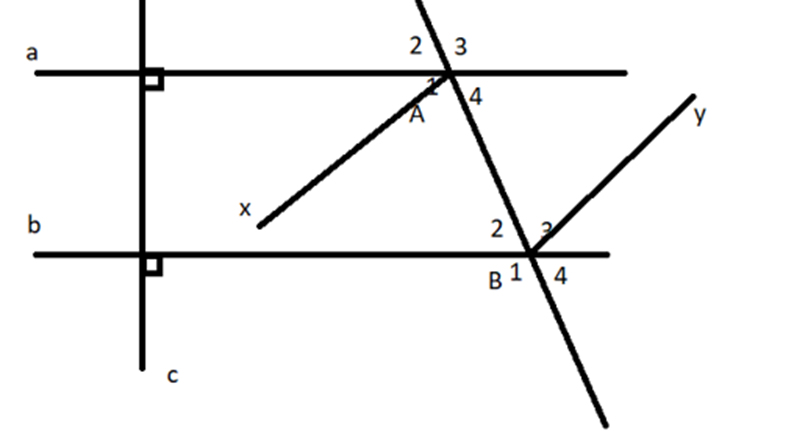
Cho đường thẳng d cắt hai đường thẳng a và b tại A và B. Cho biết góc A1 = 115 độ (ảnh 1)

a) Cho đường thẳng d cắt hai đường thẳng a và b tại A và B. Cho biết góc \(\widehat {{A_1}} = 115^\circ \). Tính số đo các góc \(\widehat {{B_2}},\widehat {{B_3}},\widehat {{A_3}}\).

b) Gọi Ax và By lần lượt là tia phân giác của các góc \(\widehat {{A_1}}\) và \(\widehat {{B_3}}\). Chứng minh: Ax song song By.
Xem đáp án

a)

a song song với b nên \(\widehat {{A_1}} = \widehat {{B_1}} = 115^\circ \) (đồng vị)

\(\widehat {{B_1}} = \widehat {{B_3}} = 115^\circ \) (đối đỉnh)

\(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) (kề bù)

\( \Rightarrow \widehat {{B_2}} = 180^\circ - \widehat {{B_1}} = 180^\circ - 115^\circ = 65^\circ \)

\[\widehat {{B_2}} = \widehat {{B_4}} = 65^\circ \] (đối đỉnh)

b)

Do Ax là phân giác nên \(\widehat {xAB} = \frac{1}{2}\widehat {{A_1}};\widehat {yBA} = \frac{1}{2}\widehat {{B_3}}\)

Mà \(\widehat {{A_1}} = \widehat {{B_3}}\) (hai góc so le)

\( \Rightarrow \widehat {xAB} = \widehat {yBA}\)

Do đó, Ax song song với By (hai góc so le bằng nhau).

5700. có bao nhiêu cách sắp xếp 3 người đàn ông và 2 người đàn bà ngồi trên một chiếc ghế dài sao (vietjack)

Câu 5:

Có bao nhiêu cách sắp xếp 2 người đàn ông và 3 người phụ nữ ngồi trên một chiếc ghế dài sao cho 2 người cùng phái phải ngồi gần nhau.
Xem đáp án

Đặt vị trí trên ghế là 1, 2, 3, 4 và 5.

Trường hợp 1: Ghế số 1 là người đàn ông ngồi, vậy sắp xếp là Nam – Nam – Nữ – Nữ – Nữ

Vị trí 1: có 2 cách xếp (chọn 1 trong 2 người đàn ông)

Vị trí 2: có 1 cách xếp

Vị trí 3: có 3 cách xếp (chọn 1 trong 3 người phụ nữ)

Vị trí 4: có 2 cách xếp

Vị trí 5: 1 cách xếp

Theo quy tắc nhân:

2 . 1 . 3 . 2 . 1 = 12 cách xếp.

Trường hợp 2: Ghế số 1 là người phụ nữ ngồi, vậy sắp xếp là: Nữ – Nữ – Nữ – Nam – Nam

Tương tự ta có

3 . 2 . 1 . 2 . 1 = 12 cách xếp

Vậy có tổng số

12 + 12 = 24 cách xếp.

Câu 6:

Một mảnh vườn hình chữ nhật có chiều rộng 12 m,chiều dài bằng \(\frac{3}{2}\) chiều rộng. Tính diện tích mảnh vườn hình chữ nhật đó.

Xem đáp án

Chiều dài mảnh vườn hình chữ nhật là: \(12 \times \frac{3}{2} = 18\) (m).

Diện tích mảnh vườn hình chữ nhật là: 18 × 12 = 216 (m2).

Đáp số: 216 m2.

Câu 7:

Dũng và Minh có tổng cộng 64 viên bi, biết rằng nếu Dũng cho Minh 8 viên bi thì số bi của hai bạn bằng nhau. Hỏi mỗi bạn có bao nhiêu viên bi ?
Xem đáp án

Dũng có số viên bi là:

64 : 2 + 8 = 40 (viên)

Minh có số viên bi là:

64 – 40 = 24 (viên)

Đáp số: Dũng 40 viên bi, Minh 24 viên bi.

Câu 8:

Tính giá trị biểu thức: M = x4 – 2x3 + 3x2 – 2x + 2 với x2 – x = 4.
Xem đáp án

M = x4 – 2x3 + 3x2 – 2x + 2

= x4 – x3 – x3 + x2 + 2x2 – 2x + 3

= x2(x2 – x) – x(x2 – x) + 2(x2 – x) + 2

= (x2 – x)(x2 – x + 2) + 2

Thay x2 – x = 4 vào M ta được:

M = 4.(4 + 2) + 2 = 26.

Câu 9:

So sánh \(A = \frac{{{{100}^{100}} + 1}}{{{{100}^{99}} + 1}}\) và \(B = \frac{{{{100}^{99}} + 1}}{{{{100}^{89}} + 1}}\).
Xem đáp án

Ta có:

\(A = \frac{{{{100}^{100}} + 1}}{{{{100}^{99}} + 1}} > 1 \Rightarrow A > \frac{{{{100}^{100}} + 1 + 99}}{{{{100}^{90}} + 1 + 99}} = \frac{{{{100}^{100}} + 100}}{{{{100}^{90}} + 100}} > \frac{{100\left( {{{100}^{99}} + 1} \right)}}{{100\left( {{{100}^{89}} + 1} \right)}} = B\)

Vậy A > B.

Câu 10:

Viết số bé nhất có 5 chữ số và có tổng các chữ số bằng 40.
Xem đáp án

Ta có 9 × 4 = 36 < 40 và 9 × 5 = 45 > 40, do đó số cần viết phải có 4 chữ số 9, để tổng các chữ số bằng 40 thì chữ số thứ 5 là 40 – 36 = 4. Để nó là số bé nhất thì 4 phải là chữ số đầu tiên bên trái.

Vậy số cần tìm là: 49 999.

Câu 11:

Tìm x, biết:

a) (x + 4)(x2 – 4x + 16) – x(x – 5)(x + 5) = 264;

b) (x – 2)3 – (x – 2)(x22 + 2x + 4) + 6(x – 2)(x + 2) = 60.
Xem đáp án

a) (x + 4)(x2 – 4x + 16) – x(x – 5)(x + 5) = 264

⇔ (x + 4)(x2 – 4x + 42) – x(x2 – 52) = 264

⇔ x3 + 43 – x3 + 25x = 264

⇔ 25x = 200

⇔ x = 8.

b) (x – 2)3 – (x – 2)(x22 + 2x + 4) + 6(x – 2)(x + 2) = 60

⇔ x3 – 6x2 + 12x – 8 – (x3 – 23) + 6(x2 – 4) = 60

⇔ x3 – 6x2 + 12x – 8 – x3 + 8 + 6x2 – 24 = 60

⇔ 12x = 84

⇔ x = 7.

Câu 12:

Tìm ba số biết tổng của số thứ nhất và số thứ hai bằng 50, tổng của số thứ hai và số thứ ba là 42, tổng của số thứ nhất và số thứ ba là 56.
Xem đáp án

Ta có:

ST1 + ST2 = 50

ST2 + ST3 = 42

ST3 + ST1 = 56

Tổng của 3 số trên là: (50 + 42 + 56) : 2 = 74

Số thứ 1 là: 74 – 42 = 32

Số thứ 2 là: 50 – 32 = 18

Số thứ 3 là: 42 – 18 = 24.

Câu 13:

Cho bảng sau.

1

2

4

7

4

?

7

10

6

?

?

12

7

8

10

?

 

Hỏi bảng trên còn thiếu những số nào?
Xem đáp án

Quy luật:

2 – 1 = 1

4 – 2 = 2

7 – 4 = 3

Dãy số trên cách đều 1; 2; 3… đơn vị

Ta có:

4 + 1 = 5

6 + 1 = 7

7 + 2 = 9

10 + 3 = 13

Vậy ta có:

1

2

4

7

4

5

7

10

6

7

9

12

7

8

10

13

Câu 14:

80 phút = bao nhiêu giờ (viết dưới dạng phân số)?
Xem đáp án

80 phút = \(\frac{{80}}{{60}} = \frac{4}{3}\) giờ.

Câu 15:

Cho \(A = 3 + {3^2} + {3^3} + ... + {3^{2009}}\). Tìm số tự nhiên n, biết rằng 2A + 3 = 3n.
Xem đáp án

\(\begin{array}{l}A = 3 + {3^2} + {3^3} + ... + {3^{2009}}\\ \Rightarrow 3A = {3^2} + {3^3} + ... + {3^{2010}}\\ \Rightarrow 3A - A = {3^{2010}} - 3\\ \Rightarrow 2A = {3^{2010}} - 3\\ \Rightarrow 2A + 3 = {3^{2010}}\\ \Rightarrow n = 2010\end{array}\)

Câu 16:

Nếu em là chủ cửa hàng kinh doanh mặt hàng giày da đang bán chạy trên thị trường thì em sẽ làm gì để hàng của mình bán được sản phẩm của mình.
Xem đáp án

Để hàng của mình bán được nhiều sản phẩm em sẽ:

− Nhờ bạn bè giúp đỡ, quảng cáo đến những người khác để họ biết đến và mua.

− Có kĩ năng ăn nói, giao tiếp tốt để được người khác yêu mến và ghé thăm cửa hàng nhiều hơn.

− Học hỏi một số cách kinh doanh tốt từ người khác, không sử dụng các thủ đoạn xấu để lấy lợi cho bản thân.

Câu 17:

Một khu đất hình chữ nhật có chu vi là 0,45 km. Chiều rộng bằng \(\frac{4}{5}\) chiều dài.

a, Tính diện tích khu đất đó với đơn vị đo là mét vuông.

b, Người ta dành \(\frac{3}{5}\) diện tích khu đất đó để làm trang trại. Hỏi diện tích đất còn lại là bao nhiêu mét vuông?
Xem đáp án

Đổi 0,45 km = 450 m

Nửa chu vi là

450 : 2 = 225 (m)

Chiều dài là

225 : (4 + 5) × 5 = 125 (m)

Chiều rộng là

225 – 125 = 100 (m)

Diện tích là

125 × 100 = 12500 (m2)

b)

Diện tích còn lại là

12500 – 12500 × \(\frac{3}{5}\) = 5000 (m2).

Câu 18:

11,25 km = ........m.
Xem đáp án

11,25 km = 11 250 m.

Câu 19:

So sánh: 2225 và 3151.
Xem đáp án

2225 = (23)75 = 875

3151 > 3150 = (32)75 = 975

⇒ 3151 > 975 > 875

⇒ 3151 > 2225.

Câu 20:

Cho tỉ lệ thức \(\frac{{3x - y}}{{x + y}} = \frac{3}{4}\). Hãy tính \(\frac{x}{y}\).
Xem đáp án

\(\frac{{3x - y}}{{x + y}} = \frac{3}{4}\)

⇒ 4(3x – y) = 3(x + y)

⇒ 12x – 4y = 3x + 3y

⇒ 9x = 7y

Vậy \(\frac{x}{y} = \frac{7}{9}\).

Câu 21:

Cho \(\frac{a}{b} = \frac{c}{d}\). Chứng minh \(\frac{{5a + 3b}}{{5a - 3b}} = \frac{{5c + 3d}}{{5c - 3d}}\).
Xem đáp án

\(\frac{a}{b} = \frac{c}{d} = x \Leftrightarrow a = bx;\,\,c = dx\)

Thay vào vế trái ta có:

\(\frac{{5a + 3b}}{{5a - 3b}} = \frac{{5bx + 3b}}{{5bx - 3b}} = \frac{{b(5x + 3)}}{{b(5x - 3)}} = \frac{{5x + 3}}{{5x - 3}}\) (1)

Thay vào vế phải ta có:

\(\frac{{5c + 3d}}{{5c - 3d}} = \frac{{5dx + 3d}}{{5dx - 3d}} = \frac{{d(5x + 3)}}{{d(5x - 3)}} = \frac{{5x + 3}}{{5x - 3}}\) (2)

Từ (1) và (2) ta có: \(\frac{{5a + 3b}}{{5a - 3b}} = \frac{{5c + 3d}}{{5c - 3d}}\).

Câu 22:

Cho tam giác ABC vuông tại A (AB < AC). Gọi E là trung điểm của BC. Từ E lần lượt kẻ ED vuông góc AC tại D, EF vuông góc với AB tại F.

a) Chứng minh tứ giác ADEF là hình chữ nhật.

b) Gọi K là điểm đối xứng của E qua F. Chứng minh tứ giác AEBK là hình thoi.
Xem đáp án
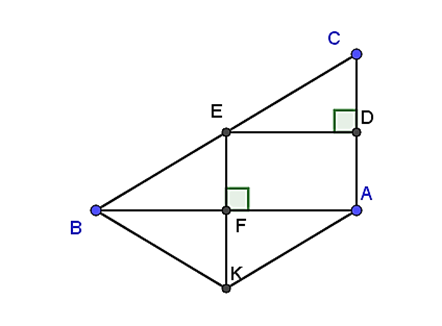
Cho tam giác ABC vuông tại A (AB < AC). Gọi E là trung điểm của BC. Từ E (ảnh 1)

a)

Xét tứ giác ADEF

\(\begin{array}{l}\widehat A = 90^\circ \\\widehat {ADE} = 90^\circ \\\widehat {EFA} = 90^\circ \end{array}\)

Do đó, ADEF là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật).

b)

Xét tam giác CBA có:

E là trung điểm của BC (gt)

EF song song với CA (do EF song song với AD, C thuộc DA)

Do đó, F là trung điểm của AB (định lý về đường trung bình của tam giác)

Xét tứ giác AEBF có

F là trung điểm của đường chéo AB(cmt)

F là trung điểm của đường chéo EK(do E và K đối xứng nhau qua F)

Do đó: AEBF là hình bình hành(dấu hiệu nhận biết hình bình hành)

mà EK vuông góc với AB (do EF vuông góc với AB, K thuộc EF)

nên AEBF là hình thoi(dấu hiệu nhận biết hình thoi).

Câu 23:

Khi viết thêm chữ số 2 vào bên trái của số có 5 chữ số thì số đó tăng thêm bao nhiêu đơn vị.

Xem đáp án

Khi viết thêm 1 chữ số 2 vào bên trái số có hai chữ số thì số đó tăng thêm 200 000 đơn vị.

Bắt đầu thi ngay

Bài thi liên quan