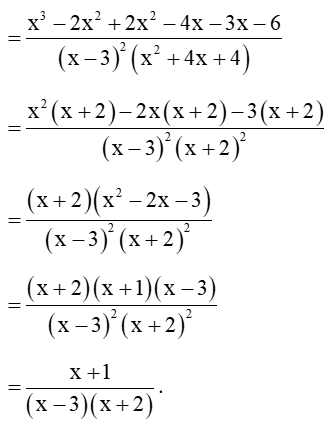- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 22)
-
12902 lượt thi
-
95 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC có , AC = 2 và . Hỏi bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Ta có .
Theo công thức Heron, ta có:
.
Bán kính đường tròn ngoại tiếp là:
.
Câu 2:
Tam giác ABC có . Gọi D là chân đường phân giác trong . Khi đó bằng bao nhiêu độ?
 Xem đáp án
Xem đáp án
Theo định lí hàm Cosin ta có:
•
.
•
.
Tam giác ABD có:
Câu 3:
Cho tam giác ABC vuông cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Các đường thẳng vuông góc kẻ từ A và E với CD cắt BC ở G và H. Đường thẳng EH và đường thẳng AB cắt nhau ở M. Đường thẳng kẻ từ A song song với BC cắt MH ở I. Chứng minh:
a) ∆ACD = ∆AME.
 Xem đáp án
Xem đáp án
a) Ta có:
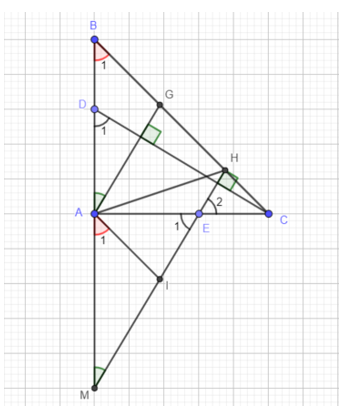
(hai góc đối đỉnh)
(Do cùng phụ với )
.
Xét ∆ACD và ∆AME có:
AD = AE (gt)
(cmt)
Þ ∆ACD = ∆AME (c.g.c).
Câu 4:
Chứng minh:
b) ∆AGB = ∆MIA.
 Xem đáp án
Xem đáp án
b) ∆ACD = ∆AME (câu a)
Þ AC = AM (hai cạnh tương ứng bằng nhau)
Mà AC = AB (Do ∆ABC vuông cân tại đỉnh A)
Þ AM = AB
Xét ∆AGB và ∆MIA có:
(AI // BC, hai góc ở vị trí đồng vị)
AB = MA (cmt)
(AG // MH do cùng ^ DC, hai góc ở vị trí đồng vị)
Þ ∆AGB = ∆MIA (g.c.g).
Câu 5:
Chứng minh:
c) BG = GH.
 Xem đáp án
Xem đáp án
c) ∆AGB = ∆MIA Þ BG = AI (1)
Xét ∆GAH và ∆IHA có:
(hai góc ở vị trí so le trong)
AH: cạnh chung
(hai góc ở vị trí so le trong)
Þ ∆GAH = ∆IHA (g.c.g)
Þ HG = AI (2)
Từ (1) và (2) suy ra BG = HG (đpcm).
Câu 6:
Cho tam giác ABC vuông cân ở A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Từ C kẻ đường thẳng vuông góc với BE cắt BA ở I a) Chứng minh: BE = CI.
 Xem đáp án
Xem đáp án
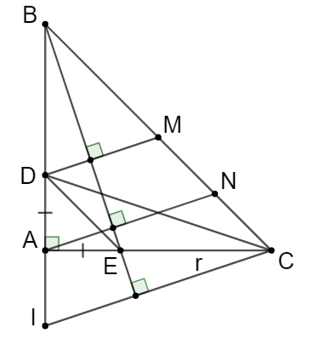
a) Ta có:
và (tổng 2 góc nhọn trong tam giác vuông)
.
∆ABC vuông cân tại A có AB = AC
Xét ∆ABE và ∆ACI có:
(cmt)
AB = AC (cmt)
Þ ∆ABE = ∆ACI (g.c.g)
Þ BE = CI (hai cạnh tương ứng bằng nhau).
b) Ta có:
Câu 7:
b) Qua D và A kẻ đường thẳng vuông góc với BE cắt BC lần lượt ở M và N. Chứng minh: MN = NC.
 Xem đáp án
Xem đáp án
b) Ta có:
AD = AE (gt)
AB = AC (cmt)
Do đó theo định lí Ta lét đảo, ta có:
DE // BC Þ Tứ giác DECB là hình thang.
Mà (∆ABC vuông cân tại A)
Þ Tứ giác DECB là hình thang cân
Þ CD = BE (2 đường chéo của hình thang cân).
Mà BE = CI nên CD = CI.
Xét ∆CAD và ∆CAI có:
CD = CI (cmt)
CA: cạnh chung
Þ ∆CAD = ∆CAI (cạnh huyền - cạnh góc vuông)
Þ AD = AI (hai cạnh tương ứng).
Mà AD + AI = DI nên .
Ta có:
• BE ^ DM và BE ^ AN Þ DM // AN
Theo định lí Ta lét ta có: (1)
• BE ^ DM và BE ^ CI Þ DM // CI
Theo định lí Ta lét ta có:
(2)
Từ (1) và (2)
Mà N Î MC nên N là trung điểm của MC
Þ MN = NC.
Câu 8:
Cho tam giác ABC có hb + hc = 2ha. Chứng minh rằng:
 Xem đáp án
Xem đáp án
Ta có hb + hc = 2ha
Áp dụng định lí sin ta có:
.
Vậy (đpcm).
Câu 9:
Trong tam giác ABC, nếu có 2ha = hb + hc thì:
 Xem đáp án
Xem đáp án
2ha = hb + hc
Áp dụng định lí sin ta có:
Vậy
Vậy nếu có 2ha = hb + hc thì:
Vậy ta chọn đáp án A.
Câu 10:
Cho tam giác ABC không có góc tù và: Tính góc A.
 Xem đáp án
Xem đáp án
Ta có:
(1)
Ta thấy:
Vì ∆ABC không tù nên 0 £ cos A < 1
(2)
Từ (1) và (2) thì đẳng thức xảy ra khi tất cả các dấu “=” ở trên xảy ra
Với
.
Câu 11:
Tam giác ABC không tù, thỏa mãn điều kiện
.
Tính ba góc của tam giác ABC.
 Xem đáp án
Xem đáp án
Ta có:
(1)
Ta thấy:
Vì ∆ABC không tù nên 0 £ cos A < 1
(2)
Từ (1) và (2) thì đẳng thức xảy ra khi tất cả các dấu “=” ở trên xảy ra
Vậy với thì .
Câu 12:
Cho phương trình x2 − 4x − m2 − 1 = 0. Tìm m để phương trình có hai nghiệm x1, x2 sao cho biểu thức x2 = −5x1.
 Xem đáp án
Xem đáp án
x2 − 4x − m2 − 1 = 0
Ta có ∆' = 4 + m2 + 1 = 5 + m2
Vì m2 ≥ 0 Þ m2 + 5 > 0; ∀m
Suy ra phương trình luôn có 2 nghiệm x1, x2
Theo định lí Viét, ta có:
Ta có: x2 = −5x1
Û 4 − x1 = −5x1
Û 4 = −4x1
Û x1 = −1
Þ x2 = (−5).(−1) = 5
Thay x1, x2 vào (*) ta được:
(−1).5 = − m2 − 1
Û − m2 − 1 = −5
Û m2 = 4 Û m = ±2
Vậy m = ±2 là giá trị của tham số m cần tìm.
Câu 13:
Cho phương trình x2 − 4x − m2 − 1 = 0.
a) Chứng minh phương trình luôn có 2 nghiệm phân biệt với mọi m.
 Xem đáp án
Xem đáp án
a) x2 − 4x − m2 − 1 = 0
Ta có ∆' = 4 + m2 + 1 = 5 + m2
Vì m2 ≥ 0 Þ m2 + 5 > 0; ∀m
Suy ra phương trình luôn có 2 nghiệm x1, x2.
Câu 14:
b) Tính giá trị của A = x12 + x22 biết 2x1 + 3x2 = 13.
 Xem đáp án
Xem đáp án
b) Theo Viét ta có:
Ta có: 2x1 + 3x2 = 13
Û 2x1 + 3(4 − x1) = 13
Û 2x1 + 12 − 3x1 = 13
Û −x1 − 1 = 0
Û x1 = −1
Þ x2 = 4 − (−1) = 5.
Khi đó A = x12 + x22 = (−1)2 + 52 = 26.
Câu 15:
Cho phương trình x2 + mx − 3 = 0. Tìm m để phương trình có hai nghiệm phân biệt x1, x2 thoả mãn |x1| + |x2| = 4.
 Xem đáp án
Xem đáp án
x2 + mx − 3 = 0
Þ ∆' = m2 + 12 > 0, ∀m Î ℝ nên phương trình luôn có hai nghiệm phân biệt với mọi m.
Áp dụng định lí Ta-lét, ta có:
Khi đó: |x1| + |x2| = 4
Û (|x1| + |x2|)2 = 16
Û x12 + x22 + 2|x1.x2| = 16
Û (x1 + x2)2 − 2x1.x2 + 2|x1.x2| = 16
Û (−m)2 − 2.(−3) +2.|−3| = 16
Û m2 = 4 Û m = ±2.
Vậy m = ±2 là giá trị của tham số m cần tìm.Câu 16:
Tìm m để phương trình x2 + mx + m − 2 = 0 có hai nghiệm x1, x2 thỏa mãn |x1 − x2| = 2.
 Xem đáp án
Xem đáp án
x2 + mx + m − 2 = 0
Þ ∆' = m2 − m + 2 , ∀m Î ℝ.
Nên phương trình luôn có hai nghiệm phân biệt với mọi m.
Áp dụng định lí Ta-lét, ta có:
Khi đó: |x1 − x2| = 2
Û |x1 − x2|2 = 4
Û x12 + x22 − 2x1.x2 = 4
Û (x1 + x2)2 − 2x1.x2 − 2x1.x2 = 4
Û (x1 + x2)2 − 4x1.x2 = 4
Û (−m)2 − 4.(m − 2) = 4
Û m2 − 4m + 8 − 4 = 0
Û m2 − 4m + 4 = 0
Û (m − 2)2 = 0 Û m = 2.
Vậy m = 2 là giá trị của tham số m cần tìm.
Câu 17:
Cho a, b là hai đường thẳng song song và cách nhau một khoảng 2 cm. Lấy điểm O trên a và vẽ đường tròn (O; 2 cm). Chứng minh đường tròn này tiếp xúc với đường thẳng b
 Xem đáp án
Xem đáp án
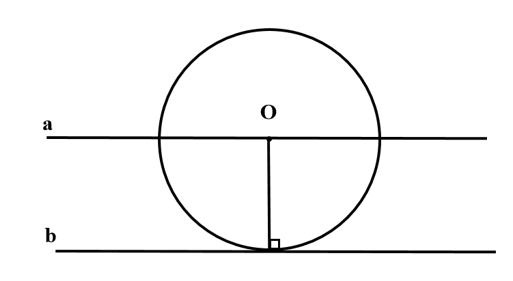
Vì tâm O của đường tròn (O; 2 cm) thuộc đường thẳng a và a // b.
Suy ra đường thẳng a cách đường thẳng b một khoảng 2 cm.
Do đó (O; 2 cm) tiếp xúc với b.
Câu 18:
Một bản đồ có tỉ lệ xích 1 : 1 000 000. Khoảng cách giữa hai địa điểm trên bản đồ là 5 cm. Tính khoảng cách giữa hai địa điểm đó trên thực tế (km).
 Xem đáp án
Xem đáp án
Ta có bản đồ tỉ lệ 1 : 1 000 000 và khoảng cách giữa địa điểm trên bản đồ là 5 cm.
Nên khoảng cách giữa hai địa điểm đó trên thực tế là:
(cm)
Đổi: 5 000 000 cm = 50 km.
Đáp số: 50 km.
Câu 19:
Trên bản đồ tỉ lệ 1 : 1 000 000, khoảng cách giữa hai thành phố A và B đo được 12,8 cm. Hỏi khoảng cách thức tế giữa hai thành phố là bao nhiêu ki-lô-mét?
 Xem đáp án
Xem đáp án
Ta có bản đồ tỉ lệ 1 : 1 000 000 và đo được khoảng cách giữa hai thành phố A và B là 12,8 cm.
Nên khoảng cách thực tế giữa hai thành phố A và B là:
(cm)
Ta có: 12 800 000 cm = 128 km
Đáp số: 128 km.
Câu 20:
Khi chia số tự nhiên a cho 36 ta được số dư là 12. Hỏi a có chia hết cho 4 không? Có chia hết cho 9 không?
 Xem đáp án
Xem đáp án
Ta có dư 12 nên a = 36k + 12
⇒ a = 4(9k + 3) nên a hoàn toàn chia hết cho 4.
Vì 4 không chia hết cho 9 và 9k + 3 chia cho 9 dư 3 hay không chia hết cho 9.
Vậy a không chia kết cho 9.
Câu 21:
Cho hình vuông ABCD. Gọi E là điểm đối xứng với A qua D.
a) Tam giác ACE vuông cân.
 Xem đáp án
Xem đáp án
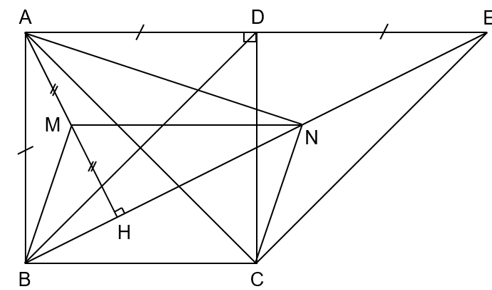
a) Ta có ABCD là hình vuông nên AB = BC = DC = AD và AC = BD (tính chất các cạnh và đường chéo của hình vuông).
Mà E đối xứng với A qua D nên DE = AD (gt)
⇒ DC = AD = DE.
⇒ ACE là tam giác vuông.
Mặc khác BC =AD = DE và BC // DE.
⇒ Tứ giác DECB là hình bình hành có BD = CE.
Mà BD = AC nền AC = CE
⇒ ACE là tam giác vuông cân.
Câu 22:
b) Kẻ AH vuông góc với BE. Gọi M, N theo thứ tự là trung điểm của AH và HE. Chứng minh tứ giác BMNC là hình bình hành.
 Xem đáp án
Xem đáp án
b) Theo đề ta có: MA = MH , NH = NE
⇒ MN là đường trung bình của ∆AHE
⇒ MN //AE và (1)
Ta có: AD = DE (gt) nên
Vì ABCD là hình vuông nên AD = BC và AD vuông góc với AB;
nên và DE // BC (2)
Từ (1) và (2) ⇒ MN = BC và MN//BC
⇒ Tứ giác BMNC là hình bình hành .
Câu 23:
c) Chứng minh M là trực tâm của tam giác ANB.
 Xem đáp án
Xem đáp án
c) Vì BMNC là hình bình hành (câu b) nên NM // BC
ABCD là hình vuông nên CB vuông góc AB
⇒ NM ⊥ AB (đl)
Xét Δ ANB có:
AH ⊥ BN (gt)
NM ⊥ AB(cmt)
AH ∩ NM tại M
⇒ M là trực tâm của ΔANB.
Câu 24:
So sánh A = 2 + 22 + 23 + 24 + ... + 22021 và B = 22022.
 Xem đáp án
Xem đáp án
Ta có: A = 2 +22+ 23 + 24 + ... + 22021
.
Câu 25:
Cho A = 2 + 22 + 23 + 24 +.....+ 260. Chứng minh rằng A chia hết cho 3.
 Xem đáp án
Xem đáp án
Ta có:
chia hết cho 3.
Câu 26:
Cho ba điểm A (1; −1), B (2; 1), C (−3; 1). Chứng minh đường thẳng AB vuông góc với đường thẳng AC.
 Xem đáp án
Xem đáp án
Gọi pt đường thẳng AB có dạng y = ax + b, do AB đi qua A và B nên:
⇒ y = 2x – 3
Gọi phương trình đường thẳng AC có dạng y = cx +d
Do tích 2 hệ số góc .
Vậy AB và AC vuông góc.
Câu 27:
Cho ba điểm A (1; 1); B (2; 0); C (3; 4). Viết phương trình đường thẳng đi qua A và cách đều hai điểm B, C.
 Xem đáp án
Xem đáp án
Gọi (d) là đường thẳng đi qua A và cách đều B, C. Khi đó ta có các trường hợp sau:
TH1: d đi qua trung điểm của BC.
là trung điểm của BC.
là vec tơ chỉ phương của đường thẳng d.
Khi đó (d): – 2(x – 1) + 3(y – 1) = 0 ⟺ 2x – 3y + 1 = 0.
TH2: d song song với BC, khi đó d nhận là vectơ chỉ phương.
Phương trình đường thẳng d là: – 4(x – 1) + y – 1 = 0 ⇔ 4x – y – 3 = 0.
Đáp án đúng là: A
Câu 29:
Tìm tập xác định D của hàm số .
 Xem đáp án
Xem đáp án
Hàm số xác định khi .
Vậy tập xác định của hàm số là .
Đáp án đúng là B.
Câu 30:
Cho hình bình hành ABCD trong đó có AD = 2AB. Kẻ CE vuông góc với AB. Gọi M là trung điểm của AD, nối EM, kẻ MF vuông góc với CE; MF cắt BC tại N.
a) Tứ giác MNCD là hình gì?
 Xem đáp án
Xem đáp án
a)
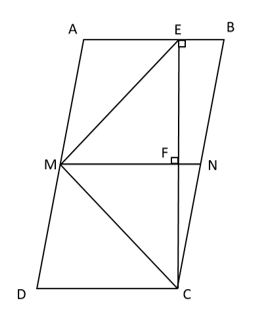
Theo đề ta có: CE vuông góc với AB và CE vuông góc với MN.
Suy ra AB // MN.
Mà ABCD là hình bình hành nên AB // CD.
Do đó MN // DC.
Mặc khác M là trung điểm của AD nên AD = 2MN;
Theo đề AD = 2AB = 2DC (vì ABCD là hình hình hành nên AB = DC).
Do đó MN = DC.
Xét tứ giác MNCD có:
MN // DC (cmt)
MN = DC
Suy ra MNCD là hình bình hành.
Câu 31:
 Xem đáp án
Xem đáp án
b) Ta có M là trung điểm của AD và MN // AB và MN // CD nên MN là đường trung bình của hình bình hành ABCD.
Suy ra BN = NC.
Xét ∆EBC có:
BN = NC; FN // EB.
⇒ FN là đường trung bình của tam giác EBC.
⇒ EF = FC.
Xét ∆EMC có MF vừa là đường cao vừa là đường trung tuyến
Do đó ∆MEC là tam giác cân tại M.
Câu 32:
c) Chứng minh rằng: .
 Xem đáp án
Xem đáp án
c) Ta có AB // MN nên .
Mà ∆MEC là tam giác cân tại M (câu b) nên MN là phân giác góc hay
.
Vì tứ giác MNCD là hình thoi nên MC là phân giác của
.
Mặc khác AB // MN nên .
(đpcm).
Câu 33:
Cho tam giác ABC có trung tuyến AM điểm K thuộc AC sao cho
a) Phân tích theo và .
 Xem đáp án
Xem đáp án
a)
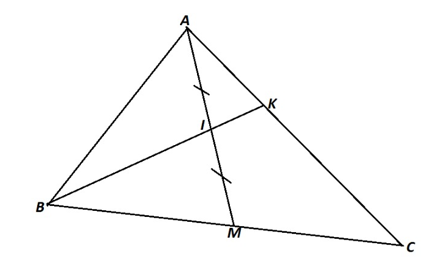
Ta có:
.
Câu 34:
 Xem đáp án
Xem đáp án
b) Vì I là trung điểm của AM nên:
Vậy B, I, K thẳng hàng.
Câu 35:
Cho hình chữ nhật ABCD đường chéo AC và BD cắt nhau tại O. Lấy P là điểm tùy ý trên OB. Gọi M là điểm đối xứng với C qua P. Từ M kẻ ME vuông góc với đường thẳng AB (F ∈ AB).
a) Chứng minh AEFM là hình chữ nhật.
 Xem đáp án
Xem đáp án
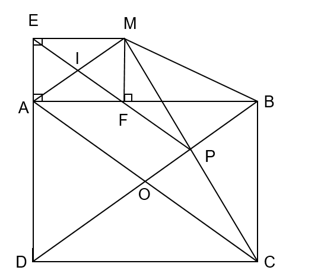
a) Ta có: (ABCD là hình vuông); (ME vuông góc AD tại E); (MF vuông góc AB tại F).
⇒Tứ giác AEMF có 3 góc vuông nên AEMF là hình chữ nhật.
Câu 36:
 Xem đáp án
Xem đáp án
b) Vì O là giao điểm hai đường chéo của hình chữ nhật ABCD (gt)
⇒ O là trung điểm AC
Mà P là trung điểm MC (gt)
⇒ OP là đường trung bình ∆AMC
Do đó OP // AM hay AM // BD.
Vậy AMBD là hình thang.
Câu 37:
c) Chứng minh E, F, P thẳng hàng.
 Xem đáp án
Xem đáp án
c) Ta có: AM // BD ⇒ .
Vì ABCD và AEMF cùng là hình chữ nhật (câu a) nên ta có:
;
;
.
Hai góc trên ở vị trí so le trong nên EF // AC (1)
Gọi I là giao điểm của EF và AM nên I là trung điểm của EF (AEMF là hình chữ nhật)
⇒ IP là đường trung bình ∆MAC nên IP // AC (2)
Từ (1) và (2) suy ra EF // IP hay E, I, F, P thẳng hàng.
Câu 38:
 Xem đáp án
Xem đáp án
d) Để từ giác AMBD là hình thang cân khi và chỉ khi AB = DM.
Mặc khác AB = DC nên DM = DC.
Vì P là trung điểm MC nên DP ⊥ MC.
Vậy CP ⊥ BD thì AMBD là hình thang cân.
Câu 39:
 Xem đáp án
Xem đáp án
Ta có: hb + hc = 2ha
Áp dụng định lý Sin trong tam giác ABC:
; (R: bán kính đường tròn ngoại tiếp tam giác)
.
Vậy .
Câu 40:
Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua C vuông góc với BD cắt Ab ở F. Chứng minh rằng D, E, F thẳng hàng.
 Xem đáp án
Xem đáp án
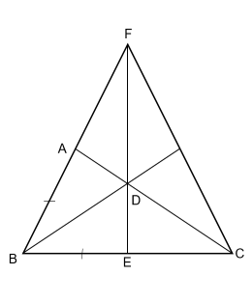
Xét ΔABD và ΔEBD có:
AB = BE (gt);
(BD là tia phân giác )
BD cạnh chung
⇒∆ABD = ∆EBD (c.g.c)
Mà (gt)
Suy ra: DE vuông BC
Mặc khác ∆FBC có CA, BD là đường cao cắt nhau tại D.
⇒ D là trực tâm của ∆FBC có DF ⊥ BC.
Ta có DE ⊥ BC; DF ⊥ BC.
Do đó hai đường thẳng DE, DF trùng nhau.
Vậy ba điểm D, E, F thẳng hàng.
Câu 41:
Cho tam giác ABC. Biết AB = 40 cm, AC = 58 cm, BC = 42 cm.
a) Tam giác ABC là tam giác gì? Tại sao?
 Xem đáp án
Xem đáp án
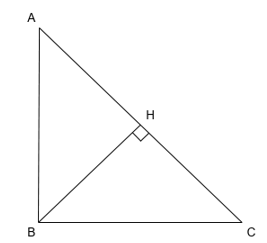
a) Theo đề ta có:
AB2 + BC2 = 402 + 422 = 3364
Mà AC2 = 582 = 3364
Suy ra, AC2 = AB2 + BC2
Vậy ∆ABC vuông tại B (theo định lí Py-ta-go đảo).
Câu 42:
b) Kẻ đường cao BH của tam giác ABC. Tính BH.
 Xem đáp án
Xem đáp án
b) Áp dụng hệ thức lượng trong ∆ABC vuông tại B (câu a), đường cao BH có:
BH.AC = AB. BC
(cm).
Vậy cm.
Câu 43:
 Xem đáp án
Xem đáp án
c) Trong ∆ABC vuông tại B có tỉ số lượng giác của góc A là:
;
;
;
.
Vì ∆ABC vuông tại B nên nên tỉ số lượng giác góc C là:
;
;
;
.
Câu 44:
Cho tam giác ABC có đường cao BH, AB = 40 cm, AC = 58 cm, BC = 42 cm.
a) Tam giác ABC có phải tam giác vuông không ? Vì sao?
 Xem đáp án
Xem đáp án
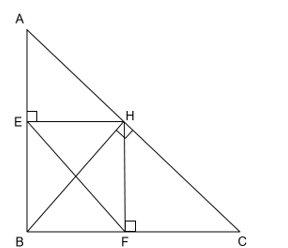
a) Tam giác ABC là tam giác vuông tại B vì:
AB2 + BC2 = 402 + 422 = 3364
Mà AC2 = 582 = 3364
Suy ra, AC2 = AB2 + BC2 (Định lý Py-ta-go đảo).
Câu 45:
 Xem đáp án
Xem đáp án
b) Trong ∆ABC vuông tại B có tỉ số lượng giác của góc A là:
;
;
;
;
Câu 46:
 Xem đáp án
Xem đáp án
c) Áp dụng hệ thức lượng trong ∆ABC vuông tại B (câu a), đường cao BH có:
BH.AC = AB. BC
(cm)
Vậy cm.
Áp dụng hệ thức lượng trong ∆BHA vuông tại H, có đường cao HE (giả thiết) có:
BH2 = BE.AB
(cm).
Tương tự:
Áp dụng hệ thức lượng trong ∆BHC vuông tại H, có đường cao HF (giả thiết) có:
BH2 = BF.AB
(cm)
Diện tích ∆ABC vuông tại B là:
(cm2)
Diện tích ∆BEF vuông tại B là:
(cm2).
Diện tích tứ giác EFCA là:
(cm2).
Câu 47:
Định nghĩa hình chiếu là gì?
 Xem đáp án
Xem đáp án
Hình chiếu là hình biểu diễn một mặt nhìn thấy của vật thể đối với người quan sát đứng trước vật thể, phần khuất được thể hiện bằng nét đứt.
Câu 48:
Số liền trước của số tròn chục lớn nhất có 6 chữ số khác nhau là?
 Xem đáp án
Xem đáp án
Số tròn chục lớn nhất có 6 chữ số khác nhau là số 987650.
Vậy số liền trước của số tròn chục lớn nhất có 6 chữ số khác nhau là số 987649.
Câu 49:
Gọi d là đường thẳng đi qua A(1;0) và có hệ số góc m. Tìm tất cả giá trị thực của tham số m để d cắt đồ thị hàm số (C) tại hai điểm phân biệt thuộc hai nhánh của đồ thị?
 Xem đáp án
Xem đáp án
Đường thẳng d có dạng y = m(x – 1) = mx – m.
Phương trình hoành độ giao điểm:
với (x ≠ 1)
⇔ x + 2 = (mx – m)(x – 1)
⇔ mx2 – (2m + 1)x + m – 2 = 0 (1)
Để d cắt (C) tại hai điểm phân biệt thuộc hai nhánh của đồ thị ⇔ phương trình (1) có hai nghiệm phân biệt x1 < x2 thỏa mãn x1 < 1 < x2 hay (x1 – 1)(x2 – 1) < 0
⇔ m > 0
Vậy m > 0.
Câu 50:
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A (2; 4), B (5; 1), C(– 1; – 2). Phép tịnh tiến theo véc tơ biến tam giác ABC thành tam giác A'B'C'. Tìm tọa độ trọng tâm của tam giác A'B'C'.
 Xem đáp án
Xem đáp án
Tọa độ vectơ = (–1 – 5; – 2 – 1) = ( – 6; – 3);
Gọi G (x1; y1) là trọng tâm tam giác ABC.
⇒ Tọa độ trong tâm tam giác ABC là G (2; 1).
Gọi G’ (x2; y2) là trọng tâm tam giác A'B'C'.
Phép tịnh tiến theo véc tơ biến tam giác ABC thành tam giác A'B'C' nên G(2; 1) cũng tịnh tiến theo véc tơ thành G’ (x2; y2).
Ta có: = = ( – 6; – 3)
.
Vậy G’ (– 4; – 2).
Câu 51:
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A (1; 4); B (4; 0); C (−2; −2). Phép tịnh tiến biến ∆ABC thành ∆A’B’C’. Tọa độ trực tâm của ∆A’B’C’ là: biến ∆ABC thành ∆A’B’C’. Tọa độ trực tâm của ∆A’B’C’ là:
 Xem đáp án
Xem đáp án
Ta có: Tọa độ véc tơ = (–2 – 4; – 2 – 0) = ( – 6; – 2);
(A) = A’ (−5; 2);
(B) = B’ ≡ C (−2 ;– 2);
(C) = C’ (−8 ;– 4);
Gọi H (x; y) là trực tâm tam giác A’B’C’, khi đó ta có HA’ ⊥ B’C’; HB’ ⊥ A’C’; HA’⊥ B’C’; HB’ ⊥ A’C’.
;
;
;
;
Vậy H (– 4; – 1).
Đáp án đúng là A.
Câu 52:
Một lớp học có 25 học sinh nam và 15 học sinh nữ. Tính tỉ số phần trăm của học sinh nữ so với học sinh nam.
 Xem đáp án
Xem đáp án
Tỉ số phần trăm của học sinh nữ so với học sinh nam là :
15 : 25 × 100 = 60 %
Đáp số: 60%.
Câu 53:
Một tổ có 25 học sinh nam, 15 học sinh nữ. Hỏi có bao nhiêu cách chọn 1 em làm lớp trưởng?
 Xem đáp án
Xem đáp án
Tổng số học sinh của tổ là: 25 + 15 = 40 (học sinh);
Vậy số cách để chọn ngẫu nhiên 1 em làm lớp trưởng là 40 cách.
Câu 54:
Cho góc nhọn . Trên tia Ox lấy hai điểm A và C, trên tia Oy lấy hai điểm B và D, sao cho OA = OD, OC = OD (A nằm giữa O và C, B nằm giữa C và D). Chứng minh:
a) ∆OAD = ∆OBC.
 Xem đáp án
Xem đáp án
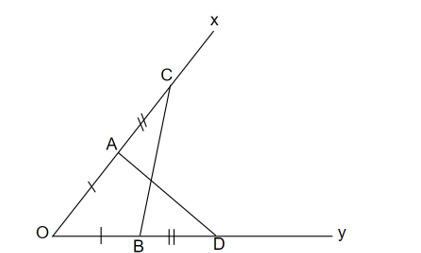
a) Xét ∆OAD và ∆OBC có:
OA = OB (gt)
Góc chung (gt)
OC = OD (gt)
Vậy ∆OAD = ∆OBC (c.g.c).
Câu 55:
b) So sánh và .
 Xem đáp án
Xem đáp án
b) Ta có: ∆OAD = ∆OBC (câu a)
(hai góc tương ứng)
Mặc khác: (hai góc kề bù)
(hai góc kề bù)
.
Câu 56:
Một căn phòng hình chữ nhật có chiều dài 12 m, chiều rộng bằng chiều dài. Để lát nền căn phòng đó, người ta dùng loại gạch men hình có có cạnh 8 dm. Hỏi căn phòng đó được lát bao nhiêu viên gạch men đó? (Phần diện tích mạch vữa không đáng kể).
 Xem đáp án
Xem đáp án
Chiều dài của căn phòng :
(m) = 40 (dm)
Ta có: 12 m = 120 dm
Diện tích của căn phòng :
120 × 40 = 4 800 (dm2)
Diện tích mỗi viên gạch men :
8 × 8 = 16 (dm2)
Số viên gạch men dùng để lát căn phòng là
4800 : 16 = 300 (viên gạch men)
Đáp số: 300 viên gạch men
Câu 57:
Một căn phòng hình chữ nhật có chiều dài hơn chiều rộng 4 m chiều rộng bằng chiều dài. Người ta lát nền căn phòng bằng gạch men hình vuông có cạnh 2 dm. Hỏi cần bao nhiêu viên gạch men để lát kín phòng đó? (không tính mạch vữa)
 Xem đáp án
Xem đáp án
4 m = 40 dm
Chiều rộng căn phòng là :
40 : ( 4 − 3) × 3 = 120 (dm)
Chiều dài căn phòng là :
40 : ( 4 − 3 ) × 4 = 160 (dm)
Diện tích căn phòng là :
120 × 160 = 19200 (dm2)
Diện tích viên gạch là :
2 × 2 = 4 (dm2)
Cần số gạch để lát căn phòng là :
19200 : 4 = 4800 (viên gạch)
Đáp số: 4800 viên gạch.
Câu 58:
 Xem đáp án
Xem đáp án
Điều kiện xác định của biểu thức: 2 ≤ x ≤ 4.
Ta có: (với a, b ≥ 0).
Nên
Do đó GTLN của biểu thức là 2.
Ta có:
Dấu “=” xảy ra khi a = 0 hoặc b = 0;
Áp dụng vào biểu thức:
Đẳng thức xảy ra .
GTNN của biểu thức là: với x = 2 hoặc x = 4.
Câu 59:
Tìm x biết: (x – 5)(x – 4) – (x + 1)(x – 2) = 7
 Xem đáp án
Xem đáp án
(x – 5)(x – 4) – (x + 1)(x – 2) = 7
⇔ x2 – 4x – 5x + 20 – (x2 – 2x + x – 2) = 7
⇔ x2 – 4x – 5x + 20 – x2 + 2x – x + 2 = 7
⇔ – 8x + 22 = 7
⇔ – 8x = 7 – 22
⇔ – 8x = – 15
Vậy .
Câu 60:
 Xem đáp án
Xem đáp án
A = n3 + (n + 1)3 + (n + 2)3
= n3 + n3 + 3n2 + 3n + 1 + n3 + 6n2 + 12n + 8
= 3n3 + 9n2 + 15n + 9
= 3n2 (n + 1) + 6n ( n + 1) + 9 (n +1)
= 3 (n + 1)(n2 + 2n + 3)
=3(n + 1)[n (n + 2) + 3]
= 3n (n + 1)(n + 2) + 9( n + 1)
Ta có: n; n + 1; n + 2 là 3 số tự nhiên liên tiếp
⇒ 3n(n + 1)(n + 2) ⋮ 9
Mặc khác: 9(n + 1) ⋮ 9
⇒ A = 3n (n + 1)(n + 2) + 9(n + 1) ⋮ 9.
Vậy A = n3 + (n + 1)3 + (n + 2)3 ⋮ 9.
Câu 61:
Một chiếc thùng không cân nặng 8,7 kg, mỗi lít dầu cân nặng 0,95 kg. Hỏi thùng đó đựng 25 lít dầu cân nặng bao nhiêu kg?
 Xem đáp án
Xem đáp án
Số cân nặng của 25 lít dầu là:
25 × 0,95 = 23,75 (kg)
Tổng số cân nặng của thùng đựng 25 lít dầu là:
23,75 + 8,7 = 32,45 (kg).
Đáp số: 32,45 kg.
Câu 62:
Thị trấn A cách thị trấn B là 20 km theo đường thẳng. Một người đi xe đạp rời thị trấn A và đi đến thị trấn B với tốc độ 20 km/h. Vào đúng thời điểm đó, người đi xe đạp thứ hai rời thị trấn B đi đến thị trấn A với tốc độ 15 km/h.
a) Hai người đi xe đạp sẽ gặp nhau ở đâu giữa hai thị trấn?
 Xem đáp án
Xem đáp án
a) Gọi s (km) là khoảng cách từ thị trấn A đến điểm gặp nhau.
Thời gian chuyển động của hai người là như nhau (do xuất phát cùng lúc) nên:
Từ đây ta có s = 11,4 km.
Vậy hai người đi xe đạp sẽ gặp nhau ở vị trí cách thị trấn A là 11,4 km.
Câu 63:
b) Khoảng thời gian từ lúc xuất phát đến khi họ gặp nhau (tính bằng phút)?
 Xem đáp án
Xem đáp án
b) Thời gian từ lúc xuất phát đến lúc gặp nhau:
(giờ) = 34,2 (phút).
Vậy khoảng thời gian từ lúc xuất phát đến khi họ gặp nhau là 34,2 phút.
Câu 64:
Tìm m để y = 2x3 − mx2 + 2x đồng biến trên (−2; 0).
 Xem đáp án
Xem đáp án
Ta có:
(1)
Đề hàm số đồng biến trên (− 2; 0)
với
Xét
.
Vậy .
Câu 66:
Chứng minh rằng: a4 + b4 + c4 ≥ abc(a + b + c).
 Xem đáp án
Xem đáp án
Áp dụng bất đẳng thức:
a2 + b2 + c2 ≥ ab + ac + bc
⇒ a4 + b4 + c4 ≥ a2b2 + a2c2 + b2c2
Mà: a2b2 + a2c2 + b2c2 ≥ a2bc + ab2c + abc2
Mặc khác: a2bc + ab2c + abc2 = abc(a + b + c).
Vậy: a4 + b4 + c4 ≥ abc(a + b + c).
Câu 67:
Cho đường tròn (O; R), đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến (d) và (d’) với đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở M và cắt đường thẳng (d’) ở P. Từ O vẽ một tia vuông góc với MP và cắt (d’) ở N.
a) Chứng minh OM = OP và ∆NMP cân.
 Xem đáp án
Xem đáp án
a)
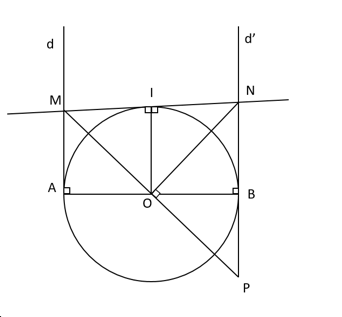
Xét ∆AMO và ∆BPO có:
OA = OB = R
(đối đỉnh)
⇒ ∆AMO = ∆BPO (gcg)
⇒ OM = OP ⇒ O là trung điểm MP.
Xét ∆MNP có NO vừa là đường cao vừa là đường trung tuyến
⇒ ∆MNP cân tại N.
Câu 68:
b) Kẻ OI vuông góc MN (I ∈ MN). Chứng minh OI = R và MN là tiếp tuyến của đường tròn (O).
 Xem đáp án
Xem đáp án
b) Ta có: ∆MNP cân tại N (câu a)
⇒ ON là đường phân giác hay
Xét ∆INO và ∆BNO có:
ON là cạnh chung;
(cmt)
Do đó ∆INO = ∆BNO (g.c.g)
Suy ra OI = OB = R.
Câu 69:
c) Chứng minh : AM.BN = R2.
 Xem đáp án
Xem đáp án
c) ∆INO = ∆BNO (câu b)
⇒ NI = NB (1)
Xét ∆OIM và ∆OAM có:
OM là cạnh chung
OI = OA = R
⇒ ∆OIM = ∆OAM (cgc)
⇒MA = MI (2)
Từ (1) và (2) ⇒ MA . NB = MI . NI
Xét ∆MON vuông tại O có OI là đường cao:
OI2 = MI.NI = R2 ⇒ MA. MB = R2.
Câu 70:
d) Tìm vị trí của M để diện tích tứ giác AMNB nhỏ nhất.
 Xem đáp án
Xem đáp án
d) Xét tứ giác AMNB có
⇒ AMNB là hình thang vuông
.
Mà
Mà
⇒ S AMNB ≥ 2R2.
Dấu = xảy ra khi MI = NI hay I là trung điểm MN
⇒ AM = R.
Vậy M thuộc (d) và cách A một khoảng bằng R thì SAMNB = 2R2.
Câu 71:
Cho hình chữ nhật ABCD vẽ tam giá AEC vuông tại E. Chứng minh năm điểm A, B, C, D, cùng thuộc một đường tròn.
 Xem đáp án
Xem đáp án
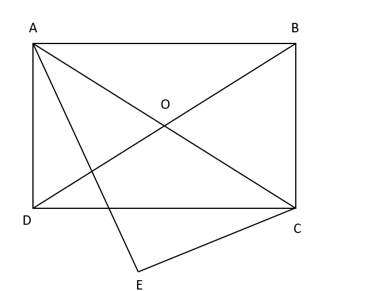
Vì ABCD là hình chữ nhật nên nội tiếp đường tròn .
Xét tứ giác ADEC có
Do đó tứ giác ADEC nội tiếp
Vậy 5 điểm A, B, C, D, E cung thuộc đường tròn .
Câu 72:
Tìm giá trị nhỏ nhất:
a) A = x2 + 4y2 – 4x + 32y + 2078;
 Xem đáp án
Xem đáp án
a) Ta có A = x2 + 4y2 – 4x + 32y + 2078
= (x2 – 4x +2) + (4y2 + 32y + 64) + 2010
= (x – 2)2 + (2y + 8)2 + 2010
Vì (x – 2)2 ≥ 0; (2y + 8)2 ≥ 0 nên A = (x – 2)2 + (2y + 8)2 + 2010 ≥ 2010.
Dấu = xảy ra khi x – 2 = 0 và 2y + 8 = 0.
Vây Amin = 2010 ⇔ (x; y) = (2; – 4).
Câu 73:
Tìm giá trị nhỏ nhất:
b) B = 3x2 + y2 + 4x – y .
 Xem đáp án
Xem đáp án
b) Ta có: B = 3x2 + y2 + 4x – y
.
Dấu = xảy ra khi ; .
Vậy .
Câu 74:
Bạn An làm một phép chia có số dư là số dư lớn nhất, có thể có sau đó An giảm cả số bị chia và số chia đi 5 lần ở phép chia mới này, thương số là 75, số dư là 4. Tìm phép chia ban đầu.
 Xem đáp án
Xem đáp án
Ở phép chia lần thứ hai khi cùng giảm cả số bị chia và số chia đi 5 thì thương số là 75 số dư là 4 nên thương và số dư không thay đổi.
Suy ra ở phép chia lần thức nhất thương ban đầu vẫn là 75 và số dư ban đầu là 4.
Vì số dư lớn nhất là 4 nên số bị chia là 5.
Số chia ban đầu là: 75 × 5 + 4 = 379.
Vậy phép chia ban đầu là 379 : 5 = 75 dư 4.
Câu 75:
Bạn An làm một phép chia có số dư là số dư lớn nhất có thể có. Sau đó, An giảm ở cả số bị chia và số chia đi 2 lần. Ở phép chia mới có số thương là 162, số dư là 10. Tìm phép chia ban đầu.
 Xem đáp án
Xem đáp án
Ở phép chia mới khi cùng giảm cả số bị chia và số chia đi 2 thì thương số là 162 số dư là 10 nên thương và số dư không thay đổi.
Suy ra ở phép chia lần thức nhất thương ban đầu vẫn là 162 và số dư ban đầu là 10.
Vì số dư lớn nhất là 10 nên số bị chia là 11.
Số chia ban đầu là: 162 × 11 + 10 = 1792.
Vậy phép chia ban đầu là 1792 : 11 = 162 dư 10.
Câu 76:
25% của số đó là 40. Số đó là số nào?
 Xem đáp án
Xem đáp án
Vì 25% của số đó là 40.
Vậy số đã cho là: 40 : 25% = 160.
Đáp số: 160.
Câu 77:
Biết 25% của 1 số là 40. Tính số đó.
 Xem đáp án
Xem đáp án
Vì 25% của số là 40 nên giá trị của số đó là: 40 : 25% = 160
Giá trị của số đó là: .
Đáp số: 32.
Câu 78:
Cho a là số thực dương. Tìm tất cả các giá trị của a để hàm số f(x) xác định trên khoảng (−1; 1).
 Xem đáp án
Xem đáp án
Điều kiện xác định của hàm số :
Vậy để hàm số xác định trên khoảng (−1;1) .
Câu 79:
Cho hàm số f(x) xác định trên . Trong các khẳng định sau, khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Đáp án D đúng vì : hàm số y = f(x) liên tục tăng trên đoạn nên f(a) < f(x) < f(b) ∀x ∈ (a; b).
Ta có: f(a).f(b) > 0
Vậy f(x) = 0 không thể có nghiệm trong (a; b).
Câu 80:
Trong hệ trục tọa độ Oxy cho ba điểm A (1; −4), B (4; 5) và C (0; −9). Điểm M di chuyển trên trục Ox. Đặt . Biết giá trị nhỏ nhất của Q có dạng , trong đó a,b là các số nguyên dương a, b < 20. Tính a – b.
 Xem đáp án
Xem đáp án
Gọi M (m; 0) di chuyển trên trục Ox.
.
Vậy a – b = 6 – 17 = – 11.
Câu 82:
Cho đường thẳng (d): và điểm A (2; 5; 3).
a) Tìm tọa độ hình chiếu vuông góc H của A trên đường thẳng (d).
 Xem đáp án
Xem đáp án
a) Véc tơ chỉ phương của đường thẳng d là: ;
Vì H là hình chiếu của A trên đường thẳng d nên H ∈ (d)
Vậy H (3; 1; 4).
Câu 83:
b) Viết phương trình mặt phẳng (P) chứa đường thẳng (d) sao cho khoảng các từ A đến (P) đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
b) Gọi K là hình chiếu vuông góc của A trên (P). Ta có d(A; (P)) = AK ≤ AH
⇒K ≡ H ⇒ K (3;1;4).
Mặt phẳng (P) đi qua K (3;1;4) có véc tơ pháp tuyến là .
Vậy phương trình của mặt phẳng (P) là: x – 4y + z – 3 = 0.
Câu 84:
Cho đường tròn (O;R), và điểm A nằm ngoài đường tròn (O) sao cho OA = 2R.Vẽ tiếp tuyến AB với đường tròn (O). Gọi BH là đường cao của Δ ABO, BH cắt đường tròn (O) tại C.
a) Chứng minh: AC là tiếp tuyến của đường tròn (O).
 Xem đáp án
Xem đáp án
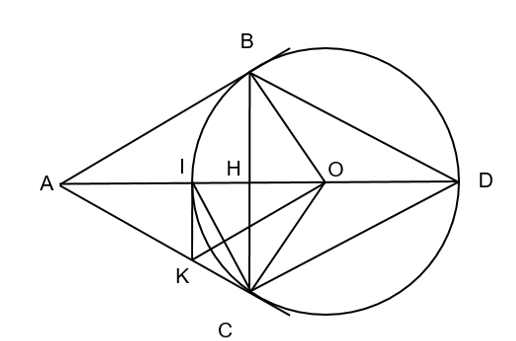
a) Xét ∆OBC có OB = OC = R
Suy ra ∆OBC cân tại O có OH là đường cao nên OH cũng là phân giác.
Do đó .
Xét ∆BAO và ∆CAO có:
OB = OC = R
(cmt)
OA là cạnh chung
Do đó ∆BAO = ∆CAO (c.g.c)
hay OC vuông góc với AC tại C.
Vậy AC là tiếp tuyến của (O).
Câu 85:
b) Từ O vẽ đường thẳng vuông góc với OB cắt AC tại K. Chứng minh: KA = KO.
 Xem đáp án
Xem đáp án
b) M là giao điểm của OK và BC.
Xét ∆BMO vuông tại O có OH vuông góc BM
.
Tương tự xét ∆ABO vuông tại B có BH vuông góc AO
Mà
⇒ ∆AKO cân tại K ⇒ AK = KO.
Câu 86:
Khi đo chiều dài của chiếc bàn học, một học sinh viết được kết quả: C = 118 ± 2 (cm). Sai số tỉ đối phép đo đó bằng
 Xem đáp án
Xem đáp án
Sai số tỉ đối của phép đo đó là: .
Đáp án đúng là B.
Câu 87:
Khi đo chiều dài của chiếc bàn học, một học sinh viết được kết quả: l = 158 ± 2 (cm). Sai số tương đối của phép đo đó bằng
 Xem đáp án
Xem đáp án
Sai số tương đối của phép đo đó là: .
Đáp án đúng là D.
Câu 88:
Tìm số tự nhiên a nhỏ nhất có ba chữ số. Biết rằng a chia cho 11 dư 3 và a chia cho 13 dư 5.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là a thì a + 8 ∈ BC (11; 13) và a là số nhỏ nhất thỏa mãn 100 ≤ a ≤ 999.
Ta có BCNN (11; 13) = 11.13 = 143.
BC (11;13) ∈ {0; 143; 286; ...}.
Vì a là số tự nhiên có ba chữ số nhỏ nhất nên a + 8 = 143 ⇒ a = 135.
Vậy số cần tìm là 135.
Câu 89:
2. Mặt phẳng (CMN) chia khối chóp đã cho thành hai phần, thể tích của phần có thể tích nhỏ hơn bằng:
 Xem đáp án
Xem đáp án
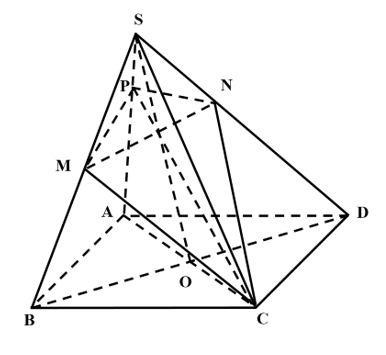
Ta có: ; ;
; ;
Mà:
.
Câu 90:
Cho 2 đường thẳng (d): y = – x + m + 2 và (d'): y= (m2 – 2).x + 1.
a) Khi m = – 2, hãy tìm tọa độ giao điểm của hai đường thẳng.
 Xem đáp án
Xem đáp án
a) m = – 2 thì (d): y = − x; (d'): y = 2x + 1.
Gọi M (x0; y0) là giao điểm của 2 đường thẳng (d) và (d')
⇒ (d): y0 = – x0 ; (d'): y0 = 2x0 + 1
.
Vậy tọa độ giao điểm của 2 đường thẳng trên là: .Câu 91:
b) Tìm m để (d) song song với (d').
 Xem đáp án
Xem đáp án
b) Điều kiện để (d) song song với (d'):
Vậy m = 1 thì (d) song song với (d').
Câu 92:
Tam giác ABC vuông tại A có AB = 6 cm; AC = 8 cm và BC = 10 cm. Đường cao AH dài là:
 Xem đáp án
Xem đáp án
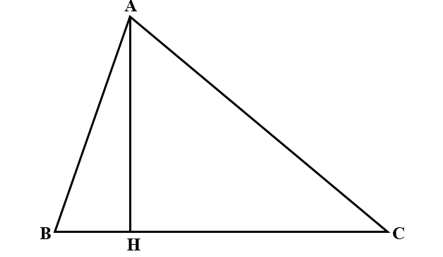
Độ dài đường cao AH của tam giác ABC vuông tại A là:
(cm).
Đáp án đúng là A.
Câu 93:
Chuẩn bị chào mừng ngày nhà giáo Việt Nam 20/11, đội văn nghệ trường THPT X gồm 9 học sinh, trong đó 3 học sinh nữ chia thành 3 tổ đều nhau (mỗi tổ 3 học sinh) để làm công tác biểu diễn văn nghệ. Tính xác xuất để mỗi tổ có đúng 1 nữ.
 Xem đáp án
Xem đáp án
Số các chọn 3 học sinh vào mỗi tổ: .
Chia 3 bạn nữ vào 3 tổ: 3! = 6
Xếp 6 bạn nam vào 3 tổ: .
Xác suất: .
Câu 94:
Tính chu vi và diện tích hình thang cân ABCD biết 2 cạnh đáy AB = 12 cm, CD = 18 cm, .
 Xem đáp án
Xem đáp án
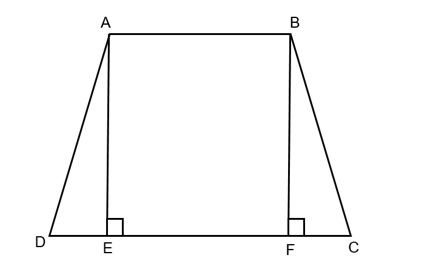
Từ A kẻ AE vuông góc với DC tại E;
Từ B kẻ BF vuông góc với DC tại E;
⇒ AE // BF
Xét tứ giá ABFE có: AB // EF (ABCD là hình thang cân) ; AE //BF (cmt) và
⇒ ABFE là hình chữ nhật
Xét ∆ADE và ∆BFC có:
AD = BC và (do ABCD là hình thang cân)
⇒ ∆ADE = ∆BFC (cạnh huyền – góc nhọn)
(cm)
Xét ∆ADE vuông tại E có:
(cm)
(cm)
Chu vi hình thang cân ABCD là: 12 + 18 + 11,6.2 = 53,2 (cm)
Diện tích hình thang cân ABCD là: (cm2).
Câu 95:
Cho hình thang ABCD diện tích hình thang là 225 cm2, đáy nhỏ AB = 12 cm đáy lớn CD = 18 cm. Tính diện tích tam giác ABC và tam giác ACD.
 Xem đáp án
Xem đáp án
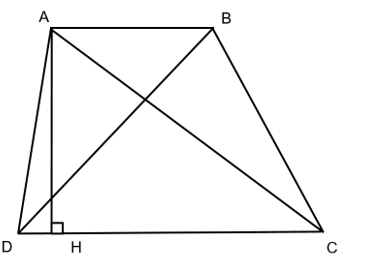
Chiều cao hình thang ABCD là: 225.2 : ( 12 + 18 ) = 15 (cm)
Ta có: Chiều cao của hình thang ABCD chính là chiều cao của hình tam giác ACD và độ dài đáy của hình tam giác ACD bằng 18 cm.
Diện tích hình tam giác ACD là : 15.18 : 2 = 135 (m2).
Diện tích hình tam giác ABC là : 225 − 135 = 90 (m2).