Cho đường tròn (O; R), đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến (d) và (d’) với đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở M và cắt đường thẳng (d’) ở P. Từ O vẽ một tia vuông góc với MP và cắt (d’) ở N.
a) Chứng minh OM = OP và ∆NMP cân.
 Giải bởi Vietjack
Giải bởi Vietjack
a)
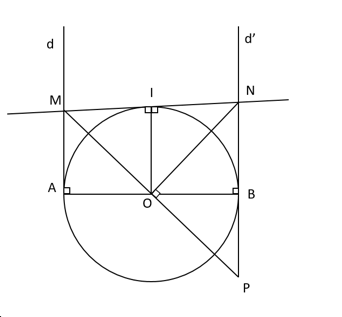
Xét ∆AMO và ∆BPO có:
OA = OB = R
(đối đỉnh)
⇒ ∆AMO = ∆BPO (gcg)
⇒ OM = OP ⇒ O là trung điểm MP.
Xét ∆MNP có NO vừa là đường cao vừa là đường trung tuyến
⇒ ∆MNP cân tại N.
Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua C vuông góc với BD cắt Ab ở F. Chứng minh rằng D, E, F thẳng hàng.
Cho ba điểm A (1; 1); B (2; 0); C (3; 4). Viết phương trình đường thẳng đi qua A và cách đều hai điểm B, C.
Cho tam giác ABC vuông cân ở A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Từ C kẻ đường thẳng vuông góc với BE cắt BA ở I a) Chứng minh: BE = CI.
Cho đường tròn (O;R), và điểm A nằm ngoài đường tròn (O) sao cho OA = 2R.Vẽ tiếp tuyến AB với đường tròn (O). Gọi BH là đường cao của Δ ABO, BH cắt đường tròn (O) tại C.
a) Chứng minh: AC là tiếp tuyến của đường tròn (O).
Cho hình bình hành ABCD trong đó có AD = 2AB. Kẻ CE vuông góc với AB. Gọi M là trung điểm của AD, nối EM, kẻ MF vuông góc với CE; MF cắt BC tại N.
a) Tứ giác MNCD là hình gì?
Cho tam giác ABC có , AC = 2 và . Hỏi bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?
Thị trấn A cách thị trấn B là 20 km theo đường thẳng. Một người đi xe đạp rời thị trấn A và đi đến thị trấn B với tốc độ 20 km/h. Vào đúng thời điểm đó, người đi xe đạp thứ hai rời thị trấn B đi đến thị trấn A với tốc độ 15 km/h.
a) Hai người đi xe đạp sẽ gặp nhau ở đâu giữa hai thị trấn?
Cho tam giác ABC vuông cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Các đường thẳng vuông góc kẻ từ A và E với CD cắt BC ở G và H. Đường thẳng EH và đường thẳng AB cắt nhau ở M. Đường thẳng kẻ từ A song song với BC cắt MH ở I. Chứng minh:
a) ∆ACD = ∆AME.
Cho góc nhọn . Trên tia Ox lấy hai điểm A và C, trên tia Oy lấy hai điểm B và D, sao cho OA = OD, OC = OD (A nằm giữa O và C, B nằm giữa C và D). Chứng minh:
a) ∆OAD = ∆OBC.
Trong hệ trục tọa độ Oxy cho ba điểm A (1; −4), B (4; 5) và C (0; −9). Điểm M di chuyển trên trục Ox. Đặt . Biết giá trị nhỏ nhất của Q có dạng , trong đó a,b là các số nguyên dương a, b < 20. Tính a – b.
Khi đo chiều dài của chiếc bàn học, một học sinh viết được kết quả: C = 118 ± 2 (cm). Sai số tỉ đối phép đo đó bằng
Cho 2 đường thẳng (d): y = – x + m + 2 và (d'): y= (m2 – 2).x + 1.
a) Khi m = – 2, hãy tìm tọa độ giao điểm của hai đường thẳng.