Cho hình thang ABCD diện tích hình thang là 225 cm2, đáy nhỏ AB = 12 cm đáy lớn CD = 18 cm. Tính diện tích tam giác ABC và tam giác ACD.
 Giải bởi Vietjack
Giải bởi Vietjack
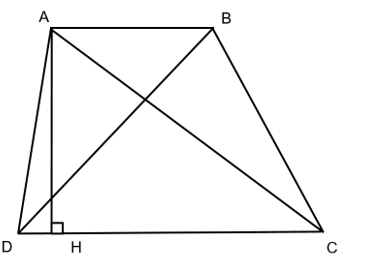
Chiều cao hình thang ABCD là: 225.2 : ( 12 + 18 ) = 15 (cm)
Ta có: Chiều cao của hình thang ABCD chính là chiều cao của hình tam giác ACD và độ dài đáy của hình tam giác ACD bằng 18 cm.
Diện tích hình tam giác ACD là : 15.18 : 2 = 135 (m2).
Diện tích hình tam giác ABC là : 225 − 135 = 90 (m2).
Cho ba điểm A (1; 1); B (2; 0); C (3; 4). Viết phương trình đường thẳng đi qua A và cách đều hai điểm B, C.
Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua C vuông góc với BD cắt Ab ở F. Chứng minh rằng D, E, F thẳng hàng.
Cho tam giác ABC vuông cân ở A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Từ C kẻ đường thẳng vuông góc với BE cắt BA ở I a) Chứng minh: BE = CI.
Cho đường tròn (O;R), và điểm A nằm ngoài đường tròn (O) sao cho OA = 2R.Vẽ tiếp tuyến AB với đường tròn (O). Gọi BH là đường cao của Δ ABO, BH cắt đường tròn (O) tại C.
a) Chứng minh: AC là tiếp tuyến của đường tròn (O).
Cho đường tròn (O; R), đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến (d) và (d’) với đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở M và cắt đường thẳng (d’) ở P. Từ O vẽ một tia vuông góc với MP và cắt (d’) ở N.
a) Chứng minh OM = OP và ∆NMP cân.
Cho tam giác ABC có , AC = 2 và . Hỏi bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?
Cho hình bình hành ABCD trong đó có AD = 2AB. Kẻ CE vuông góc với AB. Gọi M là trung điểm của AD, nối EM, kẻ MF vuông góc với CE; MF cắt BC tại N.
a) Tứ giác MNCD là hình gì?
Thị trấn A cách thị trấn B là 20 km theo đường thẳng. Một người đi xe đạp rời thị trấn A và đi đến thị trấn B với tốc độ 20 km/h. Vào đúng thời điểm đó, người đi xe đạp thứ hai rời thị trấn B đi đến thị trấn A với tốc độ 15 km/h.
a) Hai người đi xe đạp sẽ gặp nhau ở đâu giữa hai thị trấn?
Cho góc nhọn . Trên tia Ox lấy hai điểm A và C, trên tia Oy lấy hai điểm B và D, sao cho OA = OD, OC = OD (A nằm giữa O và C, B nằm giữa C và D). Chứng minh:
a) ∆OAD = ∆OBC.
Cho tam giác ABC vuông cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Các đường thẳng vuông góc kẻ từ A và E với CD cắt BC ở G và H. Đường thẳng EH và đường thẳng AB cắt nhau ở M. Đường thẳng kẻ từ A song song với BC cắt MH ở I. Chứng minh:
a) ∆ACD = ∆AME.
Trong hệ trục tọa độ Oxy cho ba điểm A (1; −4), B (4; 5) và C (0; −9). Điểm M di chuyển trên trục Ox. Đặt . Biết giá trị nhỏ nhất của Q có dạng , trong đó a,b là các số nguyên dương a, b < 20. Tính a – b.
Khi đo chiều dài của chiếc bàn học, một học sinh viết được kết quả: C = 118 ± 2 (cm). Sai số tỉ đối phép đo đó bằng