- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 33)
-
12945 lượt thi
-
51 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Phân tích đa thức thành nhân tử: 2x2 – 3x – 2.
 Xem đáp án
Xem đáp án
2x2 – 3x – 2
= 2x2 – 4x + x – 2
= (2x2 – 4x) + (x – 2)
= 2x(x – 2) + (x – 2)
= (2x + 1)(x – 2).
Câu 2:
Tính chiều cao CH của tháp ở bên kia sông biết AB = 25 m, \(\widehat {HAC} = 32^\circ \), \(\widehat {HBC} = 43^\circ \), và ba điểm A, B, H thẳng hàng. (kết quả làm tròn đến chữ số thập phân thứ nhất).

 Xem đáp án
Xem đáp án
Xét tam giác CAH vuông tại H có:
\(\tan \widehat {HAC} = \tan 32^\circ = \frac{{CH}}{{HA}} \Rightarrow HA = \frac{{CH}}{{\tan 32^\circ }}\)
Xét tam giác CBH vuông tại H có:
\(\tan \widehat {HBC} = \tan 43^\circ = \frac{{CH}}{{BH}} \Rightarrow BH = \frac{{CH}}{{\tan 43^\circ }}\)
Ta có:
\(\begin{array}{l}AB = AH - BH\\ \Rightarrow CH\left( {\frac{1}{{\tan 32^\circ }} - \frac{1}{{\tan 43^\circ }}} \right) = 25 \Rightarrow CH = \frac{{25}}{{\left( {\frac{1}{{\tan 32^\circ }} - \frac{1}{{\tan 43^\circ }}} \right)}} \approx 47,4\,\,(m)\end{array}\).
Câu 3:
Giải phương trình: \(\sqrt 3 \sin x + \cos x = 1\).
 Xem đáp án
Xem đáp án
\(\begin{array}{l}\sqrt 3 \sin x + \cos x = 1\\ \Leftrightarrow \frac{{\sqrt 3 }}{2}\sin x + \frac{1}{2}\cos x = \frac{1}{2}\\ \Leftrightarrow \sin x.\cos \frac{\pi }{6} + \cos x.\sin \frac{\pi }{6} = \frac{1}{2}\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{6}} \right) = \frac{1}{2}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{6} = \frac{\pi }{6} + k2\pi \\x + \frac{\pi }{6} = \frac{{5\pi }}{6} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\).
Câu 4:
Nghiệm của phương trình: \(\sqrt 3 \sin x - \cos x = 2\) là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
\(\begin{array}{l}\sqrt 3 \sin x - \cos x = 2\\ \Leftrightarrow \frac{{\sqrt 3 }}{2}\sin x - \frac{1}{2}\cos x = 1\\ \Leftrightarrow \sin x.\cos \frac{\pi }{6} - \cos x.\sin \frac{\pi }{6} = 1\\ \Leftrightarrow \sin \left( {x - \frac{\pi }{6}} \right) = 1\\ \Leftrightarrow x - \frac{\pi }{6} = \frac{\pi }{2} + k2\pi \,\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = \frac{{2\pi }}{3} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)
Câu 5:
Một vật hình hộp chữ nhật có kích thước (30×20×10 cm).
a) Tính thể tích của vật.
b) Tính lực đẩy Ác – si – mét tác dụng lên vật khi thả đứng nó vào trong chất lỏng có trọng lượng riêng 12000 N/m3. Biết khi đó chiều cao của vật bị chìm trong chất lỏng là 20 cm.
 Xem đáp án
Xem đáp án
a) Thể tích vật là:
V = abc = 30.20.10 = 6000 cm3 = 6.10–3 m3
b) Thể tích chìm trong chất lỏng là:
V’ = 20.20.10 = 4000 cm3 = 4.10–3 m3
Lực đẩy Ác – si – mét là:
FA = dV’ = 12000.4.10–3 = 48 N.
Câu 6:
Cho hàm số y = ax + a + 1 với a là tham số, a ≠ 0 và a ≠ –1. Tìm tất cả các giá trị của tham số a để khoảng cách từ gốc tọa độ O đến đồ thị đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
Hàm số y = ax + a + 1 có đồ thị là đường thẳng.
Với a ≠ 0 và a ≠ –1 thì đồ thị đó không đi qua gốc tọa độ O.
Gọi A là giao điểm của đồ thị với Ox nên ta có: \(A\left( {\frac{{ - a - 1}}{a};0} \right)\)
Do đó, \(OA = \left| {\frac{{a + 1}}{a}} \right|\)
Gọi B là giao điểm của d với Oy ⇒ B(0; a + 1) ⇒ OB = |a + 1|
Từ O kẻ vuông góc với AB được OH
Ta có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}\)
\( \Rightarrow \frac{1}{{O{H^2}}} = \frac{{O{B^2} + O{A^2}}}{{O{A^2}.O{B^2}}} = \frac{{{{\left( {a + 1} \right)}^2} + {{\left( {\frac{{a + 1}}{a}} \right)}^2}}}{{{{\left( {a + 1} \right)}^2}.{{\left( {\frac{{a + 1}}{a}} \right)}^2}}}\)\( = \frac{{\frac{{{a^2}{{\left( {a + 1} \right)}^2} + {{\left( {a + 1} \right)}^2}}}{{{a^2}}}}}{{\frac{{{{\left( {a + 1} \right)}^4}}}{{{a^2}}}}}\)
\( = \frac{{\left( {{a^2} + 1} \right){{\left( {a + 1} \right)}^2}}}{{{{\left( {a + 1} \right)}^4}}} = \frac{{{a^2} + 1}}{{{{\left( {a + 1} \right)}^2}}} = \frac{{{a^2} + 1}}{{{a^2} + 2a + 1}}\)
\( \Rightarrow O{H^2} = \frac{{{a^2} + 2a + 1}}{{{a^2} + 1}} = 1 + \frac{{2a}}{{{a^2} + 1}} = 1 + \frac{2}{{a + \frac{1}{a}}}\).
Với a < 0 thì OH2 ≤ 1
Với a > 0 thì:
Ta có: \(a + \frac{1}{a} \ge 2\,\,\,\forall a > 0\)
\( \Rightarrow \frac{2}{{a + \frac{1}{a}}} \le 1\,\,\forall a > 0 \Rightarrow O{H^2} = 1 + \frac{2}{{a + \frac{1}{a}}} \le 2\,\,\forall a > 0\)
Do đó, giá trị lớn nhất của OHmax ⇔ OH2max ⇔ \(a = \frac{1}{a} \Leftrightarrow {a^2} = 1 \Leftrightarrow a = 1\) (vì a > 0).
Câu 7:
Cho hàm số y = x + 1 có đồ thị là (d) và hàm số y = –x + 3 có đồ thị là (d'):
a, Vẽ (d) và (d') trên cùng 1 mặt phẳng tọa độ.
b, Hai đường thẳng (d) và (d') cắt nhau tại C và cắt trục Ox theo thứ tự A và B. Tìm tọa độ các điểm A, B, C (tìm tọa độ điểm C bằng phương pháp đại số).
c, Tính chu vi và diện tích của tam giác ABC (với đơn vị đo trên các trục tọa độ là cm).
d, Tính góc tạo bởi đường thẳng y = x + 1 với trục Ox.
 Xem đáp án
Xem đáp án
a)
Đường thẳng (d) đi qua hai điểm (0; 1) và (–1; 0).
Đường thẳng (d’) đi qua hai điểm (0; 3) và (3; 0).
Hình vẽ:
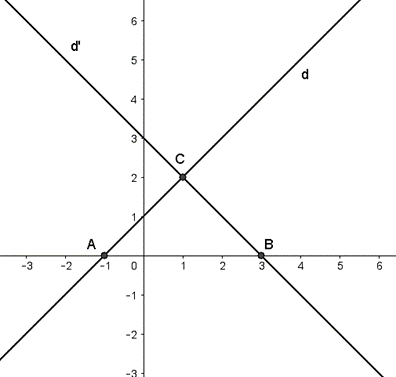
b)
Tọa độ điểm A(–1; 0) và B(3; 0) như hình vẽ.
Gọi điểm C(x0; y0)
Tọa độ của điểm C là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}{y_0} = {x_0} + 1\\{y_0} = - {x_0} + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} - {y_0} = - 1\\ - {x_0} - {y_0} = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1\\{y_0} = 2\end{array} \right.\)
Do đó, C(1; 2)
c)
Ta có:
\[\overrightarrow {AB} = \left( {4;0} \right) \Rightarrow \left| {\overrightarrow {AB} } \right| = AB = 4\] (cm)
\[\overrightarrow {AC} = \left( {2;2} \right) \Rightarrow \left| {\overrightarrow {AC} } \right| = AC = 2\sqrt 2 \] (cm)
\[\overrightarrow {BC} = \left( { - 2;2} \right) \Rightarrow \left| {\overrightarrow {BC} } \right| = BC = 2\sqrt 2 \] (cm)
Chu vi tam giác ABC là: C = AB + AC + BC = \(4 + 4\sqrt 2 \) (cm)
d)
Góc tạo bởi y = x + 1 với Ox chính là góc \(\widehat {CAB}\)
Xét tam giác ABC
Ta có:
\(\begin{array}{l}C{B^2} = C{A^2} + A{B^2} - 2CA.AB.\cos \widehat {CAB}\\ \Rightarrow \cos \widehat {CAB} = \frac{{C{A^2} + A{B^2} - C{B^2}}}{{2CA.AB}} = \frac{{{{\left( {2\sqrt 2 } \right)}^2} + {4^2} - {{\left( {2\sqrt 2 } \right)}^2}}}{{2.2\sqrt 2 .4}} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow \widehat {CAB} = 45^\circ \end{array}\)
Câu 8:
Hai tổ cùng làm một công việc nếu làm chúng thì hoàn thành trong 15 giờ. Nếu tổ 1 làm trong 5 giờ, tổ 2 làm trong 3 giờ thì đuợc 30% công việc. Hỏi nếu làm 1 mình thì mỗi tổ làm trong bao lâu ?
 Xem đáp án
Xem đáp án
Gọi số ngày tổ 1 làm một mình hết công việc là: x (giờ); số ngày tổ 2 làm một mình hết công việc là: y (giờ)
(x, y > 0)
Một ngày một mình tổ 1 làm được: \(\frac{1}{x}\) (công việc)
Một ngày một mình tổ 2 làm được: \(\frac{1}{y}\) (công việc)
Vì cả hai tổ làm chung thì 15 giờ xong nên ta có phương trình:
\(15.\left( {\frac{1}{x} + \frac{1}{y}} \right) = 1 \Rightarrow \frac{{15}}{x} + \frac{{15}}{y} = 1\) (công việc)
Vì tổ 1 làm trong 5 giờ, tổ 2 làm trong 3 giờ thì làm được 30% công việc nên ta có phương trình:
\(\frac{5}{x} + \frac{3}{y} = \frac{3}{{10}}\) (công việc)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}\frac{{15}}{x} + \frac{{15}}{y} = 1\\\frac{5}{x} + \frac{3}{y} = \frac{3}{{10}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 20\\y = 60\end{array} \right.\)
Vậy đội 1 làm một mình thì sau 20 giờ sẽ xong việc; đội 2 làm một mình thì sau 60 giờ sẽ xong công việc.
Câu 9:
Với giá trị nào của a và b thì đa thức x3 + ax2 + 2x + b chia hết cho đa thức x2 + x + 1.
 Xem đáp án
Xem đáp án
\(\begin{array}{l}{x^3} + a{x^2} + 2x + b = x\left( {{x^2} + x + 1} \right) + \left( {a - 1} \right)\left( {{x^2} + x + 1} \right) + x + b - \left( {a - 1} \right)x - \left( {a - 1} \right)\\ = \left( {x + a - 1} \right)\left( {{x^2} + x + 1} \right) + x\left( {2 - a} \right) + \left( {b - a + 1} \right)\end{array}\)
Thấy rằng bậc của x(2 – a) + (b – a + 1) nhỏ hơn bậc của x2 + x + 1 nên nó là số dư của x3 + ax2 + 2x + b chia cho x2 + x + 1
Như vậy để thỏa mãn yêu cầu để bài thì: x(2 – a) + (b – a + 1) = 0
Hay a = 2; b = 1
Vây (a; b) = (2; 1).
Câu 10:
Tìm x để \(\sqrt {2x - 1} \) có nghĩa ?
 Xem đáp án
Xem đáp án
\(\sqrt {2x - 1} \) có nghĩa \( \Leftrightarrow 2x - 1 \ge 0 \Leftrightarrow x \ge \frac{1}{2}\).
Câu 11:
Cho tam giác OAB vuông tại A, OA = 3 cm, AB = 4 cm, đường cao AH (H thuộc OB)
a) Tính AH.
b) Vẽ đường tròn (O; OA) cắt tia AH tại C. Chứng minh: CB là tiếp tuyến của đường tròn (O; OA).
 Xem đáp án
Xem đáp án
a)
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} = \frac{{25}}{{144}} \Rightarrow A{H^2} = \frac{{144}}{{25}} \Rightarrow AH = \frac{{12}}{5} = 2,4\) (cm)
b)
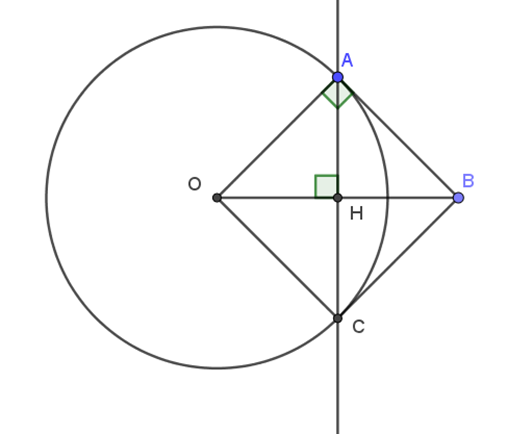
Xét đường tròn O có: OH là một phần đường kính, AC là dây cung, OH vuông góc với AC tại H nên H là trung điểm của AC
Do đó, OB là đường trung trực của AC nên ta có: AB = CB
Xét tam giác OAB và tam giác OCB có:
AB = CB
OB chung
OA = OB (cùng bằng bán kính)
Do đó, tam giác OAB bằng tam giác OCB
Do đó, ta có: \(\widehat {OCB} = \widehat {OAB} = 90^\circ \)
Vậy BC vuông góc với bán kính OC nên BC là tiếp tuyến của đường tròn tâm O
Câu 12:
Giải phương trình với ẩn số nguyên dương n thỏa mãn:
\(A_n^2 - 3C_n^2 = 15 - 5n\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có:
\(A_n^2 - 3C_n^2 = 15 - 5n\)
\(\begin{array}{l} \Leftrightarrow \frac{{n!}}{{\left( {n - 2} \right)!}} - 3.\frac{{n!}}{{\left( {n - 2} \right)!.2!}} = 15 - 5n\\ \Leftrightarrow n\left( {n - 1} \right) - \frac{3}{2}.n\left( {n - 1} \right) = 15 - 5n\end{array}\)
\( \Leftrightarrow {n^2} - n - \frac{3}{2}{n^2} + \frac{3}{2}n = 15 - 5n\)
\(\begin{array}{l} \Leftrightarrow - \frac{1}{2}{n^2} + \frac{{11}}{2}n - 15 = 0\\ \Leftrightarrow \left[ \begin{array}{l}n = 6\\n = 5\end{array} \right.\end{array}\)
Câu 13:
Có bao nhiêu cách xếp 5 nam và 5 nữ thành hàng dọc sao cho 5 nam đứng liền nhau ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Coi 5 nam là một nhóm, số cách xếp nhóm 5 bạn vào một hàng dọc 10 chỗ là: 6 cách.
Số cách hoán vị chỗ của 5 nam trong nhóm là: 5!.
Số cách hoán vị chỗ của 5 nữ cho 5 vị trí còn lại là: 5!
Vậy số cách xếp thỏa mãn yêu cầu đề bài là: 6.5!.5! = 86400.
Câu 14:
Có bao nhiêu số tự nhiên lớn hơn 4000 có 4 chữ số được lập từ các số 1, 2, 5, 7 nếu:
a) Các chữ số của số đó không nhất thiết phải khác nhau.
b) Các chữ số của số đó khác nhau.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là \(\overline {abcd} \) ở đó a, b, c, d thuộc {1; 2; 5; 7}
a)
Để số đó lớn hơn 4000 thì chữ số a phải bắt đầu bằng chữ số 5 hoặc 7.
Vậy chữ số a có 2 cách chọn, chữ số b có 4 cách chọn, chữ số c có 4 cách chọn, d cũng có 4 cách chọn.
Suy ra có tất cả các chữ số lớn hơn 4000 là 2.4.4.4 = 128 (số)
b)
Để số đó lớn hơn 4000 thì chữ số a phải bắt đầu bằng 5 hoặc 7
mà các chữ số khác nhau suy ra b có 3 cách chọn, c có 2 cách chọn và d có 1 cách chọn
Số các chữ số cần tìm là: 2.3.2.1=12 số.
Câu 15:
Tính hàm số lượng giác: \(\frac{1}{{1 + {{\tan }^2}x}} + \frac{1}{{1 + {{\cot }^2}x}}\).
 Xem đáp án
Xem đáp án
\(\begin{array}{l}\frac{1}{{1 + {{\tan }^2}x}} + \frac{1}{{1 + {{\cot }^2}x}}\\ = \frac{1}{{\frac{1}{{co{s^2}x}}}} + \frac{1}{{\frac{1}{{{{\sin }^2}x}}}} = co{s^2}x + {\sin ^2}x = 1\end{array}\)
Câu 16:
Cho hình thang ABCD có hai đường chéo AC cắt BD tại O. Tính diện tích hình thang ABCD, biết diện tích tam giác AOB là 6 cm2, diện tích tam giác AOD là 10 cm2.
 Xem đáp án
Xem đáp án
AB song song với CD
\( \Rightarrow {S_{BAD}} = {S_{ABC}} \Rightarrow {S_{BAD}} - {S_{OAB}} = {S_{ABC}} - {S_{OAB}} \Rightarrow {S_{OAD}} = {S_{OBC}} = 10c{m^2}\)
\(\frac{{OB}}{{OD}} = \frac{{{S_{OAB}}}}{{{S_{OAD}}}} = \frac{6}{{10}} = \frac{3}{5}\)
\(\frac{{{S_{OBC}}}}{{{S_{ODC}}}} = \frac{{OB}}{{OD}} = \frac{3}{5}\)
\( \Rightarrow {S_{ODC}} = \frac{5}{3}{S_{OBC}} = \frac{5}{3}.10 = \frac{{50}}{3}\left( {c{m^2}} \right)\)
\({S_{ABCD}} = {S_{OAB}} + {S_{OAD}} + {S_{OBC}} + {S_{ODC}} = 6 + 10 + 10 + \frac{{50}}{3} = \frac{{128}}{3}\left( {c{m^2}} \right)\).
Câu 17:
Phân tích \({\sin ^8}x + co{s^8}x\).
 Xem đáp án
Xem đáp án
\(\begin{array}{l}{\sin ^8}x + co{s^8}x\\ = {\left( {{{\sin }^4}x + co{s^4}x} \right)^2} - 2{\sin ^4}x.co{s^4}x\\ = {\left( {1 - 2{{\sin }^2}x.co{s^2}x} \right)^2} - \frac{1}{8}{\sin ^4}2x\\ = {\left( {1 - \frac{1}{2}{{\sin }^2}2x} \right)^2} - \frac{1}{8}{\sin ^4}2x\\ = 1 - {\sin ^2}2x + \frac{1}{8}{\sin ^4}2x\end{array}\)
\(\begin{array}{l} = 1 - \frac{{1 - cos4x}}{2} + \frac{1}{8}{\left( {\frac{{1 - cos4x}}{2}} \right)^2}\\ = 1 - \frac{{1 - cos4x}}{2} + \frac{1}{{32}}\left( {1 - 2cos4x + \frac{{1 + \cos 8x}}{2}} \right)\\ = \frac{{35}}{{64}} + \frac{7}{{16}}cos4x + \frac{1}{{64}}cos8x\end{array}\)
Câu 18:
Giải phương trình sau: \({\sin ^8}x + co{s^8}x = \frac{1}{8}\).
 Xem đáp án
Xem đáp án
Ta có:
\(\begin{array}{l}{\sin ^2}x + co{s^2}x = 1\\ \Rightarrow {\sin ^4}x + co{s^4}x = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 2{\sin ^2}x.co{s^2}x\\ = 1 - 2{\sin ^2}x.co{s^2}x\\ \Rightarrow {\sin ^8}x + co{s^8}x = {\left( {{{\sin }^4}x + co{s^4}x} \right)^2} - 2{\sin ^4}x.co{s^4}x\\ = 1 + {\sin ^4}x.co{s^4}x - 4{\sin ^2}x.co{s^2}x\\ = 1 + 2{\sin ^2}x.co{s^2}x.\left( {{{\sin }^2}x.co{s^2}x - 2} \right)\\ = 1 + \frac{{{{\sin }^2}2x}}{2}.\left( {\frac{{{{\sin }^2}2x}}{4} - 1} \right)\end{array}\)
Đặt t = sin22x (0 < t < 1)
Phương trình đã cho có dạng:
\(\begin{array}{l}1 + \frac{t}{2}\left( {\frac{t}{4} - 2} \right) = \frac{1}{8}\\ \Leftrightarrow 8 + {t^2} - 8t = 1\\ \Leftrightarrow {t^2} - 8t + 7 = 0\\ \Rightarrow \left( {t - 1} \right)\left( {t - 7} \right) = 0\\ \Leftrightarrow t = 1\,\,(TM)\end{array}\)
Với t = 1 ta có:
\({\sin ^2}2x = 1 \Rightarrow \left\{ \begin{array}{l}x = \frac{\pi }{4} + k\pi \\x = - \frac{\pi }{4} + k\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).
Câu 19:
Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có: \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \).
 Xem đáp án
Xem đáp án
Do ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} + \overrightarrow {MB} = \overrightarrow {DM} + \overrightarrow {MC} \\ \Rightarrow - \overrightarrow {MA} + \overrightarrow {MB} = - \overrightarrow {MD} + \overrightarrow {MC} \\ \Rightarrow \overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \end{array}\)
Câu 20:
Cho tam giác ABC vuông tại A (AB < AC) đường cao AH. Trên tia HC lấy điểm D sao cho HD = HA. Từ điểm D, vẽ đường thẳng vuông góc với BC cắt AC ở E. Chứng minh rằng AE = AB.
 Xem đáp án
Xem đáp án
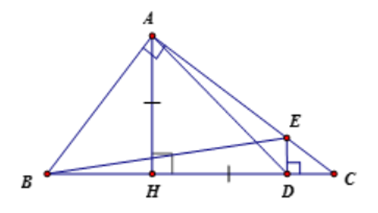
Tam giác AHD có:
HA = HD; \(\widehat {AHD} = 90^\circ \)
Do đó, tam giác AHD vuông cân
Do đó, \(\widehat {HDA} = 45^\circ \)
Tam giác CED và tam giác CBA có:
Góc \(\widehat C\) chung
\(\widehat D = \widehat A = 90^\circ \)
Do đó, tam giác CED đồng dạng với tam giác CBA (g.g)
\( \Rightarrow \frac{{CD}}{{CA}} = \frac{{CE}}{{CB}} \Rightarrow \frac{{CD}}{{CE}} = \frac{{CA}}{{CB}}\)
Xét tam giác CAD và tam giác CBE có:
\(\widehat C\) chung
\(\frac{{CD}}{{CE}} = \frac{{CA}}{{CB}}\)
Do đó, tam giác CAD đồng dạng với tam giác CBE (c.g.c)
Do đó, \(\widehat {BEC} = \widehat {ADC}\)
Ta có: \(\widehat {ADC} + \widehat {HDA} = 180^\circ \); \(\widehat {BEC} + \widehat {BEA} = 180^\circ \Rightarrow \widehat {BEC} = \widehat {ADC}\)
\( \Rightarrow \widehat {HDA} = \widehat {BEA}\) mà \(\widehat {HDA} = 45^\circ \)
\( \Rightarrow \widehat {BEA} = 45^\circ \)
Tam giác ABE có: \(\widehat A = 90^\circ ;\,\,\widehat {BEA} = 45^\circ \)
Do đó, tam giác ABE vuông cân
Do đó, AB = AE.
Câu 21:
Nếu tam giác ABC có 3 góc thỏa mãn sinA = cosB + cosC thì tam giác ABC là tam giác gì ?
 Xem đáp án
Xem đáp án
\(\sin A = \cos B + \cos C = 2cos\frac{{B + C}}{2}.cos\frac{{B - C}}{2}\)
\( = 2\sin \frac{A}{2}.cos\frac{{B - C}}{2}\)
\( \Leftrightarrow 2\sin \frac{A}{2}.cos\frac{A}{2} = 2\sin \frac{A}{2}.cos\frac{{B - C}}{2}\)
\( \Leftrightarrow cos\frac{A}{2} = cos\frac{{B - C}}{2} \Rightarrow \frac{A}{2} = \frac{{B - C}}{2}\)
\(\begin{array}{l} \Rightarrow \widehat B = \widehat A + \widehat C\\ \Rightarrow 2\widehat B = 180^\circ \Rightarrow \widehat B = 90^\circ \end{array}\)
Câu 22:
Cho biểu thức: \(P = \left( {\frac{1}{{x - \sqrt x }} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x }}{{x - 2\sqrt x - 1}}\) (với x > 0, x ≠ 1)
a) Rút gọn biểu thức P.
b) Tìm các giá trị của x để \(P > \frac{1}{2}\).
 Xem đáp án
Xem đáp án
a)
\(P = \left( {\frac{1}{{x - \sqrt x }} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x }}{{x - 2\sqrt x - 1}}\) (với x > 0, x ≠ 1)
\(P = \left( {\frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x }}{{x - 2\sqrt x - 1}}\)
\(P = \left( {\frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}} + \frac{{\sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right):\frac{{\sqrt x }}{{x - 2\sqrt x - 1}}\)
\(P = \frac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\frac{{\sqrt x }}{{x - 2\sqrt x + 1}}\)
\(P = \frac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\frac{{x - 2\sqrt x + 1}}{{\sqrt x }}\)
\(P = \frac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\frac{{x - 2\sqrt x + 1}}{{\sqrt x }}\)
\(P = \frac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }} = \frac{{\left( {1 + \sqrt x } \right)\left( {\sqrt x - 1} \right)}}{x} = \frac{{x - 1}}{x}\).
b)
\(P > \frac{1}{2} \Rightarrow \frac{{x - 1}}{x} > \frac{1}{2}\) (1)
Với x > 0, x ≠ 1 ta có:
(1)
\(\begin{array}{l} \Leftrightarrow x > 2x - 2\\ \Leftrightarrow x - 2 < 0\\ \Leftrightarrow x < 2\end{array}\)
Câu 23:
Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Gọi E, F, G, H theo thứ tự là chân Các đường vuông góc kẻ từ O đến AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
 Xem đáp án
Xem đáp án
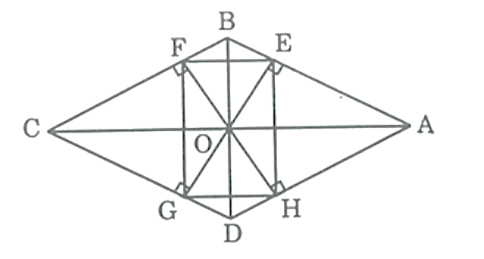
Ta có:
AB song song với CD (gt)
OE vuông góc với AB (gt)
Do đó, OE vuông góc với CD
OG vuông góc với CD (gt)
Suy ra OE trùng với OG nên ba điểm O, E, G thẳng hàng
BC song song với AD (gt)
OF vuông góc với BC (gt)
Do đó, OF vuông góc với AD
Suy ra, OF trùng với OH nên ba điểm O, H, F thẳng hàng
Vì AC và BD là đường phân giác các góc của hình thoi nên:
OE = OF (tính chất tia phân giác) (1)
OE = OH (tính chất tia phân giác) (2)
OH = OG (tính chất tia phân giác) (3)
Tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên nó là hình chữ nhật.
Câu 24:
Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, hai đường thẳng đó cắt nhau tại K.
a) Tứ giác OBKC là hình gì ? Vì sao ?
b) Chứng minh rằng AB = OK.
c) Tìm điều kiện của hình thoi ABCD để OBKC là hình vuông.
 Xem đáp án
Xem đáp án
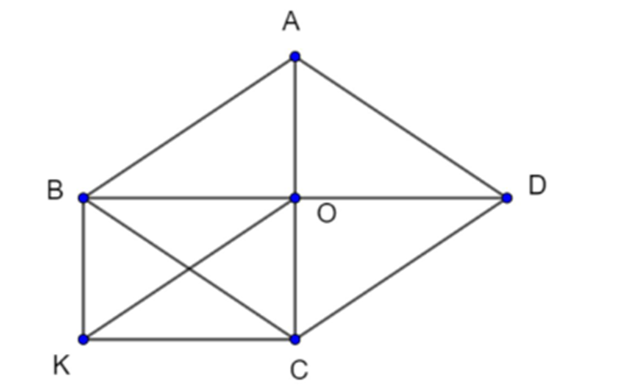
a)
Ta có tứ giác ABCD là hình thoi
Do đó, AC vuông góc với BD (tính chất 2 đường chéo trong hình thoi)
Ta có: BK song song với OC, KC song song với OB
Do đó, Tứ giác BOCK là hình bình hành
Mà \(\widehat {BOC} = 90^\circ \)
Do đó, BOCK là hình chữ nhật
b)
ABCD là hình thoi nên AB = BC = CD = DA (3)
Do OBIC là hình chữ nhật nên 2 đường chéo OI = BC (4)
Từ (3) và (4) suy ra AB = OI
c)
Để OBKC là hình vuông thì OB = OC
Do đó, ABCD phải là hình vuông.
Câu 25:
Đặt câu:
a) Có cặp quan hệ từ biểu thị mối quan gệ tương phản.
b) Có cặp quan hệ từ biểu thị mối quan hệ nguyên nhân kết quả.
c) Đặt câu sử dụng cặp quan hệ từ biểu thị quan hệ tăng tiến.
 Xem đáp án
Xem đáp án
a) Có cặp quan hệ từ biểu thị mối quan gệ tương phản
Dù học giỏi nhưng nó đã rớt cuộc thi.
b) Có cặp quan hệ từ biểu thị mối quan hệ nguyên nhân kết quả
Do đau chân nên tôi phải nghỉ tập.
c) Đặt câu sử dụng cặp quan hệ từ biểu thị quan hệ tăng tiến
Càng đau nó càng quyết tâm vượt qua.
Câu 26:
Rút gọn\(\frac{1}{{2\sqrt {x - 2} }} - \frac{1}{{2\sqrt {x + 2} }}\).
 Xem đáp án
Xem đáp án
Điều kiện xác định: x > 2
\(\frac{1}{{2\sqrt {x - 2} }} - \frac{1}{{2\sqrt {x + 2} }}\)
\( = \frac{{\sqrt {x + 2} - \sqrt {x - 2} }}{{2\sqrt {x + 2} .\sqrt {x - 2} }}\)
\( = \frac{{\sqrt {x + 2} - \sqrt {x - 2} }}{{2\sqrt {{x^2} - 4} }}\).
Câu 27:
Cho 31 số nguyên trong đó tổng của 5 số bất kỳ là một số dương. Chứng minh rằng tổng của 31 số đo là số dương.
 Xem đáp án
Xem đáp án
Trong 31 số đã cho có ít nhất 1 số là số dương (vì nếu 31 số đã cho đều âm thì tổng của 5 số bất kỳ không thể là 1 số dương)
Tách riêng số dương đó ra còn 30 số, nhóm 5 số vào 1 nhóm thì được 6 nhóm. Trong đó nhóm nào cũng là 1 số dương
Tổng của 30 số là 1 số dương cộng thêm 1 số dương đã tách.
Vậy tổng của 31 số đó là 1 số dương.
Câu 28:
Cho các hàm số y = x + 1 có đồ thị là d1 và y = – x + 3 có đồ thị là d2.
a) Vẽ đồ thị hai hàm số trên trên cùng một mặt phẳng tọa độ.
b) Gọi A, B lần lượt là giao điểm của d1, d2 với trục hoành và C là giao điểm của d1 và d2. Hãy tìm tọa độ các điểm A, B và C.
 Xem đáp án
Xem đáp án
a)
Đồ thị hàm số y = x + 1 là đường thẳng d1 đi qua hai điểm (–1; 0) và (0; 1)
Đồ thị hàm số y = –x + 3 là đường thẳng d2 đi qua hai điểm (3; 0) và (0; 3)
Vẽ hai đường thẳng d1 và d2 trên mặt phẳng Oxy như hình vẽ:
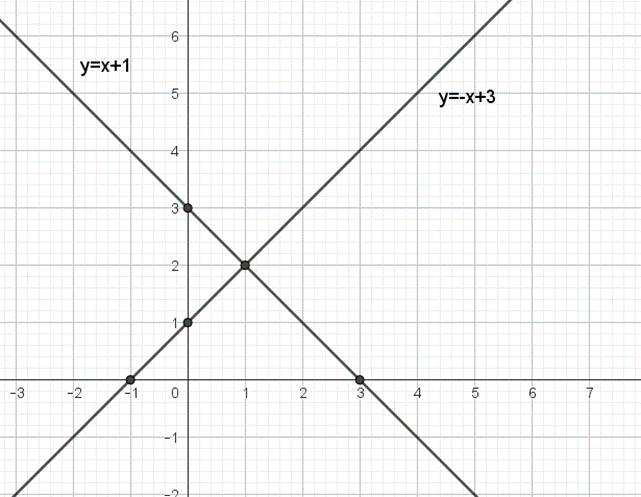
b)
Gọi A(xA; yA), B(xB; yB) lần lượt là giao điểm của d1, d2 với trục hoành và C(xC; yC) là giao điểm của d1 và d2.
Ta có:
yA = 0 ⇒ xA + 1 = 0 ⇒ xA = –1 ⇒ A(–1; 0)
yB = 0 ⇒ –xB + 3 = 0 ⇒ xB = 3 ⇒ B(3; 0)
xC là nghiệm của phương trình hoành độ giao điểm:
x + 1 = –x + 3
⇔ 2x = 2
⇔ x = 1
Do đó, xC = 1 , yC = 2 ⇒ C(1; 2).
Câu 29:
Một hình chữ nhật có chu vi là 96 cm, chiều rộng bằng \(\frac{3}{5}\) chiều dài. Tính diện tích của hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Nửa chu vi hình chữ nhật đó là:
96 : 2 = 48 (cm)
Tổng số phần bằng nhau là:
3 + 5 = 8 (phần)
Chiều dài hình chữ nhật là:
48 : 8 x 5 = 30 (cm)
Chiều rộng hình chữ nhật là:
48 : 8 x 3 = 18 (cm)
Diện tích hình chữ nhật là:
18 x 30 = 540 (cm2).
Câu 30:
Cho tứ giác ABCD. Có bao nhiêu vectơ khác vectơ không có điểm đầu và cuối là các đỉnh của tứ giác ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Một vectơ khác vectơ không được xác định bởi 2 điểm phân biệt.
Từ 4 điểm ban đầu ta có 4 cách chọn điểm đầu và 3 cách chọn điểm cuối.
Do đó; có tất cả 4.3 = 12 vecto được tạo ra.
Câu 31:
Cho tam giác ABC vuông tại A đường cao AH. Gọi O và K lần lượt là giao điểm của các đường phân giác của tam giác ABH và ACH. Vẽ AD vuông góc với OK. Chứng minh rằng các đường thẳng AD, BO, CK đồng quy.
 Xem đáp án
Xem đáp án
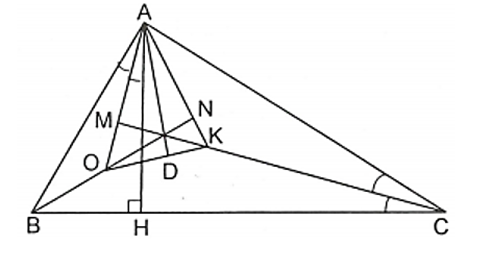
Xét tam giác ABC vuông tại A, AH vuông góc với BC nên ta có:
\(\widehat {BAH} = \widehat {ACB}\) (cùng phụ với \(\widehat {ABC}\))
Gọi M là giao điểm của AO và CK, gọi N là giao điểm của AK và BO
Vì O là giao điểm của các đường phân giác của tam giác ABH nên \(\widehat {BAO} = \widehat {HAO}\)
Vì K là giao điểm của các đường phân giác của tam giác ACH nên \(\widehat {ACK} = \widehat {BCK}\)
Xét tam giác AMC có:
\(\widehat {MAC} + \widehat {MCA} = \widehat {MAC} + \frac{{\widehat {ACB}}}{2} = \widehat {MAC} + \frac{{\widehat {BAH}}}{2} = \widehat {MAC} + \widehat {MAB} = \widehat {BAC} = 90^\circ \)
Suy ra \(\widehat {AMC} = 90^\circ \)
Do đó, CM vuông góc với AO
Chứng minh tương tự được BN vuông góc với AK
Xét tam giác AOK có AD và BO và CK là ba đường cao nên chúng đồng quy.
Câu 32:
Cho tam giác nhọn ABC, vẽ các đường cao BD, CE.
a) Chứng minh rằng: ∆ADB đồng dạng với ∆AEC.
b) Chúng minh rằng: ∆ADE đồng dạng với ∆ABC.
c) Vẽ EF vuông góc với AC tại F. Chứng minh rằng: AE.DF = AF.BE.
d) Gọi M, N lần lượt là trung điểm của các doạn thắng BD, CE. Chứng minh rằng: Hai góc BAC và MAN có chung tia phân giác.
 Xem đáp án
Xem đáp án
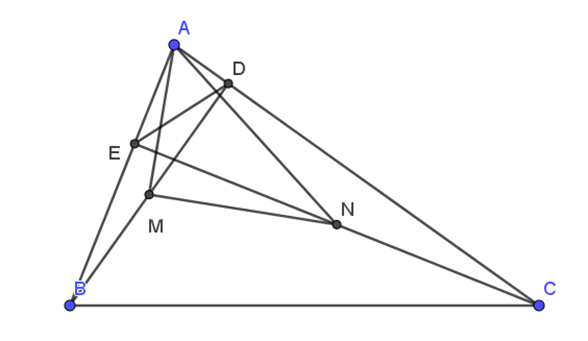
a) Xét tam giác ADB và tam giác AEC có:
\(\widehat A\) chung
\(\widehat {ADB} = \widehat {AEC} = 90^\circ \) (gt)
Do đó, tam giác ADB đồng dạng với tam giác AEC (g.g)
b) Vì tam giác ADB đồng dạng với tam giác AEC (câu a) nên ta có:
\(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\)
Xét tam giác ADE và tam giác ABC có:
\(\widehat A\) chung
\(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\) (cmt)
Do đó, tam giác ADE đồng dạng với tam giác ABC (c.g.c)
c) Ta có:
EF vuông góc với AC
BD vuông góc với AC
Do đó, EF song song với BD
Xét tam giác ADB có:
EF song song với BD
Do đó, \(\frac{{AE}}{{EB}} = \frac{{AF}}{{FD}}\) (định lý Talet)
Hay: AE. FD = AF.BE
d)
M là trung điểm BD nên BD = 2MB
N là trung điểm CE nên CE = 2NC
Vì tam giác ADB đồng dạng với tam giác AEC (câu a)
Do đó, \(\frac{{AB}}{{AC}} = \frac{{DB}}{{EC}} = \frac{{MB}}{{NC}}\).
Gọi H là giao điểm của hai đường cao BD và CE.
Xét tam giác HEB và tam giác HDC có:
\(\widehat {HEB} = \widehat {HDC} = 90^\circ \)
\(\widehat {EHB} = \widehat {DHC}\) (đối đỉnh)
Do đó, tam giác HEB đồng dạng với tam giác HDC (g.g)
Nên: \(\widehat {EBD} = \widehat {DCE}\) (2 góc tương ứng)
Xét tam giác AMB và tam giác ANC có:
\(\widehat {ABM} = \widehat {ACN}\)
\(\frac{{AB}}{{AC}} = \frac{{MB}}{{NC}}\)
Tam giác AMB đồng dạng với tam giác ANC (c.g.c)
\( \Rightarrow \widehat {BAM} = \widehat {CAN}\)
Do đó, hai góc BAC và góc MAN có cùng tia phân giác.
Câu 33:
Cho ∆ABC vuông tại A (AB < AC), E là trung điểm của BC. Kẻ EF vuông góc với AB tại F, ED vuông góc với AC tại D. Gọi O là giao điểm của AE và DF.
a) Chứng minh rằng tứ giác ADEF là hình chữ nhật.
b) Gọi K là điểm đối xứng của E qua D. Chứng minh tứ giác AECK là hình thoi.
c) Chứng minh rằng ba điểm B, O, K thẳng hàng.
d) Kẻ EM vuông góc với AK tại M. Chứng minh: \(\widehat {DMF} = 90^\circ \).
 Xem đáp án
Xem đáp án
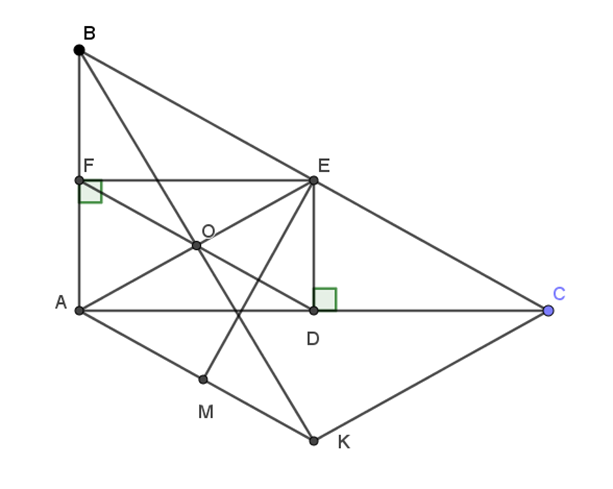
a)
EF vuông góc với AB do đó \(\widehat {AFE} = 90^\circ \)
ED vuông góc với AC do đó \(\widehat {ADE} = 90^\circ \)
Tứ giác ADEF có:
\(\widehat {FAD} = 90^\circ \)
\(\widehat {AFE} = 90^\circ \)
\(\widehat {ADE} = 90^\circ \)
Do đó, ADEF là hình chữ nhật
b)
K đối xứng với E qua D
Do đó D là trung điểm của EK
ED vuông góc với AC, AB vuông góc với AC
Do đó, ED song song với AB
Tam giác ABC có:
E là trung điểm của BC
ED song song với AB
Do đó, D là trung điểm của AC
Tứ giác AECK có:
D là trung điểm của AC, EK
Do đó, AECK là hình bình hành mà EK vuông góc với AC
Do đó, AECK là hình thoi
c)
ADEF là hình chữ nhật, DF và AE giao nhau tại O
Nên O là trung điểm của DF, AE và DF = AE
AECK là hình thoi nên AK = EC, AK song song với EC
AK = EC, BE = EC nên AK = BE
Tứ giác ABEK có:
AK = BE
AK song song với BE
Do đó, ABEK là hình bình hành
Do đó, AE, BK cắt nhau tại trung điểm mỗi đường
Mà O là trung điểm của AE, O là trung điểm của BK
Do đó, B, O, K thẳng hàng
d)
Tam giác AME vuông tại M có MO là đường trung tuyến
\(MO = \frac{1}{2}AE = \frac{1}{2}DF\)
Tam giác FMD có:
\(MO = \frac{1}{2}DF\)
MO là đường trung tuyến
Do đó, FMD vuông tại M
\( \Rightarrow \widehat {DMF} = 90^\circ \)
Câu 34:
Tính căn bậc 2 của số thực n trong C.
 Xem đáp án
Xem đáp án
#include <stdio.h>
#include <math.h>
int main()
{
int a = 13; //Gắn giá trị cần khai căn, hoặc có thể cho nhập từ bàn phím
float cb2 = (float)sqrt(a);//Tính căn bậc 2 của a
printf("can ba 2 cua so %d la: %f",a, cb2); //Hiển thị kết quả
}
Câu 35:
Cho tam giác ABC, AH vuông góc với BC, AH = 12cm, AB = 15cm, CH = 16cm.
a) Tính độ dài BH, AC.
b) Tam giác ABC có phải là tam giác vuông không? Vì sao?
 Xem đáp án
Xem đáp án
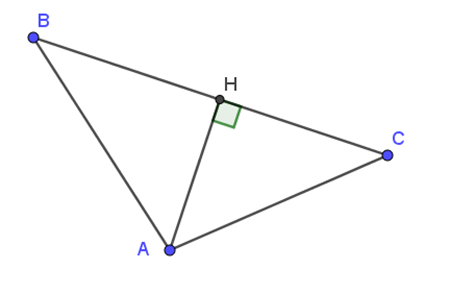
a)
Xét tam giác AHB vuông tại H
Áp dụng định lí Py–ta–go ta có:
AH2 + BH2 = AB2
\( \Rightarrow BH = \sqrt {A{B^2} - A{H^2}} = \sqrt {{{15}^2} - {{12}^2}} = 9\) (cm)
Xét tam giác AHC vuông tại H
Áp dụng định lí Py–ta–go ta có:
AH2 + CH2 = AC2
\( \Rightarrow AC = \sqrt {C{H^2} + A{H^2}} = \sqrt {{{16}^2} + {{12}^2}} = 20\) (cm)
b)
Xét tam giác ABC có:
BC = BH + CH = 9 + 16 = 25 (cm)
\(A{B^2} + A{C^2} = {15^2} + {20^2} = 625 = {25^2} = B{C^2}\)
Do đó, theo định lý Py–ta–go đảo thì tam giác ABC vuông tại A.
Câu 36:
Cho tam giác ABC, vẽ AH vuông góc vs BC (H thuộc BC), trên tia AH lấy D sao cho AH = HD. Chứng minh:
a) Tam giác ABH bằng tam giác DBH.
b) AC = CD.
c) Qua A kẻ đg thẳng song song vs BD cắt BC tại E. Chứng minh H là trung điểm của BE.
 Xem đáp án
Xem đáp án
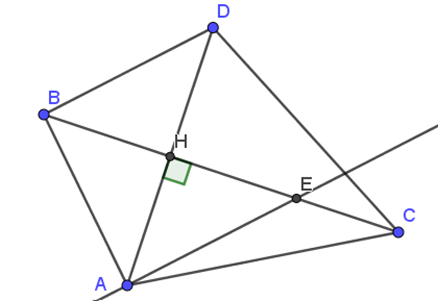
a)
Xét ΔBHA vuông tại H và ΔBHD vuông tại H có
BH chung
HA = HD
Do đó, tam giác BHA bằng tam giác BHD
b)
Xét tam giác CAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA = CD
c)
Xét ΔAHE vuông tại H và ΔDHB vuông tại H có
HA = HD
\(\widehat {HAE} = \widehat {HDB}\)
Do đó, tam giác AHE bằng tam giác DHB
Suy ra: HE = HB
Hay H là trung điểm của BE.
Câu 37:
Tính nhanh: \(\left( {1 - \frac{1}{4}} \right) \times \left( {1 - \frac{1}{5}} \right) \times \left( {1 - \frac{1}{6}} \right)\, \times \left( {1 - \frac{1}{7}} \right) \times \left( {1 - \frac{1}{8}} \right)\).
 Xem đáp án
Xem đáp án
\(\left( {1 - \frac{1}{4}} \right) \times \left( {1 - \frac{1}{5}} \right) \times \left( {1 - \frac{1}{6}} \right)\, \times \left( {1 - \frac{1}{7}} \right) \times \left( {1 - \frac{1}{8}} \right)\)
\( = \frac{3}{4} \times \frac{4}{5} \times \frac{5}{6} \times \frac{6}{7} \times \frac{7}{8}\)
\( = \frac{{3 \times 4 \times 5 \times 6 \times 7}}{{4 \times 5 \times 6 \times 7 \times 8}} = \frac{3}{8}\).
Câu 38:
Cho hai khoảng A = (m; m + 1) và B = (3; 5). Tìm m để A ∪ B là một khoảng. Hãy xác định khoảng đó.
 Xem đáp án
Xem đáp án
A ∪ B là một khoảng khi A ∩ B = Ø
Khi đó:
5 ≤ m hoặc m + 1 ≤ 3 ⇔ m ≤ 2 hoặc m ≥ 5
Do đó: A ∪ B là một khoảng ⇔ 2 < m < 5
Khi đó: Nếu 2 < m ≤ 3 thì A ∪ B = (m; 5)
Nếu 3 < m ≤ 4 thì A ∪ B = (3; 5)
Nếu 4 < m ≤ 5 thì A ∪ B = (3; m + 1).
Câu 39:
Tìm m để hệ bất phương trình sau có nghiệm là một đoạn có độ dài bằng 3 trên trục số.
a) \(\left\{ \begin{array}{l}{x^2} + 2x - 24 \le 0\\5x + 3m + 1 \ge 0\end{array} \right.\).
b) \(\left\{ \begin{array}{l}{x^2} - 8x + 7 \le 0\\{x^2} - \left( {2m + 1} \right)x + {m^2} + m \le 0\end{array} \right.\).
 Xem đáp án
Xem đáp án
Để hệ phương trình có độ dài là một đoạn có độ dài bằng 3. Ta cần tìm một số k sao cho:
k ≤ x ≤ k + 3
a)
\(\begin{array}{l}\left\{ \begin{array}{l}{x^2} + 2x - 24 \le 0\\5x + 3m + 1 \ge 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left( {x + 6} \right)\left( {x - 4} \right) \le 0\\x \ge \frac{{ - 3m - 1}}{5}\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l} - 6 \le x < 4\\x \ge \frac{{ - 3m - 1}}{5}\end{array} \right. \Rightarrow \frac{{ - 3m - 1}}{5} \le x \le 4\\ \Rightarrow \frac{{ - 3m - 1}}{5} = 1 \Rightarrow m = - 2\end{array}\)
b)
\(\left\{ \begin{array}{l}{x^2} - 8x + 7 \le 0\\{x^2} - \left( {2m + 1} \right)x + {m^2} + m \le 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 1} \right)\left( {x - 7} \right) \le 0\\\left( {x - m} \right)\left( {x - m - 1} \right) \le 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}1 \le x \le 7\\m \le x \le m + 1\end{array} \right.\)
Do m ≤ x ≤ m + 1 nên độ dài đoạn thẳng biểu diễn tập nghiệm là 1 nên không tồn tại m thỏa mãn yêu cầu đề bài.
Câu 40:
Tính tổng: S1 = 1 + 2 + 3 + ... + 999.
 Xem đáp án
Xem đáp án
Số các số hạng của S1 là: (999 – 1) : 1 + 1 = 999 ( số hạng )
Tổng S1 = (999 + 1) × 999 : 2 = 499500.
Câu 41:
Tìm tập xác định của hàm số: \(y = \frac{{cos2x}}{{\tan x - 1}}\).
 Xem đáp án
Xem đáp án
Điều kiện xác định của hàm số là:
\(\left\{ \begin{array}{l}\cos x \ne 0\\\tan x \ne - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne - \frac{\pi }{4} + k\pi \\x \ne \frac{\pi }{2} + k\pi \end{array} \right.\)
Do đó, \(D = \mathbb{R}\backslash \left\{ { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right\}\).
Câu 42:
Một hình chữ nhật có cạnh này bằng \(\frac{2}{3}\) cạnh kia. Nếu bớt đi mỗi cạnh 5m thì diện tích hình chữ nhật đó giảm đi 16%. Tính kích thước của hình chữ nhật đó ?
 Xem đáp án
Xem đáp án
Gọi chiều dài hình chữ nhật là x (m, x > 5)
Suy ra chiều rộng hình chữ nhật là \(\frac{2}{3}x\) (m)
Diện tích hình chữ nhật ban đầu là: \(\frac{2}{3}{x^2}\) (m2)
Nếu bớt đi mỗi cạnh 5m thì diện tích giảm đi 16% nên ta có phương trình:
\(\begin{array}{l}\left( {x - 5} \right)\left( {\frac{2}{3}x - 5} \right) = \frac{2}{3}{x^2} - 16\% .\frac{2}{3}{x^2}\\ \Leftrightarrow - 5x - \frac{{10}}{3}x + 25 = - 16\% .\frac{2}{3}{x^2}\\ \Leftrightarrow \frac{8}{{75}}{x^2} - \frac{{25}}{3}x + 25 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{25}}{8}\left( {KTM} \right)\\x = 75\left( {TM} \right)\end{array} \right.\end{array}\)
Vậy diện tích hình chữ nhật là: \(75.\frac{2}{3}.75 = 3750\) (m2).
Câu 43:
Tìm m để \( - 9 < \frac{{3{x^2} + mx - 6}}{{{x^2} - x + 1}} < 6\) nghiệm đúng với mọi x ∈ ℝ.
 Xem đáp án
Xem đáp án
Bất phương trình đã cho tương ứng với:
\( - 9\left( {{x^2} - x + 1} \right) < 3{x^2} + mx - 6 < 6\left( {{x^2} - x + 1} \right)\)
\( \Leftrightarrow \left\{ \begin{array}{l}12{x^2} + \left( {m - 9} \right)x + 3 > 0\,\,\left( 1 \right)\\3{x^2} - \left( {m + 6} \right)x + 12 > 0\,\,\left( 2 \right)\end{array} \right.\)
Yêu cầu đề bài tương đương với (1) và (2) nghiệm đúng với mọi x thuộc ℝ
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta (1) < 0\\\Delta (2) < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 9} \right)^2} - 144 < 0\\{\left( {m + 6} \right)^2} - 144 < 0\end{array} \right. \Leftrightarrow - 3 < m < 6\).
Câu 44:
Cho hệ phương trình: \(\left\{ \begin{array}{l}9{x^2} - 16{y^2} = 144\\x - y = m\end{array} \right.\). Tìm m để hệ có nghiệm duy nhất.
 Xem đáp án
Xem đáp án
\(\begin{array}{l}\left\{ \begin{array}{l}9{x^2} - 16{y^2} = 144\\x - y = m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9{\left( {m + y} \right)^2} - 16{y^2} = 144\\x = m + y\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}9{y^2} + 18my + 9{m^2} - 16{y^2} = 144\\x = m + y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 7{y^2} + 18my - 144 = 0(1)\\x = m + y\end{array} \right.\end{array}\)
Để (1) có 1 nghiệm duy nhất thì \(\Delta ' = 0 \Leftrightarrow 9{m^2} - ( - 7).( - 144) = 0 \Leftrightarrow m = 4\sqrt 7 \)
Câu 45:
Tìm a, b để hệ phương trình \(\left\{ \begin{array}{l}ax + by = 5\\\left( {2 - a} \right)x + \left( {3 - b} \right)y = 4\end{array} \right.\) có nghiệm (–3; 4)
 Xem đáp án
Xem đáp án
\(\left\{ \begin{array}{l}ax + by = 5\\\left( {2 - a} \right)x + \left( {3 - b} \right)y = 4\end{array} \right.\) có nghiệm (–3; 4)
\( \Leftrightarrow \left\{ \begin{array}{l} - 3a + 4b = 5\\(2 - a).( - 3) + (3 - b).4 = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3a - 4b = - 5\\3a - 4b = - 2\end{array} \right.\)
Do đó, hệ phương trình vô nghiệm.
Vậy không có giá trị nào của a và b thỏa mãn yêu cầu đề bài
Câu 46:
Một máy bơm bơm đầy bình nước hết 5 giờ , một máy bơm khác bơm đầy cùng bình đó hết 3 giờ. Hỏi nếu 2 máy bơm cùng nhau thì sau bao lâu thì đầy \(\frac{2}{3}\) bình.
 Xem đáp án
Xem đáp án
Máy 1 trong 1 giờ bơm được: \(\frac{1}{5}\) bình
Máy 2 trong 1 giờ bơm được: \(\frac{1}{3}\) bình
Hai máy bơm 1h được \(\frac{1}{5} + \frac{1}{3} = \frac{8}{{15}}\) (h)
Vậy muốn bơm \(\frac{2}{3}\) bình thì cần số thời gian là: \(\frac{2}{3}:\frac{8}{{15}} = \frac{5}{4}\left( h \right)\)
Câu 47:
Cho tam giác ABC, M là điểm trên cạnh BC sao cho BM = 2MC. Chứng minh rằng: \(AM = \frac{1}{3}AB + \frac{2}{3}AC\)
 Xem đáp án
Xem đáp án
Vì MB = 2MC (M thuộc BC)
\[ \Rightarrow \overrightarrow {MB} = - 2\overrightarrow {MC} \]
\[ \Rightarrow \overrightarrow {MA} + \overrightarrow {AB} = - 2\overrightarrow {MA} - 2\overrightarrow {AC} \]
\[ \Rightarrow 3\overrightarrow {AM} = \overrightarrow {AB} + 2\overrightarrow {AC} \]
\[ \Rightarrow \overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \].
Câu 48:
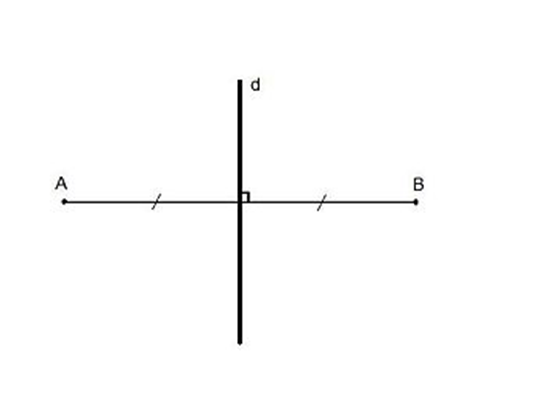
1. Hai điểm đối xứng qua một đường thẳng khi nào ?
2. Hai hình đối xứng qua một đường thẳng khi nào ?
3. Cho 1 số ví dụ về hình có trục đối xứng và chỉ ra trục đối xứng của nó.
 Xem đáp án
Xem đáp án
Khi đường thẳng d là đường trung trực của đoạn thẳng AB thì điểm A đối xứng với điểm B qua đường thẳng d. Khi đó đường thẳng d gọi là trục đối xứng của hai điểm A và B.
Câu 49:
Độ dài tập nghiệm [a; b] của bất phương trình \({3^{\sqrt {x + 1} }} \ge 81\sqrt {{{\left( {\frac{1}{9}} \right)}^{5 - \frac{x}{4}}}} \) là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Bất phương trình đã cho tương đương với:
\({3^{\sqrt {x + 1} }} \ge {3^4}.\sqrt {{9^{\frac{x}{4} - 5}}} \Leftrightarrow {3^{\sqrt {x + 1} }} \ge {3^{\frac{x}{4} - 1}} \Leftrightarrow 4\sqrt {x + 1} \ge x - 1\)
\( \Leftrightarrow \left[ \begin{array}{l}x < 1\\x \ge - 1\\\left\{ \begin{array}{l}x \ge 1\\0 \le x \le 24\\x \ge - 1\end{array} \right.\end{array} \right. \Leftrightarrow - 1 \le x \le 24\)
Ta có: 24 – (– 1) = 25.
Câu 50:
Rút gọn phân thức: \(\frac{{20{x^2}{y^2}}}{{15x{y^7}}}\).
 Xem đáp án
Xem đáp án
\(\frac{{20{x^2}{y^2}}}{{15x{y^7}}} = \frac{{5.4.x.x.{y^2}}}{{5.3.x.{y^2}.{y^5}}} = \frac{{4x}}{{3{y^2}}}\).
Câu 51:
Mỗi người sử dụng máy tính dùng password có 6 đến 8 kí tự. Các ký tự có thể là chữ số hoặc chữ cái, mỗi password phải có ít nhất 01 chữ số. Tìm tổng số password có thể có.
 Xem đáp án
Xem đáp án
Phân biệt chữ thường với chữ hoa
Chữ cái thường: 26
Chữ cái hoa: 26
Chữ số: 10
Do đó, tổng cộng: 26 + 26 + 10 = 62 (ký tự khác nhau)
Nếu password có n ký tự thì ta có:
Tổng số trường hợp là: 62n
Số trường hợp không có chữ số là: 522
Vậy số trường hợp có ít nhất 1 chữ số là: 62n – 52n
Với n = 6, 7, 8 ta có tổng số trường hợp là:
n = n6 + n7 + n8 = 626 – 526 + 627 – 527 + 628 – 528
= 167410949583040.
