Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình.
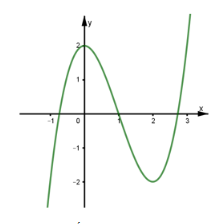
Gọi m là số nghiệm của phương trình f(f(x)) = 1. Khẳng định nào sau đây là đúng?
A. m = 6;
B. m = 7;
C. m = 5;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Đặt f(x) = u khi đó nghiệm của phương trình f(f(x)) = 1 chính là hoành độ giao điểm của đồ thị f(u) với đường thẳng y = 1.
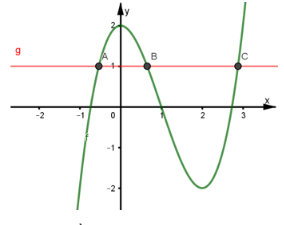
Dựa vào đồ thị ta có ba nghiệm:
Với u1 ∈ (-1; 0), u2 ∈ (0; 1), u3 ∈ ( ; 3)
Tiếp tục xét số giao điểm của đồ thị hàm số f(x) với từng đường thẳng y = u1, y = u2, y = u3.
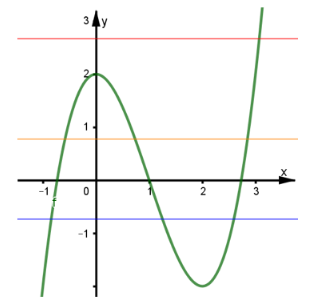
Dựa vào đồ thị ta có được 7 giao điểm.
Suy ra phương trình ban đầu f(f(x)) = 1 có 7 nghiệm
Cho đoạn thẳng AB và M là một điểm nằm trên đoạn AB sao cho AM = AB. Giá trị của k để có đẳng thức là:
Hình nón có thiết diện qua trục là tam giác đều và có thể tích . Diện tích xung quanh S của hình nón đó là:
Cho hình hộp ABCD.A’B’C’D’. Gọi M là điểm trên cạnh AC sao cho AC = 3MC. Lấy N trên cạnh C’D sao cho C’N = xC’D. Với giá trị nào của x thì MN // BD’.
Một hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước là 2 cm, 3 cm và 6 cm. Thể tích của khối tứ diện ACB’D’ bằng:
Cho tam giác ABC đều cạnh a. Gọi M là trung điểm BC. Khẳng định nào sau đây đúng?
Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Kẻ 2 tiếp tuyến AM, AN và cát tuyến ABC với đường tròn (AB < AC). Qua O kẻ OK vuông góc với BC tại K, OK cắt MN tại S. Chứng minh SC là tiếp tuyến của đường tròn (O).
Cho tứ diện ABCD có I, J lần lượt là trung điểm AC, BC. Gọi K thuộc BD sao cho KD < KB. Gọi E là giao điểm của JK và CD, F là giao điểm của AD và IE. Giao tuyến của (IJK) và (ACD) là:
Tìm m nguyên để hệ phương trình sau có nghiệm duy nhất là nghiệm nguyên.
a)
Trong hệ trục tọa độ Oxy cho hình bình hành OABC, điểm C thuộc trục hoành. Khẳng định nào sau đây đúng?