Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a, CD = a . Góc giữa 2 mặt phẳng (SBC) và (ABCD) bằng 60° .Gọi I là trung điểm của cạnh AD. Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt đáy. Tính thể tích khối chóp SABCD theo a.
Giải bởi Vietjack
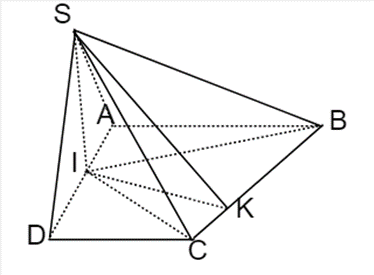
Do (SBI) ⊥ (ABCD), (SCI) ⊥ (ABCD) ⇒ SI ⊥ (ABCD)
Kẻ IK ⊥ BC (K thuộc BC) ⇒ BC ⊥ (SIK) ⇒ \[\widehat {SKI} = {60^{\rm{o}}}\]
Diện tích hình thang ABCD bằng: 3a2
Tổng diện tích ∆ABI và ∆CDI bằng \[\frac{{3{a^2}}}{2}\]⇒ S∆IBC = \[\frac{{3{a^2}}}{2}\]
\[BC = \sqrt {{{\left( {AB - CD} \right)}^2} + A{D^2}} = a\sqrt 5 \]
\[ \Rightarrow IK = \frac{{2{S_{\Delta IBC}}}}{{BC}} = \frac{{3\sqrt 5 a}}{5}\]
\[ \Rightarrow SI = IK.\tan \widehat {SKI} = \frac{{3\sqrt {15} a}}{5}\]
Thể tích khối chóp S.ABCD là: \[V = \frac{1}{3}{S_{ABCD}}.SI = \frac{{3\sqrt {15} {a^2}}}{5}\].
Lớp 10A có 45 học sinh, trong đó 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào trong 3 môn trên và 5 em thích cả 3 môn. Hỏi có bao nhiêu em thích 1 môn trong 3 môn trên?
Cho tập hợp A = (0; +∞) và B = {x ∈ ℝ | mx2 ‒ 4x + m ‒ 3 = 0}. Tìm m để B có đúng hai tập con và B ⊂ A.
Cho tam giác ABC vuông cân tại A, \[AB = \sqrt 2 \]. Về phía ngoài tam giác vẽ tam giác ACD vuông cân tại D .
a) Tứ giác ABCD là hình gì? Vì sao?
b) Tính diện tích ABCD.
Giải phương trình: \[3\sin \left( {4x + \frac{\pi }{3}} \right) - 4 = 0\].
Chứng minh rằng mọi hàm số f(x) có tập xác định đối xứng, đều có thể viết dưới dạng tổng của một hàm số chẵn và một hàm số lẻ.
Từ các số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số có 3 chữ số khác nhau chia hết cho 3.
Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ (M ∈ OP), IN // OP (N ∈ OQ). Chứng minh rằng:
a) Tam giác IMN cân tại I.
b) OI là đường trung trực của MN.
Một đội công nhân 9 người trong một ngày đắp được 60 mét đường. Người ta bổ sung thêm 18 người nữa cùng đắp thì trong một ngày đắp được bao nhiêu mét đường đó (mức đắp mỗi người như nhau)?
Một hộ nông dân trồng đậu và cà trên diện tích 8a. Nếu trồng đậu thì cần 20 công và thu 3 000 000 đồng trên một a, nếu trồng cà thì cần 30 công và thu 40 000 000 đồng trên một a. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180?
Tìm một số có hai chữ số, biết rằng nếu viết chữ số 0 xen giữa hai chữ số của số đó thì được một số có ba chữ số, gấp 9 lần số ban đầu. Tìm số đã cho.
Nêu mệnh đề phủ định và xét tính đúng sai của mệnh đề sau:
A: “Với mọi n ∈ ℕ*, (1 + 2 + .... + n) không chia hết cho 11”.
Rút gọn phân thức: \[\frac{{{a^2} + {b^2} - {c^2} + 2ab}}{{{a^2} - {b^2} + {c^2} + 2ac}}\].
