Trong kì thi đánh giá năng lực lần I năm học 2018 – 2019 của trường THPT Triệu Quang Phục, kết quả có 86 thí sinh đạt điểm giỏi môn Toán, 61 thí sinh đạt điểm giỏi môn Vật Lí và 76 thí sinh đạt điểm giỏi môn Hóa Học, 45 thí sinh đạt điểm giỏi cả hai môn Toán và Vật Lí, 21 thí sinh đạt điểm giỏi cả hai môn Vật Lí và Hóa Học, 32 thí sinh đạt điểm giỏi cả hai môn Toán và Hóa Học, 18 thí sinh đạt điểm giỏi cả ba môn Toán, Vật Lí và Hóa Học. Có 782 thí sinh mà cả ba môn đều không điểm giỏi. Hỏi trường THPT Triệu Quang Phục có bao nhiêu thí sinh tham dự kì thi đánh giá năng lực lần I năm học 2018 –2019?
A. 920;
B. 912;
C. 925;
D. 889.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là C
Ta biểu diễn các tập hợp như trong biểu đồ: Thí sinh đạt điểm giỏi môn Toán được biểu diễn màu trắng, Thí sinh đạt điểm giỏi môn Vật Lý được biểu diễn màu xanh. Thí sinh đạt điểm giỏi môn Hóa được biểu diễn màu hồng. Mỗi tập hợp nhỏ bên trong gọi tên như trong hình.
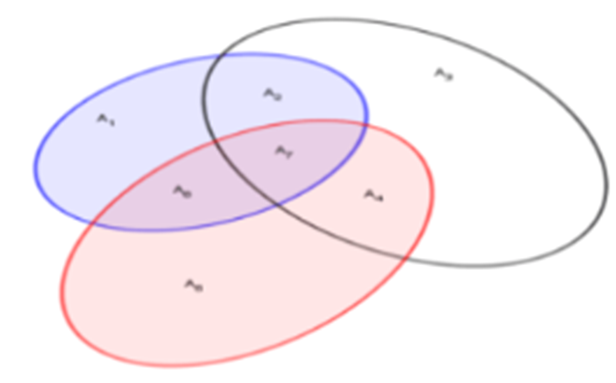
Ta có số thí sinh đạt điểm giỏi cả ba môn Toán, Vật Lí và Hóa Học là
n(A7) = 18
45 thí sinh đạt điểm giỏi cả hai môn Toán và Vật Lí ta được
n(A7) + n(A2) = 45
32 thí sinh đạt điểm giỏi cả hai môn Toán và Hóa Học ta được
n(A7) + n(A4) = 32
21 thí sinh đạt điểm giỏi cả hai môn Vật Lí và Hóa Học ta được
n(A7) + n(A6) = 21
Số thí sinh đạt điểm giỏi chỉ hai môn là
n(A6) + n(A4) + n(A2) = n(A7) + n(A2) + n(A7) + n(A4) + n(A7) + n(A6) – 3n(A7)
= 45 + 32 + 21 – 3 . 18 = 44
86 thí sinh đạt điểm giỏi môn Toán ta được
n(A3) + n(A4) + n(A2) + n(A7) = 86
61 thí sinh đạt điểm giỏi môn Vật Lí ta được
n(A1) + n(A6) + n(A2) + n(A7) = 61
76 thí sinh đạt điểm giỏi môn Hóa Học ta được
n(A4) + n(A6) + n(A5) + n(A7) = 76
Số thí sinh đạt điểm giỏi chỉ một môn là
n(A1) + n(A3) + n(A5)
= 86 + 61 + 76 – 3n(A7) – 2[n(A6) + n(A4) + n(A2)]
= 86 + 61 + 76 – 3 . 18 – 2 . 44 = 81
Số thí sinh đạt điểm giỏi gồm
n(A1) + n(A2) + n(A3) + n(A4) + n(A5) + n(A6) + n(A7)
= [n(A1) + n(A3) + n(A5)] + [n(A6) + n(A4) + n(A2)] + n(A7)
= 81 + 44 + 18 = 143
Trường THPT Triệu Quang Phục có số thí sinh tham dự kì thi đánh giá năng lực lần I
năm học 2018 – 2019 bao gồm số thí sinh đạt điểm giỏi và số thí sinh không đạt điểm giỏi nên bằng: 782 + 143 = 925 (thí sinh)
Vậy ta chọn đáp án C.
Cho tam giác ABC, có AB = AC. AM là tia phân giác của góc A
a) Chứng minh DAMB = DAMC.
b) Chứng minh M là trung điểm của BC.
c) Cho biết Ax là tia phân giác góc ngoài của đỉnh A. Chứng minh Ax // BC.
Chứng minh rằng trong tam giác ABC ta có các hệ thức:
sin A = sinB.cosC + sinC.cosB.
Tam giác ABC vuông tại A, gọi I là giao điểm của các đường phân giác.
a) Biết AB = 5, IC = 6. Tính BC.
b) Biết \(IB = \sqrt 5 ,IC = \sqrt {10} \).Tính độ dài AB, AC.
Cho tam giác ABC vuông tại A, đường cao AH.
a) AB = 6 cm, BC = 10 cm. Tính AC, BH, HC, AH.
b) BH = 1 cm, AH = 2 cm. Tính HC, AC, BA, BC.
c) BH = 4 cm, HC = 9 cm. Tính BC, AB, AH, AC.
d) BH = 9 cm, AC = 20 cm. Tính HC, AH, AB, BC.
Cho tam giác ABC có \(\widehat A = 90^\circ \). Từ trung điểm E của cạnh AC kẻ EF vuông góc với BC. Nối AF với BE.
a) Chứng minh AF = BE . cosC.
b) Biết BC =10 cm, sinC = 0,6. Tính diện tích tứ giác ABFE.
c) AF và BE cắt nhau tại O. Tính sin góc AOB.
Tìm các số tự nhiên x biết
a) x thuộc B(8) và x ≥ 30.
b) x chia hết cho 9 và x < 40.
c) x chia hết cho 6, x chia hết cho 21 và x < 200.
d) x chia hết cho 5, x chia hết 7, x chia hết cho 8 và ≥ 500.
e) 150 chia hết cho x , 120 chia hết cho x và x lớn nhất.
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
giải phương trình:
a) 2sin2x + sinx = 0;
b) sinx + cos3x = 0;
c) sinx + 2cosx = 0;
d) 2sin2 3x = 1;
e) cos2x = 2cosx – 1.
Cho tam giác ABC vuông tại A, đường cao AH. Biết diện tích tam giác ABH và ACH lần lượt là 54 cm2 và 96 cm2. Tính độ dài BC.
Một người mua 5 m vải hết 100 000 đồng. Hỏi người đó mua 7,5 m vải cùng loại thì phải trả bao nhiêu tiền?
Cho tứ diện S.ABC. Gọi O là điểm thuộc miền trong của tam giác ABC. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh SA, SC sao cho MN không song song với AC. Tìm thiết diện do (MNO) cắt tứ diện S.ABC.
Rút gọn
a) \(\sqrt {8 + 2\sqrt 7 } - \sqrt {8 - 2\sqrt 7 } \);
b) \(\sqrt {3 + 2\sqrt 2 } - \sqrt {6 - 4\sqrt 2 } \).
Một tam giác có độ dài 3 cạnh là 13, 14, 15. Tính diện tích của tam giác đó.
Cho tam giác ABC. Chứng minh rằng \(1 + \frac{r}{R} = \cos A + \cos B + \cos C\).