Giải bởi Vietjack
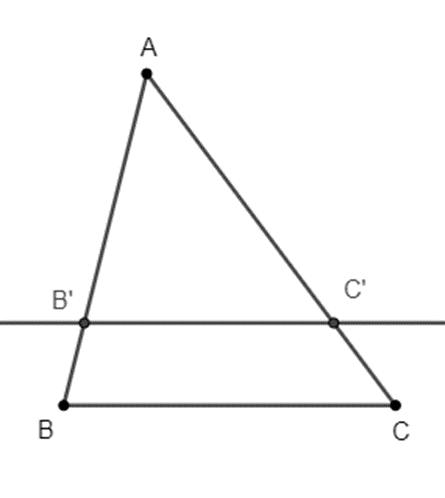
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
|
GT |
\(\Delta ABC\), B’C’ // BC (B’ ∈ AB, C’ ∈ AC). |
|
KL |
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}}\); \(\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}}\); \(\frac{{B'B}}{{AB}} = \frac{{C'C}}{{AC}}\). |
Cho hai tập hợp khác rỗng: A = (m – 1; 4], B = (−2; 2m + 2), với m ∈ ℝ. Xác định m để:
a) A ∩ B = Ø;
b) A ⊂ B;
c) B ⊂ A;
d) (A ∩ B) ⊂ (−1; 3).
Cho tam giác ABC có P là trung điểm của AB và hai điểm M, N thỏa các hệ thức: \(\overrightarrow {MB} - 2\overrightarrow {MC} = \overrightarrow 0 \) và \(\overrightarrow {NA} + 2\overrightarrow {NC} = \overrightarrow 0 \). Chứng minh rằng 3 điểm M, N, P thẳng hàng.
Cho hai tập hợp khác rỗng A = (m – 1; 4]; B = (−2; 2m + 2), m ∈ ℝ. Tìm m để A ∩ B ≠ Ø.
Cho x, y, z > 0 thỏa mãn x + y + z = 1. Tìm giá trị lớn nhất của
\(Q = \frac{x}{{x + \sqrt {x + yz} }} + \frac{y}{{y + \sqrt {y + zx} }} + \frac{z}{{z + \sqrt {z + xy} }}\).
Cho hai hàm số y = x2 và y = mx + 4, với m là tham số. Khi m = 3, tìm tọa độ các giao điểm A, B của hai đồ thị của hai hàm số trên.
Tìm giá trị lớn nhất của biểu thức \(A = 11 - \sqrt {{x^2} + 7x + 4} \).
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:
|
x |
− ∞ 1 2 3 4 + ∞ |
|
f’(x) |
− 0 + 0 − 0 − 0 + |
Hàm số y = 3f(x + 2) – x3 + 3x đồng biến trên khoảng nào dưới đây?
Trong khai triển (x – 2)100 = a0 + a1x1 + … + a100x100. Tổng hệ số
a0 + a1 + a2 + … + a100 bằng:
Người ta muốn xây một cái bể chứa nước dạng khối hộp chữ nhật không nắp có thể tích \(\frac{{500}}{3}\) m3. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500 000 đồng/m3. Nếu biết xác định kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất, chi phí thấp nhất đó là:
Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọc. Có bao nhiêu cách xếp hàng khác nhau nếu ông hay bà An đứng ở đầu hoặc cuối hàng.
Một bó hoa 12 bông gồm: 5 hoa hồng, 4 hoa lan còn lại là hoa cúc. Chọn ngẫu nhiên 5 bông hoa. Tính xác suất sao cho chọn đủ ba loại và số cúc không ít hơn 2.
