Từ một điểm A nằm ngoài đường tròn (O) kẻ hai tiếp tuyến AB AC (B và C là hai tiếp điểm). Kẻ đường kính CD của đường tròn (O).
a) Chứng minh OA ⊥ BC.
b) Chứng minh: BD // OA.
c) Kẻ BH ⊥ CD. Gọi K là giao điểm của BH và AD. Chứng minh K là trung điểm của BH.
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
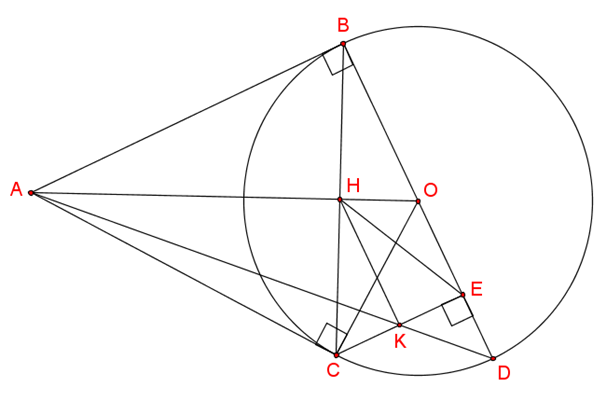
a) Ta có OB = OC (=R).
Suy ra O thuộc đường trung trực của đoạn thẳng CB.
Ta có AB = AC (tính chất hai tiếp tuyến cắt nhau)
Suy ra A thuộc đường trung trực của đoạn thẳng BC.
Như vậy A, O thuộc đường trung trực của BC suy ra AO ⊥ BC (đpcm)
b) Ta có \[\widehat {CBD}\] = 90° (góc nội tiếp chắn nửa đường tròn)
⇒ BD ⊥ BC mà AO ⊥ BC (chứng minh trên)
⇒ BD // AO (đpcm)
c) Ta có KH // AC (vì cùng vuông góc CD).
Theo định lý Ta-let, ta có:
\[\frac{{{\rm{KH}}}}{{{\rm{AC}}}}{\rm{ = }}\frac{{{\rm{DH}}}}{{{\rm{DC}}}} \Rightarrow {\rm{KH = }}\frac{{{\rm{DH}}\,{\rm{.}}\,{\rm{AC}}}}{{{\rm{DC}}}}\] (1)
Xét ΔACO và ΔBHD có: \[\widehat {ACO} = \widehat {BHD} = 90^\circ \]
\[\widehat {ACO} = \widehat {BDO}\] (hai góc đồng vị, BD // AO)
⇒ ∆ACO ᔕ ∆BHD (g.g)
⇒ \[\frac{{AC}}{{BH}} = \frac{{CO}}{{HD}} \Rightarrow BH = \frac{{AC.HD}}{{CO}}\] (2)
Từ (1) và (2) ta có: \[\frac{{KH}}{{BH}} = \frac{{CO}}{{DC}} = \frac{1}{2}\].
Vậy BK = KH, K là trung điểm cạnh BH (đpcm).
Từ một điểm A nằm ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ, vẽ MI vuông góc với AB, MK vuông góc với AC (I thuộc AB, K thuộc AC).
a) Chứng minh AIMK, ABOC là các tứ giác nội tiếp;
b) Vẽ MP vuông góc với BC (P thuộc BC). Chứng minh \(\widehat {MPK} = \widehat {MBC}\);
c) Chứng minh MI.MK = MP2;
d) Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Đường thẳng qua M song song với AB cắt CI tại N.
Chứng minh rằng NG // (SCD).
c) Chứng minh rằng MG // (SCD).
Cho tam giác ABC vuông tại A. Điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC.
a) So sánh độ dài AM, DE.
b) Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất.
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Đường cao AH cắt đường tròn (O) tại D. Kẻ đường kính AE của đường tròn (O). Chứng minh:
a) BC // DE.
b) Tứ giác BCED là hình thang cân.
Cho hàm số bậc nhất y = (2m − 1)x + m − 1 (d)
a) Tìm m để hàm số đồng biến.
b) Tìm m để đường thẳng (d) cắt đường thẳng y = 2x + 1 tại một điểm trên trục tung.
c) Cho m = 2 vẽ đường thẳng (d) và khoảng cách từ gốc tọa dộ đến đường thẳng (d).
Cho tam giác ABC có \(\widehat C = 90^\circ \). Kẻ CH vuông góc với AB. Trên AB và AC lấy tương ứng hai điểm M và N sao cho BM = BC; CN = CH. Chứng minh rằng:
a) MN ^ AC.
b) AC + BC < AB + CH.
Cho hai đường tròn (O; R) và (O; R') tiếp xúc ngoài tại A (R > R'). Vẽ dây AM của đường tròn (O) và dây AN cùa đường tròn (O') sao cho AM ⊥ AN. Gọi BC là một tiếp tuyến chung ngoài của hai dường tròn (O) và (O') với B Î (O), C Î (O').
a) Chứng minh rằng ba đường thẳng MN, BC và OO' đồng quy.
b) Xác định vị trí của điểm M và N để tứ giác MNO'O có diện tích lớn nhất. Tính diện tích lớn nhất đó.
Cho tam giác ABC vuông tại A. Về phía ngoài của tam giác vẽ các hình vuông ABDE, ACGH.
a) Chứng minh tứ giác BCHE là hình thang cân.
b) Vẽ đường cao AK của tam giác ABC. Chứng minh AK, DE, GH đồng quy.