 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
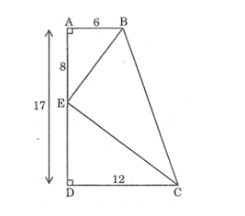
Ta có AD = AE + ED
Suy ra DE = AD – AE
Mà AE = 8 cm, AD = 17cm (giả thiết)
Nên DE = 17 – 8 = 9 (cm)
Ta có \(\frac{{{\rm{AB}}}}{{{\rm{DE}}}} = \frac{6}{9} = \frac{2}{3}\); \(\frac{{{\rm{AE}}}}{{{\rm{DC}}}} = \frac{8}{{12}} = \frac{2}{3}\)
Suy ra \(\frac{{{\rm{AB}}}}{{{\rm{DE}}}} = \frac{{{\rm{AE}}}}{{{\rm{DC}}}}\)
Xét tam giác ABE và tam giác DEC có
\(\frac{{{\rm{AB}}}}{{{\rm{DE}}}} = \frac{{{\rm{AE}}}}{{{\rm{DC}}}}\) (chứng minh trên)
\(\widehat A = \widehat D = 90^\circ \) (giả thiết)
Do đó ∆ABE đồng dạng ∆DEC (c.g.c)
Suy ra \(\widehat {ABE} = \widehat {DEC}\)
Xét tam giác ABE vuông tại A có \(\widehat {ABE} + \widehat {A{\rm{E}}B} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà .\(\widehat {ABE} = \widehat {DEC}\). (chứng minh trên)
Nên \(\widehat {DEC} + \widehat {A{\rm{E}}B} = 90^\circ \)
Lại có \(\widehat {DEC} + \widehat {A{\rm{E}}B} + \widehat {{\rm{CE}}B} = \widehat {A{\rm{ED}}} = 180^\circ \)
Suy ra \(\widehat {BEC} = 90^\circ \)
Vậy \(\widehat {BEC} = 90^\circ \).
Cho đường tròn tâm O, đường kính AB và điểm C thuộc đường tròn sao cho AC > BC. Qua O vẽ đường thẳng vuông góc với dây AC ở H. Kẻ tiếp tuyến tại A của đường tròn cắt tia OH ở D. BD cắt đường tròn tâm O ở E.
a) Chứng minh HA = HC và \(\widehat {DCO} = 90^\circ \)
b) Chứng minh DH . DO = DE . DB
c) Trên tia đối của EA lấy F sao cho E là trung điểm AF. Từ F vẽ đường thẳng vuông góc AD ở K. KF cắt BC ở M. Chứng minh MK = MF.
Cho tam giác ABC vuông tại A. Điểm M thuộc cạnh BC. Từ M vẽ các đường thẳng vuông góc với cạnh AB ở D và với cạnh AC ở E.
a) Chứng minh AM = DE
b) Gọi I là điểm đối xứng của D qua A và K là điểm đối xứng của E qua M. Chứng minh rằng các đoạn thẳng IK, DE, AM đồng quy tại trung điểm O của mỗi đoạn
c) Gọi AH là đường cao của tam giác ABC (H thuộc BC). Tính số đo góc DHE
d) Tìm vị trí của điểm M trên cạnh BC để tứ giác DIEK là hình thoi
Cho hàm số y = (2m – 3).x + m – 5. Tìm m để đồ thị hàm số:
a) tạo với 2 trục tọa độ một tam giác vuông cân
b) cắt đường thẳng y = 3x – 4 tại một điểm trên Oy
c) cắt đường thẳng y = – x – 3 tại một điểm trên Ox.
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a) Chứng minh rằng DE // BF.
b) Tứ giác DEBF là hình gì? Vì sao?
Cho (O; R), lấy điểm A cách O một khoảng bằng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a) Chứng minh: Tam giác OBA vuông tại B và Tam giác OAK cân tại K.
b) Đường thẳng KI cắt AB tại M. Chứng minh rằng KM là tiếp tuyến của đường tròn (O).
c) Tính chu vi tam giác AMK theo R.
Cho hình thang vuông ABCD có \(\widehat A = \widehat D = 90^\circ \), \[AB = AD = \frac{1}{2}CD\]. Gọi E là trung điểm của CD. M là giao điểm của AC và BE, K là giao điểm của AE và DM. Kẻ DH vuông góc với AC, cắt AE ở I.
a) Tứ giác ABCE là hình gì?
b) Tứ giác ABED là hình gì?
c) Tứ giác BIDK là hình gì?
Cho đường tròn (O; R) và điểm A cách O một khoảng 2R. Từ A vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Đường thẳng vuông góc với OB tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.
a) Chứng minh: AMON là hình thoi.
b) Chứng minh: MN là tiếp tuyến của đường tròn.
c) Tính diện tích AMON.
Cho đường tròn (O; R), đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến (d) và (d’) với đường tròn (O). Một đường thẳng qua O cắt đường thẳng d ở M và cắt đường thẳng (d’) ở P. Từ O vẽ một tia vuông góc với MP cắt đường thẳng (d’) ở N.
a) Chứng minh OM = OP và tam giác NMP cân
b) Kẻ OI vuông góc MN. Chứng minh MN là tiếp tuyến của đường tròn (O) tại I
c) Chứng minh AM . BN = R2
d) Tìm vị trí của M để diện tích tứ giác AMNB nhỏ nhất.
Cho đường tròn (O; R) có đường kính AB. Vẽ tiếp tuyến Ax, By của đường tròn(O) lấy một điểm C sao cho AC < BC. Tiếp tuyến tại C của đường tròn (O) cắt Ax, By lần lượt tại E, F.
a) Chứng minh EF= AE + BF.
b) BC cắt Ax tại D. Chứng minh AD2 = DC. DB.
c) Gọi I là giao điểm của OD và AC, OE cắt AC tại H, tia DH cắt AB tại K. Chứng minh IK//AD.
d) IK cắt EO tại M. Chứng minh: A, M, F thẳng hàng.
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh:
a) AB2 = BH . BC;
b) AH2 = BH . HC;
c) AB . AC = AH . BC;
d) AC2 = CH . BC.
Cho hình bình hành ABCD có AB > BC. Đường phân giác của góc D cắt AB tại M, đường phân giác của góc B cắt CD tại N.
a) Chứng minh: AM = CN.
b) Chứng minh: tứ giác DMBN là hình bình hành.