Cho a, b, c > 0 thỏa a2 + b2 + c2 = 3. CMR:
\(\frac{{{a^3}{b^3}}}{c} + \frac{{{b^3}{c^3}}}{a} + \frac{{{a^3}{c^3}}}{b} \ge 3abc\).
Giải bởi Vietjack
Lời giải
BĐT trên tương đương với việc chứng minh
\({a^4}{b^4} + {b^4}{c^4} + {a^4}{c^4} \ge 3{a^2}{b^2}{c^2}\)
Áp dụng BĐT AM - GM ta có:
\({a^4}{b^4} + {b^4}{c^4} \ge 2\sqrt {{a^4}{b^4}.{b^4}{c^4}} = 2{a^2}{b^4}{c^2}\) (1)
\({b^4}{c^4} + {c^4}{a^4} \ge 2\sqrt {{b^4}{c^4}.{c^4}{a^4}} = 2{b^2}{c^4}{a^2}\) (2)
\({c^4}{a^4} + {a^4}{b^4} \ge 2\sqrt {{c^4}{a^4}.{a^4}{b^4}} = 2{c^2}{a^4}{b^2}\) (3)
Cộng vế theo vế của (1), (2), (3) nên ta có:
\(2\left( {{a^4}{b^4} + {b^4}{c^4} + {a^4}{c^4}} \right) \ge 2\left( {{a^2}{b^4}{c^2} + {b^2}{c^4}{a^2} + {c^2}{a^4}{b^2}} \right)\)
\( \Leftrightarrow {a^4}{b^4} + {b^4}{c^4} + {a^4}{c^4} \ge {a^2}{b^4}{c^2} + {b^2}{c^4}{a^2} + {c^2}{a^4}{b^2}\)
\[ \Leftrightarrow {a^4}{b^4} + {b^4}{c^4} + {a^4}{c^4} \ge {a^2}{b^2}{c^2}\left( {{a^2} + {b^2} + {c^2}} \right) = 3{a^2}{b^2}{c^2}\] (*)
Chia 2 vế của (*) với abc > 0 ta suy ra:
\(\frac{{{a^3}{b^3}}}{c} + \frac{{{b^3}{c^3}}}{a} + \frac{{{a^3}{c^3}}}{b} \ge 3abc\) (đpcm).
Dấu “=” xảy ra khi a = b = c = 1.
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng OA vuông góc với BC.
b) Vẽ đường kính CD. Chứng minh rằng BD // AO.
c) Tính độ dài các cạnh của tam giác ABC, biết OB = 2 cm; OA = 4 cm.
d) Đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là M.
Chứng minh: AM.AD = AH.AO.
e) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại E. Chứng minh ED là tiếp tuyến của đường tròn (O).
Cho điểm A nằm ngoài đường tròn (O; R). Vẽ 2 tiếp tuyến AB, AC với đường tròn (O), (B, C là các tiếp điểm). Vẽ đường kính CD của đường tròn (O).
a) Chứng minh rằng: OA ^ BC và OA // BD.
b) Gọi E là giao điểm của AD và đường tròn (O) (E khác D), H là giao điểm của OA và BC. Chứng minh rằng: AE.AD = AH.AO.
Cho đường tròn (O; R) và một điểm A sao cho OA = 2R, vẽ các tiếp tuyến AB, AC với (O; R), B và C là các tiếp điểm. Vẽ đường kính BOD.
a) Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn.
b) Chứng minh rằng: DC // OA.
c) Đường trung trực của BD cắt AC và CD lần lượt tại S và E. Chứng minh rằng OCEA là hình thang cân.
d) Gọi I là giao điểm của đoạn OA và (O), K là giao điểm của tia SI và AB. Tính theo R diện tích tứ giác AKOS.
Cho hàm số bậc nhất y = (m − 1)x + 4 có đồ thị là đường thẳng (d) (m là tham số và m ≠ 1).
a) Vẽ đồ thị khi m = 2.
b) Với giá trị nào của m thì đường thẳng (d) song song với đường thẳng y = −3x + 2 (d1).
c) Tìm m để đường thẳng (d) cắt trục Ox, Oy lần lượt tại hai điểm A, B sao cho diện tích tam giác OAB bằng 2.
Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm.
a) Tính BC, BH, HC, AH .
b) Kẻ phân giác AD. Tính BD, DC.
c) Tính diên tích tam giác AHD.
Cho nửa đường tròn (O), đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K, B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP // KM. Gọi Q là giao điểm của các đường thẳng AP và BM; E là giao điểm của PB và AM.
a) Chứng minh rằng tứ giác PQME nội tiếp đường tròn.
b) Chứng minh: ∆AKN = ∆BKM.
c) Chứng minh: AM . BE = AN . AQ.
d) Gọi R, S lần lượt là giao điểm thứ hai của QA, QB với đường tròn ngoại tiếp ∆OMP. Chứng minh rằng khi M di động trên cung KB thì trung điểm I của RS luôn nằm trên một đường cố định
Cho hàm số bậc bốn f (x) có bảng biến thiên như sau:
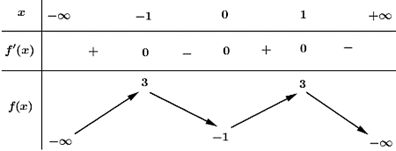
Số điểm cực trị của hàm số g(x) = x2[f (x − 1)]4 là:
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I (I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC (E khác B và C), AE cắt CD tại F. Chứng minh:
a) BEFI là tứ giác nội tiếp đường tròn.
b) AE . AF = AC2.
c) Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ∆CEF luôn thuộc một đường thẳng cố định.
Cho 2 đường thẳng: \(\left( {{d_1}} \right):\;y = \frac{1}{2}x + 2\) và (d2): y = −x + 2.
Gọi A, B lần lượt là giao điểm của (d1) và (d2) với trục Ox, C là giao điểm của (d1), (d2). Tính chu vi và diện tích của tam giác ABC (đơn vị trên hệ trục tọa độ là cm).
Cho hàm số bậc bốn f (x) có bảng biến thiên như sau:
Số điểm cực trị của hàm số g(x) = x4[f (x − 1)]2 là:
