Cho tam giác ABC. Chứng minh rằng:
a) \(\cot {\rm{A + cot B + cot C}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\).
b) \(m_a^2 + m_b^2 + m_c^2 = \frac{3}{4}\left( {{a^2} + {b^2} + {c^2}} \right)\).
Giải bởi Vietjack
a) Áp dụng định lí côsin ta có: cos A = \(\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Ta có \(S = \frac{1}{2}bc\sin A\), suy ra \(\sin A = \frac{{2{\rm{S}}}}{{bc}}\)
Do đó cot A = \(\frac{{co{\rm{sA}}}}{{\sin {\rm{A}}}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}:\frac{{2{\rm{S}}}}{{bc}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}.\frac{{bc}}{{2{\rm{S}}}} = \frac{{{b^2} + {c^2} - {a^2}}}{{4{\rm{S}}}}\)
Chứng minh tương tự ta có:
\(\cot B = \frac{{{a^2} + {c^2} - {b^2}}}{{4{\rm{S}}}}\); \(\cot C = \frac{{{a^2} + {b^2} - {c^2}}}{{4{\rm{S}}}}\)
Do đó:
\(\cot {\rm{A + cot B + cot C = }}\frac{{{c^2} + {b^2} - {a^2}}}{{4{\rm{S}}}} + \frac{{{a^2} + {c^2} - {b^2}}}{{4{\rm{S}}}} + \frac{{{a^2} + {b^2} - {c^2}}}{{4{\rm{S}}}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\)
Vậy \(\cot {\rm{A + cot B + cot C}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\).
b) Áp dụng công thức độ dài đường trung tuyến ta có:
\(m_a^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4}\), \(m_b^2 = \frac{{{a^2} + {c^2}}}{2} - \frac{{{b^2}}}{4}\) và \(m_c^2 = \frac{{{a^2} + {b^2}}}{2} - \frac{{{c^2}}}{4}\)
Suy ra:
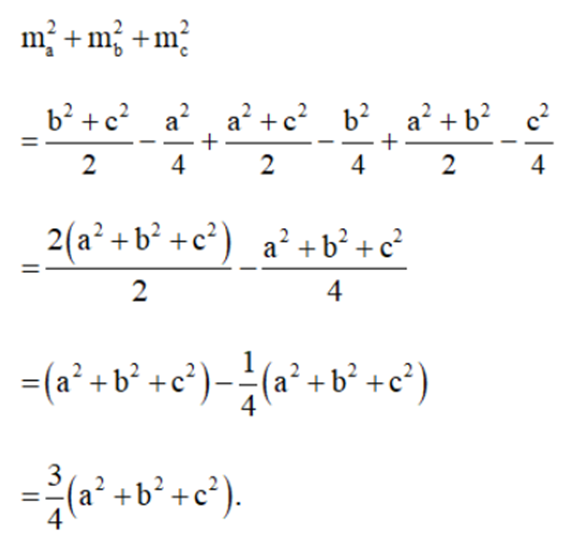
Vậy \(m_a^2 + m_b^2 + m_c^2 = \frac{3}{4}\left( {{a^2} + {b^2} + {c^2}} \right)\).
Cho tam giác ABC. Chứng minh rằng:
a) \(\cot {\rm{A}} = \frac{{{b^2} + {c^2} - {a^2}}}{{4{\rm{S}}}}\).
b) \(\cot {\rm{A + cot B + cot C}} = \frac{{{a^2} + {b^2} + {c^2}}}{{4{\rm{S}}}}\).
Ông Tư mua một khu đất hình chữ nhật dài 48m, rộng 25m. Ông thuê rào xung quanh bằng lưới giá 2 500 đồng/dm. Hỏi ông tốn tất cả bao nhiêu tiền, biết lúc rào ông có chừa lối đi rộng 2m.
Hai kho gạo có 155 tấn gạo. Nếu thêm vào kho thứ nhất 8 tấn và thêm vào kho thứ hai 17 tấn thì số gạo ở mỗi kho bằng nhau. Hỏi lúc đầu mỗi kho có bao nhiêu tấn gạo?
Cho biết log25 7 = a và log2 5 = b. Tính \({\log _{\sqrt[3]{5}}}\frac{{49}}{8}\) theo a, b.
Trên mặt phẳng tọa độ Oxy cho hai điểm A(1; 2) và B(3; 4)
a) Tìm hệ số a của đường thẳng đi qua A và B.
b) Xác định hàm số biết đồ thị của nó là đường thẳng đi qua A và B.
Cho tam giác ABC vuông tại đỉnh A, đường cao AH, từ H kẻ HM vuông góc AC và trên HM lấy điểm E sao cho MH = EM. Kẻ HN vuông góc AB và trên HN lấy điểm D sao cho NH = DN.
a) Chứng minh D, A, E thẳng hàng.
b) Chứng minh MN song song DE.
c) Chứng minh BD song song CE.
d) Chứng minh AD = AE = AH, suy ra tam giác DHE vuông.
Có bao nhiêu số tự nhiên thỏa mãn\(\frac{{A_{n + 4}^4}}{{\left( {n + 2} \right)!}} < \frac{{15}}{{\left( {n - 1} \right)!}}\)
Cho tứ diện ABCD trong đó góc giữa hai đường thẳng AB và CD bằng α. Gọi M là điểm bất kì thuộc cạnh AC, đặt AM = x (0 < x < AC). Xét mặt phẳng (P) đi qua điểm M và song song với AB, CD.
a) Xác định vị trí điểm M để diện tích thiết diện của hình tứ diện ABCD khi cắt bởi mp (P) đạt giá trị lớn nhất.
b) Chứng minh rằng chu vi thiết diện nêu trên không phụ thuộc vào x khi và chỉ khi AB = CD.
Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DE. Gọi I, J lần lượt là trung điểm MP, NQ. Chứng minh IJ // AE và \(IJ = \frac{1}{4}AE\).
Cho hình bình hành ABCD có tâm O. Xác định các vectơ sau đây:
a) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {O{\rm{D}}} \);
b) \(\overrightarrow {OA} + \overrightarrow {BO} + \overrightarrow {CO} + \overrightarrow {{\rm{DO}}} \);
c) \(\overrightarrow {AC} + \overrightarrow {BD} + \overrightarrow {BA} + \overrightarrow {{\rm{DA}}} \);
d) \(\overrightarrow {OA} + \overrightarrow {CB} + \overrightarrow {OC} + \overrightarrow {{\rm{AD}}} \).
Nhà máy A sản xuất một loại áo giá vốn là 500 000 000 đồng và giá bán mỗi chiếc sẽ là 400 000 đồng khi đó gọi y (đồng) là số tiền lời (hoặc lỗ) của nhà máy thu được khi bán x cái áo.
Cho tam giác ABC có các đường cao bằng 12 cm, 15 cm, 20 cm. Chứng minh tam giác ABC là tam giác vuông.
