 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Đặt \(A = \frac{{x + 5}}{{x + 2}}\)
Ta có \(A = \frac{{x + 5}}{{x + 2}} = \frac{{x + 2 + 3}}{{x + 2}} = 1 + \frac{3}{{x + 2}}\)
Với x nguyên, để A nguyên thì \(\frac{3}{{x + 2}}\) nguyên
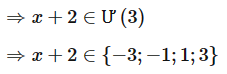
Suy ra x ∈ {– 5; – 3; – 1; 1}
Vậy x ∈ {– 5; – 3; – 1; 1}.
Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.
a) Chứng minh tam giác COD vuông tại O.
b) Chứng minh AC . BD = R2.
c) Kẻ MH vuông góc AB (H ∈ AB). Chứng minh rằng BC đi qua trung điểm của đoạn MH.
Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O; R). Vẽ AH vuông góc với BC. Từ H vẽ HM vuông góc với AB và HN vuông góc với AC (H ∈ BC, M ∈ AB, N ∈ AC). Vẽ đường kính AE cắt MN tại I, tia MN cắt đường tròn (O; R) tại K
a) Chứng minh tứ giác AMHN nội tiếp.
b) Chứng minh AE vuông góc với MN.
c) Chứng minh AH = AK.
Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E.
a) Chứng minh rằng chu vi tam giác ADE bằng 2AB.
b) \(\widehat {DOE} = \frac{1}{2}\widehat {BOC}\).
Cho nửa đường tròn (O; R) đường kính AB. Trên đoạn OB lấy điểm H sao cho HB = 2HO. Đường thẳng vuông góc với AB tại H cắt nửa (O) tại D. Vẽ đường tròn (S) đường kính AO cắt AD tại C.
a) Chứng minh C là trung điểm của AD.
b) Chứng minh 4 điểm C, D, H, O cùng thuộc một đường tròn.
c) CB cắt DO tại E. Chứng minh BC là tiếp tuyến của (S).
d) Tính diện tích tam giác AEB theo R.
Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.
a) Tứ giác OCAB là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.
Cho hình bình hành ABCD tâm O. Gọi M là 1 điểm bất kỳ. Chứng minh
a) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {M{\rm{D}}} = 4\overrightarrow {MO} \)
b) \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{\rm{D}}} = 2\overrightarrow {AC} \).
Cho hàm số y = 2x + 3.
a) Vẽ đồ thị hàm số trên.
b) Gọi A, B là giao điểm của đồ thị với các trục tọa độ. Tính diện tích tam giác OAB (O là gốc tọa độ và đơn vị trên các trục tọa độ là cm).
c) Tính góc tạo bởi đường thẳng y = ax + b và trục Ox.
Chứng minh rằng với mọi giá trị của m:
a) Phương trình: mx2 – (3m + 2)x + 1 = 0 luôn có nghiệm.
b) Phương trình: \(({m^2} + 5){x^2} - \left( {\sqrt 3 m - 2} \right)x + 1 = 0\) luôn vô nghiệm.
Cho 2 hàm số bậc nhất: y = mx + 3 và y = (2m + 1)x – 5. Tìm giá trị m để đồ thị của hai hàm số đã cho là:
a) hai đường thẳng song song.
b) hai đường thẳng cắt nhau.