Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE < BC.
Giải bởi Vietjack
Lời giải
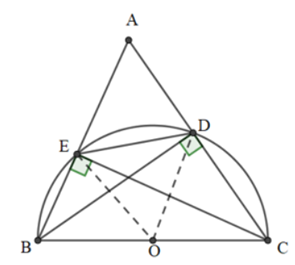
a) Gọi O là trung điểm của BC
\( \Rightarrow OB = OC = \frac{1}{2}BC\) (1)
Xét tam giác DBC vuông tại D (do DB là đường cao của tam giác ABC)
Có DO là đường trung tuyến ứng với cạnh huyền BC
\( \Rightarrow OD = \frac{1}{2}BC\) (2) (tính chất đường trung tuyến ứng với cạnh huyền)
Từ (1) và (2) suy ra \(OB = OC = OD = \frac{1}{2}BC\).
Do đó, ba điểm B, C, D cùng nằm trên đường tròn tâm O bán kính OB.
Xét tam giác BEC vuông tại E (do CE là đường cao của tam giác ABC)
Có EO là đường trung tuyến ứng với cạnh huyền BC
\(OE = \frac{1}{2}BC\) (3) (tính chất đường trung tuyến ứng với cạnh huyền)
Từ (1) và (3) suy ra \(OB = OC = OE = \frac{1}{2}BC\).
Do đó, ba điểm B, C, E cùng nằm trên đường tròn tâm O bán kính OB.
Do đó, bốn điểm B, C, E, D cùng nằm trên một đường tròn tâm O bán kính OB.
b) Xét đường tròn tâm O bán kính OB có đường kính BC.
Ta có DE là một dây cung không đi qua tâm O nên BC > DE do trong một đường tròn dây cung lớn nhất là đường kính.
Cho hình chữ nhật ABCD, O là giao điểm hai đường chéo. M thuộc CD và N thuộc AB sao cho DM = BN.
a) Chứng minh ANCM là hình bình hành, từ đó suy ra các điểm M, O, N thẳng hàng.
b) Qua M kẻ đuờng thẳng song song với AC cắt AD ở E, qua N kẻ đường thẳng song song với AC cắt BC ở F. Chứng minh tứ giác ENFM là hình bình hành.
c) Tìm vị trí của điểm M, N để ANCM là hình thoi.
d) BD cắt NF tại I. Chứng minh I là trung điểm của NF
Cho tam giác ABC nhọn (AB > AC), có \(\widehat B = 45^\circ \) và vẽ đường cao AH. Gọi M là trung điểm của AB. P là điểm đối xứng với H qua M.
a) Chứng minh rằng tứ giác AHBP là hình vuông.
b) Vẽ đường cao BK của tam giác ABC. Chứng minh rằng HP = 2MK.
c) Gọi D là giao điểm của AH và BK. Qua D và C vẽ các đường thẳng song song với BC và AH sao cho chúng cắt nhau tại Q. Chứng minh: ba điểm P, K, Q thẳng hàng.
d) Chứng minh các đường thẳng CD, AB và PQ đồng quy.
