Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của BC, CD và I là giao điểm của AN, DM. Chứng minh rằng: AN ⊥ DM.
Giải bởi Vietjack
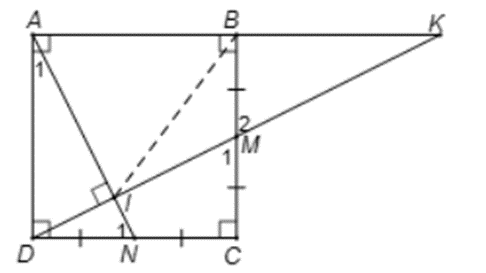
Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:
\(\left\{ \begin{array}{l}AD = DC,\,\,\widehat D = \widehat C\\DN = CM\end{array} \right.\)
Do đó ∆AND = ∆DCM (c.g.c)
Suy ra \({\widehat A_1} = {\widehat D_1}\) (hai góc tương ứng).
Vì ∆ADN vuông ở D, nên \({\widehat A_1} + {\widehat N_1} = 90^\circ \).
Thay \(\widehat {{A_1}} = \widehat {{D_1}}\) vào đẳng thức (1) ta được \(\widehat {{D_1}} + \widehat {{N_1}} = 90^\circ \).
Điều này chứng tỏ tam giác DIN vuông ở I hay AN ⊥ DM.
Cho hình vuông ABCD. Trên tia đối của tia CB lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM = DN. Vẽ hình bình hành MANF, gọi O là trung điểm của AF. Chứng minh rằng:
Tứ giác MANF là hình vuông.
Tìm m để 2 đường thẳng (d) cắt nhau tại 1 điểm trên trục tung cho hàm số y = (m + 2)x + 2m2 + 1 tìm m để hai đường thẳng (d): y = (m + 2)x + 2m2 + 1 và (d'): y = 3x + 3 cắt nhau tại 1 điểm trên trục tung.
Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chứng mình rằng:
a) \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \);
b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} \);
c) \(\overrightarrow {GH} + 2\overrightarrow {GO} = 0\).
Một người bán một chiếc quạt điện với giá 198 000 đồng thì được lãi 10% tiền vốn một chiếc. Hỏi để lãi 10% giá bán thì người đó phải bán chiếc quạt đó với giá bao nhiêu?
Người ta trồng mía trên một khu đất hình chữ nhật có chiều rộng 130m, chiều dài hơn chiều rộng 70 m. Biết rằng, trung bình cứ 100 \({m^2}\) thu hoạch được 300kg mía. Hỏi khu đất đó thu hoạch được bao nhiêu kg mía?
Có tất cả 18 quả táo, cam và xoài. Số quả cam bằng \(\frac{1}{2}\) số quả táo. Số quả xoài gấp 3 lần số quả cam. Tính số quả táo.
Cả ba con gà, vịt, ngỗng cân nặng 10,5 kg. Biết con gà cân nặng 1,5 kg, vịt nặng hơn gà 0,9 kg. Hỏi con ngỗng cân nặng bao nhiêu ki-lô-gam?
Một mảnh đất hình chữ nhật có nửa chu vi là 194 m chiều dài gấp 3 lần chiều rộng. Trên mảnh đất đó, người ta dành phần đất hình vuông cạnh 16,5 m để làm nhà.
a) Tính diện tích mảnh đất đó?
b) Tính diện tích cách làm nhà?
Một hình chữ nhật có nửa chu vi là 26 cm, chiều rộng kém chiều dài 8 cm. Tính diện tích của hình chữ nhật đó
Ba kho thóc có tổng số 1 012 tạ thóc. Biết \(\frac{1}{2}\) số thóc kho A bằng \(\frac{3}{7}\) số thóc kho B và bằng \(\frac{5}{9}\) số thóc kho C. Tìm số thóc của mỗi kho.
Cho 43 số nguyên, trong đó tổng của 7 số bất kì là một số nguyên âm. Chứng minh rằng tổng của 43 số đó là số nguyên âm.
