Cho hình thang ABCD (AB < CD), AD cắt BC tại I, AC cắt BD tại O. Gọi M, N lần lượt là trung điểm của AB, DC. Chứng minh rằng I, M, O, N thẳng hàng.
Giải bởi Vietjack
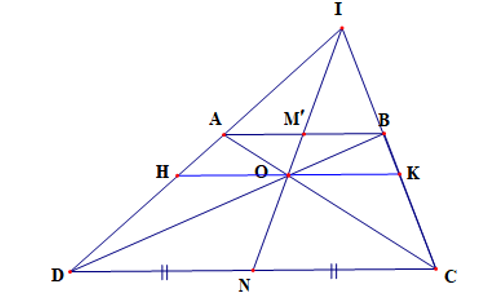
• Gọi M’ là giao điểm của IN và AB. Ta cần chứng minh M’ ≡ M.
Trong DIDN có AM’ // DN nên theo hệ quả định lí Thalès ta có:
Trong DICN có BM’ // CN nên theo hệ quả định lí Thalès ta có:
Suy ra
Mà DN = CN nên AM’ = BM’ hay M’ là trung điểm của AB.
Do đó M’ ≡ M nên I, M, N thẳng hàng (*)
• Qua O kẻ đường thẳng song song với CD cắt ID và IC lần lượt tại H và K.
Trong DADC có HO // DC nên theo hệ quả định lí Thalès ta có: (1)
Trong DBDC có KO // DC nên theo hệ quả định lí Thalès ta có: (2)
Trong DODC có AB // DC nên theo hệ quả định lí Thalès ta có:
Suy ra hay (3)
Từ (1), (2) và (3) suy ra , do đó HO = KO.
Chứng minh tương tự như trên ta có I, O, N thẳng hàng (**)
Từ (*) và (**) ta có I, M, O, N thẳng hàng.
b) Vẽ đường kính BD. Đường thẳng qua O và vuông góc với AD cắt tia BC
tại E. Chứng minh: DC // OA và CD . CO = BA . CE.
Xác định hàm số bậc nhất y = ax + b (a ≠ 0) biết rằng đồ thị của hàm số này song song với đường thẳng y = 2x + 3 và cắt trục hoành tại điểm có hoành độ là –2.
Cho tam giác ABC nhọn có góc , đường cao AH. Điểm D đối xứng với H qua AB. Điểm E đối xứng với H qua AC. Điểm K là giao điểm của DB và EC.
a) ADKE là hình gì ?
Một vòi chảy vào bể trung bình mỗi phút chảy được 27,5 lít nước. Hỏi trong giờ vòi đó chảy được bao nhiêu lít nước?
Có 10 người, để làm xong một công việc thì phải mất 8 ngày. Nếu muốn làm xong cong việc đó trong 5 ngày thì cần phải có bao nhiêu người, biết năng suất lao động của mỗi người là như nhau?
Lớp 5A, 5B, 5C trồng cây. Biết trung bình cộng số cây của ba lớp là 220 cây và nếu lớp 5A trồng bớt đi 30 cây, lớp 5B trồng thêm 80 cây, lớp 5C trồng thêm 40 cây thì số cây 3 lớp trồng bằng nhau. Tính số cây mỗi lớp đã trồng.
Từ 1 điểm A nằm ngoài đường tròn (O; R), kẻ 2 tiếp tuyến AB, AC
với (O; R) (B và C là 2 tiếp điểm).
a) Chứng minh 4 điểm A, B, O, C cùng thuộc 1 đường tròn và AO ⊥ BC tại H.
Một số nếu tăng lên 3 lần rồi bớt đi 14,6 thì được kết quả là 30,4. Số đó là
Kết quả điều tra ở một lớp học cho thấy: Có 20 học sinh thích bóng đá, 17 học sinh thích bơi, 36 học sinh thích bóng chuyền, 14 học sinh thích đá bóng và bơi, 13 học sinh thích bơi và bóng chuyền, 15 học sinh thích bóng đá và bóng chuyền, 10 học sinh thích cả ba môn, 12 học sinh không thích môn nào. Tính xem lớp học đó có bao nhiêu học sinh?
Số học sinh khối 6 của trường khi xếp thành 12 hàng, 15 hàng, 18 hàng đều dư ra 9 học sinh. Hỏi số học sinh khối 6 trường đó là bao nhiêu? Biết rằng số đó lớn hơn 300 và nhỏ hơn 400.
