Cho hình thang vuông ABCD tại A và D. Gọi E, F lần lượt là trung điểm của AD, BC. Chứng minh:
a) ∆AFD cân tại F.
b) \(\widehat {BAF} = \widehat {CDF}\).
 Giải bởi Vietjack
Giải bởi Vietjack
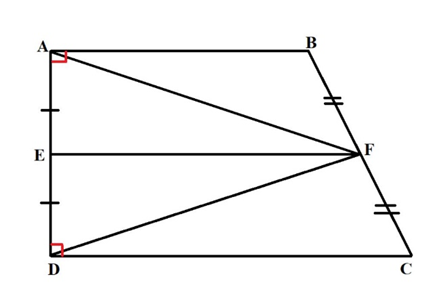
a) Ta có EF là đường trung bình của hình thang ABCD
⇒ EF // AB
Suy ra EF ⊥ AD.
Khi đó EF vừa là trung tuyến vừa là đường cao của tam giác AFD (đpcm)
Vậy tam giác AFD cân tại F.
b) Tam giác AFD cân tại F nên \(\widehat {EAF} = \widehat {EDF}\).
Suy ra \(\widehat {FAB} = \widehat {CDF}\).
8 người đóng xong 500 viên gạch mất 4 giờ. Hỏi 16 người đóng xong 1000 viên gạch trong bao lâu (biết năng suất mỗi người đều như nhau)
Một lớp học có 40 học sinh trong đó có 30 học sinh giỏi toán, 25 học sinh giỏi giỏi tiếng việt, 2 học sinh không giỏi môn nào. Hỏi lớp đó có bao nhiêu học sinh giỏi cả toán và tiếng việt?
Rút gọn biểu thức sau:
B = 2100 – 299 + 298 – 297 + … – 23 + 22 – 2 + 1Cứ 1 tạ hạt tươi đem phơi khô thì khối lượng hạt đó giảm đi 15 kg. Hỏi có 200 kg hạt tươi đó đem đem phơi khô thì được bao nhiêu ki-lô-gam hạt khô?
Cho (O; R) và 3 dây AB, AC, AD; gọi M và N là lần lượt là hình chiếu của B trên các đường thẳng AC, AD. Chứng minh MN ≤ 2R
Cho dãy số: 1; 1; 2; 4; 7; 13; 24; . . .
Tìm số hạng thứ 10 của dãy số.
7 người làm xong 5 công việc phải hết 50 ngày. Hỏi 10 người muốn làm xong 10 công việc như thế thì phải cần bao nhiêu ngày? (mức làm của mỗi người như nhau).
Một con dốc có góc nghiêng 30° so với mặt đất, đỉnh dốc có độ cao 500 m. Một người di chuyển xuống từ đỉnh con dốc một khoảng 150 m thì người ở độ cao bao nhiêu so với mặt đất ?
Tìm hai số biết rằng tổng của chúng gấp 5 lần hiệu của chúng và tích của chúng gấp 4 008 lần hiệu của chúng.