Cho phân số . Hãy tìm một số sao cho khi đem tử số và mẫu số của phân số đã cho cộng với số đó ta được phân số tối giản .
 Giải bởi Vietjack
Giải bởi Vietjack
Nếu đem tử số và mẫu số của phân số đã cho cộng với số đó thì hiệu không đổi
Hiệu của tử số và mẫu số ban đầu là: 99 – 29 = 70
Ta có sơ đồ sau:
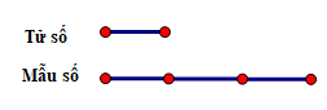
Tử số mới là:
70 : (3 – 1) = 35
Số đó là:
35 – 29 = 6
Vậy số cần tìm là 6.
Cho tam giác ABC. Trên tia đối của tia AB lấy D sao cho AD = AB, trên tia đối của tia AC lấy điểm E sao cho AE = AC
a) Chứng minh rằng: BE = CD.
Tìm một số tự nhiên có hai chữ số, biết rằng nếu ta viết thêm vào bên trái số đó một chữ số 2 thì ta được số mới mà tổng số đã cho và số mới bằng 346.
b) Đường thẳng AO cắt đường tròn (O) tại P và N (N nằm giữa A và P). Chứng minh AN.AP = AB2.
Cho đường tròn (O; R). Từ A nằm ngoài đường tròn kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh bốn điểm A, B, C, O thuộc cùng một đường tròn.
Trong đợt khảo sát chất lượng, lớp 10C có 11 học sinh đạt điểm giỏi môn Toán, 8 học sinh đạt điểm giỏi môn Lý, 5 học sinh đạt điểm giỏi cả môn Toán và Lý, 4 học sinh đạt điểm giỏi cả môn Toán và Hóa, 2 học sinh đạt điểm giỏi cả môn Hóa và Lý, 1 học sinh đạt điểm giỏi cả ba môn Toán, Lý, Hóa. Hỏi lớp 10C có bao nhiêu học sinh đạt điểm giỏi môn Hóa, biết trong lớp có 16 học sinh giỏi ít nhất một môn?
Một người đi bộ trung bình mỗi phút đi được 73,5 m.
a) Trong giờ người đó đi được bao nhiêu m?
b) Gọi giao điểm của CB và đường tròn (O) là E (E ≠ B). Chứng minh CE . CB = CI . CO.
Một vườn cây hình chữ nhật có diện tích 789,25 m2, chiều dài 38,5 m. Người ta muốn rào xung quanh vườn dài bao nhiêu mét, biết cửa vườn rộng 3,2 m.
Cho tam giác ABC. Trên tia đối của AB lấy D sao cho AD = AC, trên tia đối của AC lấy E sao cho AE = AB. Gọi M và N lần lượt là trung điểm của BE và CD. Chứng minh 3 điểm M, A, N thẳng hàng.
c) Khi A di động trên đường tròn (O; 3R), gọi M là trực tâm tam giác ABC. Chứng minh M di động trên một đường tròn cố định.
Cho đường tròn (O; R), đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax, kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao điểm của CO và AD là I.
a) Chứng minh: CO ⊥ AD.
Tính diện tích một hình tròn, biết nếu giảm đường kính hình tròn đó đi 20% thì diện tích giảm đi 113,04 cm2.