Cho H, K là các giao điểm của đường tròn (O1), (O2). Đường thẳng O1H cắt (O1) tại A, (O2) tại B. O2H cắt (O1) tại C và (O2) tại D. Chứng minh rằng ba đường thẳng AC, BD, HK đồng quy tại 1 điểm.
Giải bởi Vietjack
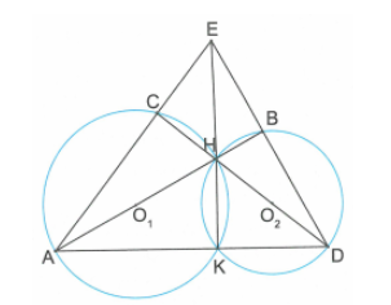
Gọi E là giao điểm của AC và BD.
Vì các tam giác ACH, AKH nội tiếp đường tròn (O1) có cạnh HA là đường kính nên tam giác ACH vuông tại C và tam giác AKH vuông tại K.
Suy ra
Vì các tam giác HDK, HDB nội tiếp đường tròn (O2) có cạnh HD là đường kính nên tam giác HDK vuông tại K và tam giác HBD vuông tại B.
Suy ra
Từ (2), (4), suy ra ba điểm A, K, D thẳng hàng.
Do đó HK ⊥ AD.
Từ (1), (3), suy ra H là trực tâm của tam giác AED.
Do đó HE ⊥ AD.
Vì vậy H ∈ EK.
Vậy ba đường thẳng AC, BD, HK đồng quy tại 1 điểm.
Số học sinh bốn khối 6, 7, 8, 9 tỉ lệ với các số 9, 8, 7, 6. Biết rằng số học sinh khối 9 ít hơn số học sinh khối 7 là 70 học sinh. Tìm số học sinh mỗi khối.
Số học sinh của một trường là một số tự nhiên có 3 chữ số và lớn hơn 900. Mỗi lần xếp hàng 3, hàng 4, hàng 5 đều không có ai lẻ hàng. Tính số học sinh của trường đó?
Tìm số tự nhiên x, biết: x chia hết cho 4; x chia hết cho 7; x chia hết cho 8 và x nhỏ nhất.
Một hình vuông có chu vi là 1 m 4 cm. Một hình chữ nhật có trung bình cộng độ dài hai cạnh bằng độ dài cạnh hình vuông và có chiều dài gấp 3 lần chiều rộng. Hỏi diện tích nào lớn hơn và lớn hơn bao nhiêu cm2?
Một cửa hàng có 32,8 tạ gạo, ngày thứ nhất cửa hàng bán được số gạo, ngày thứ hai cửa hàng bán được số gạo còn lại. Hỏi cửa hàng còn lại bao nhiêu kg gạo chưa bán?
Một khu rừng hình chữ nhật có chu vi 5 km 60 dam. Chiều dài hơn chiều rộng 800 m.
a) Hỏi diện tích khu rừng đó bằng bao nhiêu ha? Bao nhiêu m2?
Để đánh số các trang của một quyển sách, người ta phải dùng tất cả 900 chữ số. Hỏi quyển sách đó có bao nhiêu trang?
Một quyển sách giảm giá đi 20% giá ban đầu. Vậy giá mới phải tăng bao nhiêu phần trăm để được trở về như giá ban đầu.
Cho A = 5 + 52 + 53 + ... + 5100.
a) Số A là số nguyên tố hay hợp số?
b) Số A có phải là số chính phương không?
