Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trọng tâm tam giác ABD.Mặt bên (SAB) tạo với đáy một góc bằng 60°.Tính theo a khoảng cách từ B đến mặt phẳng (SAD).
Giải bởi Vietjack
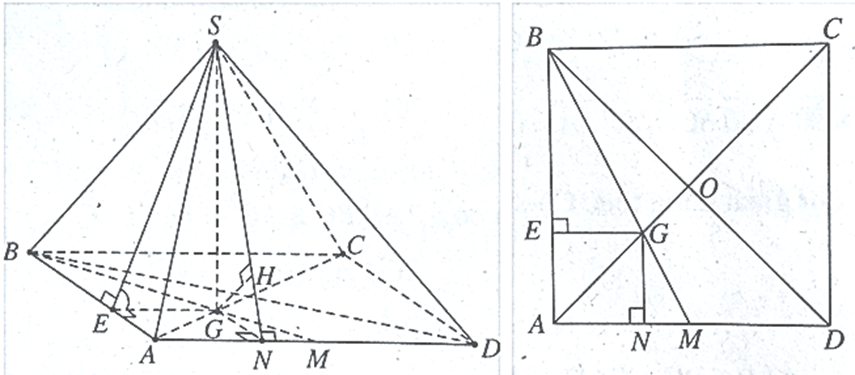
+ Xác định góc của (SAB) và mặt phẳng đáy.
Gọi G là trọng tâm tam giác ABD và E là hình chiếu của G lên AB. Ta có:
AB ^ SG và AB ^ GEÞ AB ^ (SEG) Þ AB ^ SE.
SE ^ AB và GE ^AB\(\left( {\widehat {\left( {SAB} \right)\,,\,\left( {ABCD} \right)}} \right) = \widehat {SEG} = 60^\circ \)
+ Xác định khoảng cách từ B đến mặt phẳng (SAD).
Hạ GN ^ AD. Tương tự như trên, ta có: AD ^ GN và AD ^ SGÞ AD ^ (SGN)
Hạ GH ^ SN, ta có GH ^ (SAD) suy ra khoảng cách từ G đến (SAD) là GH.
+ Tính GH.
Trong tam giác vuông SGN, ta có: \(\frac{1}{{G{H^2}}} = \frac{1}{{G{S^2}}} + \frac{1}{{G{N^2}}}\) (1)
Do GN // AB nên \(\frac{{GN}}{{BA}} = \frac{{MG}}{{MB}} = \frac{1}{3}\)
Ta có: \[GN = \frac{{BA}}{3} = \frac{a}{3}\]
Trong tam giác SGE, ta được \(GS = GE\,.\,\tan 60^\circ = \frac{{a\sqrt 3 }}{3}\) (Do GE = GN)
Thế vào (1) ta được:
\(\frac{1}{{G{H^2}}} = \frac{1}{{G{S^2}}} + \frac{1}{{G{N^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{a}{3}} \right)}^2}}} = \frac{{36}}{{3{a^2}}}\)
\( \Rightarrow GH = \frac{{a\sqrt 3 }}{6}\)
Ta có: M Î(SAD) và MB= 3MG
\( \Rightarrow d\left( {B,\;\left( {SAD} \right)} \right) = 3d\left( {G,\;\left( {SAD} \right)} \right) = 3\,.\,\frac{{a\sqrt 3 }}{6} = \frac{{a\sqrt 3 }}{2}\).
Tìm m để mọi x Î [0; +∞) đều là nghiệm của bất phương trình:
(m2 − 1)x2 − 8mx + 9 − m2 ≥ 0
Tìm m để bất phương trình f(x) > 0 đúng với mọi x thuộc (0; 1)
Từ điểm I nằm ngoài đường tròn (O), vẽ cát tuyến cắt đường tròn tại A và B (IA < IB).Các tiếp tuyến tại A và B cắt nhau tại M. OM cắt AB tại K.
a) Chứng minh K là trung điểm của AB.
b) Vẽ MH ^ OI tại H. Chứng minh OB2 = OH.OI.
c) Gọi N là giao điểm của AB và MH. Chứng minh IA.IB = IK.IN.
Trong tam giác ABC vuông tại A có \(AC = 3a;\;AB = 3\sqrt 3 a,\;\cot B\) bằng?
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM < MB. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn (O) tại D.
1) Chứng minh: SD là tiếp tuyến của đường tròn (O).
2) Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính độ dài đoạn thẳng AE theo R và r.
3) Cho AM = r. Gọi K là giao điểm của BM và AD. Chứng minh: \(\frac{{M{D^2}}}{6} = KH\,.\,KD\).
Tam giác ABC vuông tại A, AB = a, AC = 3a.Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC.
a) Chứng minh \(\frac{{DE}}{{DB}} = \frac{{DB}}{{DC}}\).
b) Chứng minh tam giác BDE đồng dạng với tam giác CDB.
c) Tính tổng \(\widehat {AEB} + \widehat {BCD}\) bằng hai cách.
Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB.
Tổng của số thứ nhất và số thứ hai là 18,36;tổng của số thứ hai và số thứ ba là 21,64; tổng của số thứ ba và số thứ nhất là 20. Tính tổng của ba số đó?
Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a, diện tích mặt bên ABB’A’ bằng 2a2. Tính thể tích V của khối lăng trụ ABC.A’B’C’
Cho tam giác ABC.Gọi I là điểm trên cạnh BC sao cho 2CI = 3BI. Hãy phân tích \[\overrightarrow {AI} \]qua hai vectơ \[\overrightarrow {AB} \] và \[\overrightarrow {AC} \]
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy C1, A1, B1 sao cho các đường thẳng AA1, BB1, CC1, đồng quy tại O. Đường thẳng qua O // AC cắt A1B1, B1C1, tại K và M tương ứng. CMR: OK = OM
Tìm ba số, biết tổng thứ nhất và thứ hai bằng 182. Tổng của số thứ hai và thứ ba bằng 176, tổng của số thứ ba và số thứ nhất bằng 188.
Cho tam giác ABC. Điểm M là điểm chính giữa cạnh AB. Trên cạnh AC lấy AN bằng \(\frac{1}{2}\) NC. Hai đoạn thẳng BN và CM cắt nhau tại K. Hãy tính diện tích tam giác AKC? Biết diện tích tam giác KAB bằng 42 dm2.
Cho x, y, z là các số thực không âm thỏa mãn x+y+ z = 1. Tìm GTLN của biểu thức:\(P = \sqrt {2{x^2} + x + 1} + \sqrt {2{y^2} + y + 1} + \sqrt {2{z^2} + z + 1} \).
