Trên mặt chiếc đồng hồ, kim giây đang ở vị trí ban đầu chỉ vào số 3 (Hình 1). Kim giây quay ba vòng và một phần tư vòng (tức là \(3\frac{1}{4}\) vòng) đến vị trí cuối chỉ vào số 6. Khi quay như thế, kim giây đã quét một góc với tia đầu chỉ vào số 3, tia cuối chỉ vào số 6.

Góc đó gợi nên khái niệm gì trong toán học? Những góc như thế có tính chất gì?
 Giải bởi Vietjack
Giải bởi Vietjack
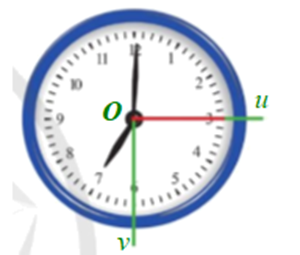
Kim giây đã quét một góc với tia đầu Ou chỉ vào số 3, tia cuối Ov chỉ vào số 6 (hình vẽ trên), góc này là một góc lượng giác.
Những góc lượng giác có cùng tia đầu và tia cuối thì có số đo hơn kém nhau k360° (hay k2π).
Cho góc lượng giác (Ou, Ov) có số đo là \( - \frac{{11\pi }}{4}\), góc lượng giác (Ou, Ow) có số đo là \(\frac{{3\pi }}{4}.\) Tìm số đo của góc lượng giác (Ov, Ow).
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = \frac{{5\pi }}{6}\).
Tính các giá trị lượng giác của mỗi góc sau: 225°; ‒225°; ‒1 035°; \(\frac{{5\pi }}{3};\frac{{19\pi }}{2}; - \frac{{159\pi }}{4}\).
Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác (OA, OM), (OA, ON), (OA, OP) lần lượt bằng \(\frac{\pi }{2};\frac{{7\pi }}{6}; - \frac{\pi }{6}\).
Tính các giá trị lượng giác của góc alpha trong mỗi trường hợp sau:
\(cos\alpha = - \frac{2}{3}\) với \( - \pi < \alpha < 0\)
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác (OA, OM) = α, góc lượng giác (OA, OM’) = – α (Hình 13).
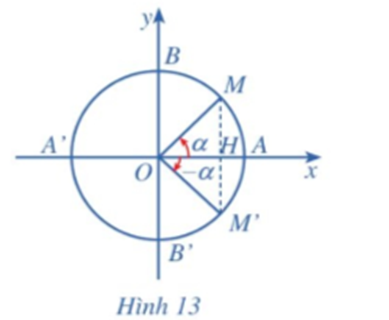
a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.
b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác α và – α.Tính các giá trị lượng giác (nếu có) của mỗi góc sau:
\(\frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
Hãy biểu diễn trên mặt phẳng góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{5\pi }}{4}\).
Cho góc lượng giác alpha. So sánh:
\(1 + {\cot ^2}\alpha \) và \(\frac{1}{{{{\sin }^2}\alpha }}\) với sinα ≠ 0
Tìm các giá trị lượng giác của góc lượng giác \(\alpha = \frac{\pi }{4}\).
Tính các giá trị lượng giác (nếu có) của mỗi góc sau:
kπ (k ∈ ℤ);
Tính các giá trị lượng giác (nếu có) của mỗi góc sau:
\(\frac{\pi }{3} + \left( {2k + 1} \right)\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Một vệ tinh được định vị tại vị trí A trong không gian. Từ vị trí A, vệ tinh bắt đầu chuyển động quanh Trái Đất theo quỹ đạo là đường tròn với tâm là tâm O của Trái Đất, bán kính 9 000 km. Biết rằng vệ tinh chuyển động hết một vòng của quỹ đạo trong 2 h.
Vệ tinh chuyển động được quãng đường 200 000 km sau bao nhiêu giờ (làm tròn kết quả đến hàng đơn vị)?
Cho góc lượng giác α sao cho \(\pi < \alpha < \frac{{3\pi }}{2}\) và \(\sin \alpha = - \frac{4}{5}\). Tìm cosα.