Cho hàm số y = x3 − 3mx2 + 2 có đồ thị (Cm) và đường thẳng Δ: y = −x + 2. Biết (Cm) có hai cực trị và khoảng cách từ điểm cực tiểu của (Cm) đến đường thẳng Δ bằng . Tìm m.
 Giải bởi Vietjack
Giải bởi Vietjack
Xét y’ = 0, ta có:
y’ = 3x2 – 6mx = 3x(x – 2m) = 0
Điều kiện để có hai cực trị là 2m ¹ 0 hay m ¹ 0.
Tọa độ 2 điểm cực trị là: A(0; 2) và B(2m; 2 – 4m3)
Nếu m < 0: A là điểm cực tiểu.
Khi đó d(A; ∆) = 0 ¹ (loại)
Nếu m > 0 thì B là cực tiểu
Khi đó
Do m > 0 nên m = 1.
Vậy m = 1.
Gọi S là tập hợp các số tự nhiên có hai chữ số. Chọn ngẫu nhiên đồng thời hai số từ tập hợp S. Tính xác suất để hai số được chọn có chữ số hàng đơn vị giống nhau.
Cho tam giác ABC vuông cân tại A. Trên các cạnh AB, AC lấy tương ứng hai điểm D, E sao cho AD = AE. Từ A và D kẻ đường vuông góc với BE và cắt BC tại M, N. Tia ND cắt tia CA ở I. Chứng minh A là trung điểm của CI.
Có 40 học sinh giỏi, mỗi em giỏi ít nhất 1 môn. Có 22 em giỏi Văn, 25 em giỏi Toán, 20 em giỏi Anh. Có 8 em giỏi đúng hai môn Văn, Toán. Có 7 em giỏi đúng hai môn Toán, Anh. Có 6 em giỏi đúng hai môn Anh, Văn. Hỏi có bao nhiêu em giỏi cả ba môn Văn, Toán, Anh?
Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi G; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Biểu diễn vecto .
Cho hình vuông ABCD.Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE=CF. Chứng minh tam giác EDF vuông cân.
Một cửa hàng sách hạ giá 10% giá sách nhân ngày Quốc tế thiếu nhi ngày 1/6. Tuy vậy, cửa hàng vẫn còn lãi 8%. Hỏi ngày thường thì cửa hàng được lãi bao nhiêu phần trăm?
Cho parabol (P): y = x2 và hai điểm A(0; 1); B(1; 3). Viết phương trình đường thẳng d song song với AB và tiếp xúc với (P).
Cho hình vuông ABCD.Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE = CF. Gọi I là trung điểm của EF. Chứng minh BI = DI.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a. Gọi M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM).
Cho hàm số y = ax4 + bx2 + c (a ≠ 0) có bảng biến thiên dưới đây:
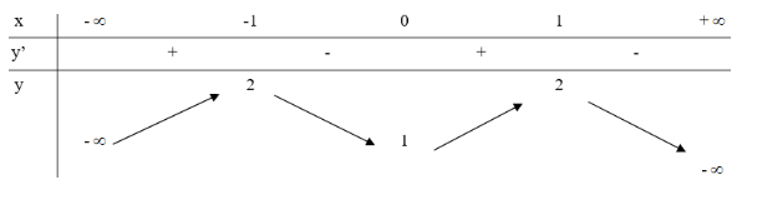
Tính P = a – 2ab + 3c.
Trong kì thi học sinh giỏi tỉnh có 4 bạn Phương, Dương, Hiếu, Hằng tham gia. Được hỏi quê mỗi người ở đâu ta nhận được các câu trả lời sau:
Phương: Dương ở Thăng Long còn tôi ở Quang Trung.
Dương : Tôi cũng ở Quang Trung còn Hiếu ở Thăng Long.
Hiếu : Không, tôi ở Phúc Thành còn Hằng ở Hiệp Hoà.
Hằng : Trong các câu trả lời trên đều có 1 phần đúng 1 phần sai.
Hỏi quê của Dương ở đâu?
Cho hàm số với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên khoảng (2; +∞). Tìm số phần tử của S.
Cho hàm số y = f(x) có đạo hàm f '(x) trên R. Hình vẽ bên là đồ thị của hàm số y = f '(x). Hàm số g(x) = f(x − x2) nghịch biến trên khoảng nào trong các khoảng dưới đây:
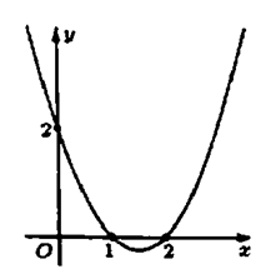
A. ;
B. ;
C. ;
D. .