Cho hình chóp tứ giác đều cạnh đáy bằng a, SB = 2a. Tính thể tích khối cầu ngoại tiếp hình chóp?
Giải bởi Vietjack
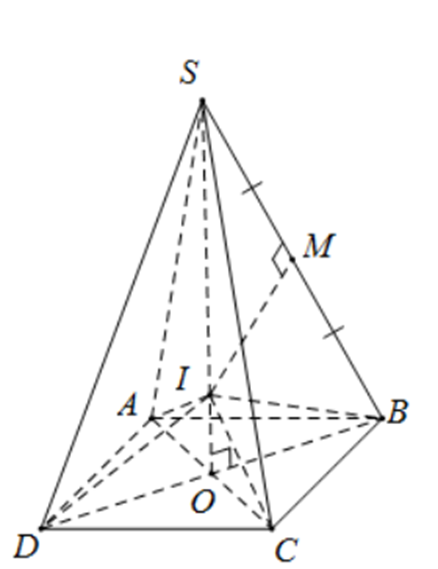
Vì S.ABCD là hình chóp đều nên đường cao SO của hình chóp cũng chính là trục của đa giác đáy
Xét ΔBCD vuông cân tại C có BC = CD = a
⇒ BD = \(\sqrt {B{C^2} + C{D^2}} = a\sqrt 2 \)
⇒ BO = \(\frac{1}{2}BD = \frac{{a\sqrt 2 }}{2}\)
Xét ΔSOB vuông tại O có SB = 2a , BO = \(\frac{{a\sqrt 2 }}{2}\)
⇒ SO = \(\sqrt {S{B^2} - B{O^2}} = \frac{{a\sqrt {14} }}{2}\)
Trong mặt phẳng (SOB), ta vẽ trung trực của SB, đường này cắt SO tại I. Rõ ràng I là tâm mặt cầu ngoại tiếp S.ABCD
Gọi M là trung điểm của SB
⇒ SM = \(\frac{1}{2}SB = a\)
Xét ΔSMI và ΔSOB ta có:
Chung \(\widehat S\)
\(\widehat {SMI} = \widehat {SOB} = 90^\circ \)
⇒ ΔSMI ~ΔSOB (g.g)
⇒ \(\frac{{SI}}{{SB}} = \frac{{SM}}{{SO}}\)
⇒ SI = \(\frac{{SB.SM}}{{SO}} = \frac{{2a.a}}{{\frac{{a\sqrt {14} }}{2}}} = \frac{{2a\sqrt {14} }}{7}\)
Vì SI chính là bán kính mặt cầu ngoại tiếp S.ABCD nên ta có:
Vkhối cầu = \(\frac{4}{3}\)π.SI3 = \(\frac{{64\pi \sqrt {14} }}{{147}}\).
Trong mặt phẳng, cho tam giác ABC có AC = 4 cm, \(\widehat A\)= 60°, \(\widehat B\)= 45°. Độ dài cạnh BC là?
Cho điểm M thuộc đoạn thẳng AB sao cho 2MA = 5MB. Khi đó ta có biểu thức liên hệ giữa vectơ \(\overrightarrow {MA} \)và \(\overrightarrow {AB} \).
Giải bất phương trình thì có được nhân chéo hay không? Ví dụ \(\frac{{a + 1 + \sqrt a }}{{\sqrt a - 1}}\)> 1 nhân chéo được không?
Tìm GTNN của \(\left| {x - 2022} \right| + \left| {2023 - x} \right|\).
Cho hình chóp S .ABC có G là trọng tâm tam giác ABC. Gọi M là điểm trên cạnh SA sao cho MA = 2MS, K là trung điểm BC và D là điểm đối xứng của G qua A.
a) Tìm giao điểm H của SK với (MCD).
b) Tính tỉ số \(\frac{{HK}}{{SK}}\).
Tìm x, y biết (x – 1)2022 + \({\left( {\sqrt {y - 2} } \right)^{2023}} = 0\).
Cho ∆ABC vuông tại A (AB < AC), đường cao AH. Gọi M là trung điểm của BC, D là điểm đối xứng với A qua M. trên tia đối của tia HA lấy điểm E sao cho HE = HA.
a) Chứng minh HM // ED và HM =\(\frac{1}{2}\)DE.
b) Chứng minh ABDC là hình chữ nhật.
c) Gọi P, Q lần lượt là hình chiếu của E lên BD và CD, EP cắt AD tại K. Chứng minh DE = DK.
d) Chứng minh 3 điểm H, P, Q thẳng hàng.
Tính diện tích hình thang có hiệu độ dài của đáy bé và chiều cao bằng 4,5 m, biết \(\frac{2}{3}\) đáy bé bằng \(\frac{3}{4}\) chiều cao, đáy lớn hơn đáy bé 1,2 m.
Hộp thứ nhất có 5 chính phẩm và 3 phế phẩm. Hộp thứ hai có 3 chính phẩm và 2 phế phẩm. Chọn ngẫu nhiên một hộp, rồi từ hộp đó lấy ngẫu nhiên 2 sản phẩm. Tính xác suất lấy được 1 chính phẩm và 1 phế phẩm.
Cho tam giác ABC đều cạnh a. Gọi D là điểm đối xứng của A qua BC. M là một điểm bất kì. Khẳng định nào dưới đây đúng?
A. \(\overrightarrow {MB} .\overrightarrow {MC} = A{M^2} + \overrightarrow {AM} .\overrightarrow {AD} + \frac{{{a^2}}}{2}\).
B. \(\overrightarrow {MB} .\overrightarrow {MC} = A{M^2} - \overrightarrow {AM} .\overrightarrow {AD} + {a^2}\).
C. \(\overrightarrow {MB} .\overrightarrow {MC} = A{M^2} + \overrightarrow {AM} .\overrightarrow {AD} + {a^2}\).
D. \(\overrightarrow {MB} .\overrightarrow {MC} = A{M^2} - \overrightarrow {AM} .\overrightarrow {AD} + \frac{{{a^2}}}{2}\).
Vào tháng 5, giá niêm yết một cái tủ lanh tại một siêu thị điện máy là 10000000 đồng. Đến tháng 6, siêu thị giảm 5% cho mỗi chiếc. Sang tháng 7 siêu thị tiếp tục giảm thêm 10% (so với giá tháng 6). Hỏi giá tháng 7 chênh lệch so với giá niêm yết là bao nhiêu tiền?
Biết F(x) là nguyên hàm của hàm số f(x) = sin2x cosx và F(0) = \(\frac{1}{3}\). Tìm x?
Cho tam giác ABC vuông tại C. Gọi D là trung điểm của AB. Kẻ DM vuông góc với AC (M thuộc AC). Gọi E là điểm đối xứng với D qua BC, DE cắt BC tại N.
a) Chứng minh tứ giác CMDN là hình chữ nhật.
b) Tứ giác BDCE là hình gì? Vì sao?
c) Chứng minh: SABC= 2 SCMDN.
d) Tam giác ABC cần có thêm điều kiện gì để tứ giác ABEC là hình thang cân?
Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại A cắt BC ở I.
a) Chứng minh: \(\frac{{IB}}{{IC}} = \frac{{A{B^2}}}{{A{C^2}}}\).
b) Tính IA, IC bắt rằng AB = 20 cm, AC = 28 cm, BC = 24 cm.
