Cho hình thang vuông ABCD (\(\widehat A\) = \(\widehat D\)= 90°) có \[\widehat {BMC}\]= 90°, với M là trung điểm của AD. Chứng minh: AD là tiếp tuyến của đường tròn bán kính BC.
 Giải bởi Vietjack
Giải bởi Vietjack
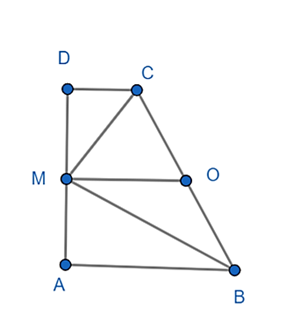
Gọi O là trung điểm BC.
OM là đường trung bình trong hình thang ABCD.
Do đó, OM // AB // DC hay OM ⊥ AD. (1)
Tam giác BMC vuông tại M nên O là tâm đường tròn ngoại tiếp tam giác MBC. (2)
Từ (1) và (2) suy ra AD là tiếp tuyến tại M của đường tròn tâm O.
Vậy AD là tiếp tuyến của đường tròn đường kính BC.
Cho tam giác ABC có AB = 2, AC = 3, \(\widehat A = 60^\circ \). Tính độ dài phân giác góc A?
Cho tam giác ABC có trọng tâm G và hai trung tuyến AM, BN. Biết AM = 15, BN = 12 và tam giác CMN có diện tích là \(15\sqrt 3 \). Tính độ dài đoạn thẳng MN.
Trên cùng phía của đường thẳng xy, vẽ 2 đường thằng AH và BK, sao cho AH vuông góc với xy ở H, BK vuông góc với xy ở K và BK = AH. Gọi O là trung điểm của đoạn HK. Chứng minh: \(\widehat {AOH} = \widehat {BOK}\).
Một người thợ mộc làm những cái bàn và những cái ghế. Mỗi cái bàn khi bán lãi 150 nghìn đồng, mỗi cái ghế khi bán lãi 50 nghìn đồng. Người thợ mộc có thể làm 40 giờ/tuần và tốn 6h làm 1 cái bàn, 3h làm 1 cái ghế. Khách hàng yêu cầu người thợ mộc làm số ghế ít nhất là gấp 3 lần số bàn. Một cái bàn chiếm chỗ bằng 3 cái ghế và ta có phòng để được nhiều nhất 4 cái bàn/tuần. Hỏi người thợ mộc phải sản xuất như nào để có tiền lãi thu về là lớn nhất.
Cho ΔABC vuông tại A. Kẻ BD là tia phân giác của \(\widehat {ABC}\)(D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA.
a) Chứng minh ΔABD = ΔEBD.
b) Chứng minh: DE = AD và DE vuông góc với BC.
c) Chứng minh: BD là đường trung trực của đoạn AE.
d) Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh ba điểm F, D, E thẳng hàng.
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì?
b) Chứng minh rằng CH ⊥ AB.
c) Chứng minh tam giác PIQ cân.
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG.
a) Chứng minh tứ giác BCGE là hình thang cân.
b) Gọi K là giao điểm của các tia DE và FG, M là trung điểm của đoạn thẳng EG. Chứng minh ba điểm K, A, M thẳng hàng.
c) Chứng minh \(\widehat {COD} = 90^\circ \).
d) Chứng minh DC, FB và AM đồng quy.
Cho tam giác ABC vuông tại A (AB < AC) đường cao AH, gọi D là trung điểm của AC lấy E đối xứng H qua D .
a) Chứng minh tứ giác AHCE là hình chữ nhật.
b) Qua A kẻ tia AI // HE cắt đường thẳng BC tại I. Chứng minh tứ giác AEHI là hình bình hành.
c) Trên tia đối của tia HA lấy K sao cho AH = HK. Chứng minh AK là tia phân giác của góc \(\widehat {IAC}\).
d) Tìm điều kiện của tam giác ABC để tứ giác CAIK là hình vuông , khi đó tứ giác AHCE là hình gì ?
Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC.
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp.
2) Chứng minh: BH.BA = BK.BC.
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.
Cho các số 13,1; 13,01; 1,30.103; 1.3.10–3. Có mấy số có ba chữ số có nghĩa?
Từ điểm I nằm ngoài đường tròn (O), vẽ cát tuyến cắt đường tròn tại A và B (IA < IB). Các tiếp tuyến tại A và B cắt nhau tại M. OM cắt AB tại K.
a) Chứng minh K là trung điểm của AB.
b) Vẽ MH ⊥ OI tại H. Chứng minh OB2 = OH.OI.
c) Gọi N là giao điểm của AB và MH. Chứng minh IA.IB = IK.IN.
Một tấm vải dài 105 m . Nếu cắt đi \(\frac{1}{9}\) tấm vải thứ nhất ,\(\frac{3}{7}\) tấm vải thứ hai và \(\frac{1}{3}\) tấm vải thứ ba thì phần còn lại của ba tấm vải bằng nhau. Hỏi mỗi tấm vải dài bao nhiêu mét?
Cho đường tròn (O;R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B. Chứng minh:
a) Tứ giác ABHM nội tiếp.
b) OA.OB = OH.OM = R2.
c) Tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB và D là điểm đối xứng của M qua I.
a. Chứng minh: AD//BM và tứ giác ADBM là hình thoi.
b. Gọi E là giao điểm AM và DC. Chứng minh: AE = EM.