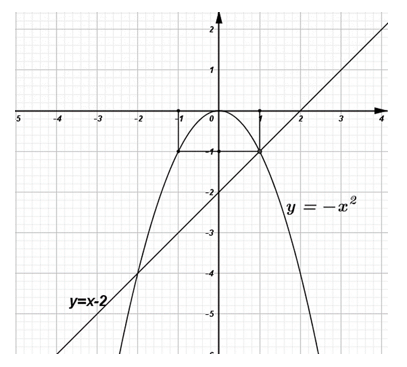
Vẽ đồ thị các hàm số y = –x ² và y = x – 2 trên cùng một hệ trục tọa độ.
Giải bởi Vietjack
y = −x2
Với x = 0 ⇒ y = 0, với x = ±1 ⇒ y = −1
Đồ thị hàm số y = −x² có đỉnh là (0;0) và đi qua 2 điểm (1;−1) và (−1;−1)
y = x − 2
Với x = 0 ⇒ y = −2, với y = 0 ⇒ x = 2
Đồ thị hàm số y = x − 2 đi qua điểm (0;−2) và (2;0)
Đồ thị của hai hàm số như hình vẽ.
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Tìm P là giao điểm của SC và (ADN).
Với các chữ số 0, 2, 3, 5, 6, 7, 9. Lập được bao nhiêu số có 10 chữ số mà trong mỗi số chữ số 5 có mặt đúng 3 lần, chữ số 6 có mặt đúng 2 lần và các chữ số khác, mỗi chữ số có mặt đúng 1 lần?
Một chiếc bút chì có dạng khối lăng trụ lục giác đều có cạnh đáy 3 mm và chiều cao bằng 200 mm. Thân bút chì được làm bằng gỗ và phần lõi được làm bằng than chì. Phần lõi có dạng khối trụ có chiều cao bằng chiều dài của bút và đáy là hình tròn có bán kính 1 mm. Giả định 1 m3 gỗ có giá a triệu đồng, 1 m3 than chì có giá 6a triệu đồng. Tính giá nguyên vật liệu làm một chiếc bút chì như trên.
Cho đường tròn tâm O có đường kính AB và C là một điểm thuộc đường tròn tâm O (C khác A, B). Lấy điểm D thuộc dây cung BC (D khác B, C). Tia AD cắt cung nhỏ BC tại điểm E, tia AC cắt tia BE tại điểm F. Chứng minh tứ giác FCDE nội tiếp.
Cho một đa giác (H) có 60 đỉnh nội tiếp một đường tròn (O). Người ta lập một tứ giác tùy ý có bốn đỉnh là các đỉnh của (H). Tính xác suất để lập được một tứ giác có bốn cạnh đều là đường chéo của (H).
Cho khối lăng trụ ABC.A’B’C’, khoảng cách từ c đến BB′ là , khoảng cách từ A đến BB’ và CC′ lần lượt là 1; 2. Hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm M của B’C’, . Tính thể tích của khối lăng trụ đã cho.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Biết thể tích khối chóp S.ABCD bằng . Gọi α là góc giữa SC và mặt đáy. Tính tan α.
Cho (O) đường kính AB. Lấy C thuộc (O), gọi E là trung điểm BC. Tiếp tuyến tại C của (O) cắt OE ở D. Chứng minh: ΔACB vuông và OE ⊥ BC.
Một túi chứa 6 viên bi trắng và 5 viên bi xanh. Lấy ra 4 viên bi từ túi đó, có bao nhiêu cách lấy được 4 viên bi cùng màu?
Từ các chữ số 0; 1; 2; 3; 4 có thể lập được bao nhiêu số:Có 8 chữ số trong đó chữ số 1có mặt 3 lần, chữ số 4 xuất hiện 2 lần; các chữ số còn lại có mặt đúng một lần.
Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
Cho hình thang ABCD vuông góc tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD. Chứng minh rằng .
Cho hàm số y = ax4 + bx2 + c có đồ thị như hình vẽ bên. Xác định dấu của a, b và c.
