Cho hàm số \[f\left( x \right) = \frac{{x - {m^2} + m}}{{x + 1}}\] với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng ‒2.
 Giải bởi Vietjack
Giải bởi Vietjack
Đạo hàm \[f'\left( x \right) = \frac{{{m^2} - m + 1}}{{{{\left( {x + 1} \right)}^2}}} > 0\], ∀x ∈ [0; 1].
Suy ra hàm số f(x) đồng biến trên [0; 1] \[ \Rightarrow \mathop {\min }\limits_{\left[ {0;1} \right]} f\left( x \right) = f\left( 0 \right) = - {m^2} + m.\]
Theo bài ra:
\[ \Rightarrow \mathop {\min }\limits_{\left[ {0;1} \right]} f\left( x \right) = - 2 \Leftrightarrow - {m^2} + m = - 2 \Leftrightarrow {m^2} - m - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 2\end{array} \right.\]
Cho tam giác ABC có trọng tâm G và hai trung tuyến AM, BN. Biết AM=15, BN = 12 và tam giác CMN có diện tích là \[15\sqrt 3 \]. Tính độ dài đoạn thẳng MN
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = −x4 + 6x2 + mx có ba điểm cực trị?
Người ta dự định xây dựng một tòa tháp 11 tầng tại một ngôi chùa nọ theo cấu trúc, diện tích của mặt sàn tầng trên bằng nửa diện tích mặt sàn tầng dưới, biết diện tích mặt đáy tháp là 15 m2. Yêu cầu là nền tháp lát gạch hoa kích thước 30x30 (cm). Tính số lượng gạch hoa cần mua để lát sàn tháp.
Có hai cơ sở khoan giếng A và B. Cơ sở A giá mét khoan đầu tiên là 8000 (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 500 (đồng) so với giá của mét khoan ngay trước đó. Cơ sở B: Giá của mét khoan đầu tiên là 6000 (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 7% giá của mét khoan ngay trước đó. Một công ty giống cây trồng muốn thuê khoan hai giếng với độ sâu lần lượt là 20 m và 25 m để phục vụ sản xuất. Giả thiết chất lượng và thời gian khoan giếng của hai cơ sở là như nhau. Công ty ấy nên chọn cơ sở nào để tiết kiệm chi phí nhất?
Trong năm đầu tiên đi làm, anh A được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một năm, anh A lại được tăng lương, mỗi tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi khi lĩnh lương, anh A đều phải cất đi phần lương tăng so với năm ngay trước để tiết kiệm mua ô tô. Hỏi sau ít nhất bao nhiêu năm thì anh A mua được ô tô giá 500 triệu, biết rằng anh A được gia đình hỗ trợ 32% giá trị chiếc xe?
Cho tứ giác ABCD gọi M,N là hai điểm di động trên AB,CD sao cho \[\frac{{MA}}{{MB}} = \frac{{ND}}{{NC}}\] và I, J lần lượt là trung điểm của AD, BC.
a, Tính vecto IJ theo vecto AB, DC.
b, Chứng minh trung điểm P của MN nằm trên đường thẳng IJ.
Cho hai đa thức f(x) và g(x) . Xét các tập hợp:
\(A = \left\{ {x \in \mathbb{R}\mid f\left( x \right) = 0} \right\}\)
\(B = \left\{ {x \in \mathbb{R}\mid g\left( x \right) = 0} \right\}\)
\(C = \left\{ {x \in \mathbb{R}\mid \frac{{f\left( x \right)}}{{g\left( x \right)}} = 0} \right\}\)
Trong các mệnh đề sau, mệnh đề nào đúng?
Bác Bình tham gia chương trình bảo hiểm An sinh xã hội của công ty bảo hiểm với thể lệ như sau: Cứ đến tháng 9 hàng năm bác Bình đóng vào công ty 20 triệu đồng với lãi suất hàng năm không đổi \(6{\rm{\% }}/\) năm. Hỏi sau it nhất bao nhiêu năm bác Bình thu về tổng tất cả số tiền lớn hơn 400 triệu đồng?
Hai tiếp tuyến tại A và B của đường tròn (O;R) cắt nhau tại M. Nếu \[MA = R\sqrt 3 \] thì góc góc (AOB) bằng:
Hình vẽ bên là đồ thị của hàm số \[y = \frac{{ax + b}}{{cx + d}}\]
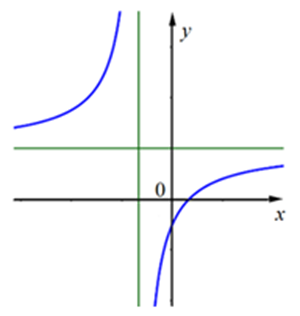
Mệnh đề nào đúng?
Cho hình chóp đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với mặt đáy một góc 60°. Tính thể tích của khối chóp S.ABCD ?
Cho hình vuông ABCD cạnh a. Gọi E là điểm đối xứng của D qua C. Tính \[\overrightarrow {AE} \cdot \overrightarrow {AB} \]
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x3 ‒ 3x2 ‒ 9x + 35 trên đoạn [‒4; 4]. Giá trị của M và m lần lượt là
Có bao nhiêu giá trị nguyên của tham số m để hàm số\[y = \sqrt {5 - m\sin x - \left( {m + 1} \right)\cos x} \] xác định trên ℝ?
Cho hàm số y = f(x) có đồ thị hàm số như hình dưới đây:
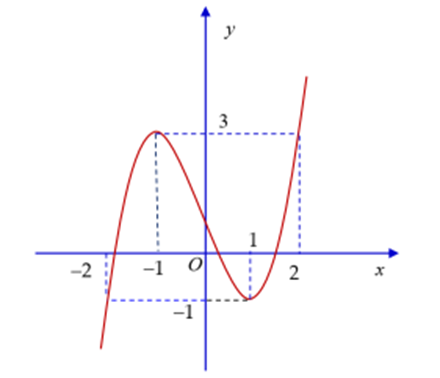
Có tất cả bao nhiêu giá trị nguyên của m để phương trình f(x3 + 3x2 − m) − 3= 0 có nghiệm thuộc đoạn [−1;2]?