Cho 4 điểm A, B, C, D (mỗi bộ 3 điểm không thẳng hàng). Vẽ được bao nhiêu tia mà mỗi tia đều chứa hai trong số các điểm đó?
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
• Chọn điểm A làm gốc, ta vẽ được 3 tia: AB, AC, AD.
• Chọn điểm B làm gốc, ta vẽ được 3 tia: BA, BC, BD.
• Chọn điểm C làm gốc, ta vẽ được 3 tia: CA, CB, CD.
• Chọn điểm D làm gốc, ta vẽ được 3 tia: DA, DB, DC.
Do đó, từ 4 điểm A, B, C, D (mỗi bộ 3 điểm không thẳng hàng), ta vẽ được 12 tia mà mỗi tia đều chứa hai trong số các điểm đó.
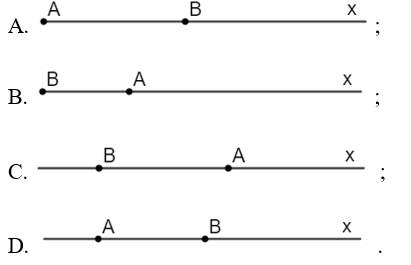
Cho hai tia Ax và AB là hai tia đối nhau. Hình vẽ nào dưới đây biểu diễn đúng?
Chọn cụm từ thích hợp để điền vào chỗ trống.
“Điểm I bất kỳ nằm trên đường thẳng xy là gốc chung của ….”
Cho đường thẳng ab. Lấy điểm I nằm trên đường thẳng ab, trên tia Ia lấy điểm M, trên tia Ib lấy điểm N. Một cặp tia đối nhau gốc I là